Trasformazione triangolo stella – esercizio n. 10 - Digilander

Trasformazione triangolo stella – esercizio n. 10
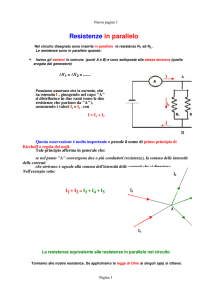
Calcolare la potenza assorbita da ogni resistore presente nel circuito, tensioni e correnti in ogni ramo.
R4
E = 30 V
I=2 A
R1 = 40 Ω
R3
R1
R2 = 25 Ω
R3 = 20 Ω
+
E
R5
R2
I
R 4 = 400 Ω
R5 = 100 Ω
Verrà utilizzata la trasformazione triangolo stella ed il teorema di Millman.
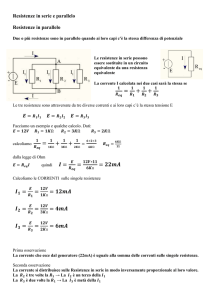
Si stabiliscano i nodi del circuito.
I nodi presenti nel circuito risultano
Per verificare se sia possibile semplificare il essere 4.
circuito occorre stabilirne i nodi e quindi
controllare se vi siano resistenze in serie o Ricerca di resistenze in serie:
in parallelo.
Non sono presenti resistenze in serie.
Eventuale semplificazione del circuito
R4
R1
A
C
R3
B
+
Ricerca di resistenze in parallelo:
Non sono presenti resistenze
parallelo.
E
in
R5
R2
I
D
D
figura n. 1
1
Trasformazione triangolo stella – esercizio n. 10
Si individua il triangolo di resistenze
R1, R3 ed R4 con vertici in A, B, C e si
trasforma in una stella di resistenze
RA, RB ed RC con vertici in A, B e C e
centro stella in O.
Le relazioni necessarie per passare da
resistenze connesse a triangolo a resistenze
connesse a stella sono:
R1 ⋅ R 4
40 ⋅ 400
RA =
=
= 34,78 Ω
R1 + R3 + R 4 40 + 20 + 400
RB =
R3 ⋅ R 4
20 ⋅ 400
=
= 17,39 Ω
R1 + R3 + R 4 40 + 20 + 400
RC =
R1 ⋅ R3
40 ⋅ 20
=
= 1,74 Ω
R1 + R3 + R 4 40 + 20 + 400
O
A
RC
RA
B
RB
C
+
R5
R2
E
I
D
D
figura n. 2
Le resistenze RC ed R2 risultano essere
in serie e pertanto:
RS = RC + R2 = 1,74 + 25 = 26,74 Ω
O
A
RB
RA
+
B
R5
RS
E
I
D
D
figura n. 3
Si trasformi il generatore di corrente in
un generatore di tensione:
E1 = I ⋅ R5 = 2 ⋅ 100 = 200 V
O
A
Facendo ciò le resistenze RB ed R5
saranno in serie e pertanto:
RS1 = RB + R5 = 17,39 + 100 = 117,39 Ω
E
R5
RB
RA
+
B
RS
+
E1
D
D
figura n. 4
2
Trasformazione triangolo stella – esercizio n. 10
Il circuito in oggetto è costituito da soli due nodi e pertanto è possibile applicare il
teorema di Millman per calcolare la d.d.p. VOD:
E
E
30
200
+ 1
+
R A RS1
34,78 117,39
VOD =
=
= 34,37 V
1
1
1
1
1
1
+
+
+
+
R A RS RS1 34,78 26,74 117,39
A
IA
IS1
O
RA
+
RS1
RS
E
+
E1
IS
D
figura n. 5
Si procede al calcolo delle tre correnti IA, IS ed IS1:
Calcolo della corrente IA:
Calcolo della corrente IS1:
VOD = E − RS1 ⋅ IS1
VOD = E + R A ⋅ IA
IA =
VOD − E 34,37 − 30
=
= 0,126
RA
34,78
IS1 =
E1 − VOD 200 − 34,37
=
= 1,41 A
RS1
117,39
Calcolo della corrente IS:
VOD = RS ⋅ IS
IS =
A
Si procede al calcolo della d.d.p. VBD:
VBD = E1 − R5 ⋅ IS1 = 200 − 100 ⋅ 1,41 = 59 V
VOD 34,37
=
= 1,28 A
RS
26,74
IA
O
IS1
E
R5
RB
RA
+
B
RS
+
E1
IS
D
D
figura n. 6
3
Trasformazione triangolo stella – esercizio n. 10
Si ritorna al circuito in cui era presente il
generatore di corrente.
Tale generatore, essendo tra i nodi B e D
sarà sottoposto alla d.d.p. VBD , già
calcolata in precedenza.
VBD = 59 V
Conoscendo VBD è possibile calcolare la
effettiva corrente I5 nella resistenza R5 in
parallelo al generatore di corrente:
VBD = R5 ⋅ I5
A
IA
O
E
B
RB
RA
+
V
59
I5 = BD =
= 0,59 A
R5 100
IS1
R5
RS
I5
I
IS
D
D
figura n. 7
Si calcolino adesso le tre d.d.p. VCA, VBA e VBC:
O
IS1
VCA = R A ⋅ IA − RC ⋅ IS = 34,78 ⋅ 0,126 − 1,74 ⋅ 1,28 = 2,16 V
VBA = R A ⋅ IA + RB ⋅ IS1 = 34,78 ⋅ 0,126 + 17,39 ⋅ 1,41 = 28,90V
VBC = RB ⋅ IS1 + RC ⋅ IS = 17,39 ⋅ 1,41 + 1,74 ⋅ 1,28 = 26,75 V
IA
A
RA
RC
C
RB
B
+
E
R5
R2
IS
I5
I
D
D
figura n. 8
4
Trasformazione triangolo stella – esercizio n. 10
É infine possibile calcolare le correnti I1, I3 ed I4 nelle resistenze R1, R3 ed R4:
VCA = R1 ⋅ I1
⇒
VBC = R3 ⋅ I3
⇒
VBA = R 4 ⋅ I4
⇒
V
2,16
= 0,054 A
I1 = CA =
R1
40
V
26,75
= 1,34 A
I3 = BC =
R3
20
I4 =
VBA 28,90
=
= 0,072 A
R4
400
R4
I4
R1
A
La potenza erogata dal generatore di corrente (corrente I e d.d.p. VBD sono concordi) risulta
essere:
PI = I ⋅ VBD = 2 ⋅ 59 = 118 W
La potenza assorbita dal generatore di tensione (f.e.m. E e corrente IA sono discordi) risulta
essere:
PE = E ⋅ IA = 30 ⋅ 0,126 = 3,78 W
B
I3
I1
+
R5
R2
E
IA
IS
D
Calcolo della potenza erogata dai generatori:
R3
C
Calcolo delle
resistenze;
I
I5
D
figura n. 1
potenze assorbite
dalle
PR1 = R1 ⋅ I12 = 40 ⋅ 0,0542 = 0,12 W
PR2 = R2 ⋅ IS 2 = 25 ⋅ 1,282 = 40,96 W
PR3 = R3 ⋅ I3 2 = 20 ⋅ 1,342 = 35,91 W
PR4 = R 4 ⋅ I42 = 400 ⋅ 0,0722 = 2,07 W
PR5 = R5 ⋅ I5 2 = 100 ⋅ 0,592 = 34,81 W
Verifica potenze erogate ed assorbite:
Perogata = PI = 118 W
Passorbita = PR1 + PR2 + PR3 + PR4 + PR5 + PE = 0,12 + 40,96 + 35,91 + 2,07 + 34,81 + 3,78 = 117,65 ≅ 118 W
5