Molecole biologiche

Molecole biologiche
Macromolecole:
Proteine e Acidi nucleici
catene polimeriche di
aminoacidi e nucleotidi
formate da 103 a 106 atomi, con una massa molecolare compresa tra 103 a 1012 amu (1 amu è circa la massa di un atomo di idrogeno).
Il loro comportamento è determinato da

Solvente (acqua, pH)

Flessibilità (perché sono catene lunghe)

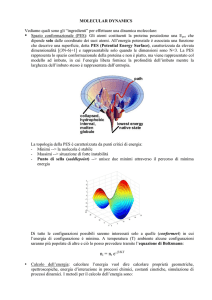
Tempi caratteristici
Scale di tempi e di distanze
•
•
•
•
•
•
Movimenti locali:
fluttuazioni e vibrazioni atomiche
movimenti delle catene laterali
1 ÷ 500 pm
10­15 ÷ 10­1 s
Movimenti di corpo rigido:
movimento delle eliche
100 ÷ 1000 pm
10­9 ÷ 1 s
Movimenti su larga scala:
transizioni elica ­ coil
dissociazione/associazione
folding e unfolding
500 ÷ 50000 pm
10­7 ÷ 104 s!
I polipeptidi: catene molecolari
Un polipeptide (proteina) consiste in una lunga catena di aminoacidi: Proteine: proprietà strutturali
Molecole lineari formate da sequenze di 20 diversi tipi di aminoacidi (Natomi = 40 ÷ 103 e più…).
Gli aminoacidi sono costituiti da un gruppo peptidico e una catena laterale (side chain)
I gradi di libertà rotazionali dei legami peptidici rendono il backbone molto flessibile
I legami peptidici formano il backbone della proteina
Livelli di struttura
Primaria: la specifica sequenza degli aminoacidi
Secondaria: motivi conformazionali locali: α­eliche e β­sheets
Terziaria: la vera struttura 3D
Quaternaria: organizzazione spaziale delle sub­unità molecolari in un complesso proteico
Esempio: triose phosphate isomerase
Rappresentazione all­atom, colorata a seconda del tipo di atomo
Rappresentazione semplificata che descrive il backbone colorato per tipo di struttura secondaria
Superficie esterna accessibile al solvente, colorata a seconda del tipi (acido ­ rosso, basico ­ blu, polare ­ verde, nonpolare – bianco) di residuo
DNA (cenno)
Fino a circa 2 108 paia di nucleotidi (4+1 tipi), ognuno di circa 20 atomi.
Un backbone abbastanza rigido formato da pentosio e fosfato alternati.
Chiralità (⇒ attività ottica) dei legami della catena, che si attorciglia spontaneamente.
Legami a idrogeno tra coppie di polimeri: struttura a doppia elica.
Limiti delle tecniche sperimentali
risoluzione spaziale
misure ad alta risoluzione di strutture molecolari sono possibili solo per sistemi relativamente rigidi
risoluzione energetica
misura delle energie di interazione e deformazione molecolare difficoltosa (i moti lenti di grande ampiezza sono spesso associati a energie piccolissime)
risoluzione temporale
i primissimi eventi dei processi biologici sono veloci, quindi di difficile misurazione
Limiti delle tecniche computazionali
Sistemi biomolecolari troppo complessi per una descrizione che contenga tutta la meccanica quantistica. Si usa invece la meccanica classica con funzioni empiriche per descrivere le interazioni tra gli atomi del un sistema molecolare
Simulazione del comportamento di un sistema molecolare su un computer: anche con queste semplificazioni, solo un numero limitato di atomi (di solito 103÷107 atomi, ≪NA≃6∙1023), per un limitato periodo di tempo (1÷10 ns) può essere simulato. Questo permette di studiare solo sistemi piccoli, per fenomeni veloci (tempi di rilassamento brevi)
Campionatura limitata dello spazio delle conformazioni (un concetto statistico!) di una macromolecola: necessario l'utilizzo dei dati sperimentali per restringersi alla regione interessante
Importanza della complementarietà dell'approccio teorico­
sperimentale!
Complementarità di tecniche
computazionali e sperimentali
L’utilizzo complementare di tecniche di tipo sperimentale e di tipo computazionale è attualmente l’approccio ottimale per lo studio della dinamica delle macromolecole e di molti processi biologici relativi
in particolare gli aspetti strutturali del problema, ovvero lo studio della conformazione, o variazione di conformazione, di una molecola biologica in relazione alla sua attività
Alcune Applicazioni
Conoscere, comprendere, spiegare i meccanismi che portano alla struttura nativa a risoluzione atomica della molecola per comprendere, spiegare, ed eventualmente anche modificare, la sua attività biologica. Alcune applicazioni
Monitorare i cambiamenti strutturali indotti su peptidi o proteine da parte di membrane biologiche
Alcune applicazioni
Effettuare mutazioni puntiformi, che possono fornire indicazioni utili per il riconoscimento del sito attivo o di strutture indispensabili all'attività della molecola o dirette ad una certa funzione.
Alcune Applicazioni
Studiare le conformazionali
variazioni provocate dall’interazione della proteina con uno o più ligandi.
Attivazione o inattivazione di sezione necessaria a compiere la propria funzione biologica
Alcune applicazioni
Applicazioni farmacologiche: viene fornita un’indicazione specifica, o quanto meno restrittiva, della struttura opportuna in funzione del bersaglio del farmaco.
In questo campo, la costruzione di strutture calibrate permette di ridurre la ricerca ad un ristretto raggio d’azione.
Alcune applicazioni
Comprendere il processo di folding delle proteine, ovvero il meccanismo di ripiegamento con cui esse raggiungono la conformazione nativa biologicamente attiva.
Protein folding
A dispetto della loro complessità, la maggior parte delle proteine reali si ripiegano (“foldano”) ad un unico stato nativo mediante un “rapido” e “sicuro” processo di folding
A causa di ciò, in genere si dice che lo stato nativo di una proteina è codificato nella sua sequenza primaria.
Capire come ciò sia possibile è un problema multidisciplinare (coinvolge dati biologici, biochimici, fisici, e richiede tecniche informatiche, statistiche, biotecnologiche) e multiscala (il processo di folding coinvolge movimenti strutturali che coprono scale temporali molto diverse).
Lo stato nativo non è lo stato in cui la proteina nasce!
Obiettivi principali
1) L’analisi e la comprensione dei fenomeni fisici essenziali alla base del folding:
questo potrebbe permettere, in principio, la costruzione, su base chimico­fisica, di efficienti algoritmi per la predizione di strutture
2) La predizione dello stato nativo a partire dalla sequenza degli aminoacidi di una proteina:
protein modeling
Meccanica molecolare (MM)
alias dinamica molecolare (MD)
Le simulazioni MD generano informazioni a livello microscopico (posizioni, velocità degli atomi). Per convertire queste macroscopiche
informazioni (pressione, in energia, osservabili capacità termica, ecc.) c'è bisogno di Termodinamica + Meccanica Statistica
Meccanica molecolare
o dinamica molecolare (MD)
Permette di simulare al computer le strutture ed alcune proprietà dinamiche e termodinamiche dei materiali.
Applicabile solo a molecole/solidi/liquidi nello stato elettronico fondamentale.
Descrive l’evoluzione temporale dei sistemi complessi secondo la legge di Newton:
Fj = mj aj
Inizialmente la MM si applica in vacuo ma oggigiorno è 20
possibile trattare anche gli effetti del solvente.
Altri campi di applicazione della MD
Si può utilizzare per simulare al computer il moto degli atomi e comprendere meccanismi intimi di
•piccole molecole, sia organiche che inorganiche
•reazioni chimiche
•transizioni di fase
•solidi ad altissime pressioni, fratture
•liquidi e miscugli di liquidi (es. liquidi ionici)
•liquidi in geometrie confinate
•lubrificazione
•....
Assunzioni fondamentali della MD
•
Nucleo ed elettroni sono «ammassati» in una sola particella, che rappresenta l'atomo j­esimo nel punto rj.
•
L'energia si conserva a livello microscopico. Quindi le forze
Fj = –∇ jV(r1, r2, r3, ...)
sono scrivibili come i gradienti di un'energia potenziale totale V
•
Le interazioni tra gli atomi che contribuiscono all'energia potenziale sono parametrizzate da forme analitiche più o meno semplici, come potenziali di molle o coulombiani o altri potenziali classici (esempi più tardi). Questa è un'approssimazione poco controllata!
•
L'equazione del moto si integra con algoritmi dove il tempo è “discretizzato” a passettini.
•
Oppure le forze Fj si possono usare per cercare la configurazione piu stabile (minimo dell'energia V)
Energia
Le interazioni determinano la distribuzione spaziale degli atomi e le energie relative che rendono più o meno stabili determinate configurazioni. Le forze sono appunto date da − i gradienti di V
Energia =
energia delle interazioni di legame
+
energia delle interazioni di non legame
Force field: insieme delle equazioni (e dei parametri) che descrivono come varia l'energia quando gli atomi si spostano.
Energia di legame
Esempio di parametrizzazione del campo di forze:
Energia di allungamento
(stretching) dei legami
+
Energia di piegamento
(bending) degli angoli tra coppie di legami
+
Energia di torsione degli angoli diedri
bending
stretching
torsion
Termini di legame: stretching
Energia di stretching: potenziale armonico (molle­legame)
V stretch = ∑
bonds
ks
2
r −r 0 
ks = costante elastica,
r = |rj – rj'| = lunghezza istantanea del legame,
r0 = distanza di equilibrio 2
Termini di legame: bending
Energia di bending: potenziale armonico
V bend =
∑
angles
kθ
2
2
 θ−θ 0 
k = rigidità della molla­angolo,
  = arccos((rj – rj')∙(rj – rj”)/(|rj – rj'| |rj – rj”|)) = angolo istantaneo tra i 2 legami,
0 = angolo di equilibrio Termini di legame: torsione
Energia torsionale:
V t=
∑
torsions
kφ
2
 φ −φ0
2
oppure
V t=
∑
torsions
A[1−cos n φ−φ0  ]
termine armonico (per torsioni rigide di piccola ampiezza)
+
termine sinusoidale (per torsioni “soffici” a 360°): modella la presenza di barriere steriche attraversabili;
A = ampiezza curva,
n = tipo di simmetria e periodicità,
= angolo torsionale d'equilibrio
Interazioni a lunga distanza
• Atomi non legati covalentemente, ad es. atomi della stessa molecola ma separati tra loro da almeno due legami covalenti, oppure atomi di molecole diverse
• In buona approssimazione l'energia di “non­legame” dipende dalle distanze reciproche tra tutte le coppie di atomi non legati
• Esempi principali di interazioni di non­legame: le forze di Van der Waals e quelle elettrostatiche • Sono forze “a lungo raggio”: energie e forze decadono con leggi di potenza a grande distanza tra le coppie di atomi
Interazioni di Van der Waals
Una forza attrattiva (a lunga distanza E ∝ –r­6), dovuta a fluttuazioni nella distribuzione di carica delle nuvole elettroniche.
r*
A piccola distanza questa attrazione di VdW (che divergerebbe a –∞, facendo collassare la simulazione) è bilanciata, e dominata dalla repulsione dovuta al sovrapporsi delle nubi elettroniche (piccola distanza E ∝ +r­12). Repulsione e Le interazioni di Van der Waals attrazione vanno a zero a distanza e gli effetti di repulsione interatomica infinita.
vengono spesso modellizzati Bilanciamento ad una distanza usando il potenziale di Lennard­Jones
intermedia ottimale r*. Interazioni elettrostatiche
Potenziale di Coulomb: rappresenta l’interazione elettrostatica tra una coppia di atomi carichi
1
V Coulomb r 1 , r 2 ,... , r N =
4 0  r
qj qj'
∑ ∣r −r ∣
j j '
j
j'
Interazioni di questo tipo dipendono
• dalla carica atomica qj presente sugli atomi non­legati
• dalla distanza tra atomi non­legati
• dalla natura del dielettrico interposto (può essere sia il solvente che una parte della molecola stessa). Di solito si assegna un valore costante allo schermo  r del dielettrico (tra 1 e 5); si utilizzano valori linearmente dipendenti dalla distanza per simulare effetti dovuti al solvente
Che ce ne facciamo delle Fj?
Cerchiamo il minimo dell'energia potenziale, cioè la configurazione più stabile.
Oppure integriamo l'equazione di Newton e vediamo come la materia si muove.
Minimizzazione energia libera:
guida il folding delle proteine
Ipotesi termodinamica di Anfinsen
Le proteine funzionali assumono spontaneamente un'unica struttura tridimensionale, determinata dalla loro struttura primaria (sequenza)
Questa struttura nativa è il minimo stabile dell'energia libera ed un percorso ragionevolmente “liscio” porta dallo stato unfolded alla struttura nativa.
Lo stato nativo è il minimo assoluto dell’energia libera F della proteina.
Ricerca minimo energetico
Conformazione energeticamente preferita minimo globale dell'energia potenziale equilibrio stabile
stato più popolato a bassa T
... ma...
F = U – T S

L'energia libera F non coincide con l'energia U

È necessario tenere conto anche di termini entropici

Nei calcoli talvolta si usano delle energie potenziali “efficaci” che tengono conto anche dell'entropia
Algoritmi di minimizzazione
Fanno discendere l'energia verso il minimo più vicino Algoritmi principali:
lento ma robusto, senza complicazioni dà • Simplex: strutture di partenza rozze e ad elevata energia
descent: veloce, lavora bene lontano dal • Steepest minimo quando il gradiente è grande
lavora bene solo vicino al minimo; • Newton­Raphson: meno steps per convergere
 meglio usare diversi minimizzatori a turno
Un rischio tipico della minimizzazione
I minimi locali: partendo da configurazioni a casaccio la minimizzazione del potenziale rischia di intrappolarsi in configurazioni molto diverse dal vero minimo
minimo assoluto
configurazione iniziale rischiosa
Un rischio reale: alcune malattie (Alzheimer, BSE, Parkinson) sono legate a misfolding di proteine!
Violazione dell'ergodicità: la proteina non esplora tutto lo spazio delle configurazioni
Dinamica molecolare (MD)
Permette lo studio di processi dinamici complessi che avvengono nei sistemi biologici. Può anche tornare utile a trovare minimi globali (simulated annealing). Descrive allo stesso tempo sia le vibrazioni locali che le transizioni conformazionali, ad esempio:
stabilità delle proteine
variazioni conformazionali
folding proteico
trasporto ionico
Obiettivo della DM
Calcolare la traiettoria di un sistema molecolare cioè
la configurazione molecolare in funzione del tempo,
cioè
come variano nel tempo le posizioni (e dunque anche le velocità e le accelerazioni) di tutti gli atomi della/e molecola/e.
In realtà si parte proprio dalle accelerazioni:
aj = Fj / mj Traiettoria
La traiettoria è generata da integrazioni simultanee dell’equazione del moto di Newton aj = Fj / mj per tutti gli atomi del sistema, nota la forza Fj esercitata dal sistema su ciascun atomo.
La forza è uguale alla derivata dell'energia potenziale:
Fj = – ∂V/∂rj quindi
d2rj /dt2 = – mj­1 ∂V/∂rj che collega la derivata dell'energia potenziale alle variazioni di posizione in funzione del tempo
Ingredienti
• le posizioni iniziali rj degli atomi (coordinate atomiche): si ricavano ad es. da strutture sperimentali (cristallografia raggi X, NMR ecc.) o ottenute con modeling;
• le velocità iniziali vj spesso si ottengono dalla distribuzione delle velocità caratteristica di una data temperatura; • le accelerazioni aj lungo tutta la traiettoria sono determinate dalle derivate dell'energia potenziale totale V
Distribuzione iniziale di velocità vi

Riscaldamento lento alla temperatura di simulazione

Riequilibrazione dell’energia tra gli atomi

Temperatura di simulazione desiderata

Lunga integrazione  energia libera del sistema
Algoritmi di integrazione
Non c'è soluzione analitica all'equazione del moto, data la sua forma complessa (l'energia potenziale è funzione delle 3N coordinate atomiche di tutti gli atomi del sistema) ⇒ soluzione numerica ⇒ algoritmi numerici (es. velocity­Verlet e Runge­Kutta).
Caratteristiche comuni fondamentali degli algoritmi di integrazione:
●
deve valere la conservazione dell'energia e del momento
●
devono essere computazionalmente efficienti
●
●
devono permettere un tempo di integrazione il più lungo possibile
si possono fare simulazioni a energia fissata (ensemble microcanonico) oppure a temperatura fissata (ensemble canonico)
Accuratezza metodo
L'accuratezza della simulazione è limitata da
●
qualità del force­field (= capacità di riprodurre i risultati sperimentali)
●
simulazione dell'ambiente circostante
●
scelta della configurazione di partenza
●
lunghezza del periodo di tempo di equilibrazione
●
lunghezza del tempo di simulazione
●
(alcuni ns)
eventuale importanza di effetti quantistici (mecc. classica 
no livelli vibrazionali discreti, no spettroscopia!)
Un “esperimento” al computer
Evoluzione di proprietà locali (nucleasi dello stafilococco)
Un “esperimento” al computer
2.5 nm
Carbonio
Idrogeno
Azoto
Fluoro
Una simulazione di liquidi ionici: [bmim]+ [Ntf2]− a 300 K
Un “esperimento” al computer
Dynameomics: un pacchetto per analizzare le traiettorie della MD
Un “esperimento” al computer
(movie)
Simulazione MD di un peptide in solvente acquoso
Un “esperimento” al computer
(movie)
Simulazione “parallel tempering” o “replica exchange” MD del folding:
AK­peptide (sequenza AAAAKAAAAKAAAAKAAAAY) in solvente acquoso (non mostrato ma simulato).
A=Alanina, K=Lisina, Y=Tirosina
Un “esperimento” al computer
(movie)
Simulazione replica­exchange MD del folding:
trp­cage miniprotein (sequenza NLYIQWLKDGGPSSGRPPPS) in solvente acquoso (non mostrato ma simulato). È mostrata una
singola replica (di 40) che arriva alla struttura nativa ripiegata in circa 30­40 ns di tempo di simulazione