Introduzione

Rilevazione statistica e inferenza
Censuaria (o esaustiva)
Indagine
statistica
Campionaria
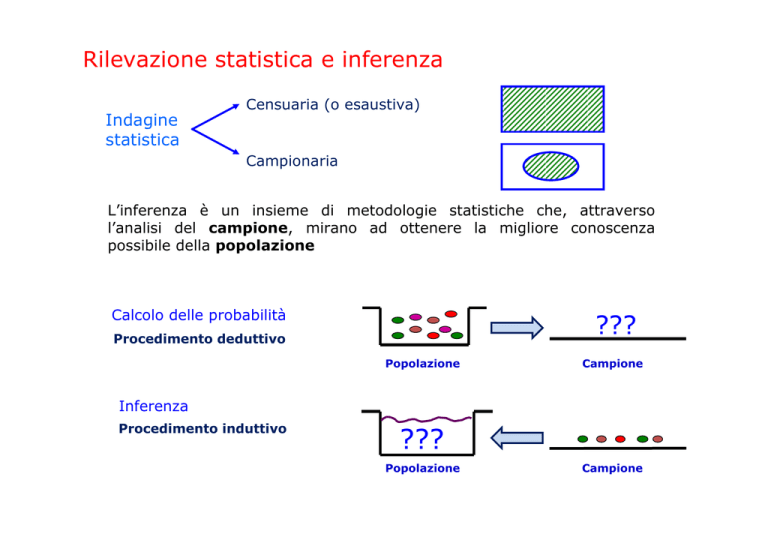
L’inferenza è un insieme di metodologie statistiche che, attraverso
l’analisi del campione, mirano ad ottenere la migliore conoscenza
possibile della popolazione
Calcolo delle probabilità
???
Procedimento deduttivo
Popolazione
Campione
Inferenza
Procedimento induttivo
???
Popolazione
Campione
Procedimento deduttivo
???
Dal generale al particolare
In particolare:
I triangoli rettangoli hanno un angolo retto
A è un triangolo rettangolo
Procedimento induttivo
Dal particolare al generale
In generale:
A ha un angolo retto
???
Popolazione
Campione
1) Si effettua un esperimento (campione)
2) Si generalizzano i risultati
Esempio:
In particolare:
Campione
Conosco la popolazione: che probabilità ho
di estrarre un certo campione?
Esempio:
In generale:
Popolazione
Esame: poche domande (campione)
Livello di preparazione
N.B.: nel procedimento induttivo vi è sempre la possibilità di errore!!!
La probabilità nella Statistica
Popolazione
Il
campionamento
Campione
Estrazione casuale
Logica deduttiva:
Popolazione: Il 40% degli studenti della Facoltà di Economia di Napoli è fuorisede.
Campione: Estraendo a caso 15 studenti, qual è la probabilità che almeno 10 siano fuorisede?
La teoria della probabilità deduce dal contenuto noto della popolazione il contenuto probabile
del campione, deducendo, quindi, le proprietà di un processo fisico da un modello matematico.
Logica induttiva:
Campione: Da un’indagine effettuata su un campione di 250 studenti della Facoltà di Economia
di Napoli è risultato che il 40% erano fuorisede.
Popolazione: Qual è la percentuale di fuorisede dell’intera popolazione di studenti di Economia?
L’inferenza statistica induce le caratteristiche della popolazione dall’analisi del contenuto del
campione osservato, cioè inferisce le proprietà del modello matematico a partire dall’analisi
dei dati campionari che sono stati osservati.
3
L’oggetto dell’analisi statistica
Ottica descrittiva:
Osservazione di un fenomeno su un “insieme” di unità statistiche
Sintesi dell’insieme di unità osservate attraverso il valore assunto
dagli indicatori (media, varianza, ecc.)
Ottica inferenziale:
Insieme
Campione estratto da una popolazione di unità
statistiche
Previsione di quali valori potrebbero assumere i parametri (media,
varianza, ecc.) della popolazione, sulla base dei valori assunti dai
corrispondenti indicatori “campionari” (logica induttiva)
4
Obiettivi
Strumenti
Cosa ci faremo?
inferenza
Probabilità, distribuzioni
campionarie
uso
stima
Stimatori
significato
teorico
descrizione
Indici:
media, varianza, …
calcolo
Il momento dell’analisi
Certezza
Incertezza
Dopo l’osservazione del fenomeno
Prima dell’osservazione del fenomeno
• Variabili statistiche
• Distribuzioni di frequenze
• Rappresentazioni grafiche:
funzione di ripartizione empirica
istogramma (densità di frequenza)
• Variabili casuali: applicazione da Ω in ℜ
• Distribuzioni di probabilità
• Rappresentazioni grafiche:
funzione di ripartizione
funzione di (densità di) probabilità
Densità di
frequenza
-
L’istogramma illustra graficamente l’andamento
di un carattere X, suddiviso in classi, ossia il
modo in cui i valori di X si alternano all’interno
di un insieme di n osservazioni
X
La sua utilità, dunque, interviene dopo l’osservazione delle n unità.
6
Esso serve a descrivere il comportamento del carattere nelle n unità osservate.
Immaginando di suddividere X in classi sempre più piccole, al limite infinitesimali,
l’istogramma può essere approssimato da una curva
Quindi, ragionando al contrario:
Se è nota la funzione descritta graficamente alla curva, si può affermare di
conoscere il comportamento del fenomeno X (anche senza osservarlo)
Problema:
Qual è la forma analitica della funzione che descrive il fenomeno X?
Soluzione:
Si può trattare X come una Variabile Casuale la cui
distribuzione di probabilità sia nota
7
Considerazioni sulla varianza
Ipotesi assurda: varianza = 0
Popolazione X costituita da unità statistiche uguali:
• Campioni tutti uguali
• Nessun rischio di errore nella stima
• Basta osservare una sola unità
Ipotesi realistica: varianza > 0
Popolazione X costituita da unità statistiche diverse:
• Campioni generalmente diversi tra loro
• Rischio di errore nella stima: a seconda del campione
selezionato il risultato sarà diverso
Legame logico tra i principali elementi dell’inferenza
Variabile casuale = distribuzione della variabile casuale
Variabili casuali univariate:
in generale: v.c. discrete e continue
v.c. particolari: Normale, Uniforme continua e discreta, Bernoulli,
Binomiale, Poisson
Variabili casuali doppie:
valore atteso, varianza, covarianza, correlazione (→ regressione)
Combinazioni lineari di variabili casuali:
valore atteso e varianza
Teorema limite centrale:
distribuzione (Normale) della combinazione lineare di v.c. di cui
singolarmente non è nota la distribuzione:
IC e test sulla media
Distribuzioni che derivano dalla Normale:
t di Student: IC e test su: media, coefficienti di regressione
chi-quadro:
test di indipendenza
F di Fisher:
test sull’R2