Distribuzioni di probabilita'
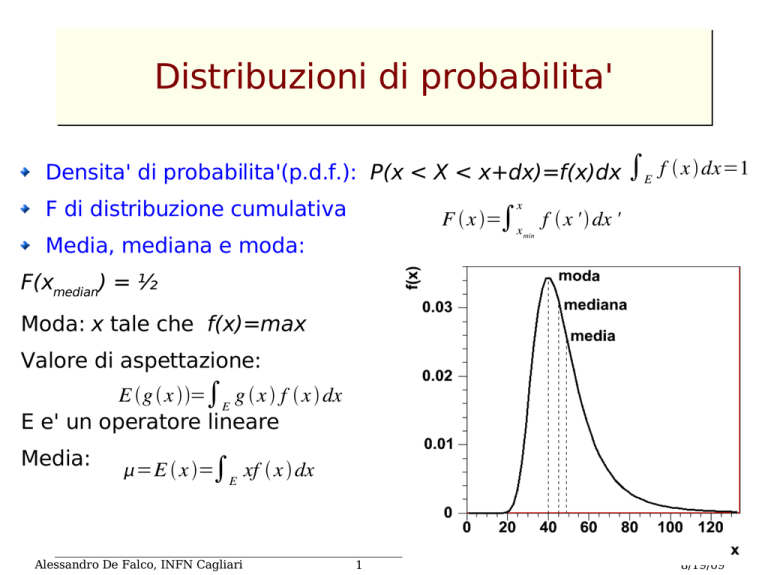
Densita' di probabilita'(p.d.f.): P(x < X < x+dx)=f(x)dx ∫E f x dx=1
x
F di distribuzione cumulativa
F x =∫x
Media, mediana e moda:
min
f x ' dx '
F(xmedian) = ½
Moda: x tale che f(x)=max
Valore di aspettazione:
E g x =∫E g x f x dx
E e' un operatore lineare
Media:
=E x =∫E xf x dx
Alessandro De Falco, INFN Cagliari
1
8/19/09
Varianza e momenti di ordine piu'
alto
Media:
=E x =∫E xf x dx
Varianza:
=E x− =∫E x− f x dx
Momento k-mo intorno alla media:
k =E x− =∫E x− f x dx
2
Coefficiente di asimmetria (skewness):
2
2
k
k
1=
2=
Curtosi:
3
3 /2
2
4
2
2
3
=
E x−
3
−3
Questa definizione implica un confronto con la gaussiana.2>0 (<0) implica che la
distribuzione e' piu' (meno) piccata intorno alla media rispetto ad una distribuzione
normale
1
Vale la diseguaglianza di Bienamye'-Tschebycheff:P∣x−E x ∣≥ ≤ 2
che limita la probabilita' che x si allontani dal valore
medio per un certo numero di deviazioni standard.
Alessandro De Falco, INFN Cagliari
2
8/19/09
Distribuzioni di piu' variabili
Densita' di probabilita' congiunta: f x 1, x 2,. .. x n
∫ f x 1, x 2,. .. x n dx1 dx 2 .... dx n=1
Le regole per il calcolo del valore medio di una funzione,
media, varianza etc si applicano in maniera immediata
Matrice di covarianza:
V ij ≡E x i−i x j− j =∫ x i− i x j− j f x 1, x 2,. .. x n dx 1 dx 2 .... dx n
V e' simmetrica
l' elemento diagonale i-mo Vii=i2 e' detto varianza di xi ed e' non negativo.
L'elemento non diagonale Vij=cov(xi,xj) e' detto covarianza di xi e xj
Viene spesso utilizzato il coefficiente di correlazione
x i , x j =
cov x i , x j
Si dimostra che
i j
Alessandro De Falco, INFN Cagliari
3
−1≤≤1
8/19/09
Le variabili xi sono indipendenti se la loro probabilita' congiunta e'
fattorizzabile: f x x ... , x = f x f x ... f x
1,
n
2,.
1
1
2
n
2
n
In questo caso gli elementi non diagonali della matrice di
covarianza sono nulli. Inoltre E(xixj)=E(xi)E(xj)
Una proiezione della p.d.f. In un sottospazio e' chiamato distribuzione
marginale. Es.:
x max x max
x max
2
h 1 x 1 =
3
∫
....
∫
x 2 min x 3 min
n
∫
x n min
f x 1, x 2,. .. x n dx 2 .... dx n
se le variabili sono indipendenti la p.d.f. congiunta e' fattorizzabile
nelle distribuzioni marginali.
La distribuzione condizionata è definita come
f x 1, x 2,. .. , x n∣x j =
f x 1, x 2,. .. x n
h j x j
Cambiamento di variabili.
y=y x
Nota la pdf f(x) trovare g(y)
Generalizzazione a piu' variabili:
g y=J
Alessandro De Falco, INFN Cagliari
x 1, x 2,. .. , x n
4
y1, y 2,. .. y n
dx
∣ ∣
g y =
dy
f x
f x
8/19/09
Propagazione degli errori
Sia y=y x x .. x = y x
con V x nota. Stimiamo la
varianza di y.
Al primo ordine: y x ≈y ∑ x − ∂ y
1,
2,.
n
n
i
i=1
i
∂ xi
x=
E y x ≈ y
2
V y x =E y x −E y x ≈ E y x−y
n
y x −y ≈∑ x i−i
i=1
n
n
V y x ≈∑ ∑
i=1 j=1
∂y
∂ xi
n
x=
n
V y x ≈∑ ∑
i=1 j=1
∂y
∂ xj
∂y
∂ xi
n
Per variabili indipendenti
V y x ≈∑
i=1
x=
x=
∂y
∂ xi
∂y
∂ xi
2
x=
E xi − i x j − j
∂y
∂ xj
2
x=
x=
V ij x
Legge di propagazione
degli errori
V ii x
Le formule sono generalizzabili al caso di m funzioni yk di n variabili xi
Alessandro De Falco, INFN Cagliari
5
8/19/09
Anticipazioni sul campionamento
La p.d.f. f(x) di una variabile continua x, descrive le
proprieta' di una popolazione (o universo).
Un esperimento consistera' di un numero finito di misure
x1,x2,...xn, che costituiscono un campione.
Due quantita' che caratterizzano il campione sono la media
aritmetica e la varianza:
x=
1
n
∑ xi
n i =1
2
s =
1
n−1
n
∑ x i− x
i=1
2
Necessario perche'
s2 costituisca uno
stimatore senza bias
di σ2
Media e varianza sono ancora variabili casuali
Appartengono alla popolazione normale
Sono indipendenti
La media e' distribuita come una variabile normale
S2 e' legata alla distribuzione di χ2
Gli argomenti accennati in questa trasparenza verranno
approfonditi in seguito
Alessandro De Falco, INFN Cagliari
6
8/19/09
Funzione caratteristica
Data la densita' di probabilita' f(x), consideriamo la funzione caratteristica:
k ≡ f k ≡⟨ eikx ⟩=∫ eikx f x dx
Per variabili continue, la funzione caratteristica e' la trasformata di Fourier di
f(x)
(per variabili discrete:
ikx i
k =∑ e
P x= xi
)
Se f(x) e' la convoluzione di g(x) e h(x), allora la funzione caratteristica di f(x)
e' il prodotto delle funzioni caratteristiche di g(x) e h(x)
f k = g k ⋅ h k
f x= dx ' g x ' h x−x '
∫
Se E(x) = 0
dn
dk n
Inoltre
f x=
0=i n n
1
2
funzione funzione caratteristica caratteristica di f
di g
momento di ordine n
funzione caratteristica di h
∫ e−ikx k dk
La funzione caratteristica congiunta di due variabili indipendenti e' pari al
prodotto delle funzioni caratteristiche delle due variabili, ovvero e' fattorizzabile
Si puo' dimostrare che f(x) e' determinata univocamente dalla sua funzione caratteristica
La funzione caratteristica puo' essere utile nel calcolo
Alessandro De Falco, INFN Cagliari
7
8/19/09
Numeri random
Generazione di numeri casuali al calcolatore
I computers svolgono i calcoli in maniera deterministica!
I numeri generati al computer hanno un numero finito di cifre.
Una variabile potra' essere scritta nella forma
x= a 0 2 0 a1 2 1... a k−1 2 k−1
dove ai potra' essere uguale a 0 o ad 1, con probabilita' 1/2
Una variabile cosi' costruita ammettera' 2k valori diversi possibili.
Se e' possibile estrarre in maniera casuale equiprobabile i valori
degli ai, x avra' una distribuzione uniforme sui 2k valori discreti;
x/2k sara' distribuita tra 0 e 1.
Ogni numero (pseudo)casuale estratto da un computer sara'
funzione dei numeri estratti in precedenza.
x n = f x n −1 , x n −2 , .... x 1
Alessandro De Falco, INFN Cagliari
8
8/19/09
Metodo lineare congruente
Una possibile funzione per la generazione di numeri random a
distribuzione piatta e' data da:
x n = mod ax n−1c , m
In questa maniera generiamo una sequenza con periodicità m
(purchè c e m non abbiano fattori comuni, a-1 sia un multiplo di
tutti i fattori primi di k e a-1 sia multiplo di 4 se m è multiplo di 4)
Ovviamente se durante la sequenza si ripete uno dei numeri
(interi), tutta la sequenza si ripeterà a partire da quel numero
Per ottenere una sequenza abbastanza lunga dobbiamo usare
a ed m abbastanza grandi, ma non tali per cui a*m causa un
overflow
x n =mod ax n−1c , 2 k
Solitamente si usa m=2
k
Un generatore che segue questo algoritmo è un generatore
lineare congruente
Es.: routine drand48 nei sistemi AIX genera numeri random
tra 0 e 1 con buone proprietà spettrali. Drand48 usa k=48,
c=B(hex), a=5DEECE66D(hex)
Alessandro De Falco, INFN Cagliari
9
8/19/09
Esercizio: scrivere un generatore di numeri casuali con
a=5, c=13, k=12
verificare che la periodicita' e' 4096.
verificare che la distribuzione e' piatta
DOPO 150
EVENTI
DOPO 4096
EVENTI
DOPO 40960
EVENTI
(Il contatore in ascisse
viene riazzerato
ogni 4096 eventi)
Alessandro De Falco, INFN Cagliari
10
8/19/09
Effetto Marsiglia
Attenzione alle correlazioni!!!!
Uso il generatore col setting dell'esercizio
precedente, estraggo 3 numeri random in
sequenza, r1,r2,r3, e calcolo r3 vs r2-r1
Osserviamo delle evidenti correlazioni
Random numbers fall mainly in the planes:
n-ple successive di numeri generati da un
MCG si dispongono su (n!2nbits)1/n iperpiani
di uno spazio n dimensionale (effetto Marsiglia)
Provate con a=4097, c=10515, k=18
Il meglio che si può fare è aumentare il
numero di iperpiani con una scelta accorta
di a,c,k
Risultato per il generatore di Root
Alessandro De Falco, INFN Cagliari
11
8/19/09
Numeri casuali con distribuzione data
Calcolo analitico
E' possibile estrarre numeri casuali x con distribuzione f(x) a
partire da un set di numeri casuali y a distribuzione piatta
g(y)=1
Y
X
0
x min
Y =∫ dy= ∫ f x dx=F X
f x dx=g y dy=dy
Se sappiamo integrare f(x), possiamo ricavare X in funzione
di Y.
Estraendo Y con distribuzione piatta tra 0 e 1 otterremo le X
corrispondenti distribuite come f(x)
Esercizio: generare dei numeri random con distribuzioni:
f x=
1
cosh 2 ax
f x=
Alessandro De Falco, INFN Cagliari
Distribuzione simile
ad una gaussiana
1
1 x
12
2
8/19/09
Calcolo numerico
Se non sappiamo integrare f(x) possiamo ancora estrarre numeri casuali
distribuiti secondo f(x) in un intervallo (a,b) procedendo in due modi:
Metodo 1: Calcoliamo numericamente la funzione integrale a passi
discreti e per ogni y ricaviamo la x corrispondente
Normalizzo e
integro f(x) tra -∞
eX
Metodo 2:
✔
✔
✔
✔
✔
Estraggo una Y=F(X)
con distribuzione
piatta...
...Ed ottengo la
X corrispondente
distribuita come
f(x)
Nota: la funzione in questo
esempio puo' essere integrata
analiticamente
Determino fmax nell'intervallo (a,b)
Estraggo x con distribuzione uniforme, in modo che a<= x < b
Estraggo y con distribuzione uniforme, in modo che 0<=y<fmax
Tengo x se y<f(x)
Le x cosi' ottenute sono distribuite secondo la distribuzione f
Alessandro De Falco, INFN Cagliari
13
8/19/09
Metodo Monte Carlo per l'integrazione
di una funzione
Vogliamo determinare l'integrale 1
I 0 =∫ g x dx 0g x 1 per 0 x1
y
0
(xj,yj)
(xi,yi)
Estraggo N coppie (x,y) di numeri random a
distribuzione piatta
Conto il numero K di coppie per cui y<=g(x)
Stimo l'integrale come K/N
Posso generalizzare facilmente il calcolo al
caso xmin<x<xmax mediante la trasformazione
x = xmin + (xmax-xmin) x0-1 0<x0-1<1
ed eseguire un'analoga trasformazione per y
x Il metodo e' inefficiente per funzioni
di singola variabile, ma diventa
potente per funzioni di piu' variabili.
Alessandro De Falco, INFN Cagliari
14
8/19/09
Distribuzione binomiale
Prendo un esperimento che puo' dare due soli risultati A e A'
(E=A+A')
P A= p
P A' =1− p
Ripetiamo n volte l'esperimento
La probabilita' che il risultato dei primi k esperimenti sia A e quello dei
k
n−k
restanti n-k sia A' e'
p 1− p
Si puo' ottenere k volte l'evento A in n esperimenti in un numero di
combinazioni pari a n ! /[ k ! n−k !]
La probabilità P di ottenere k volte A in n esperimenti è dunque
data data dalla:
P k , n , p=
n!
k
n−k
p 1− p
k ! n−k !
Distribuzione binomiale
Valore medio =⟨ k ⟩=∑ k P k =np
Varianza
2
2
2
2
=⟨ k− ⟩=⟨ k ⟩−⟨ k ⟩ =np1− p
La statistica binomiale si applica nel calcolo dell'efficienza
Alessandro De Falco, INFN Cagliari
15
8/19/09
Esempi di distribuzioni binomiali
p
n
Alessandro De Falco, INFN Cagliari
16
8/19/09
Esercizio: l'efficienza di uno scintillatore S viene determinata ponendolo
tra due scintillatori S1 e S2 e contando il numero k di eventi in cui S,S1 e
S2 hanno dato simultaneamente un segnale ed il numero n di eventi in
cui S1 e S2 hanno dato simultaneamente un segnale
(indipendentemente da S).
Eseguendo la misura si ottiene k=97, n=100.
Quale e' il valore dell'efficienza?
Quale e' l'errore?
raggio
cosmico
S1
S
S2
Esercizio 2: efficienza di scanning
Vengono eseguiti due scanning indipendenti su un campione di dati.
Siano ε1 ed ε2 le efficienze di scanning, che supponiamo gia'
determinate
Quale e' l'efficienza dell'OR dei due scanning e quale e' il suo errore?
Alessandro De Falco, INFN Cagliari
17
8/19/09
Statistica multinomiale
Generalizzazione della statistica binomiale. Se i risultati possibili
sono m,
E = A1 A2 ... A m
P Ai = pi
m
∑ pi =1
i=1
la probabilita' di ottenere k1 volte A1,.... km volte Am in n
esperimenti e'
m
n!
k
P k 1, k 2,. .. , k m , n= m
∏ pi
Distribuzione multinomiale
i
∏ ki !
i=1
i=1
Valore medio per 'i-mo evento
Elementi della matrice di covarianza:
⟨ x i ⟩=np i
c ij =npi ij − p j
oss: gli elementi di matrice non diagonali non sono nulli (gli eventi
non sono indipendenti)
Alessandro De Falco, INFN Cagliari
18
8/19/09
Statistica di Poisson
Es. conteggi in uno scintillatore dovuti ad una sorgente
radioattiva
P k , =e
−
k
k!
Valore medio
=⟨ k ⟩=∑ k P k =
Varianza
=⟨ k− ⟩=⟨ k ⟩−⟨ k ⟩ =
2
2
2
2
Per piccoli λ la distribuzione poissoniana e' molto asimmetrica
ed e' caratterizzata da una coda a destra del valore medio
skewness:
1
3=
Alessandro De Falco, INFN Cagliari
19
8/19/09
Esempi di distribuzioni poissoniane
Alessandro De Falco, INFN Cagliari
20
8/19/09
Alessandro De Falco, INFN Cagliari
=0.5
=1
=5
=0.5
=25
21
8/19/09
Statistica poissoniana: assunti
fondamentali
Si puo' ricavare la statistica poissoniana in maniera del tutto
generale sulla base di alcuni assunti.
Otteniamo la formula a partire da un esempio:
Tracciamento in camera a bolle:
Sia g il numero medio di bolle per unita' di lunghezza in una
traccia
consideriamo un tratto (piccolo) ∆l della traccia
Ipotesi:
✔
✔
✔
✔
g e' costante
C'e' al massimo una bolla nel tratto di lunghezza ∆l
La probabilita' di trovare una bolla lungo questo tratto e' proporzionale a ∆l
La presenza di una bolla tra l e l+∆l e' indipendente dalla presenza di bolle in
altri intervalli ad esso non sovrapposti
p1 l =g l
probabilita' di avere una bolla in ∆l
p 0 l =1−g l
probabilita' di avere zero bolle in ∆l
p 0 l l = p 0 l p 0 l = p 0 l 1−g l
p 0 l l − p 0 l
l
p 0 l =e−gl
=−gP 0 l
Alessandro De Falco, INFN Cagliari
22
8/19/09
p n l l = p n l p 0 l p n−1 l p1 l probabilita' di avere n bolle in l+∆l
n bolle in l e 0 in ∆l
n-1 bolle in l e 1 in ∆l
p n l l = p n l 1−g l p n−1 l g l
p n l l − p n l
l
n
gl
P n l =e−gl
n!
=−g P n l − p n−1 l
Esercizio: nella ricerca di correnti neutre deboli, vengono osservati 9
candidati per le reazioni indotte da neutrini
p p0
p n
fondo:
n p n p0
n p nn
Identificando gli eventi di tipo n p p p si stima un fondo di 4.9 ev.
Supposto che il n. di ev. di fondo sia distribuito con statistica poissoniana con
valore medio pari a 4.9, quale e' la probabilita' che 9 o piu' ev. siano di fondo?
−
Alessandro De Falco, INFN Cagliari
23
8/19/09
Statistica binomiale e poissoniana
Esercizio (dalle lezioni di R. Barlow al CERN)
Uno studente fa l'autostop a bordo della strada. Le
automobili transitano con la frequenza di una al minuto,
seguendo la statistica poissoniana. La probabilità che
un'automobile dia un passaggio allo studente è dell'1%.
Quale è la probabilità che lo studente non ottenga un
passaggio:
✔
1- Dopo il transito di 60 automobili
✔
2- Dopo un'ora
Alessandro De Falco, INFN Cagliari
(0.5472)
(0.5488)
24
8/19/09
Confronto tra la statistica binomiale e
poissoniana
Confrontiamo una
distribuzione poissoniana
con λ=3 con due
distribuzioni binomiali per
cui np= λ
Al diminuire di p e al
crescere di n (fissato il
prodotto) la statistica
binomiale approssima con
precisione crescente quella
poissoniana
Alessandro De Falco, INFN Cagliari
25
8/19/09
Sovrapposizione di due sorgenti poissoniane
I decadimenti di due sorgenti radioattive, governati dalla
1medi
2
statistica di Poisson, sono caratterizzati dai valori
e
Si puo' mostrare che i campioni possono essere combinati
mediante una convoluzione
P r =∑ Pr ' , 1 P r−r ' , 2
r'
e che la distribuzione ottenuta e' ancora una poissoniana con
valore medio
1
Alessandro De Falco, INFN Cagliari
2
26
8/19/09
Distribuzione uniforme
Consideriamo una variabile casuale continua x che puo' assumere un
qualunque valore entro un intervallo x1 ≤ x < x2 con la stessa densita' di
probabilita':
f x =c
x1 ≤ x x 2
f x =0
x x 1, x≥ x 2
Poiche' la distribuzione deve essere normalizzata a 1,
f x=
1
x 2 −x 1
f x=0
E x=
x1 ≤xx 2
1
x 2 − x1
x2
∫ x dx=
x1
xx 1, x≥x 2
x 1 x 2
2 x=
2
1
12
x 2 −x 1 2
Esercizio: le dimensioni dei pixel di un rivelatore sono 0.04 mm. Non viene
registrata l'informazione sull'ampiezza del segnale e un solo pixel viene acceso dal
passaggio della particella. Quale e' la risoluzione spaziale del rivelatore a pixel?
La distribuzione uniforme e' usata estensivamente nelle simulazioni
Monte Carlo, dove si trasformano numeri casuali a distribuzione piatta in
numeri casuali con qualsivoglia distribuzione
Alessandro De Falco, INFN Cagliari
27
8/19/09
Distribuzione gaussiana
La distribuzione gaussiana (o normale) e' data da:
f x=
1
2
exp −
µ=valore medio
σ2=varianza
La gaussiana e'
simmetrica intorno
al valore medio
1 x−2
2
2
=0
=1
∫− f x dx=0.683
2
∫
f x dx=0.955
−2
3
∫
f x dx=0.997
−3
0.68
0.95
0.997
Esercizio: calcolare il rapporto tra FWHM e σ
(FWHM= larghezza a meta' altezza)
Alessandro De Falco, INFN Cagliari
28
8/19/09
Funzione caratteristica della gaussiana
t =E eitx =e
Alessandro De Falco, INFN Cagliari
1
i t− 2 t 2
2
29
8/19/09
Teorema di addizione per variabili con
distribuzione gaussiana
E' spesso utile conoscere la distribuzione di una grandezza che e'
funzione di variabili con distribuzione gaussiana.
In particolare, possiamo essere interessati ad una combinazione
lineare di variabili distribuite normalmente.
Siano x1 e x2 due variabili casuali con distribuzione normale N(µ1,σ12) e
N(µ2,σ22)
e y=a1x1+a2x2. Calcoliamo le funzioni caratteristiche
a1 1 it−
a x t =e
1
1
2
a21 21 t 2
1
a
2
x2
t =e
1
a 2 2 it − a 22 22 t 2
2
Se le variabili sono indipendenti
la f. caratteristica e' fattorizzabile
1
a1 1 a2 2 it−
y t =a
1
x1
t a
2
x2
t =e
2
a 21 12a22 22 t 2
Dunque, una combinazione lineare di due variabili casuali x1 e x2 con
distribuzione normale N(µ1,σ12) e N(µ2,σ22), y=a1x1+a2x2 e' anch'essa
distribuita con distribuzione normale
N a1 1a 2 2, a 21 21 a22 22
Alessandro De Falco, INFN Cagliari
30
8/19/09
Teorema del limite centrale
Supponiamo di avere n variabili indipendenti xi (i=1,...n) generate
da una distribuzione qualunque avente media µ e varianza σ2.
Per n→∞ la loro media aritmetica tende ad una gaussiana avente
media µ e varianza σ2/n.
n
xi
i =1
n
x =∑
f x ∝ exp −
Alessandro De Falco, INFN Cagliari
1 x −2
2 2 / n
31
8/19/09
Somma di n numeri distribuiti
uniformemente
Tiriamo un dado. Il valore risultante sara' una variabile
casuale a valori interi distribuita uniformemente tra 1 e 6
Lanciamo il dado n volte e facciamo la media dei risultati.
Eseguiamo l'operazione per
un certo numero di volte
e mettiamo in un istogramma
la distribuzione
dei valori ottenuti
I grafici riportati sono le
distribuzioni ottenute per
diversi valori di n
Alessandro De Falco, INFN Cagliari
32
8/19/09
Una nota sulla programmazione
Macro di root che produce il grafico della slide precedente
void CLT(Int_t nev=300000){ TCanvas *c1= new TCanvas("c1","c1"); c1­>Divide(3,3); for (Int_t n=1; n<=9; n++) { c1­>cd(n); THF *h1=new TH1F("h1","",7*n*4,0,7); for (Int_t iev=0; iev<nev; iev++){ nota: se anziche' sommare tutti Float_t average = 0; gli addendi e poi dividere per n for (Int_t isum=0; isum<n; isum++) { avessi calcolato direttamente la Int_t x = Int_t(gRandom­>Rndm()*6) + 1; media con average += Float_t(x); }
average += Float_t(x)/n; average /=n;
il risultato sarebbe stato h1­>Fill(average); quello riportato in figura
}
h1­>Draw(); char txt[20];
sprintf(txt,"n=%d",n); TText *text = new TText (0.2,h1­>GetMaximum()*0.9,txt); text­>SetTextSize(0.1); text­>Draw(); c1­>Update();
}
Esercizio: scrivere un programma che calcola media
}
}
aritmetica e deviazione standard per ciascuna delle
distribuzioni ottenute al variare di n
Alessandro De Falco, INFN Cagliari
33
8/19/09
Distribuzioni normali multivariate
Una funzione di due variabili indipendenti con distribuzione
normale sara' distribuita secondo la:
f x , y =
1
−
2 x y
e
2
1 x− x
2
2x
−
e
2
1 y− y
2
2y
Se le variabili non sono indipendenti, la distribuzione sara':
f x , y =
1
−
2 x y 1−
Alessandro De Falco, INFN Cagliari
2
e
1
2
2 1−
34
x− x
2
x
2
y− y
2
y
2
−2
x− x y− y
xy
8/19/09
Distribuzione del χ2
Se {x1, x2, x3, ...xn} sono n variabili distribuite
con pdf gaussiana, la quantita'
n
2 = ∑
x i −i
2
2i
i =1
e' distribuita secondo la:
f z , n=
z n/2−1 e−z /2
2 n /2 n / 2
Dove la∞funzione Gamma di Eulero e' definita come:
x −t
x1=∫ t e dt
0
Alessandro De Falco, INFN Cagliari
x 1= x x
35
1
2
=
1=1
8/19/09
Densita' di probabilita' del χ2
Il numero n e' detto
numero di gradi di liberta'.
La distribuzione della somma
di due differenti distribuzioni
di χ2 con n1 e n2 gradi di liberta'
e' ancora un χ2 con n=n1 + n2
gradi di liberta'
Il valore di aspettazione di un
χ2 con n d.o.f. e' pari ad n
Ndf = 1,3,5,7,9
2
χ
Distribuzione cumulativa del χ
2
La varianza e' pari a 2n.
χ2
Alessandro De Falco, INFN Cagliari
36
8/19/09