Teorema di Pitagora - SCUOLA SECONDARIA DI I GRADO “G

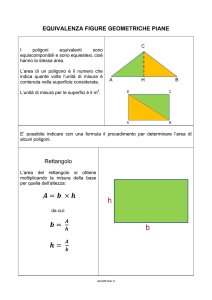
TEOREMA DI PITAGORA
Enunciato
In un triangolo rettangolo il quadrato
costruito sull’ipotenusa è equivalente
alla somma dei quadrati costruiti sui
cateti
𝒊𝟐 = 𝒄𝟏 𝟐 + 𝒄𝟐 𝟐
𝒄𝟏 𝟐 = 𝒊𝟐 − 𝒄𝟐 𝟐
𝒄𝟐 𝟐 = 𝒊𝟐 − 𝒄𝟏 𝟐
𝒊=
𝒄𝟏 𝟐 + 𝒄𝟐 𝟐
𝒄𝟏 =
𝒊𝟐 − 𝒄𝟐 𝟐
𝒄𝟐 =
𝒊𝟐 − 𝒄𝟏 𝟐
GEOMETRIA 40
Esempio:
I cateti di un triangolo rettangolo misurano rispettivamente 15 cm e 20 cm.
Determina la misura dell’ipotenusa.
Dati
Incognita
𝐴𝐵 = 15 𝑐𝑚
𝐵𝐶 = ?
𝐴𝐶 = 20 𝑐𝑚
Risoluzione
𝐵𝐶 =
𝐴𝐵 2 + 𝐴𝐶 2
𝐵𝐶 =
152 + 202 =
GEOMETRIA 41
225 + 400 =
625 = 25 𝑐𝑚
Applicazioni del Teorema di Pitagora
Rettangolo
𝒅=
𝒃𝟐 + 𝒉𝟐
𝒉=
𝒅𝟐 − 𝒃𝟐
𝒃=
𝒅𝟐 − 𝒉𝟐
Esempio:
Calcola la misura della diagonale di un rettangolo, sapendo che la base misura 4,8
cm e l’altezza misura 2 cm.
Dati
Incognita
𝐴𝐵 = 4,8 𝑐𝑚
𝐵𝐷 = ?
𝐴𝐷 = 2 𝑐𝑚
Risoluzione
𝐵𝐶 =
𝐴𝐵 2 + 𝐴𝐷 2
𝐵𝐶 =
4,82 + 22 =
GEOMETRIA 42
23,04 + 4 =
27,04 = 5,2 𝑐𝑚
Quadrato
𝒍𝟐 + 𝒍𝟐 =
𝒅=
=
𝒍𝟐 × 𝟐
𝒍𝟐 × 𝟐 = 𝒍 ×
𝒍=
𝟐
𝒅
𝟐
Le formule relative al quadrato si
utilizzano per i triangoli rettangoli
isosceli con gli angoli acuti di 45°.
Esempio:
Calcola la misura della diagonale di un quadrato, il cui lato misura 8 cm
Dati
Incognita
𝐴𝐵 = 8 𝑐𝑚
𝐵𝐷 = ?
Risoluzione
𝐵𝐶 = 𝐴𝐵 ×
2
𝐵𝐶 = 8 ×
2 = 8 × 1,41 = 11,28 𝑐𝑚
GEOMETRIA 43
Triangolo isoscele
𝟐
𝒍=
𝒃
𝒉𝟐 +
𝟐
𝟐
𝒉=
𝒃
𝟐
𝒍 −
𝟐
𝒃
=
𝟐
𝒍𝟐 − 𝒉 𝟐
Esempio:
In un triangolo isoscele la base misura 6 cm e l’altezza misura 4 cm; calcola la
misura del perimetro.
Dati
Incognita
𝐴𝐵 = 6 𝑐𝑚
2𝑝 = ?
𝐶𝐻 = 4 𝑐𝑚
Risoluzione
𝐵𝐶 =
𝐶𝐻2 +
𝐴𝐵 2
2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 × 2
𝐵𝐶 =
42 +
6 2
2
= 42 + 32 =
2𝑝 = 6 + 5 × 2 = 6 + 10 = 16 𝑐𝑚
GEOMETRIA 44
16 + 9 =
25 = 5 𝑐𝑚
Triangolo equilatero
𝒉=
𝒍𝟐 −
𝟐
𝒍𝟐 −
=
𝒍𝟐
𝟒
=
𝟒𝒍𝟐 − 𝒍𝟐
=
𝟒
=
=
𝒍 𝟐
𝟑𝒍𝟐
𝟑 × 𝒍𝟐
=
=
𝟒
𝟒
𝟑×𝒍
𝟐
Ricorda:
𝟑
= 𝟎, 𝟖𝟔𝟔
𝟐
Da cui deriva:
𝒍=
𝟐 ×𝒉
𝟑
Le formule relative al triangolo
equilatero si utilizzano per i triangoli
rettangoli con un angolo acuto di 30°
e l’altro di 60°
GEOMETRIA 45
Esempio:
Calcola la misura dell’altezza di un triangolo equilatero sapendo che il lato misura 5
cm.
Dati
Incognita
𝐴𝐵 = 5 𝑐𝑚
𝐶𝐻 = ?
Risoluzione
𝐶𝐻 =
𝐶𝐻 =
𝐴𝐵 × 3
2
3
2
× 5 = 0,866 × 5 = 4,33 𝑐𝑚
Rombo
𝒍=
𝒅𝟏
𝟐
𝟐
𝟐
𝒅𝟐
+
𝟐
𝒅𝟏
=
𝟐
𝒅𝟐
𝟐
𝒍 −
𝟐
𝟐
𝒅𝟐
=
𝟐
𝒅𝟏
𝟐
𝒍 −
𝟐
𝟐
GEOMETRIA 46
Esempio:
L’area di un rombo è di 1176 cm2 e la diagonale maggiore misura 56 cm; calcola la
misura del perimetro.
Dati
Incognita
𝐵𝐷 = 56 𝑐𝑚
2𝑝 = ?
𝐴 = 1176 𝑐𝑚2
O
Risoluzione
𝐷𝐵 =
𝐴 ×2
𝐵𝐷
𝐴𝐵 =
𝐴𝐶
2
𝐷𝐵 =
2
+
𝐵𝐷
2
2
𝐴𝐵 =
=
1176 × 2
= 42 𝑐𝑚
56
56
2
2
42
+
2
784 + 441 =
Trapezio rettangolo
𝟐
+ 𝒉𝟐
𝒍=
𝒃𝟏 − 𝒃𝟐
𝒉=
𝒍𝟐 − 𝒃𝟏 − 𝒃𝟐
𝟐
𝒍𝟐 − 𝒉 𝟐
GEOMETRIA 47
=
282 + 212
1225 = 35 𝑐𝑚
2𝑝 = 35 × 4 = 140 𝑐𝑚
2𝑝 = 𝐴𝐵 × 4
𝒃𝟏 − 𝒃𝟐 =
2
Esempio:
Calcola la misura del perimetro di un trapezio rettangolo, sapendo che le due basi
misurano rispettivamente 18 cm e 28 cm e l’altezza misura 24 cm.
Dati
Incognita
𝐴𝐵 = 28 𝑐𝑚
2𝑝 = ?
𝐶𝐷 = 18 𝑐𝑚
𝐶𝐻 = 24 𝑐𝑚
Risoluzione
𝐻𝐵 = 𝐴𝐵 − 𝐷𝐶
𝐵𝐶 =
𝐶𝐻 2 + 𝐻𝐵 2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐶𝐷 + 𝐷𝐴
𝐻𝐵 = 28 − 18 = 10 𝑐𝑚
𝐵𝐶 =
242 + 102 =
576 + 100 =
2𝑝 = 28 + 26 + 18 + 24 = 96 𝑐𝑚
GEOMETRIA 48
676 = 26 𝑐𝑚
Trapezio isoscele
𝟐
𝒍=
𝒃𝟏 − 𝒃𝟐
𝟐
𝒉=
𝒃𝟏 − 𝒃𝟐
𝟐
𝒍 −
𝟐
𝒃𝟏 − 𝒃𝟐
=
𝟐
+ 𝒉𝟐
𝟐
𝒍𝟐 − 𝒉 𝟐
Esempio:
Calcola la misura del perimetro di un trapezio isoscele, sapendo che le due basi
misurano rispettivamente 52 cm e 28 cm e l’altezza misura 9 cm.
Dati
Incognita
𝐴𝐵 = 52 𝑐𝑚
2𝑝 = ?
𝐶𝐷 = 28 𝑐𝑚
𝐶𝐻 = 9 𝑐𝑚
Risoluzione
𝐻𝐵 =
𝐵𝐶 =
𝐴𝐵 − 𝐷𝐶
2
𝐶𝐻 2 + 𝐻𝐵 2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐶𝐷 + 𝐷𝐴
𝐻𝐵 =
𝐵𝐶 =
52− 28
2
= 12 𝑐𝑚
92 + 122 =
81 + 144 =
2𝑝 = 52 + 15 + 28 + 15 = 110 𝑐𝑚
GEOMETRIA 49
225 = 15 𝑐𝑚