GEOM_07_Equivalenza figure piane

EQUIVALENZA FIGURE GEOMETRICHE PIANE
I
poligoni
equivalenti
sono
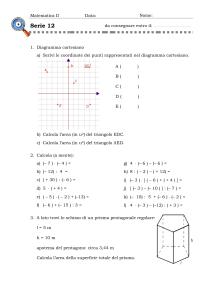
equiscomponibili e sono equiestesi, cioè
hanno la stessa area.
L’area di un poligono è il numero che
indica quante volte l’unità di misura è
contenuta nella superficie considerata.
L’unità di misura per le superfici è il m2.
E’ possibile indicare con una formula il procedimento per determinare l’area di
alcuni poligoni.
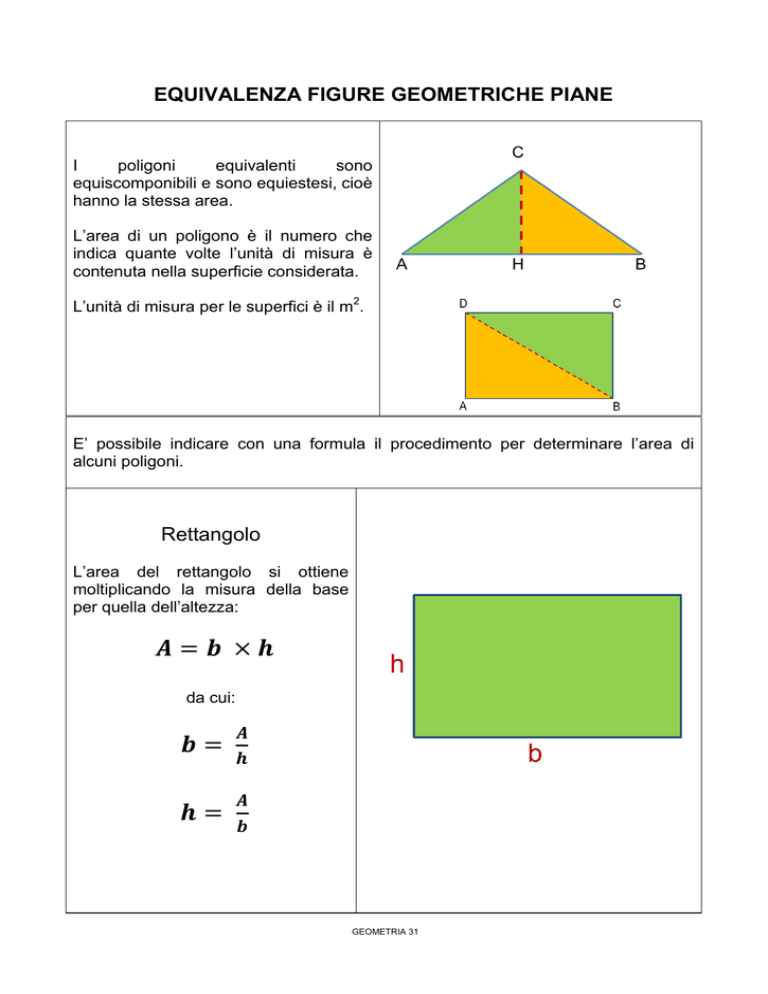
Rettangolo
L’area del rettangolo si ottiene
moltiplicando la misura della base
per quella dell’altezza:
𝑨=𝒃 ×𝒉
da cui:
𝒃=
𝒉=
𝑨
𝒉
𝑨
𝒃
GEOMETRIA 31
Esempio:
Calcola l’area di un rettangolo, sapendo che la base misura 5 cm e l’altezza misura
2 cm.
Dati
Incognita
𝐴𝐵 = 5 𝑐𝑚
𝐴 =?
𝐴𝐷 = 2 𝑐𝑚
Risoluzione
𝐵𝐶 = 5 × 2 = 10 𝑐𝑚2
𝐴 = 𝐴𝐵 × 𝐴𝐷
Quadrato
L’area del quadrato di ottiene
moltiplicando la misura del lato per
se stessa:
𝑨 = 𝒍 × 𝒍 = 𝒍𝟐
da cui:
𝒍=
𝑨
GEOMETRIA 32
Esempio:
Calcola il perimetro di un quadrato, la cui area misura 144 cm2
Dati
𝐴 = 144 𝑐𝑚2
Incognita
2𝑝 = ?
Risoluzione
𝐴𝐵 = 𝐴
2𝑝 = 𝐴𝐵 × 4
𝐴𝐵 = 144 = 12 𝑐𝑚
2𝑝 = 12 × 4 = 48 𝑐𝑚
GEOMETRIA 33
Parallelogrammo
L’area del parallelogrammo si ottiene
moltiplicando la misura della base
per quella dell’altezza:
𝑨=𝒃 ×𝒉
da cui:
𝒃=
𝒉=
𝑨
𝒉
𝑨
𝒃
Esempio:
Calcola l’area di un rettangolo, sapendo che la base misura 15 cm e l’altezza
misura 4 cm.
Dati
𝐴𝐵 = 15 𝑐𝑚
Incognita
𝐴 =?
𝐷𝐻 = 4 𝑐𝑚
Risoluzione
𝐴 = 𝐴𝐵 × 𝐷𝐻
𝐵𝐶 = 15 × 4 = 60 𝑐𝑚2
GEOMETRIA 34
Triangolo
L’area del triangolo si ottiene
moltiplicando la misura della base
per quella della relativa altezza e
dividendo il prodotto ottenuto per
due:
𝑨=
𝒃×𝒉
𝟐
da cui:
𝒃=
𝒉=
𝑨×𝟐
𝒉
𝑨×𝟐
𝒃
Esempio:
Un triangolo di area 25 dm2 ha la base che misura 10 dm. Calcola la misura
dell’altezza.
Dati
Incognita
𝐴 = 25 𝑑𝑚2
𝐶𝐻 = ?
𝐴𝐵 = 10 𝑑𝑚
Risoluzione
𝐶𝐻 =
𝐴 ×2
𝐴𝐵
𝐶𝐻 =
25 ×2
10
= 5 𝑐𝑚
GEOMETRIA 35
Triangolo rettangolo
𝑨=
𝒄𝟏 ×𝒄𝟐
𝑨=
𝟐
𝒊×𝒉
𝟐
da cui:
𝒄𝟏 =
𝒄𝟐 =
𝒊=
𝑨×𝟐
𝒄𝟐
𝑨×𝟐
𝒄𝟏
𝑨×𝟐
𝒉
Esempio:
L'area di un triangolo rettangolo è 96 dm2 e il cateto minore misura 12 dm. Calcola
la misura dell'altro cateto.
Dati
Incognita
𝐴 = 96 𝑑𝑚2
𝐴𝐶 = ?
𝐴𝐵 = 12 𝑑𝑚
Risoluzione
𝐴𝐶 =
𝐴 ×2
𝐴𝐵
𝐴𝐶 =
96 ×2
12
= 16 𝑐𝑚
GEOMETRIA 36
Triangolo – formula di Erone
𝑨=
𝟐𝒑
𝟐
×
𝟐𝒑
𝟐
− 𝒂 ×
𝟐𝒑
𝟐
− 𝒃 ×
a, b ,c: misure dei lati
2p: perimetro
Rombo
L’area del rombo si ottiene
moltiplicando la misura delle due
diagonali e dividendo il prodotto
ottenuto per due:
𝑨=
𝒅𝟏 × 𝒅𝟐
𝟐
da cui:
𝒅𝟏 =
𝒅𝟐 =
𝑨×𝟐
𝒅𝟐
𝑨×𝟐
𝒅𝟏
GEOMETRIA 37
𝟐𝒑
𝟐
− 𝒄
Esempio:
Le diagonali di un rombo sono una tripla dell'altra e la loro somma misura 16,8 cm.
Calcola l'area.
Dati
Incognita
𝐵𝐷 = 3 × 𝐴𝐶
𝐴=?
𝐴𝐶 + 𝐵𝐷 = 16,8 𝑐𝑚
Risoluzione
𝐴𝐶 =
𝐴𝐶 + 𝐵𝐷
𝐴𝐶 =
4
𝐵𝐷 = 3 × 𝐴𝐶
𝐴=
16,8
4
= 4,2 𝑐𝑚
𝐵𝐷 = 3 × 4,2 = 12,6 𝑐𝑚
(𝐴𝐶 × 𝐵𝐷 )
𝐴=
2
4,2 × 12,6
2
=
52,92
2
= 26,46 𝑐𝑚2
Trapezio
L’area del trapezio si ottiene
moltiplicando la misura della somma
delle due basi per la misura
dell’altezza e dividendo il prodotto
ottenuto per due:
𝑨=
𝒃𝟏 + 𝒃𝟐 × 𝒉
𝟐
da cui:
𝒉 =
𝑨×𝟐
𝒃𝟏 + 𝒃𝟐
𝒃𝟏 + 𝒃𝟐 =
𝑨×𝟐
𝒉
GEOMETRIA 38
Esempio:
Calcola l'area di un trapezio che ha la base maggiore lunga 6,4 cm, la minore lunga
4,8 cm e l'altezza 3,2 cm.
Dati
Incognita
𝐴𝐵 = 6,4 𝑐𝑚
𝐴 =?
𝐷𝐶 = 4,8 𝑐𝑚
𝐶𝐻 = 3,2 𝑐𝑚
Risoluzione
𝐴=
𝐴𝐵 + 𝐷𝐶 × 𝐶𝐻
2
𝐴=
6,4 + 4,8 × 3,2
GEOMETRIA 39
2
=
35,84
2
= 17,92 𝑐𝑚2