PROBLEMA 1. In laboratorio è stato preparato il dispositivo

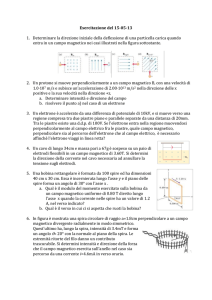
PROBLEMA 1.
In laboratorio è stato preparato il dispositivo rappresentato in Figura1. La bobina è
costituita da 100 spire rettangolari di rame i cui lati misurano 25 cm e 30 cm. La
bobina può ruotare con attrito trascurabile intorno al suo asse e durante la rotazione le
estremità del filo strisciano su due anelli conduttori, mantenendo con essi un contatto
elettrico. La bobina è immersa in un campo magnetico uniforme e costante.
Sull’asse della bobina è montato un cilindro intorno al quale è avvolto un filo.
All’estremità del filo è sospeso un pesetto. Quando il pesetto viene lasciato libero,
esso cade verso il basso mettendo in rotazione la bobina. Alla partenza del pesetto il
piano della spira è perpendicolare alla direzione del campo magnetico.
Durante la rotazione della bobina, alle sue estremità, che restano aperte in modo che
non circoli corrente, si produce una f.e.m. il cui valore viene rilevato da un sistema di
acquisizione automatico che acquisisce 1000 valori al secondo.
In Figura 2 sono stati riportati i dati sperimentali acquisiti dal sistema. Questo grafico
rappresenta in ordinata la f.e.m. prodotta alle estremità della bobina durante la caduta
del pesetto ed in ascissa il tempo.
La Figura 3 rappresenta lo stesso grafico di Figura 2. In quest’ultimo grafico i punti
sperimentali sono stati uniti da segmenti per migliorarne la leggibilità.
Figura 1
Contatti
striscianti
Contatti
striscianti
Al misuratore
di f.e.m
1) Spiega il fenomeno fisico che produce la f.e.m. alle estremità della bobina e, sulla
base di esso, spiega il particolare andamento del grafico sperimentale.
2) Utilizza la legge del fenomeno fisico per dedurre teoricamente la funzione
matematica 𝑦 = 𝑓(𝑡) che descrive la f.e.m. alle estremità della bobina in funzione del
tempo everifica che la funzione ottenuta, coerentemente con il grafico sperimentale,
abbia ampiezza crescente e periodo decrescente. Considera l’intensità del campo
magnetico B e l’accelerazione angolare  della bobina come parametri. Considera
inoltre aperte le estremità della bobina.
3) Deduci dal grafico sperimentale le informazioni quantitative necessarie per
determinare il valore dell’accelerazione angolare della bobina e l’intensità del campo
magnetico in cui ruota la bobina.
4) Spiega qual è il significato fisico dell’area, evidenziata in Figura 3, compresa tra
ogni semiperiodo e l’asse dei tempi. Verifica, utilizzando la funzione 𝑦 = 𝑓(𝑡), che
queste aree hanno, in modulo, tutte lo stesso valore.
Figura 2
Figura 3
PROBLEMA 2.
Negli anni 1963-1964 il fisico W. Bertozzi con la sua equipe realizzò un esperimento
al MIT di Boston verificando l’esistenza di una velocità limite, pari a quella della
luce nel vuoto.
Secondo la fisica classica è possibile accelerare un corpo dalla quiete fino a una
velocità qualunque, per quanto grande essa sia, mentre per la relatività questo non è
possibile.
L’esperimento consiste nell’accelerare elettroni attraverso opportuni campi elettrici
prodotti da una un acceleratore di Van de Graaff e da un acceleratore lineare a
radiofrequenza (LINAC). Il fascio di elettroni è prodotto da un catodo caldo,
sottoforma di impulsi della durata di 3 ns (3 ∙ 10−9 𝑠𝑒𝑐) e viene accelerato
dall’acceleratore di Van de Graaff attraverso differenze di potenziale variabili fino a
un massimo di 1,5 milioni di volt.
Gli elettroni, usciti dall’acceleratore di Van de Graaff, attraversano un tubicino
metallico posto in A nel quale inducono un impulso di corrente che viene inviato
all’oscilloscopio (vedi Figure 1 e 2). Il tragitto da A e B è lungo 8,40 m ed è privo di
aria e di campi elettrici che possano modificare la velocità degli elettroni
(l’acceleratore LINAC è spento in una prima fase dell’esperimento e in particolare
non è utilizzato nelle prime tre misure di sotto riportate). Arrivati in B gli elettroni
urtano un disco di alluminio nel quale provocano un impulso di corrente che viene
inviato anch’esso all’oscilloscopio. Sull’oscilloscopio la distanza tra i due impulsi dà
la misura del tempo impiegato dagli elettroni per andare da A a B e quindi, nota la
distanza AB, è possibile calcolare la loro velocità.
Ogni quadretto del reticolo dell’oscilloscopio (divisione) corrisponde ad un tempo di
circa (0,98 ∙ 10−8 𝑠𝑒𝑐).
LINAC =1,00 m
Fonte: http://giulioannovi.altervista.org/fisica/quinta/Energiacineticarelativistica.pdf
Figura 1
Figura 2
Impulsi provenienti da A e da B
Leggendo sull’oscilloscopio la distanza tra i due impulsi, al variare della differenza di
potenziale applicata dall’acceleratore agli elettroni, si ottengono i seguenti valori
(Tabella 1).
Differenza Potenziale
10 V 
6
N° divisioni tra i due
impulsi
0,5
1,0
1,5
3,30 3,10 2,95
Tabella 1
In una seconda fase dell’esperimento, per aumentare ulteriormente l’energia degli
elettroni viene utilizzatoanche l’acceleratore lineare (LINAC) presente nel primo
metro successivo al punto A, nel quale gli elettroni vengono accelerati da ulteriori 3,0
milioni di volt.
Nell’esperimento viene anche misurato il calore prodotto dagli elettroni sul disco B
adoperando una termocoppia, e la carica incidente sullo stesso disco B, per mezzo di
un misuratore di cariche. I risultati ottenuti per due diversi valori di differenza di
potenziale complessiva sono (Tabella 2):
Differenza Potenziale
10 V 
6
1,5
4,5
Energia del fascio in B
10,0 29,2
(J)
Carica del fascio in B
6,1 6,1
(μC)
Tabella 2
Dopo questa breve esposizione, ti viene richiesto di:
1) Analizzare l’esperimento descritto e rappresentare in un piano cartesiano
l’andamento di
𝑣2
𝑐2
, dove 𝑣 è la velocità degli elettroni nel punto B e 𝑐 è la
velocità della luce nel vuoto, in funzione del lavoro W compiuto dal campo
elettrico nell’acceleratore, sia per i valori di velocità previsti dal modello
classico che per i valori effettivamente misurati nell’esperimento.
2) Individuare il modello fisico più adatto a descrivere la situazione sperimentale,
relativamente all’andamento di
campo elettrico nell’acceleratore.
3) Calcolare i valori di
𝑣2
𝑐2
𝑣2
𝑐2
in funzione del lavoro W compiuto dal
attesi in base al modello fisico individuato,
confrontandoli con quelli sperimentali e discutere l’andamento atteso.
4) Verificare, utilizzando i dati di Tabella 2 nei casi di differenza di potenziale 1,5
e 4,5 milioni di volt, che l’energia cinetica posseduta dagli elettroni quando
arrivano in B è circa uguale a quella fornita dall’acceleratore, giustificando
così la seguente affermazione: “Il fatto che il valore della velocità misurata sia
inferiore a quello previsto dalla fisica classica non è dovuto a perdite di energia
nell’apparato”.
QUESTIONARIO
1. Una lampadina a incandescenza di potenza 𝑃 = 100𝑊 emette luce in maniera
isotropa. Se viene posta al centro di una stanza cubica di lato 𝐿 = 7𝑚, quanta
energia arriverà in 10 minuti sul soffitto della stanza?
2. Un elettrone e un positrone (antiparticella dell’elettrone con la stessa massa
dell’elettrone, ma con carica opposta) si muovono uno contro l’altro con la stessa
velocità. L’energia posseduta da entrambe le particelle è di 1,51 𝑀𝑒𝑉.
𝑀𝑒𝑉
Sapendo che la loro massa a riposo è di 0,511 2 , qual è la velocità del positrone
nel sistema di riferimento dell’elettrone?
𝑐
3. Un atomo di idrogeno si trova in uno stato eccitato dopo aver assorbito un fotone
ultravioletto di lunghezza d’onda 𝜆 = 97,2 𝑛𝑚.
Questo atomo può riportarsi allo stato fondamentale seguendo diverse transizioni
a ognuna delle quali corrisponde la emissione di luce di una particolare lunghezza
d’onda.
Quante sono le transizioni possibili che provocano emissione di fotoni con
lunghezza d’onda diversa da quella del fotone assorbito?
Quali tra queste transizioni provocano emissione nel visibile?
(costante di Rydberg: 𝑅 = 1,0974 ∙ 107 𝑚−1 )
4. Un’antenna ricevente semplificata è costituita da una spira di rame di forma
quadrata. Il lato della spira misura 20 cm e le sue estremità sono collegate ad un
voltmetro. Quest’ultimo è impostato in modo da fornire il valore efficace della
f.e.m. ai capi della spira, ovvero
(𝑓. 𝑒. 𝑚. )𝑒𝑓𝑓 =
(𝑓. 𝑒. 𝑚. )𝑚𝑎𝑥
√2
dove (𝑓. 𝑒. 𝑚. )𝑚𝑎𝑥 è il valore massimo di una f.e.m. alternata.
L’antenna ricevente è posta a 100m dall’antenna di una radio ricetrasmittente.
Quest’ultima è del tipo utilizzato dai radioamatori.
Queste radio trasmettono ad una frequenza di 27 𝑀𝐻𝑧 e la legge impone loro di
trasmettere con una potenza non superiore a 4𝑊 per non disturbare la ricezione
delle trasmissioni radiofoniche e televisive. Talvolta i radioamatori non rispettano
questo limite e trasmettono con potenze che possono arrivare a 200𝑊.
Si vuole stabilire se la ricetrasmittente in esame rispetta il limite di potenza
imposto dalla legge.
Il nostro voltmetro misura il massimo della f.e.m. quando il piano della spira è
parallelo alla direzione di propagazione dell’onda e perpendicolare al campo
magnetico, come mostrato in figura.
Il valore efficace di questa f.e.m. è di 12,5 𝑚𝑉.
Qual è la potenza emessa dall’antenna della ricetrasmittente?
Y
Campo
elettrico
Z
Campo
magnetico
spira
V
5. Nel grafico sono rappresentati i livelli energetici di una particella di massa m
confinata in una buca di potenziale infinita unidimensionale (detta anche pozzo).
Utilizzando il principio di de Broglie e assumendo chela funzione d’onda
stazionaria si annulli sui bordi della buca, determinala massa della particella.
6. La figura riportata di seguito mostra come varia la sensibilità relativa percentuale
del nostro occhio al variare della lunghezza d’onda nello spettro visibile. Il
massimo della sensibilità (posto pari a 100%) si ha per λ = 555nm.
Fonte: http://www.progettazioneottica.it/unita-fotometriche-lumen-candele-lux/1172
NOTA: La sensibilità assolutadel nostro occhio per una particolare lunghezza
d’onda è definita come il rapporto tra l’energia che viene inviata dalla retina al
cervello (ad esempio sotto forma di corrente elettrica) e l’energia dell’onda
elettromagnetica incidente sulla retina. La sensibilità relativa percentuale per
una particolare lunghezza d’onda è definita come il rapporto tra la sensibilità
assoluta a quella lunghezza d’onda e la sensibilità assoluta alla lunghezza
d’onda λ=555 nm, il tutto moltiplicato per 100.
Utilizzando i dati del grafico di figura (usa solo le lunghezze d’onda per cui sono
riportati i valori della sensibilità relativa percentuale in forma numerica) traccia un
grafico approssimativo che indichi di quanto deve aumentare l’intensità della
radiazione incidente sulla retina dell’occhio, in modo che l’energia inviata dalla
retina al cervello alle varie lunghezze d’onda sia la stessa (si ponga uguale a 1
l’intensità pari alla massima sensibilità relativa).
Determina, inoltre, quanti fotoni a 𝜆 = 650𝑛𝑚 devono giungere sulla retina
affinché essa invii al cervello la stessa energia che invia quando su di essa
giungono 1000 fotoni di lunghezza d’onda 𝜆 = 555𝑛𝑚.
Soluzioni della simulazione della seconda prova di Fisica a.s. 2016/17 – 25 ottobre 2016 A cura di Gianni Melegari, Steave Selvaduray e Claudio Romeni Problema 1
1) La f.e.m. alle estremità della bobina è generata dall’effetto della forza di Lorentz che, durante la
rotazione della bobina, agisce sui portatori di carica liberi presenti nei fili. Questo è uno dei casi
descritti dal fenomeno dell’induzione elettromagnetica che si modellizza con la legge di Faraday!
Neumann, considerando la variazione del flusso attraverso una superficie S che ha per contorno la
bobina. Nel seguito indicheremo con N il numero di avvolgimenti della bobina stessa.
2) Il testo del problema, dicendo di trattare l’accelerazione angolare come un parametro fisso, da
determinare, suggerisce di modellizzare il moto della bobina, per effetto della discesa del pesetto,
come un moto circolare uniformemente accelerato. Il modulo α dell’accelerazione angolare, che di
solito si definisce in modo elementare come
Δω
α=
,
Δt
andrebbe in realtà inteso come una funzione del tempo α(t), ottenuta derivando rispetto a t
l’ulteriore funzione ω(t) che fornisce la velocità angolare del moto di rotazione:
dω(t )
α(t ) =
;
dt
a sua volta, ω(t) è la derivata della funzione θ(t ) che fornisce la variazione nel tempo dell’angolo di
!
rotazione, che qui conviene definire come l’angolo formato tra il vettore campo magnetico B e il
!
vettore superficie S :
dθ(t )
ω(t ) =
.
dt
Nel caso in esame α(t) = α è una costante; quindi, integrando, la legge che fornisce la velocità
angolare è
ω(t ) = ∫ α(t )dt = α∫ dt = αt + ω0 ,
dove ω0 è la costante di integrazione, che risulta pari al valore di ω(t) all’istante t = 0 s a cui inizia
il moto di rotazione.
In maniera analoga la funzione θ(t ) si ottiene come
1
θ(t ) = ∫ ω(t ) dt = ∫ (αt + ω0 ) dt = αt 2 + ω0t + θ0 ,
2
dove θ0 è un’ulteriore costante di integrazione, uguale al valore dell’angolo θ(t ) all’istante t = 0 s.
Dal testo si deduce che valgono le relazioni θ0 = 0 rad e ω0 = 0 rad/s, per cui le leggi del moto
circolare uniformemente accelerato in esame sono
⎧ω = αt
⎪
(1)
⎨
1 2.
⎪⎩θ = 2 αt
!
Sulla base delle formule (1), il flusso di campo magnetico attraverso la superficie S si scrive come
© Zanichelli 2016 !
⎛1
⎞
(2)
Φ S! ( B ) = NBS cosθ = NBS cos ⎜ αt 2 ⎟ .
⎝2
⎠
Quindi la forza elettromotrice misurata ai capi della bobina si calcola come
dΦ ! (t )
⎛1
⎞
y = f (t ) = − S
= NBS α t sen ⎜ αt 2 ⎟ .
(3)
dt
⎝2
⎠
L’ampiezza A(t) della funzione ora ottenuta ha la forma
(4)
A (t ) = N BS α t
ed evidentemente è crescente in modo lineare con il tempo, come affermato nel testo.
Inoltre gli zeri della funzione f(t) si localizzano ponendo
1 2
αt = k π ( k ∈!)
2 k
e quindi corrispondono agli istanti di tempo
2k π
(5)
tk =
.
α
Allora la durata Tk di una mezza rotazione, cioè la distanza temporale tra due zeri consecutivi della
funzione y = f(x), risulta:
(
)
2( k + 1)π
2k π
2π
−
=
k +1 − k .
α
α
α
È interessante studiare la derivata della funzione y = g ( x) = x + 1 − x ; per x > 0, essa risulta
T k = t k +1 − t k =
(6)
dg ( x )
1
1
x − x +1
(7)
=
−
=
.
dx
2 x +1 2 x
2 x x +1
Visto che la funzione x è crescente in tutto il suo dominio, la funzione (7) è sempre negativa.
Questo è vero anche se si sceglie x = k > 0, per cui la successione Tk risulta sempre decrescente.
Dal punto di vista fisico, la durata delle rotazioni diminuisce perché, con il progressivo scendere del
pesetto, la velocità angolare di rotazione aumenta. Per la stessa ragione aumenta!l’ampiezza della
forza elettromotrice indotta, che dipende dalla rapidità con cui varia il flusso Φ S! ( B ).
c) Un semplice grafico mostra che i dati sperimentali sono in ottimo accordo con il modello che
prevede un aumento dell’ampiezza di oscillazione direttamente proporzionale al tempo.
Le due rette disegnate hanno equazioni y = ± A(t ) = ± N BS α t.
© Zanichelli 2016 Quindi il coefficiente lineare della retta che collega (per esempio) i massimi di oscillazione può
essere determinata scegliendo un solo punto sperimentale. Risulta particolarmente comodo
utilizzare il penultimo massimo, a cui si può assegnare ordinata pari a 0,20 V e ascissa (letta sul
grafico) uguale a 0,89 s. Di conseguenza, il coefficiente angolare di quella retta ha valore
0, 20 V
T ⋅ m2
(8)
N BS α = m =
= 0, 22 2 .
0,89 s
s
Inoltre si può utilizzare la formula (5) con il lo zero di ascissa 0,90 s, a cui corrisponde il valore k =
21 (ottenuto contando semplicemente il numero di intersezioni del grafico sperimentale con l’asse t.
In questo modo si ottiene
2k π 42π
42π
rad
(9)
α= 2 = 2 =
= 1, 6 ×102 2 .
2
tk
t21
(0,90 s)
s
Inserendo il dato (9) nella formula (8) si trova
m
0, 22 T ⋅ m2 s 2
(10)
B=
=
= 1,8 ×10−4 T.
2
2
N S α 100 × ( 0, 25 m ) × ( 0,30 m ) × 1,6 ×10 rad s
(
)
Naturalmente, scegliendo altri punti sperimentali si raggiungono gli stessi risultati.
4) La parte di piano evidenziata in nero nella figura 3 è uguale al modulo della variazione del flusso
di campo magnetico durante una metà della rotazione completa. A sua volta, questa variazione
positiva del flusso è uguale al flusso Φ (t4 ) all’istante t4 a cui viene sottratto il flusso Φ(t5 )
all’istante t5 :
Φ(t4 ) − Φ(t5 ) = Φ(t4 ) − [−Φ(t4 )] = 2Φ(t4 ) = 2 N BS.
Il problema chiede però di verificare questa affermazione utilizzando esplicitamente la forma della
relazione funzionale y = f(x).
Per ottenere un risultato positivo si può generalizzare l’esempio precedente ponendo k = 2n , n ∈!;
si è così condotti a calcolare l’integrale
In =
t 2 n +1
∫
t
2n
2(2 n +1)π α
f (t ) dt =
∫
4n π α
2(2 n +1)π α
f (t ) dt =
∫
4n π α
⎛1
⎞
N B S α t sen ⎜ αt 2 ⎟ dt .
⎝2
⎠
Una primitiva della funzione integranda è già nota, ed è l’opposto del flusso (2). Quindi si ottiene
2(2 n +1)π α
⎡
⎛1
⎞⎤
I n = ⎢ − N B S cos ⎜ αt 2 ⎟ ⎥
= − N B S cos (2n + 1)π + N B S cos 2n π = 2 N B S . (11)
⎝2
⎠ ⎦ 4n π α
⎣
È così confermato il risultato dedotto prima da considerazioni generali.
(
)
(
)
© Zanichelli 2016 Problema 2
1) La Figura 1 può essere schematizzata nel seguente modo
in cui viene evidenziato, in particolare, il moto di un elettrone di carica −𝑒. Più precisamente,
l’elettrone viene emesso da un catodo caldo posto in O. Si assume per semplicità che la velocità di
emissione dell’elettrone sia pari a 0 m/s. La particella entra in una regione in cui agisce un campo
elettrostatico uniforme e quindi esce da tale regione, nel punto P, con una velocità 𝑣.
Tale velocità si ottiene attraverso l’uguaglianza fra il lavoro positivo (lavoro motore) compiuto dal
campo elettrico e l’energia cinetica. Dopodiché, l’elettrone arriva al punto A e giunge al punto B
indisturbato oppure soggetto a un’ulteriore accelerazione se il LINAC è acceso.
Un oscilloscopio collegato ad A e a B permette di conoscere il tempo impiegato dall’elettrone a
percorrere la distanza fra tali punti. Infine, l’elettrone scarica la sua energia in B che viene misurata
attraverso la quantità di calore assorbita in tale punto.
Nella risoluzione del problema si assumono i seguenti valori numerici
𝑐 = 2,99792458 ∙ 10! m/s (velocità della luce)
𝑚 = 9,1093826 ∙ 10!!" kg (massa dell’elettrone)
−𝑒 = −1,60217653 ∙ 10!!" C (carica dell’elettrone)
inoltre, la distanza 𝑑, presente in figura, vale, in base al testo del problema, 8,40 m.
Dopo questa premessa, è possibile procedere all’analisi del rapporto
!!
!!
in relazione al lavoro 𝑊
compiuto dal campo elettrostatico sul generico elettrone nel caso in cui il LINAC sia spento.
L’applicazione del teorema di conservazione fra i punti O e P, permette di dedurre la seguente
relazione
𝑊 = 𝐾,
dove 𝑊 = 𝑒∆𝑉 ( ∆𝑉 è la differenza di potenziale generata dalla macchina di Van de Graaff) e
!
𝐾 = ! 𝑚𝑣 ! è l’espressione classica dell’energia cinetica della particella.
© Zanichelli 2016 Da tale relazione si ottiene immediatamente
𝑣! =
2𝑊
.
𝑚
Dividendo quest’ultima per 𝑐 ! , si ricava
𝑣 ! 2𝑊
=
.
𝑐 ! 𝑚𝑐 !
Siccome in questo problema ci sono vari modi di determinare la velocità, quella ottenuta con metodi
classici viene indicata con 𝑣!" ; dunque, si ha
𝑣!" ! 2𝑊
=
.
𝑐!
𝑚𝑐 !
Dalle informazioni contenute nel testo del problema possiamo ipotizzare che la velocità
dell’elettrone sia costante dal punto P al punto B, poiché si assume che esso proceda in uno spazio
in cui sia stato realizzato il vuoto spinto e che il LINAC sia spento; inoltre, dato il rapidissimo
tempo di transito, si trascura la caduta di questa particella nel campo gravitazionale.
Allora il valore della velocità, che indichiamo con 𝑣!" , poiché viene determinata in modo diretto, è
dato da
𝑣!" =
𝑑
,
∆𝑡
dove ∆𝑡 è il tempo segnato dall’oscilloscopio. Da questa formula segue immediatamente
𝑣 ! !"
𝑑!
=
.
𝑐!
𝑐 ! ∆𝑡 !
Nella Tabella 1 del testo la prima riga fornisce tre valori della differenza di potenziale ∆𝑉, mentre la
seconda riga moltiplicata per 0,98 ∙ 10!! s (tempo corrispondente a un quadretto del reticolo),
fornisce tre valori del tempo ∆𝑡.
Dopo questa premessa, è possibile costruire le seguenti tabelle:
Tabella sperimentale
∆𝑉 (10! V)
𝑊 = 𝑒∆𝑉 (J)
0,50
1,0
1,5
8,0 ∙ 10!!"
1,6 ∙ 10!!"
2,4 ∙ 10!!"
𝑁 = Numero
∆𝑡 =
divisioni tra i = 𝑁 ∙ 0,98 ∙ 10!! (s)
due impulsi
3,30
3,2 ∙ 10!!
3,19
3,0 ∙ 10!!
2,95
2,9 ∙ 10!!
𝑣 ! !"
𝑑!
=
𝑐!
𝑐 ! ∆𝑡 !
0,77
0,87
0,94
Tabella teoria classica
∆𝑉 (10! V)
𝑊 = 𝑒∆𝑉 (J)
0,50
1,0
1,5
8,0 ∙ 10!!"
1,6 ∙ 10!!"
2,4 ∙ 10!!"
𝑣!" ! 2𝑊
=
𝑐!
𝑚𝑐 !
2,0
3,9
5,9
© Zanichelli 2016 L’analisi dell’ultima colonna mette bene in evidenza la difficoltà di ottenere i valori sperimentali di
velocità con metodi classici. Secondo un modello classico la discordanza tra i valori sperimentali
delle velocità e quelli teorici potrebbe essere dovuta a fenomeni di dissipazione di energia. Nel
modello relativistico, invece, i valori teorici ottenuti classicamente sono assurdi poiché la velocità
della luce è la velocità limite imposta dalle leggi della fisica.
È a questo punto possibile rappresentare i grafici delle funzioni
! ! !" !!" !
!!
,
!!
in relazione a 𝑊.
2) Dopo aver constatato, nel punto 1, che la meccanica classica non è in grado di ottenere i valori
sperimentali di velocità, poiché i valori teorici di velocità superano la velocità della luce e
comunque non sono in accordo con i dati sperimentali, conviene utilizzare la teoria della relatività
ristretta per spiegare i risultati sperimentali ricavati. A tale scopo, è bene partire dalla formula
relativistica dell’energia cinetica 𝐾:
𝐾 = 𝑚𝑐 !
1
𝑣
1− 𝑐
!
−1 ,
poiché l’unica punto debole del modello classico risiede nell’uso dell’espressione non relativistica
di tale forma di energia.
Attraverso semplici passaggi algebrici, si ricava
𝑣!
=1−
𝑐!
1
𝐾
1+
𝑚𝑐 !
!.
Quando l’elettrone di carica −𝑒 arriva in P, il lavoro 𝑊 = 𝑒∆𝑉 del campo elettrostatico si ritrova
sotto forma di energia cinetica della particella in questione, per cui si ha
𝑣!
=1−
𝑐!
1
𝑊
1+
𝑚𝑐 !
!.
La velocità 𝑣 ottenuta viene indicata con 𝑣!" ; dunque, si deduce
© Zanichelli 2016 𝑣!" !
=1−
𝑐!
1
𝑊
1+
𝑚𝑐 !
!.
3) La formula precedente permette di ottenere la seguente tabella:
Tabella teoria relativistica
∆𝑉 (10! V)
0,5
1,0
1,5
𝑊 = 𝑒∆𝑉 (J)
𝑣!" !
=1−
𝑐!
8,0 ∙ 10!!"
1,6 ∙ 10!!"
2,4 ∙ 10!!"
1
1+
𝑊
𝑚𝑐 !
!
0,74
0,89
0,94
I valori dell’ultima colonna sono in buon accordo con quelli dell’ultima colonna della tabella
sperimentale. È a questo punto possibile rappresentare i grafici delle funzioni
a 𝑊.
! ! !" !!" !
!!
,
!!
in relazione
4) In questo punto si considera anche l’azione del LINAC. L’unica variante, rispetto al caso di
LINAC spento, è che l’elettrone entrando in questo acceleratore subisce un ulteriore incremento di
energia a quindi di velocità. Di conseguenza, la sua velocità nel punto B non ha più modulo 𝑣 ma 𝑣′
con 𝑣 ! > 𝑣.
© Zanichelli 2016 Il lavoro 𝑊!"#$%& fornito dal sistema degli acceleratori relativo al fascio di elettroni di carica
complessiva −𝑞 è dato da
𝑊!"#$%& = 𝑊 + 𝑊 ! ,
dove 𝑊 e 𝑊′ sono rispettivamente il lavoro fornito dal generatore di Van de Graaff e quello fornito
dal LINAC (è diverso da zero se questo acceleratore è acceso). Naturalmente, per il teorema di
conservazione dell’energia, si ha
𝑊 = 𝐾,
dove K è l’energia cinetica del fascio di elettroni in P o in 𝐴! (ingresso al LINAC). Quando il fascio
entra nel LINAC, la variazione di energia cinetica 𝐾 ! − 𝐾 , all’uscita dall’acceleratore, cioè in 𝐵! , è
data da
𝐾! − 𝐾 = 𝑊 !,
da cui segue immediatamente
𝐾 ! = 𝐾 + 𝑊 ! = 𝑊 + 𝑊 ! = 𝑊!"#$%&
𝐾 ! è l’energia del fascio misurata in B sotto forma di quantità di calore assorbita in tale punto.
Questa relazione mette in evidenza come il lavoro fornito dagli acceleratori si ritrova sotto forma di
energia cinetica del fascio di elettroni.
Dopo questa premessa, si osserva che la tabella 2 permette di calcolare il lavoro 𝑊!"#$%& fornito dal
sistema degli acceleratori relativo al fascio di elettroni attraverso la moltiplicazione, in colonna, fra
la prima riga (differenza di potenziale) e la seconda (la carica va espressa in C); dunque, si ha
Energia del fascio in B (J)
10,0
29,2
∆𝑉 (V)
1,5 ∙ 10!
4,5 ∙ 10!
𝑞 (C)
6,1 ∙ 10!!
6,1 ∙ 10!!
𝑊!"#$%& = 𝑞∆𝑉 (J)
9,2
27
I valori dell’ultima colonna sono prossimi ai valori della prima colonna e ciò permette di concludere
(come si afferma nel testo) che non c’è perdita di energia. Di conseguenza l’esperimento di W.
Bertozzi (1963-64) può essere spiegato attraverso la teoria della relatività ristretta di A. Einstein
(1905) e quindi ne costituisce una conferma.
© Zanichelli 2016 Quesito 1
L’energia irradiata 𝐸 da una sorgente di potenza 𝑃 nel tempo ∆𝑡 è data dalla seguente formula
𝐸 = 𝑃 ∙ ∆𝑡.
Nel caso in questione si ha
s
𝐸 = 100 W ∙ 10 min ∙ 60 min = 6,0 ∙ 10! J.
L’energia emessa dalla lampadina si propaga all’ambiente come energia luminosa, ma anche
attraverso uno scambio di calore (si parla in modo esplicito di una lampada a incandescenza).
L’ipotesi più semplice è che i flussi di energia siano isotropi. In questo modo la sorgente, posta al
centro del cubo, irradia allo stesso modo 6 facce quadrate identiche, e così l’energia che arriva nel
soffitto in 10 minuti è la seguente
𝐸soffitto =
!
!
= 1,0 ∙ 10! J.
Quesito 2
Indicando con 𝑚 la massa di entrambe le particelle in gioco, si deduce che la loro energia 𝐸! a
riposo è data da
𝐸! = 𝑚𝑐 ! = 0,511 Mev.
Essendo l’energia totale 𝐸, rispetto al riferimento di laboratorio ℛ, di ciascuna particella pari a
1,51 Mev, l’energia cinetica 𝐾 dell’elettrone o del positrone è data da
𝐾 = 𝐸 − 𝐸! = 1,00 Mev.
Ricordando l’espressione di 𝐾
© Zanichelli 2016 1
𝐾 = 𝑚𝑐 !
𝑣
1− 𝑐
!
−1 ,
si deduce il modulo della velocità delle particelle rispetto a ℛ
𝑣 =𝑐 1−
(osserva che
!
!! !
!
! !
!! !
!!
= 2,82 ∙ 10! m/s
= 1,00/0,511). Per calcolare la velocità 𝑣′ del positrone rispetto all’elettrone
(sistema di riferimento ℛ′ con asse 𝑥′ orientato come l’asse 𝑥 di ℛ), basta ricordare la formula di
composizione relativistica della velocità; nel caso in questione, si ha
𝑣! =
!!!!
!!
!! !
!
=−
!!
!!
!! !
!
= −2,99 ∙ 10! m/s.
Si osservi come la velocità trovata ha le prime tre cifre significative identiche a quelle della velocità
della luce, nonostante ciò, essa è minore di 𝑐 poiché il positrone ha massa non nulla e nessun corpo
dotato di massa può raggiungere la velocità della luce. A conferma, se si ripetono i calcoli con una
cifra significativa in più si ottiene 𝑣 ! = −2,992 ∙ 10! m/s, mentre la velocità della luce nel vuoto
vale 𝑐 = −2,998 ∙ 10! m/s.
Quesito 3
L’equazione
1
1
1
= 𝑅 ! − ! 𝑛! , 𝑛! ∈ ℕ − 0 , 𝑛! < 𝑛! ,
λ
𝑛! 𝑛!
determina le lunghezze d’onda λ delle righe spettrali dell’atomo d’idrogeno.
Quando l’elettrone, che si trova nello stato fondamentale 𝑛! = 1, riceve il fotone di lunghezza
d’onda λ = 9,72 ∙ 10!! m, si porta nello stato caratterizzato dal seguente 𝑛!
𝑛! =
𝑅λ
≈4
𝑅λ − 1
Per determinare il numero di transizioni, esclusa la transizione che porta direttamente allo stato
fondamentale, si riporta la seguente figura esplicativa.
© Zanichelli 2016 Il numero dei casi elencati è 7, ma ci sono solo 5 transizioni distinte.
Si tratta ora di stabilire quali transizioni provocano emissione nel visibile, cioè si tratta di
determinare quelle transizioni caratterizzate dall’emissione di un fotone con lunghezza d’onda
λ ∈ λ!"# = 3,80 ∙ 10!! m, λ!"# = 7,50 ∙ 10!! m . Per ottenere tali transizioni, occorre studiare la
seguente disequazione che segue dalla formula di Rydberg
1
λ!"# 𝑅
1
1
1
!− ! ≤λ
𝑛! 𝑛!
!"# 𝑅
≤
che, dopo aver sostituito i valori numerici agli estremi, diventa
1
1
! − ! ≤ 0,24. (∗)
𝑛! 𝑛!
0,12 ≤
Le due transizioni segnate nella figura in nero forniscono
Tran. 4 ⟶ 3
!
!
soddisfa (∗))
Tran. 3 ⟶ 1
!
𝑛! = 4, 𝑛! = 3 ⟹ !! − !! = 0,05 (fuori dalla banda del visibile perché non
𝑛! = 3, 𝑛! = 1 ⟹
soddisfa (∗))
!
!!!
!
−
!
!!!
= 0,89 (fuori dalla banda del visibile perché non
Le due transizioni segnate nella figura in verde forniscono
!
!
Tran. 4 ⟶ 2
𝑛! = 4, 𝑛! = 2 ⟹ !! − !! = 0,19 (nella banda del visibile perché soddisfa (∗))
Tran. 2 ⟶ 1
𝑛! = 2, 𝑛! = 1 ⟹ !! − !! = 0,75 (fuori dalla banda del visibile perché non
!
!
!
!
!
soddisfa (∗))
!
Delle tre transizioni segnate nella figura in blu, solo una non è ancora stata analizzata:
!
!
Tran. 3 ⟶ 2 𝑛! = 3, 𝑛! = 2 ⟹ !! − !! = 0,14 (nella banda del visibile perché soddisfa (∗))
!
!
Riassumendo, le uniche transizioni nel visibile sono 4 ⟶ 2 e 3 ⟶ 2 e sono contenute nella serie
di Balmer.
Quesito 4
Nelle condizioni illustrate nel disegno la componente z del campo magnetico può essere scritta
come
Bz (t ) = B0 cos(ωt ),
dove B0 è il massimo modulo del campo magnetico variabile e la pulsazione ω vale
rad
ω = 2πf = 2π× 27 ×106 Hz = 1, 7 ×108
.
s
Visto che il campo magnetico e il vettore superficie dell’antenna ricevente hanno la stessa
direzione, la forza elettromotrice indotta nell’antenna quadrata si calcola come
(
)
© Zanichelli 2016 !
d ⎡ S B cos(ωt ) ⎤⎦
dΦ( B )
f em (t ) = −
=− ⎣ 0
= S B0 ω sen(ωt ).
dt
dt
Il valore efficace della forza elettromotrice indotta, vale, quindi
SB ω
fem, eff = 0 .
2
Da quest’ultima formula si ricava B0 come
B0 =
2 f em, eff
Sω
=
(
2 1, 25 ×10−2 V
( 0, 20 m )
2
(1, 7 ×10
8
)
rad s
)
= 2, 6 ×10−9 T.
L’intensità dell’onda elettromagnetica è descritta dall’irradiamento
ΔP 1
1
1 2 2 1 B02
Ee =
= cε 0 E02 = c
c B0 = c
=
ΔS 2
2 µ0c 2
2 µ0
(
)
2
2, 6 ×10−9 T
1⎛
W
8 m⎞
= ⎜ 3, 00 ×10
= 8,1×10−4 2 .
⎟
−7
2
2⎝
s ⎠ 4π×10 N A
m
Se si fa l’ipotesi che l’antenna della radio ricetrasmittente irraggi in modo isotropo, la sua potenza P
può essere determinata come
W⎞
2 ⎛
P = 4πr 2 Ee = 4π× (100 m ) × ⎜ 8,1×10−4 2 ⎟ = 1, 0 ×102 W.
m ⎠
⎝
Considerando che l’antenna, posta vicino al terreno, irraggi su una semisfera, si ottiene almeno una
potenza di 50 W. In entrambi i casi la stazione trasmittente non rispetta le norme di legge.
Quesito 5
Per risolvere il quesito si può considerare uno qualunque dei livelli energetici che compaiono nella
figura; per esempio il secondo, a cui corrisponde un’energia
J
E2 = 9, 4 eV = 9, 4 eV ×1, 602 ×10−19
= 1,5 ×10−18 J.
eV
In analogia con gli stati stazionari di una corda vibrante, la lunghezza d’onda λ 2 dell’onda di de
Broglie relativa al primo stato eccitato (n = 2) è uguale alla larghezza della buca, per cui vale
λ 2 = 0, 4 nm = 4 ×10−10 m.
Dalla relazione di de Broglie si ottiene, quindi, che la quantità di moto p2 corrispondente è
h 6, 626 ×10−34 J ⋅ s
m
=
= 1, 66 ×10−24 kg .
−10
λ2
4 ×10 m
s
L’energia della particella nella buca di potenziale è esclusivamente cinetica e quindi l’energia E2
del primo stato eccitato è data all’espressione
p2
E2 = 2 .
2m
È quindi possibile calcolare
p2 =
(
)
2
1, 66 ×10−24 kg ⋅ m s
p22
m=
=
= 9 ×10−31 kg.
2 E2
2 ×1,5 ×10−18 J
Il risultato, fornito con una sola cifra significativa perché anche il dato su λ 2 ne ha una sola, è
compatibile con il valore 9,11×10−31 kg della massa dell’elettrone.
© Zanichelli 2016 Quesito 6
Dai dati della curva di sensibilità si deduce il seguente grafico, in cui le ordinate sono
semplicemente l’inverso della sensibilità dell’occhio alle corrispondenti lunghezze d’onda.
L’energia E di un fotone di frequenza f quindi lunghezza d’onda λ è data dalla formula
c
E = hf = h .
λ
Per fare in modo che N2 fotoni di lunghezza d’onda λ 2 = 650 nm forniscano al cervello la stessa
energia dovuta a N1 = 1000 fotoni con lunghezza d’onda λ1 = 555 nm, l’energia totale dei primi
deve essere uguale a quella dei secondi, moltiplicata per il fattore correttivo 1/0,11. Si ottiene così
la condizione
c
1
c
N2 h
=
N1 h ,
λ 2 0,11
λ1
da cui si ottiene il risultato
λ 1000 650 nm
1
N2 =
N1 2 =
= 1,1×104.
0,11 λ1 0,11 555 nm
© Zanichelli 2016