Distribuzione dei numeri palindromi
Nella breve trattazione che segue cercheremo di ricavare qualche proprietà dei numeri palindromi e di
sfruttarla per trarre una stima approssimativa della loro evoluzione percentuale.
Un numero di dice palindromo quando leggendolo da sinistra a destra mantiene lo stesso valore che assume
leggendolo da destra a sinistra. Ad esempio:
55, 121, 2552, 18981, ...
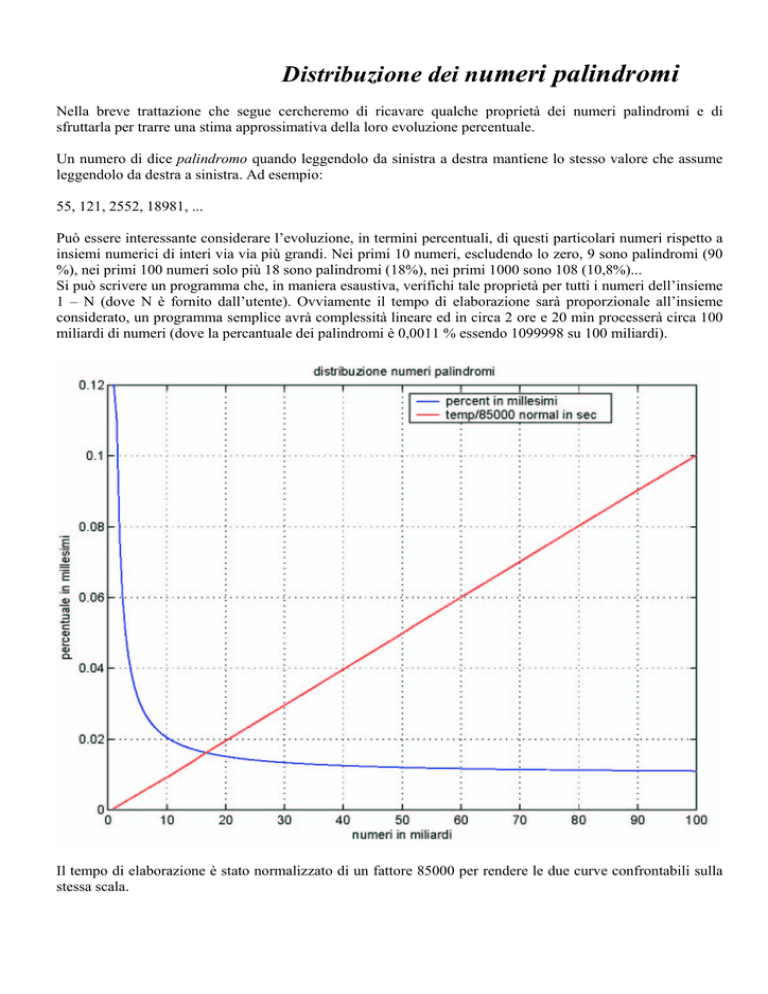
Può essere interessante considerare l’evoluzione, in termini percentuali, di questi particolari numeri rispetto a
insiemi numerici di interi via via più grandi. Nei primi 10 numeri, escludendo lo zero, 9 sono palindromi (90
%), nei primi 100 numeri solo più 18 sono palindromi (18%), nei primi 1000 sono 108 (10,8%)...
Si può scrivere un programma che, in maniera esaustiva, verifichi tale proprietà per tutti i numeri dell’insieme
1 – N (dove N è fornito dall’utente). Ovviamente il tempo di elaborazione sarà proporzionale all’insieme
considerato, un programma semplice avrà complessità lineare ed in circa 2 ore e 20 min processerà circa 100
miliardi di numeri (dove la percantuale dei palindromi è 0,0011 % essendo 1099998 su 100 miliardi).
Il tempo di elaborazione è stato normalizzato di un fattore 85000 per rendere le due curve confrontabili sulla
stessa scala.
In realtà facendo un po’ di attenzione si può osservare che i palindromi sono simmetrici, siano essi composti
da un numero pari o dispari di cifre (es. 1991, 15951, ...) , quindi è sufficiente osservare le prime n cifre.
2
Notiamo che le prime n cifre crescono con continuità (es da 1000 a 10000 vanno da 10 a 99 -> abbiamo 90
2
palindromi):
numero
di cifre
numeri
palindromi
numero di pal fissato
numero di cifre
1
1
1
1
1
1
2
3
:
9
9
2
2
2
2
2
11
22
33
:
99
9
numero
di cifre
numeri
palindromi
numero di pal fissato
numero di cifre
3
3
3
3
3
3
3
3
3
3
3
101
:
191
202
:
292
:
:
909
:
999
90
4
4
4
4
4
4
4
4
4
4
4
1001
:
1991
2002
:
2992
:
:
9009
:
9999
90
E così via. Segue una tabella che riassume il numero di palindromi nell’insieme 10 m −1 ÷ 10 m con m>0 dove m
è il numero di cifre
dispari
pari
numero di cifre
1
2
3
4
5
6
…
2n-1
2n
numero di pal fissato
numero di cifre
9
9
90
90
900
900
…
...
...
9 ⋅ 10 0
9 ⋅ 10 0
9 ⋅ 101
9 ⋅ 101
9 ⋅ 10 2
9 ⋅ 10 2
…
9 ⋅ 10 n −1
9 ⋅ 10 n −1
Si nota che l’esponente del 10 cresce con una certa regolarità: per ogni numero di cifre pari il numero dei
palindromi è lo stesso del numero di cifre dispari immediatamente precedente. In tabella abbiamo introdotto il
generico numero pari 2n ed il generico numero dispari 2n-1 . Con la legge con cui crescono le potenze di 10,
considerato il numero di cifre che compongono l’estremo dell’insieme esaminato, abbiamo per il generico
numero pari 2n in totale 9 ⋅ 10 n −1 numeri palindromi (compresi tra 10 2 n e 10 2 n −1 ) e la stessa quantità per il generico
2 n −1
2n−2
e 10
):
numero dispari strettamente inferiore 2n-1 (compresi tra 10
In totale da 1 a 10 n , se n è il numero di cifre che consideriamo, avremo una sommatoria per
•
n pari
n −2 2
i
# pal = 18 ⋅ ∑10
i =0
•
numeri palindromi
n dispari
n 2−3
n −1
i
# pal = 18 ⋅ ∑10 + 9 ⋅ 10 2
i =0
numeri palindromi
La percentuale di palindromi per ogni insieme considerato (da 1 a 10 n , se n è il numero di cifre che consideriamo)
sarà data da:
pal % =
# pal
⋅ 100
10 n
e la frazione di palindromi sarà semplicemente
# pal
10 n
Ora l’andamento asintotico per n → ∞ sarà dettato dal rapporto tra le componenti di numeratore e
donominatore a esponente più alto, si ricava quindi
n
2
10
10 n
•
per n pari
•
10 2
per n dispari
10 n
n +1
siccome per n grande n ≅ n + 1 possiamo concludere che l’andamento asintotico sarà del tipo:
frazione palindromi → 10
−
n
2
queste previsioni sono in perfetto accordo con i dati ottenuti mediante il programma che effettuava il ciclo esaustivo,
vedi grafico seguente:
Diego Alberto, Novembre 2005












