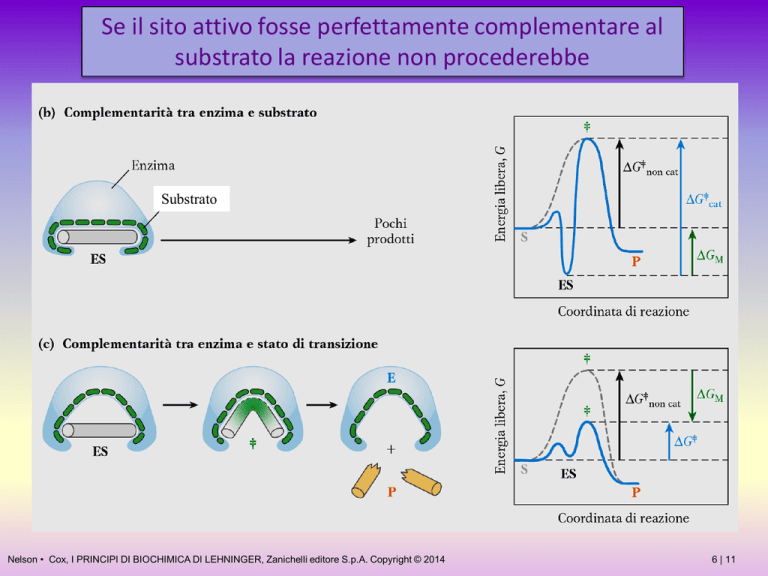
Se il sito attivo fosse perfettamente complementare al
substrato la reazione non procederebbe
Substrato
Nelson • Cox, I PRINCIPI DI BIOCHIMICA DI LEHNINGER, Zanichelli editore S.p.A. Copyright © 2014
6 | 11
La specificità del legame enzima/substrato può essere spiegata col modello
chiave-serratura di Fisher
Il sito attivo possiede
dei punti di ancoraggio
specifici per i gruppi
funzionali del
substrato
Il potere catalitico di un enzima può essere spiegato col modello
dell’adattamento indotto di Koshland
L’enzima ha un sito che può alloggiare in modo specifico un substrato
ma questo sito diventa
complementare al substrato
solo nello stato di transizione
e solo attraverso un
cambiamento conformazionale
dell’enzima stesso
Quando si forma il complesso ES nel distorcere il substrato l’enzima
stesso cambia conformazione adattando perfettamente la forma del
sito catalitico allo stato di transizione del substrato e presentando ad
esso i suoi gruppi catalitici.
esochinasi
(è una trasferasi: trasferisce sul C-6 del glucosio un gruppo
fosfato donato dall’ATP e produce glucosio-6-fosfato)
velocità di reazione
Effetto della temperatura sulla velocità
di una reazione enzimatica
La velocità di reazione aumenta
all’aumentare della temperatura sino a
raggiungere un valore massimo
(Mantenendo costanti pH, [E] e [S])
Optimum di temperatura: è
diverso per i diversi enzimi
A T° superiori a quella
ottimale:
- sono alterate le interazioni
che consentono la
formazione di ES;
- l’enzima va incontro a
modificazioni strutturali del
sito attivo (rottura dei legami
deboli, denaturazione)
Effetto del pH sulla velocità di una reazione enzimatica
Velocità di reazione
Da ricollegare al diverso stato di protonazione delle catene laterali di
residui amminoacidici che costituiscono il sito catalitico e il sito di
legame per il substrato.
velocità di reazione
Massima attività
His-159
Cys-25
Cys-25
His-159
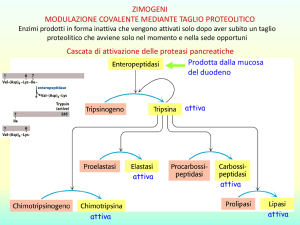
PAPAINA = enzima proteolitico, scinde
i legami peptidici delle proteine.
Nel sito attivo sono presenti una
cisteina molto acida e un’istidina
molto basica.
FORMANO UNA COPPIA IONICA
Cys-25
His-159
4
5
6
7
8
9
Massima attività: intervallo di pH
compreso fra i pKa di due residui
amminoacidici del sito attivo (fra pH
4.2 e 8.2). In questo intervallo le
catene laterali di entrambi i residui
amminoacidici sono ionizzati.
S¯
pH
C
O= l ―H
C
― l
HN
3
2
CH
l
2
O=C
l
C ―H
HN―
l
CH 2
H
l
+
C―N CH
C―N
H
H
His-159 (pKR 8.2)
Cys-25 (pKR 4.2)
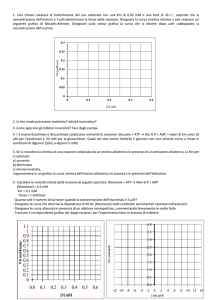
1) Perché studiare la cinetica di una reazione enzimatica?
Per determinare dei parametri specifici e caratterizzanti per un dato enzima che ci
dicono:
- Quanto un enzima è affine ad un dato substrato
- Quanto l’enzima è efficiente
- Come posso controllare la velocità della reazione
- Come posso regolare l’attività catalitica dell’enzima (inibendolo o attivandolo)
2) Cosa devo misurare per studiare la cinetica enzimatica?
LA VELOCITA’ DI REAZIONE AL TEMPO ZERO
IN FUNZIONE DELLA CONCENTRAZIONE DI SUBSTRATO
(misurata come variazione della concentrazione di prodotto ottenuto nel
tempo, o di substrato consumato nel tempo)
3) Come interpreto i dati ottenuti?
Applico delle equazioni matematiche.
Il modello matematico BASE per elaborare i dati di una cinetica enzimatica
(per enzimi non allosterici)
è quello proposto da L. Michaelis e M. Menten (1913)/Haldane e Briggs
(1925)
CINETICA ENZIMATICA
Gli esperimenti di cinetica enzimatica si basano sulla determinazione della velocità
di reazione, misurata come variazioni della concentrazione del prodotto o del
reagente in un dato intervallo di tempo.
[P] = aumenta nel tempo
[S]= diminuisce nel tempo
S→P
[S]
v = Δ[P]
Δt
=
[P]
_ Δ[S]
Δt
Col procedere della reazione le curve
cinetiche si appiattiscono: la velocità
non subisce variazioni. S è consumato
perché trasformato in P e la reazione
tenderà a raggiungere l’equilibrio.
tempo
S→P
v = Δ[P]
Δt
=
_ Δ[S]
Δt
[P] = aumenta nel tempo
[S]= diminuisce nel tempo
[P]
[S]
Problema:
Voglio misurare in che modo varia la velocità
della reazione se uso diverse concentrazioni
di substrato (1, 5, o 10 mM, per es…).
tempo
Devo misurare la velocità della reazione al MOMENTO INIZIALE (entro i primi 50-60
sec), quando la quantità di prodotto formato è molto bassa e la concentrazione del
substrato ha un valore preciso che conosco (quello iniziale stabilito dallo
sperimentatore).
In questo modo posso associare al valore di [S]
utilizzato un dato valore di V0 (velocità iniziale)
COME DETERMINO LA VELOCITA’ INIZIALE?
Studio di una reazione enzimatica semplice (1 solo substrato e 1 solo stadio
intermedio):
1) miscelo l’enzima con il suo substrato, lavoro a temperatura e pH costanti,
2) Preparo un certo numero di miscele di reazione in cui la [E] è inalterata, ma la
[S] è diversa: per ogni esperimento misuro come varia la velocità di reazione nel
tempo.
3) Velocità di reazione: misuro la concentrazione di prodotto che si formerà in
tempi diversi nelle diverse miscele di reazione.
La
velocità
di
all’aumentare della
substrato utilizzata.
v = Δ[P]
Δt
=
_ Δ[S]
Δt
v = k [S]
reazione
aumenta
concentrazione del
k = -1/Δt
(costante di velocità
specifica per ogni
reazione)
-Reazione di 1° ordine-
v = Δ[P]
Δt
=
_ Δ[S]
Δt
4) Calcolo il valore della velocità di reazione nello stadio iniziale (v 0) alle diverse [S].
VELOCITA’ INIZIALE (v0) è calcolata come pendenza della tangente alla curva cinetica.
Per ognuna delle curve cinetiche ottenute a diverse [S] viene calcolata la v0
(4)
v0 (3)
v0 (2)
v0 (1)
v0 = k [S] • La
Ogni punto rappresenta un
diverso esperimento, ed è
definito da due parametri:
v0 e [S]
v0 è direttamente proporzionale alla
concentrazione di reagente [S] usata per la reazione.
• Per gli enzimi che seguono la cinetica di MicaelisMenten la dipendenza della v0 dalla [S] è descritta da
una curva iperbolica
ENZIMI CHE SEGUONO LA CINETICA DI MICHAELIS-MENTEN
Alte [S] = la v0 non varia molto al
variare di [S], l’enzima è quasi
completamente
saturato,
viene
raggiunta asintoticamente una velocità
di reazione massima. La v0
non
dipende più da [S].
Basse [S] = la velocità di reazione v0
dipende strettamente dalla [S],
aumenta all’aumentare della [S]
Velocità iniziale v0 (μM/min)
Inserendo in un grafico i valori di v0 ottenuti per le diverse [S] utilizzate
ottengo una curva iperbolica
Concentrazione substrato [S] (mM)
Posso spiegare questo comportamento con un’equazione che
correla la v0 alla [S], alla Vmax e ad una costante di affinità (Km)
ENZIMI CHE SEGUONO LA CINETICA DI MICHAELIS-MENTEN
Mostrano una dipendenza della velocità iniziale (v0) dalla
concentrazione di substrato di tipo IPERBOLICO.
Catalizzano una reazione enzimatica che nel caso più semplice prevede:
1 prima tappa veloce e reversibile (ΔG‡ minore e k maggiore)
k1
S+E
k-1
ES
1 seconda tappa lenta e irreversibile (ΔG‡ maggiore e k minore) che
determina la velocità globale di reazione
ES
k2
k-2
E+P
k1 = cost cinetica reazione di formazione del complesso ES
k-1 = cost cinetica reazione di decomposizione del complesso ES in E + S
k2 = cost cinetica reazione di decomposizione del complesso ES in E + P
k-2 = talmente piccola da essere trascurabile
v = k2 [ES]
v = k1 [E] + [S]
1a tappa:
Passaggio rapido
S+E
k1
k-1
ES
k2
E+P
v = k-1 [ES]
2a tappa: Passaggio lento
La v0 GLOBALE della reazione
enzimatica dipende da [ES]
Questa equazione non è sufficiente a spiegare
la relazione iperbolica esistente tra v0 e [S].
v0 = k2 [ES]
[ES] = non è facilmente
misurabile, e k2 non è nota
Bisogna ricavare un’equazione alternativa partendo dalla
considerazione che la [ES] rimane costante nel tempo della reazione,
k1
e che la 1a tappa della reazione enzimatica
S+E
ES
k-1
raggiunge rapidamente lo STATO STAZIONARIO
COMPLESSIVAMENTE [ES] RIMANE COSTANTE NEL TEMPO
La concentrazione dell’enzima libero
[E] in soluzione diminuisce man
mano che aumenta la concentrazione
del complesso [ES].
Ma poiché il complesso ES è
demolito continuamente (in E + S o in
E + P), l’ENZIMA è di nuovo reso
libero.
STATO STAZIONARIO
[ES] rimane costante: la velocità della sua formazione è uguale
alla velocità della sua demolizione
S+E
k1
k-1
ES
k2
Velocità di Formazione di ES
(E + S → ES):
V = k1 [E] [S] = k1 ([E]TOT—[ES]) [S]
E+P
Velocità di Demolizione di ES
(ES → S + E …..ES → P + E):
V = k-1 [ES] + k2 [ES]
[E] = [E]TOT – [ES] poiché la concentrazione TOTALE di Enzima è [E]TOT = [E] + [ES]
Se è raggiunto lo stato
V formazione ES = V demolizione ES
stazionario posso dire che: k ([E] —[ES]) [S] = k [ES] + k [ES]
1
TOT
-1
2
Riarrangiando l’equazione tramite operazioni algebriche si ottiene che:
([E]TOT — [ES]) [S] = ( k-1 + k2)
[ES]
k1
k-1 + k2
Km =
k1
Costante di
Michaelis-Menten
k-1 + k2
Km =
k1
Costante di
Michaelis-Menten
Il rapporto fra le costanti cinetiche della
dissociazione di ES e quella della sua
formazione è uguale alla COSTANTE DI
DISSOCIAZIONE DEL COMPLESSO ES
Semplificando i termini dell’equazione precedente si ottiene che:
Poiché la v0 globale v = k [ES] e quindi:
0
2
di reazione è :
[ES] = v / k
0
2
k2[E]TOT [S]
v0 =
[S] + Km
[E]TOT [S]
[ES] =
[S] + Km
k2[E]TOT [S]
v0 =
k2 [E]TOT = Vmax
[S] + Km
Introduciamo un altro parametro importante: la Velocità massima di reazione.
Quando sono presenti nella miscela di reazione concentrazioni saturanti di
substrato, allora, tutto l’enzima è complessato col substrato e la [E]TOT = [ES]
La velocità globale di reazione non dipende più dalla concentrazione di
substrato, ma solo dalla concentrazione totale dell’enzima:
v0 = k2 [ES] diventa Vmax = k2 [E]TOT
Vmax [S]
EQUAZIONE DI MICHAELIS-MENTEN
v0 =
[S] + Km
Equazione di Michaelis-Menten
S+E
v0 =
Km + [S]
La velocità iniziale della reazione
enzimatica dipende dalla [S] in modo
iperbolico ed è correlata alla
Vmax (= k2[E]tot) e alla Km
Il valore della Km si può determinare
sperimentalmente = Corrisponde alla
[S] alla quale raggiungo la metà della
Vmax. Ha le unità di misura di una
concentrazione
Vmax [S]
v0 = ½ Vmax
1
[S] + Km
2
ES
E+P
[S] (mM)
[S]
=
=
k-1
k2
v0 (μM/min)
Vmax [S]
k1
[S] + Km
Km + [S] = 2 [S]
Km = [S]
Solo se v0 = ½ Vmax
Km =
k-1+ k2
k1
(k2 << k-1 = trascurabile)
Km =
k-1
k1
La Km è uguale alla costante di
dissociazione del complesso ES
La Km fornisce informazioni sull’affinità che un enzima ha nei confronti
del suo substrato ed è SPECIFICA per ogni diverso enzima nei confronti
di un dato substrato.
Più è grande, minore sarà l’affinità dell’enzima per il substrato
(maggiore sarà la costante di dissociazione del complesso ES, k-1 > k1)
Più è piccola maggiore sarà l’affinità (minore la costante di
dissociazione di ES, k1 > k-1)
Considerazioni valide per reazioni enzimatiche semplici a due tappe e in cui k2 << k-1,
non per tutti gli enzimi, molte reazioni enzimatiche sono a più tappe e la Km diventa
una funzione più complessa che dipende da varie costanti cinetiche.
La Km fornisce informazioni sulla efficienza della catalisi e sul controllo della velocità
se [S] >> 10 Km → concentrazioni saturanti di substrato, la reazione è molto efficiente
perché quasi a Vmax, ma non controllabile variando la [S]
se [S] << 0.1 Km → concentrazioni bassissime di substrato, la reazione non è efficiente
ma la si può controllare variando [S], poiché la v0 aumenta all’aumentare della [S].
[S] >> 10 Km
Nelle cellule [S] ≈ Km
→ la reazione ha velocità
intermedia ed è
regolabile variando [S]
[S] << 0.1 Km
Berg et al., BIOCHIMICA 6/E, Zanichelli editore S.p.A. Copyright © 2007
v0 (μM/min)
1 enzima
2 substrati simili A e B
medesime condizioni di reazione
Verso quale dei due l’enzima è più affine?
A
B
½ Vmax
KmA
KmB
[S] mM
A
Costante catalitica o n° di Turnover
S+E
k1
k-1
ES
k2
E+P
Vmax = k2 [ES] = k2 [E]TOT
k2 =
Vmax
[E]TOT
k2 per una reazione semplice ad uno stadio
corrisponde alla kcat (costante catalitica)
Indica il numero di eventi catalitici che avvengono nel sito attivo
dell’enzima nell’unità di tempo (le sue unità di misura sono s-1 o min-1).
Misura quanto velocemente un dato enzima può catalizzare una data
reazione. E’ SPECIFICA per ogni enzima.
Se lavoro con una miscela di reazione enzimatica in cui utilizzo una
[S] saturante e voglio raddoppiare la velocità di reazione cosa devo
modificare nella miscela di reazione? In che modo?
A [S] saturante la v0 raggiunge il suo valore massimo (Vmax), non può più variare in
funzione della concentrazione di substrato, perché tutto l’enzima presente è
saturato. Se voglio aumentare la Velocità di reazione devo aggiungere altro enzima
alla miscela di reazione.
Vmax = k2 [E]tot
v0 (μM/sec)
per raddoppiare la velocità di reazione (Vmax)
devo raddoppiare la concentrazione dell’enzima
VmaxB = k2 [E]B
[E]B = 2 [E]A
Vmax A = k2 [E]A
LA Km RIMANE INVARIATA
Km
[S] mM
EFFICIENZA CATALITICA DI UN ENZIMA
Costante di specificità:
kcat/Km (M-1sec-1)
ENZIMA
Parametro che utilizziamo per confrontare
l’efficienza catalitica e la specificità di enzimi
diversi per uno stesso substrato o di uno
stesso enzima per substrati diversi.
SUBSTRATO
kcat
(sec-1)
Km
(M)
kcat/Km
(M-1sec-1)
Acetilcolinesterasi Acetilcolina
1.4x104
9x10-5
1.6x108
Anidrasi carbonica CO2
1x106
1.2x10-2
8.3x107
Anidrasi carbonica HCO3-
4x105
2.6x10-2
1.5x107
Catalasi
H2O
1.4x104
9x10-5
1.6x108
Fumarasi
Fumarato
8x102
5x10-6
1.6x108
Fumarasi
Malato
9x102
2.5x10-5
3.6x107
In reazioni più complesse a più stadi: la kcat corrisponderà alla k2 dello stadio
limitante la velocità della reazione complessiva
Oppure in situazioni più complesse sarà uguale alla combinazione di molte costanti di
velocità diverse
Es: reazione multistadio e
multisubstrato a PING PONG
Nelson • Cox, I PRINCIPI DI BIOCHIMICA DI LEHNINGER, Zanichelli editore S.p.A. Copyright © 2014
6 | 36
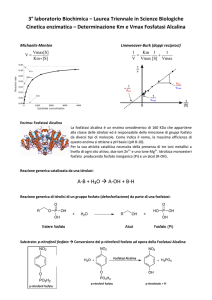
Determinazione sperimentale di Km e Vmax per una reazione enzimatica:
GRAFICO DEI DOPPI RECIPROCI (Eq. di Lineweaver-Burk)
(linearizzazione della curva iperbolica) >>>>
1
v0
=
Km
1
1
+
Vmax [S] Vmax
La curva iperbolica del
grafico di MicaelisMenten diventa una retta
che interseca gli assi in
punti precisi consentendo
di determinare con
esattezza Km e Vmax, e
quindi anche kcat
1/v0 min/μM
I valori sperimentali di v0 sono trasformati nei loro reciproci: 1/v0
e i valori sperimentali di [S] nei corrispettivi reciproci 1/[S]
Pendenza della retta
= Km/Vmax
1/v0 = 1/Vmax
[S] = 10 mM
-1/Km
0,1
1/[S] mM-1
[S] =
1,0 mM
1,0
1/v0 min/μM
Per calcolare la Vmax devo fare il reciproco
del reciproco =
1 = 0,02 min/μM → Vmax =
1
Vmax
0,02 min/ μM
Vmax = 50 μM/min
1/Vmax
= 0,02
[S] = 1,0 mM
[S] = 10 mM
v0 (μM/min)
-0,5 = -1/Km
0,1
1/[S] mM-1
1,0
Per calcolare il valore della Km devo fare il
reciproco negativo del reciproco =
-1/Km = -0,5 mM-1 → Km = - 1
= 2mM
-0,5 mM-1
1
Km
v0 = Vmax
Vmax 50 μM/min
Vmax
2
v0 =
2,0 (Km)
[S] mM
1
1
[S] + Vmax
Vmax [S]
Km + [S]