Esercizi di fisica sui vettori
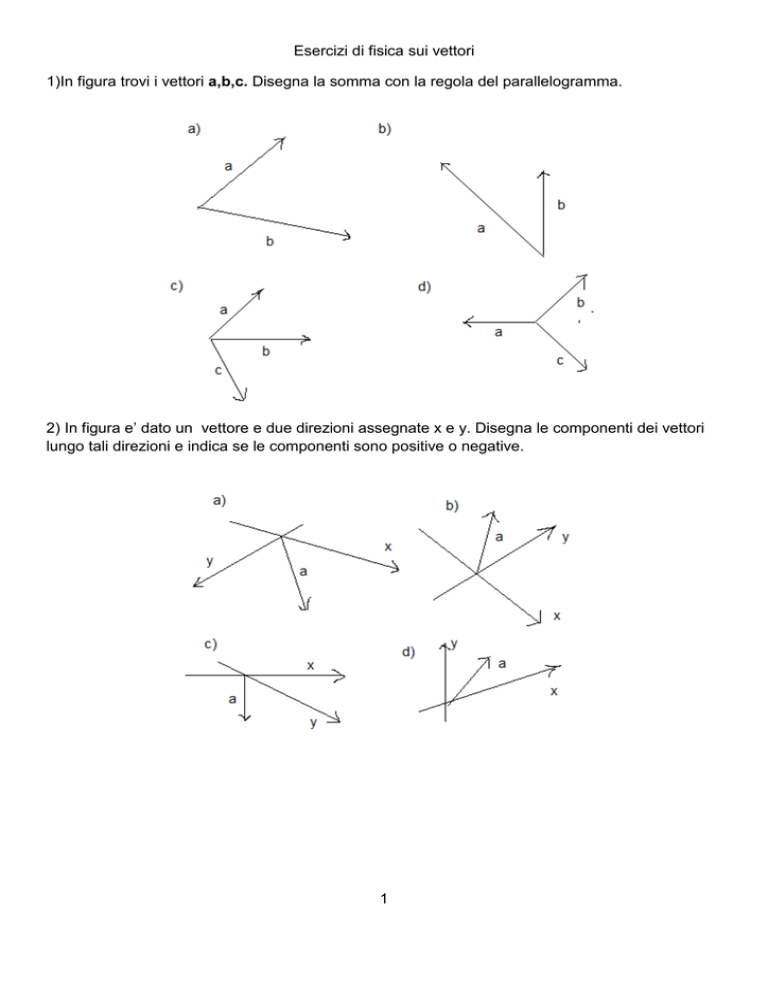
1)In figura trovi i vettori a,b,c. Disegna la somma con la regola del parallelogramma.
2) In figura e’ dato un vettore e due direzioni assegnate x e y. Disegna le componenti dei vettori
lungo tali direzioni e indica se le componenti sono positive o negative.
1
3) In figura trovi dei triangoli rettangoli con le misure indicate. Calcola angoli e i lati rimanenti.
4)In figura trovi dei vettori e gli angoli indicati.
a)Calcola le componenti e disegnale con la massima attenzione.
b)Scrivi i vettori in forma analitica.
5)In figura trovi tre vettori v,w,z.
a)Disegna le componenti e valutane le intensità’.
b)Scrivi i vettori in forma analitica;
c)Calcola l’intensità’ e la direzione (cioè l’angolo che il vettore
forma con l’asse delle ascisse) dei vettori:
1)S=v+w+z;
2)T=v-w-z;
3)H=v+w-z;
4)X=2v-3w+z
2
d)Detto A l’estremo del vettore v(3;5), B l’estremo di w(4;-3); C l’estremo di t(-2;2), scrivi i vettori
AB, BC, AC.
e)calcola il prodotto scalare e vettoriale dei vettori OA e OB, OB e OC, AB e BC
f)Calcola l’area dei triangoli OAB, OAC, OBC.
g) Calcola l’angolo tra i vettori AB e OA e tra AB e OB.
6)In figura trovi i vettori v,w,z. v=5; w=5; z=5.
a)Calcola l’intensità’ e la direzione dei vettori:
S=w+v;
T=w-v;
G=z-w
b)Scrivi i vettori in forma analitica
c)Indica con A l’estremo di v, con B l’estremo di z e con C l’estremo di w. Scrivi i vettori AB,AC,BC
e calcola tutti gli angoli del triangolo ABC.
→
→
7)In figura trovi due vettori a e b .
→
→
→
a)Calcola il modulo del vettore somma e della differenza d = a − b .
b)Rappresenta graficamente i vettori trovati e verifica il risultato con
la regola del parallelogramma.
c) Scrivi i vettori in forma analitica;
d)Calcola il prodotto vettoriale e scalare;
e)Se unisci gli estremi dei due vettori ottieni un triangolo OAB dove A e’ l’estremo del vettore a e B
e’ l’estremo di b. Scrivi il vettore AB e calcola l’area del triangolo OAB.
8)In figura trovi i vettori v e w. (V=5 e w=10)
a)Scrivi i vettori in forma analitica ;
b)calcola la somma S=v+w, la differenza D= w-v e la differenza
G=v-w.
c)Rappresenta graficamente i vettori trovati;
d)Calcola il prodotto scalare e vettoriale;
e) Se unisci gli estremi dei due vettori ottieni un triangolo OVW dove V e’ l’estremo del vettore v e
W e’ l’estremo di w.. Scrivi il vettore WV e calcola l’area del triangolo OVW
3
9)In figura trovi dei vettori.
a)Disegnali in scala e con la regola del poligono funicolare
costruisci il il vettore somma.
→
→
→
→
→
→
b)Disegna i vettori differenza: d = a − b e f = a − c
c)Scrivi i vettori in forma analitica e calcola il modulo del vettore somma e la direzione;
d)Calcola il prodotto scalare e vettoriale tra i vettori a e b, c e d.
10)In figura trovi dei vettori: (a=4cm e b=2cm)
a)Calcola le componenti di ciascun vettore e
disegnale con cura;
b)Scrivi i vettori in forma analitica e calcola il
modulo e la direzione del vettore somma e
differenza
c)Calcola il prodotto scalare e vettoriale
d)Indica con A e B i punti estremi dei vettori e
calcola l’area del triangolo OAB.
e)Scrivi in forma analitica il vettore AB.
f)Calcola gli angoli interni del triangolo OAB
11) Scrivi in forma analitica i vettori v(4;-3) e w=(5;12) e calcola il prodotto scalare. Calcola
l’angolo formato dai due vettori.
R:(vxw=-16; angolo=1,819 rad)
12) Dire per quali valori di k l’angolo tra i seguenti vettori e’ di π/3: v(k;1), w(1;-2). R: -8±rad(5)
13) I vettori a e b hanno moduli a = 6,82 e b = 9,47 e formano tra loro un angolo di 45°. Quanto
vale il prodotto scalare a x b ? [45,7]
14) Il vettore u è rivolto verso Est mentre il vettore v forma con u un angolo di 60° in senso
antiorario (cioè verso Nord). I loro moduli sono u = 15 e v = 12. Determina l’intensità, la direzione
e il verso del vettore w prodotto vettoriale [1,6 x 102 unità]
15)I vettori a e b costituiscono rispettivamente l’ipotenusa e un cateto di un triangolo rettangolo. Il
modulo di a vale 10,0 unità e l’altro cateto del triangolo è lungo 5,0 unità. Calcola:
a)l’ampiezza dell’angolo formato dalle direzioni dei due vettori;
b)il modulo del vettore b ;
c)il modulo del prodotto vettoriale tra a e b .
[30°; 8,7 unità; 44 unità]
4
16)I vettori d ed e hanno moduli d = 5,39 ed e= 4,65 e formano tra loro un angolo di 120°.
Quanto vale il prodotto scalare tra d ed e?
[12,5]
17)Considera un vettore a e altri cinque vettori b, c , d, e , f , di modulo uguale ad a, orientati
rispetto ad a nel seguente modo: b è parallelo ad a con lo stesso verso, c è parallelo ad a ma
con verso opposto, d è perpendicolare ad a, e è inclinato di 30° rispetto ad a e f è inclinato di 120°
rispetto ad a. Ordina, dal più piccolo al più grande, i valori dei prodotti scalari di a con i cinque
vettori elencati.
5












