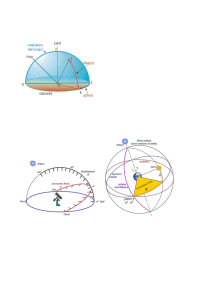
1 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 I sistemi di coordinate spazio-­‐temporali in astrofisica. L’immagine del cielo che ci viene offerta dall’osservazione è bidimensionale, proiettata su una superficie sferica di grandi dimensioni con l’osservatore terrestre posto al centro. Le stelle appaiono tutte alla stessa distanza, senza alcun effetto di prospettiva: durante la notte descrivono sulla sfera delle traiettorie curve, sorgendo dall’orizzonte a est, salendo fino a un’altezza massima (culminazione1) e tramontando verso ovest. Questa rappresentazione è ovviamente apparente e non completa: gli oggetti celesti sono distribuiti in uno spazio tridimensionale, la mancanza di prospettiva è semplicemente dovuta alla loro enorme distanza dalla Terra, tanto che all’osservatore terrestre appaiono tutti "all’infinito". Tuttavia per riconoscere la direzione in cielo in cui individuare gli astri e per descriverne i moti apparenti diurni e annui è sufficiente fare riferimento alla descrizione bidimensionale. La superficie su cui si vedono proiettati gli astri è chiamata sfera celeste. Per individuare la posizione di un astro nel cielo è necessario definire un sistema di coordinate2. In tal modo, nota la posizione di un oggetto celeste e scelto un adeguato sistema di riferimento, un osservatore posto in un punto qualsiasi della superficie terrestre sarà in grado di individuarlo. Visto che nella realtà gli astri hanno distanze diverse dalla Terra, le coordinate celesti individuano una direzione orientata, ossia una semiretta originata nell'osservatore e passante per l'astro. Le tecniche per definire quantitativamente e con grande precisione posizioni e moti degli astri fanno parte dei capitoli dell’astronomia chiamati astronomia fondamentale e astrometria. In astronomia il sistema di coordinate non è unico3. Ciascun sistema presenta vantaggi evidenti per un determinato tipo di problema; la scelta di un sistema piuttosto che di un altro è determinata dal tipo di oggetti che si studiano. 1.1 Il sistema dell’orizzonte o alt-­azimutale. Le coordinate altazimutali, chiamate anche coordinate orizzontali, sono coordinate locali: questo è il sistema di riferimento più naturale per un osservatore terrestre perché è legato all’ambiente circostante. La posizione di un astro in cielo può essere individuata dalla sua elevazione sull’orizzonte e dalla sua direzione relativamente a quelli che chiamiamo i punti cardinali locali. Prendiamo come piano di riferimento il piano tangente alla superficie terrestre nel punto di osservazione; esso interseca la sfera celeste lungo l’orizzonte. Chiamiamo zenit il punto della sfera celeste che si trova esattamente sopra l’osservatore e nadir quello diametralmente opposto. I cerchi massimi4 che passano per zenit e nadir sono detti cerchi verticali (o verticali), perché intersecano perpendicolarmente l’orizzonte; il cerchio verticale a cui tutti gli astri culminano è chiamato cerchio meridiano o meridiano locale e individua sull’orizzonte le direzioni del sud e del nord. 1
Si dice transito al meridiano o culminazione, il punto più alto sull'orizzonte visivo raggiunto da un astro nel suo moto da est a ovest sulla volta celeste. 2
Le coordinate possono essere cartesiane (x, y, z) o polari (la distanza e due angoli); il primo sistema può essere comodo nei calcoli ma è inadatto alla registrazione dei dati; in Astronomia si usano dunque solo coordinate polari: la distanza e due angoli. 3
Nella pratica i due sistemi più usati sono quello equatoriale e quello galattico; opportune formule di trigonometria sferica permettono di passare dalle coordinate in un sistema a quelle in un altro. 4
Un cerchio massimo è una circonferenza che divide la sfera celeste in due identiche semisfere. Coordinate astronomiche – Ilaria De Angelis 2 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 Figura 1. Il sistema altazimutale definisce un punto sulla sfera celeste grazie a due coordinate: l'altezza (h) e l'azimut (A). Come riferimenti si prendono: l'orizzonte (la circonferenza massima che separa l'emisfero celeste visibile da quello non visibile) e il meridiano locale (la circonferenza massima passante per lo zenit dell'osservatore e per i poli, che incontra l'orizzonte nei punti Nord e Sud). Le coordinate angolari usate per definire la posizione sulla sfera celeste di un astro sono: •
•
l’altezza : l’angolo, misurato lungo il verticale che passa per l’oggetto, tra l’orizzonte e l’astro; l’azimut : l’angolo, misurato lungo l’orizzonte, tra il verticale dell’oggetto e un verticale fisso prescelto. L’altezza varia tra -­‐90°e +90° ed è positiva per posizioni al di sopra dell’orizzonte (per lo zenit ) e negativa al di sotto dell’orizzonte (per il nadir ). A volte al posto dell’altezza si usa la distanza zenitale , cioè la distanza angolare dell'astro dallo zenit dell'osservatore, ovvero l’angolo h, che varia da 0° a 180°. Il verticale fisso a partire da cui si misura l’azimut è il meridiano locale e gli angoli sono misurati da nord5 in senso orario (quindi verso est) da 0°a 360°. Sebbene semplice da definire, il sistema altazimutale è difficile da usare nella pratica. Le coordinate celesti di un oggetto sono infatti specifiche della latitudine e della longitudine dell’osservatore e sono difficili da trasformare per altre località. Inoltre, poiché la Terra ruota, le stelle sembrano muoversi costantemente, e quindi le coordinate di un oggetto cambiano in continuazione, anche per l’osservatore locale. A complicare ulteriormente il problema c’è il fatto che ogni stella sorge (approssimativamente) 4 minuti prima col passare delle notti, così che anche quando si osserva dalla stessa località a un tempo fissato, le coordinate cambiano di giorno in giorno. Queste coordinate non possono essere quindi alla base di un catalogo celeste generale. 1.1.1 Tempo siderale e tempo solare Per capire il problema di questi cambiamenti quotidiani delle coordinate altazimutali, dobbiamo considerare il moto della Terra intorno al Sole. Mentre la Terra percorre la sua orbita, la nostra visione delle stelle distanti cambia costantemente: guardando in direzione del Sole, la nostra linea di vista incontra costellazioni diverse col cambiare delle stagioni; di conseguenza vediamo il Sole muoversi apparentemente attraverso queste costellazioni (per esempio, durante la primavera il Sole sembra muoversi nella costellazione dell’Ariete, in autunno nella Bilancia) lungo un cammino chiamato 5
Alcuni lo misurano a partire da sud. Coordinate astronomiche – Ilaria De Angelis 3 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 eclittica6. Di conseguenza queste costellazioni sono cancellate dalla luce del giorno e altre appaiono nel cielo notturno. Questo cambiamento stagionale nelle costellazioni è legato al fatto che una data stella sorge circa 4 minuti prima ogni giorno. Il periodo siderale è il tempo che impiega la Terra per compiere un'intera orbita intorno al Sole, ovvero il tempo impiegato per ritornare allo stesso punto rispetto alle stelle fisse. La Terra completa un periodo siderale in 365.26 giorni, quindi percorre poco meno di 1° in 24 ore. Perciò la Terra deve ruotare di 361°affinché il Sole torni al meridiano locale il giorno seguente (come si vede in figura), mentre bastano 360° nel caso delle stelle che non cambiano significativamente la loro posizione visto che sono molto più distanti dalla Terra rispetto al Sole. Occorrono circa 4 minuti alla Terra per ruotare di questo grado extra, quindi una data stella sorge 4 minuti prima ogni notte. Definiamo quindi giorno solare l’intervallo medio di 24 ore tra 2 passaggi consecutivi del Sole al meridiano locale e giorno siderale l’intervallo tra 2 passaggi consecutivi di una stella. 1.2 Il sistema equatoriale. Il sistema equatoriale è basato sul sistema latitudine-­‐longitudine della Terra, ma non è soggetto alla rotazione del pianeta; non dipende dalla posizione dell’osservatore sulla superficie terrestre né dal moto della Terra intorno al Sole e quindi viene spesso usato per mappe e cataloghi stellari. In analogia con le coordinate usate per definire la posizione sulla superficie della Terra, anche per la sfera celeste si utilizzano latitudini e longitudini; in pratica occorre individuare l’equivalente di un equatore (o di due poli) e di un meridiano zero. Si dovrà cioè individuare un piano che passi per il centro della sfera celeste e la intersechi in un cerchio massimo che la divide in due emisferi (l’analogo dell’equatore terrestre), e su questo un punto origine (l’analogo dell’intersezione dell’equatore terrestre con il meridiano di Greenwich). Una delle coordinate indicherà la distanza angolare da questo piano (latitudine); la seconda coordinata (longitudine) sarà la distanza angolare tra i piani meridiani, perpendicolari all’equatore, passanti uno per l’oggetto considerato e l’altro per un punto fisso sull’equatore (il punto origine scelto). 6
L’eclittica è l’intersezione del piano che contiene l’orbita della Terra attorno al Sole con la sfera celeste: visto dal punto di vista terrestre è la traiettoria apparente che il Sole sembra compiere nel corso di un anno. Coordinate astronomiche – Ilaria De Angelis 4 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 La prima linea da riportare sarà l'equatore terrestre che, virtualmente espanso e trasferito in cielo, diviene l'equatore celeste. Insieme ad esso trasferiremo tutti gli altri paralleli, i quali andranno a coprire tutti i circoli minori della sfera celeste, cioè tutte le latitudini celesti (per così dire) dal Polo Nord Celeste, indicato dalla stella Polare, sino al Polo Sud Celeste. Poi riporteremo sulla sfera celeste la proiezione del meridiano passante per il nostro luogo di osservazione, generando in cielo il meridiano locale, e con esso tutti gli altri meridiani che andranno a formare la seconda coordinata, una sorta di longitudine celeste. Definiamo piano equatoriale il piano che interseca la sfera celeste nell’equatore celeste. Tale piano è inclinato rispetto a quello dell’orbita terrestre e quindi l’eclittica e l’equatore si intersecano in due punti detti punti equinoziali. Di questi due punti viene preso come riferimento7 l’equinozio di primavera (il punto dove il Sole attraversa ogni anno l'equatore celeste da Sud verso Nord), detto Punto Gamma γ (o Primo punto d'Ariete8 o Punto vernale). L’estensione dell’asse terrestre interseca la sfera nei poli celesti nord e sud, per cui è anche detto asse polare. La Stella Polare si trova attualmente a circa 40’ dalla posizione del polo nord. Tutti i piani passanti per l’asse polare, detti piani meridiani, intersecano normalmente l’equatore e disegnano i cerchi meridiani sulla volta celeste. L’angolo di elevazione di un astro rispetto all’equatore si chiama declinazione δ (è l’analogo della latitudine) e non cambia durante il moto diurno perché questo moto è sempre una traiettoria circolare intorno al polo. Il Sole cambia la propria declinazione tra (solstizio d’inverno) e (solstizio d’estate) con periodo annuale; grazie a questo abbiamo le stagioni. La seconda coordinata del sistema è chiamata ascensione retta α oppure R.A. (l’analogo della longitudine) ed è l’angolo tra il Punto γ e il piede dell’astro9. L’ascensione retta è espressa10 in ore (h), minuti (m) e secondi (s) in un cerchio di 24 ore (che corrispondono a 360° o, analogamente, 1 ora = 7
Poiché abbiamo bisogno di un punto di riferimento certo nella sfera celeste, non possiamo semplicemente proiettare il Meridiano Zero di Greenwich per avere un riferimento. Quest'ultimo, infatti, a causa della rotazione terrestre non sarebbe fisso. Al suo posto si utilizza invece il Punto Gamma. 8
Chiamato così perché originariamente era un punto nella costellazione dell’Ariete, ma si muove lungo l’intero equatore con periodo di 26.000 anni per effetto della precessione degli equinozi. 9
Il piede dell’astro è il punto d’intersezione del piano meridiano su cui si trova l’astro con l’equatore. 10
È più conveniente utilizzare le ore, i minuti ed i secondi anziché i gradi (come per la latitudine terrestre) perché questa divisione corrisponde al giorno siderale. Coordinate astronomiche – Ilaria De Angelis 5 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 15°) lungo l'equatore celeste e si misura in verso antiorario. La differenza di ascensione retta fra due astri definisce sia la distanza angolare fra i due astri rispetto all'equatore celeste, sia il tempo siderale che intercorre fra il presentarsi al meridiano locale del primo e del secondo astro. Si noti però che la distanza angolare dipende dalla declinazione! Infatti oggetti con la stessa separazione in ascensione retta hanno separazioni angolari diverse in funzione della declinazione. I 15° per 1h valgono solo per δ =0, cioè rispetto all’equatore. Si consiglia come esercizio: calcolare la separazione angolare tra due oggetti, date le rispettive coordinate (per questo occorre ricordare – o ricavare -­‐ una formula di trigonometria sferica). Puntando il telescopio (senza alcun motore guida), ad una coordinata, per esempio α = 0 h, δ =0°, e tornando dopo un'ora, potremo notare che il nostro strumento starà puntando a α = 1h, δ = 0°. Inoltre, puntando il telescopio sempre al punto con α = 0 h e δ =0°, 24 ore dopo il telescopio punterà a α = 0 h 4m e δ =0° a causa della differenza tra giorno solare e giorno siderale. La conseguenza è che le stelle che stiamo osservando sembrano levarsi quattro minuti prima ogni giorno che passa. Montando il nostro telescopio in modo tale che il suo asse di rotazione sia perpendicolare all’equatore, possiamo correggere il moto apparente delle stelle lungo la sfera celeste tramite una sola rotazione. Sebbene a prima vista sembri complesso, il sistema di coordinate equatoriali presenta molti vantaggi, rispetto a quello altazimutale: L'ascensione retta dell'astro resta immutata, infatti, al ruotare della sfera celeste, la distanza dell'astro dal Punto Gamma non cambia perché è la Terra a ruotare e, dal nostro punto di vista, insieme alla volta celeste girano sia l'astro sia la direzione del punto gamma. La declinazione δ non cambia perché la traiettoria della stella nel suo moto apparente è un arco di cerchio parallelo all’equatore celeste. Proprio per questa caratteristica, un corpo celeste con declinazione di +60° e ascensione retta di 4h 5m possiede queste coordinate sempre, anche se noi lo vediamo muoversi a causa della rotazione terrestre. Cosa non trascurabile, declinazione ed ascensione retta non variano se l’osservatore si sposta da un luogo all’altro della Terra, in quanto per la loro definizione non si sono utilizzati punti o cerchi di riferimento locali. Bisogna ricordare che c’è un problema nell’uso delle coordinate equatoriali: a causa della precessione, infatti, la posizione dell’oggetto cambia nel tempo, seppur molto lentamente, imponendo al necessità di correggere la posizione degli astri osservati. A causa dei movimenti a lungo termine della Terra (primo fra tutti quello conosciuto col nome di precessione degli equinozi), gli astri non hanno coordinate celesti del fisse ma variabili col tempo. Questo movimento è indipendente dal moto proprio delle stelle, perché si tratta di un movimento dell’osservatore piuttosto che dell’astro. Ad occhio nudo e su scale di pochi anni è impercettibile, ma per le osservazioni astronomiche si pone il problema di specificare a quale istante una coordinata si Coordinate astronomiche – Ilaria De Angelis 6 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 riferisce. È stato perciò inventato il concetto di epoca11: tutte le coordinate si specificano rispetto ad un’epoca, ed esistono algoritmi per passare da un’epoca all’altra. Nonostante l’entità dello spostamento possa apparire irrisoria su brevi periodi, su una scala di tempo di millenni esso può portare a notevoli variazioni nelle posizioni degli astri; ad esempio, tra circa 13000 anni il polo nord celeste sarà indicato da Vega, e non più dalla Stella Polare. Per una convenzione internazionale attualmente l’epoca di riferimento è l’equinozio del 2000: per esempio, le coordinate del polo nord Galattico (
) sono (
) e il punto (l ) corrisponde a (
trova a (
). Si noti che il centro della Galassia si ), quindi è molto vicino a (l ), ma non perfettamente allineato. 1.3 Il sistema di coordinate Galattiche. Il piano Galattico non è allineato con il piano dell’equatore celeste, ma è inclinato di un angolo di 62,6° rispetto ad esso. È conveniente quindi introdurre un nuovo sistema di coordinate per lo studio della Via Lattea e delle galassie esterne alla nostra. Il sistema di coordinate Galattiche sfrutta la naturale simmetria introdotta dall’esistenza del disco Galattico. L’intersezione del piano parallelo al disco della Galassia passante per il centro del Sole con la sfera celeste individua l’equatore Galattico. La latitudine Galattica b si misura in gradi nord o sud rispetto all’equatore Galattico lungo il cerchio massimo passante per il polo nord Galattico (NGP). La longitudine Galattica l si misura lungo l’equatore Galattico in verso antiorario a partire dal centro Galattico. 1.4 Altri sistemi di coordinate (cenni) 1.4.1 Sistema di coordinate eclittiche Un sistema di riferimento usato in passato è stato quello delle coordinate eclittiche, il cui cerchio massimo è l’eclittica, cioè la traiettoria apparente annua del Sole. Il sistema è utile per descrivere i moti dei corpi del sistema solare. In tale sistema l’equatore celeste è inclinato di un angolo fisso di 11
In astronomia, un'epoca è un istante a cui sono riferite alcune coordinate celesti o alcuni elementi orbitali. Poiché tutti gli oggetti celesti, Terra compresa, non sono fermi ma in movimento, una certa coordinata è valida solo per un certo istante. Coordinate astronomiche – Ilaria De Angelis 7 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 circa 23°27’, detto inclinazione dell’eclittica. Le coordinate del sistema sono la latitudine eclittica β, distanza angolare dal piano dell’eclittica, e la longitudine eclittica λ, misurata in verso antiorario a partire dal punto γ. 1.4.2 Sistema di coordinate supergalattiche Le galassie vicine non sono distribuite uniformemente nello spazio, ma sono organizzate in strutture, dai gruppi di alcune decine di galassie, agli ammassi di centinaia o migliaia di galassie, fino alla rete dei superammassi, detta struttura a grande scala dell'Universo. Se tracciamo la posizione delle galassie più brillanti (e quindi più vicine) sul cielo, notiamo una distribuzione molto disomogenea, con grosse concentrazioni di galassie, specialmente in corrispondenza del cosiddetto ammasso della Vergine. Le galassie vicine tendono a disporsi su una configurazione appiattita, detta piano supergalattico. Per lo studio della distribuzione delle galassie su grande scala è spesso usato il sistema delle coordinate supergalattiche, in cui il cerchio massimo è definito dal piano supergalattico. Le coordinate sono la longitudine supergalattica SGL e la latitudine supergalattica SGB in analogia alle coordinate galattiche, dove il punto zero della longitudine è dato dall’intersezione tra i piani galattico e supergalattico. 1.5 Perturbazioni e variazioni delle coordinate Vari effetti dinamici e atmosferici influenzano la misura delle coordinate degli astri e comportano una continua revisione dei cataloghi. Questi effetti sono essenzialmente dovuti al fatto che noi osserviamo il cielo da un sistema fisico, la Terra, che, oltre a ruotare su stesso dando origine al moto diurno, si muove rispetto al Sole, che a sua volta si muove all’interno della Via Lattea, la quale si muove rispetto alle altre galassie. Inoltre le nostre osservazioni sono ancora in gran parte fatte al di sotto dell’atmosfera che rifrange e diffonde la radiazione proveniente dai corpi esterni e quindi perturba la direzione di arrivo dei segnali. I più importanti effetti dovuti alla dinamica del moto della Terra sono la precessione e la nutazione; il moto del Sole intorno alla Via Lattea e della Via Lattea attraverso il sistema delle galassie, pur essendo molto veloci, determinano variazioni solo su tempi molto lunghi, dell’ordine delle decine di milioni di anni e possono essere in prima approssimazione trascurati. Effetti legati alla fisica locale sono invece la parallasse e l’aberrazione e la rifrazione atmosferica. Si pone il problema di specificare a quale istante una coordinata si riferisce. È stato perciò inventato il concetto di epoca: tutte le coordinate si specificano rispetto ad un'epoca, ed esistono algoritmi per passare da un'epoca all'altra. 1.5.1 Precessione I corpi del sistema solare sono concentrati sul piano dell’eclittica ed esercitano una forza di attrazione gravitazionale differenziale sul rigonfiamento equatoriale della Terra che è inclinato rispetto al piano. Ne nasce un momento torsionale, dovuto principalmente al Sole e alla Luna, che dà origine ad una precessione dell’asse di rotazione terrestre e del suo piano equatoriale. Pertanto la precessione comporta una variazione della posizione del punto γ, intersezione tra equatore celeste ed eclittica; in Coordinate astronomiche – Ilaria De Angelis 8 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 particolare l’equinozio di primavera anticipa di 50 arcosecondi ogni anno, corrispondente ad un intero giro sull’eclittica con periodo di circa 26.000 anni. Se avete provato a far ruotare una trottola, saprete che il suo asse di rotazione tende a restare allineato lungo la stessa direzione, in genere verticalmente, ma anche in qualsiasi altra direzione nello spazio. Se però date un colpetto alla trottola, il suo asse comincerà ad oscillare attorno alla verticale, e il suo moto descriverà un cono (ved. disegno). Il movimento di rotazione della Terra avviene in modo simile, anche se, con una scala temporale molto più lenta, ogni rotazione dura un anno, e ogni giro attorno al cono si completa in circa 26000 anni. L'asse del cono è perpendicolare al piano dell'eclittica. La causa del movimento di precessione sta nel rigonfiamento equatoriale della Terra, dovuto alla forza centrifuga associata alla rotazione terrestre. La rotazione modifica la forma della Terra da una sfera perfetta a un globo leggermente schiacciato ai poli, che quindi è più gonfio all'equatore. L'attrazione da parte della Luna e del Sole su questo rigonfiamento è quindi il "colpetto" che produce il movimento di precessione terrestre. In un ciclo che dura 25750 anni (anno platonico), la direzione verso cui punta l'asse di rotazione terrestre in cielo si sposta lungo una grande circonferenza con un raggio di circa 23,5 gradi. La stella polare, verso cui punta l'asse terrestre (entro circa un grado) adesso, una volta era molto distante dal polo celeste, e lo sarà di nuovo fra qualche migliaio di anni (a titolo di informazione, la stella polare raggiungerà il suo massimo avvicinamento al polo celeste nel 2017). Infatti, la "stella polare" usata dagli antichi naviganti greci era diversa da quella attuale, e non era così vicina al polo celeste. Poiché le coordinate equatoriali, usate nei cataloghi, dipendono dalla definizione del Punto γ, esse variano nel tempo. I valori attuali di α e δ devono quindi essere calcolati in base alla quantità di tempo trascorso dall'epoca di riferimento. L’ascensione retta e la declinazione variano secondo le seguenti formule: Δα = [m + n sin α tan δ ] N e Δδ =[n cos α] N, dove N è il numero di anni tra il tempo cercato e l’epoca di riferimento (sia positivo che negativo). Se l’epoca di riferimento è il 1 gennaio 1950, allora m = 3.07327 secondi yr-­‐1 e n = 20,0426” yr-­‐1. Normalmente tutti i software planetari tengono conto degli effetti della precessione e calcolano i valori corretti di RA e Dec per il momento dell’osservazione. 1.5.2 Nutazione L’orbita lunare è inclinata rispetto all’eclittica, per cui il suo piano orbitale compie una precessione, che risulta avere un periodo di 18.6 anni. Questo effetto comporta una perturbazione della precessione terrestre con lo stesso periodo, detta nutazione. L’effetto è ancora quello di cambiare la longitudine e anche l’obliquità dell’eclittica: si calcola che le variazioni sono molto più piccole di quelle dovute alla precessione. In genere questo effetto può essere trascurato nei cataloghi. In figura si mostra schematicamente l’effetto complessivo della precessione e della nutazione sul moto dell’asse terrestre. Coordinate astronomiche – Ilaria De Angelis 9 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 Figura 2 Precessione e nutazione dell'asse di rotazione terrestre 1.5.3 Effetti di parallasse Osservando un oggetto vicino da posizioni differenti, lo vedremo proiettato sullo sfondo in direzioni differenti. La differenza angolare tra queste direzioni prende il nome di parallasse. In astronomia la direzione in cui sono visti gli astri vicini sullo sfondo delle stelle lontane (le stelle cosiddette fisse) è differente per diverse posizioni sulla Terra (Figura 3): per due osservatori agli antipodi sull’equatore, separati quindi dal diametro terrestre, la parallasse della Luna è di ben 57’, quella del Sole di 8.79". I cataloghi riportano le coordinate come sarebbero misurate dal centro della Terra, coordinate geocentriche, per cui occorre in alcuni casi tener conto di correzioni a seconda della posizione dell’osservatore sulla Terra e riportarsi quindi a coordinate topocentriche. Tuttavia questo effetto diventa trascurabile per quasi tutte le stelle in quanto le loro grandi distanze comportano errori di parallasse inferiori al millesimo di secondo d’arco. Poiché l’errore di parallasse diminuisce all’allontanarsi dell’oggetto, la parallasse può essere usata per valutarne la distanza: è quanto ci permettono di fare i nostri occhi nella visione stereoscopica. Per avere una parallasse cospicua anche per oggetti relativamente lontani occorre compiere osservazioni da punti molto distanti, aumentando cioè la linea di base: è quanto non possiamo fare con i nostri occhi che danno appunto una visione stereoscopica solo a distanze relativamente piccole perché la linea di base è solo di 7 cm circa. Per l’astronomia le Figura 3 linee di base sono le dimensioni della Terra e dell’orbita intorno al Sole: si parla di parallasse diurna nel primo caso e di parallasse annua nel secondo. Come vedremo più avanti, le parallassi diurne permettono di misurare le distanze all’interno del sistema solare, le parallassi annue le distanze di alcune stelle relativamente vicine. Coordinate astronomiche – Ilaria De Angelis 10 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 1.6 Misure di tempo Abbiamo già definito il tempo siderale e corrispondentemente il giorno siderale cioè l’intervallo di tempo tra due passaggi successivi del Punto γ al meridiano. Nell’uso quotidiano è invece necessario fare riferimento al moto del Sole, definendo come tempo solare la posizione del Sole rispetto al meridiano locale. Come abbiamo visto, il moto di rivoluzione della Terra intorno al Sole ha come conseguenza un moto apparente annuale del Sole attraverso le costellazioni, per cui tempo siderale e tempo solare non coincidono; in un anno il Sole perde un intero giorno per cui il giorno solare medio, inteso come tempo medio tra due successivi passaggi del Sole al meridiano, risulta essere di circa 3 minuti e 56 secondi più lungo del giorno siderale. Inoltre poiché il moto apparente del Sole lungo l’eclittica non è uniforme durante l’anno (a causa dell’orbita ellittica terrestre) e poiché l’eclittica è inclinata sull’equatore, il tempo solare vero non scorre uniformemente. La non circolarità dell’orbita terrestre comporta che il giorno solare effettivo sia differente da quello medio di una quantità variabile durante l’anno che può arrivare fino a circa 16 minuti di differenza; tale differenza va sotto il nome di equazione del tempo (vedi Fig. 4). Infine su tempi lunghi hanno influenza sulla durata dei giorni sia siderale sia solare le irregolarità della rotazione terrestre, la precessione e la nutazione. Figura 4 Equazione del tempo. La durata del giorno solare varia nel corso dell’anno visto che la velocità orbitale della Terra è diversa da un punto all’altro dell’orbita (2° legge di Keplero). La definizione del tempo solare medio è strettamente locale e quindi presenta difficoltà pratiche: città a poche miglia di distanza nella direzione est – ovest hanno culminazioni del Sole che differiscono di alcuni minuti. Per tale ragione si usa un tempo convenzionale eguale per fasce orarie o fusi orari: si tratta di 24 regioni (per ognuna delle 24 ore in cui è diviso il giorno) estese in latitudine di 360°/24 = 15° in cui si assume come ora convenzionale quella corrispondente al meridiano centrale. Il tempo del fuso orario della latitudine 0°, che corrispondente allo storico osservatorio di Greenwich, è detto Greenwich Mean Time (GMT) e viene utilizzato come riferimento. In astronomia si usa come riferimento il Tempo Universale Coordinato, conosciuto anche come tempo civile e abbreviato con l'acronimo UTC. L’UTC è derivato (e coincide a meno di approssimazioni infinitesimali) dal tempo medio di Greenwich (controllato da orologi atomici che permettono di introdurre le dovute correzioni per tener conto delle irregolarità della rotazione terrestre). Coordinate astronomiche – Ilaria De Angelis 11 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 Si ricordano inoltre le seguenti definizioni di anno: • anno siderale: è l’intervallo di tempo in cui il Sole riprende la stessa posizione rispetto alle stelle fisse, cioè la Terra compie un’orbita intera intorno al Sole; l’anno siderale corrisponde a 365.256 giorni solari medi, o analogamente a 366.256 giorni siderali. Il tempo siderale risulta di uso assai pratico in astronomia, in quanto fornisce direttamente l’ascensione retta degli astri che transitano al meridiano e permette di prevedere quali oggetti e fenomeni celesti sono osservabili da una determinata località della Terra, ma è poco adatto per gli usi civili. • anno tropico: è l’intervallo di tempo compreso tra due passaggi successivi del Sole per l’equinozio di primavera, circa 20 minuti più breve dell’anno siderale. Un anno tropico corrisponde a 365.242 giorni solari medi. La minore durata rispetto all’anno siderale è dovuta alla precessione degli equinozi, per cui l’equinozio di primavera ogni anno anticipa di 20 minuti. Questo anticipo dell’equinozio di primavera equivale nel cielo ad uno spostamento del punto di Ariete di quasi 1’ d’arco (infatti la Terra impiega una ventina di minuti a percorrere 1’ d’arco). • anno civile medio: tiene conto di 365 giorni solari e anni bisestili di 366 giorni ogni 4 anni salvo anni di inizio secolo non divisibili per 400 (365+1/4-­‐3/400= 365.2425); comporta un errore di 1 giorno ogni 3000 anni. Poiché ai fini pratici interessa soprattutto il ritorno stagionale, più che la posizione reale della Terra sull’orbita, nell’elaborare il calendario civile ci si basa sull’«anno tropico». La differenza di 20 minuti fra i due anni (siderale – tropico) potrebbe sembrare irrilevante ma in realtà con il passare dei secoli avrebbe creato non pochi problemi: ci sarebbe uno scollamento tra le stagioni in calendario ed il tempo reale di stagione. Oggi l’equinozio di primavera cadrebbe il 20 febbraio anziché il 21 marzo. È inoltre opportuno avere un numero sempre intero di giorni: 365 senza le frazioni di 5 ore 48 minuti 45 secondi 98 centesimi (come per l’anno tropico). Per correggere lo sfasamento di quasi 6 ore fu deciso ai tempi di Cesare (46 a.C.) di aggiungere un giorno ogni 4 anni ( 6 ore x 4 volte = 24 ore). Questo aggiustamento sarebbe perfetto se la differenza fra anno tropico e siderale fosse di 6 ore esatte. Però ogni anno alle 6 ore calcolate mancavano 11 minuti 14 secondi 2 centesimi che equivalgono a 8 giorni ogni mille anni. Inoltre lo spostamento dell’equinozio determina anche uno sfasamento pratico nelle stagioni, in particolare l’equinozio di primavera non cadeva più il 21 marzo. All’inizio del VIII secolo un monaco inglese fece notare che l’equinozio di primavera fissato dal Concilio di Nicea nel 325 d.C. il 21 marzo cadeva ormai il 18 marzo. Verso al fine del XVI secolo quegli 11 minuti accumulati negli anni avevano portato ad un anticipo di ben 10 giorni e l’equinozio ormai cadeva l’ 11 marzo. Nel 1582 il papa Gregorio XIII, al fine di eliminare l’anomalia deliberò che, per perdere i 10 giorni di troppo accumulati dall’epoca del Concilio di Nicea, si saltasse dal giovedì 4 ottobre al venerdì 15 ottobre. Fu contemporaneamente fissato l’anno bisestile: ogni 4 anni l’anno avrà 366 giorni. Di tutti gli anni tecnicamente bisestili non lo saranno quelli divisibili per 100 (esempio 1900, 2100, 2200) ad eccezione di quelli divisibili per 400 (esempio 2000, 2400, 2800). Il calendario che usiamo oggi è appunto il calendario gregoriano. In astronomia, oltre che l’UTC, si usa molto la data giuliana (Julian Date, JD) che conta i giorni con un numero progressivo, senza distinzione di anno o di mese, a partire dal mezzogiorno del gennaio del 4713 avanti Cristo; fu introdotta nel 1583 all’epoca della riforma del calendario gregoriano con riferimento a una data precedente a qualunque evento storico documentabile. Viene espressa con una parte intera che rappresenta i giorni trascorsi dalla data zero e una parte decimale che indica la frazione di giorno a partire dal mezzogiorno misurata in UTC. La frazione è Coordinate astronomiche – Ilaria De Angelis 12 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 trovata dividendo il tempo, espresso in ore, per 24 (ponendo 00:00 uguale a mezzogiorno, e 12:00 mezzanotte): la mezzanotte corrisponde quindi a 0.5. Il punto iniziale a mezzogiorno fa cadere un'intera notte di osservazioni in un solo giorno giuliano, invece che in due. Il sistema dei giorni giuliani è stato progettato per avere un singolo sistema di date che potesse essere usato per lavorare con differenti calendari, e per unificare differenti cronologie storiche, visto che non presenta difficoltà come anni bisestili o cambi di calendario. 1.7 Cataloghi fondamentali La costruzione di un catalogo fondamentale è una operazione molto complessa. Molti cataloghi stellari hanno infatti solo natura differenziale, cioè danno posizioni relative a un insieme di stelle fondamentali. Dal 1964 è in uso il catalogo detto FK4, contenente circa 1500 stelle brillanti. Nel 1988 è stato pubblicato il catalogo FK5, cioè la revisione del catalogo precedente, con una nuova determinazione della posizione del punto γ, con l'adozione delle nuove costanti di precessione raccomandate dall'Unione Astronomica Internazionale (IAU) nel 1976 e con l'eliminazione della aberrazione ellittica dalle coordinate medie. FK5 fornisce le posizioni e i moti propri di 1535 stelle brillanti. Fu pubblicata anche una estensione del FK5 contenente altre 3117 stelle secondarie più deboli, fino alla mag. 9.5. In occasione della 23a Assemblea Generale nel mese di agosto 1997, L’IAU ha deciso che, a decorrere dal 1 ° gennaio 1998, il sistema di riferimento fondamentale IAU è l'International Celestial Reference Frame (ICRF). L’ICRF è basato sulle posizioni (in coordinate equatoriali) di un insieme di sorgenti radio compatte extragalattiche osservate dal Very Long Baseline Interferometry (VLBI) (quindi non sulla posizione di stelle osservate nel visibile!). Il catalogo basato su questo riferimento, la cui origine è stata traslata nel baricentro del Sistema Solare, è chiamato International Celestial Reference System (ICRS) e ha sostituito il catalogo FK5 a partire dal 1988. Per maggiori dettagli vedi: http://www.usno.navy.mil/USNO/astronomical-­‐applications/astronomical-­‐information-­‐center/icrs-­‐
narrative Coordinate astronomiche – Ilaria De Angelis 13 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 Sommario di alcune definizioni temporali
Tempo Solare:
GMT: Greenwich Mean Time – Tempo Solare Medio riferito al meridiano di Greenwich
UT1: Universal Time – Tempo Solare Medio riferito a sorgenti astronomiche. Leggermente diverso
dal GMT
In questi due tempi il secondo viene definito in base alla lunghezza dell’anno che viene a sua volta
definita con approssimazione diversa in funzione dei sistemi.
UTC: Tempo Universale Coordinato – Basato sul tempo scandito da orologi atomici. Il secondo
viene definito in termini di frequenza di opportune transizioni atomiche (e della velocità della luce)
quindi in termini di costanti fisiche fondamentali.
LMT: Tempo Solare Medio Locale – si calcola in base al GMT e alla longitudine del luogo
LAT: Tempo Solare Apparente Locale – Si calcola in base al LMT tenendo conto dell’Equazione
del tempo.
CET: Central European Time – Tempo civile dell’Europa Centrale. In Italia si usa il CET. CET =
UTC + 1
Tempo Siderale:
GMST: Greenwich Mean Sideral Time – Si calcola a partire dal passaggio del punto gamma al
meridiano di Greenwich
GAST: Greenwich Apparent Sideral Time – Si ottiene dal GMST apportando la correzione per
l’effetto della nutazione terrestre.
LAST: Local Apparent Sideral Time
LMST: Local Mean Sideral Time
Si calcolano a partire dei rispettivi tempi di Greenwich tenendo conto della longitudine del luogo.
Se, approssimando, s’ignora la distinzione, si può parlare di Tempo Siderale (Locale o di
Greenwich) tout-court.
Coordinate astronomiche – Ilaria De Angelis 14 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 Calcolo della Data Giuliana (JD)
Se abbiamo una data del calendario Gregoriano come la convertiamo in Data
Giuliana (JD)?
Per prima cosa troviamo la JD corrispondente al mezzogiorno di quella data. Avremo
quindi un numero JDN che termina con .0, in quanto il giorno giuliano inizia a
mezzogiorno. Poi calcoleremo la frazione decimale.
Per calcolare il JDN a mezzogiorno si utilizza il seguente algoritmo (i residui
decimali delle divisioni vanno cancellati):
a = (14 – mese)/12
y = anno + 4800 – a
m = mese + 12a – 3
JDN = giorno + (153m + 2)/5 +365y + y/4 – y/100 + y/400 – 32045
Per il calcolo della frazione, conoscendo l’ora del giorno in ore, minuti, secondi, si
usa il seguente algoritmo (questa parte è interamente decimale):
Frac = (Ore – 12)/24 + minuti/1440 + secondi/864000
(in 24 ore ci sono 1440 minuti o 86400 secondi)
Infine:
JD = JDN + Frac
Il JD va calcolata per l’ora relativa al meridiano di Greenwich (UTC, Tempo
Coordinato Universale). Pertanto, per l’Italia, bisogna tenere conto delle differenze di
fuso orario: Il Italia usiamo il CET (Central European Time) che è +1 rispetto
all’UTC, +2 quando c’è l’ora legale.
Per un test, la JD corrispondente alle ore 12 dell’ 1/1/2000 è 2451545.0.
Uno dei siti per il calcolo diretto in rete:
http://aa.usno.navy.mil/data/docs/JulianDate.php
Coordinate astronomiche – Ilaria De Angelis 15 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 Calcolo del tempo siderale locale (LST)
Il LST di un luogo corrisponde all’ascensione retta (di un oggetto) che in quel
momento transita al meridiano locale.
Il calcolo è un po’ più complesso e richiede il calcolo preliminare della Data
Giuliana. Fissato il giorno l’ora (UTC) di Greenwich per cui si vuole effettuare il
calcolo.
Calcolare la JD usando la procedure precedente.
Calcolare:
D = JD - 2451545.0
(2451545.0 è il JD dell’1/1/2000 h12)
Calcolare il Greenwich Mean Sideral Time:
GMST = 18.697374558 + 24.06570982441908*D
GMST va riportato all’intervallo 0-24h. Quindi:
GMST = GMST/24
Di questa quantità va presa solo la parte frazionaria (per riportarsi all’intervallo tra 0
e 24 h).
Convertire la parte frazionaria di giorno in ore, minuti, secondi (es: 0.5 : 12h 00m
00s).
A questo punto abbiamo il tempo siderale del meridiano di Greenwich.
Per riportarlo al meridiano locale è necessario conoscere la longitudine del luogo.
Convertire la longitudine da gradi, primi e secondi d’arco in ore, minuti, secondi.
Chiamiamo ΔL questa quantità. (Ricordare che 15° = 1h)
Infine:
LST = GMST + ΔL (se siamo a Est di Greenwich, come è il caso dell’Italia),
altrimenti – ΔL.
La longitudine di Roma è circa: 12° 29’.
In questo calcolo si ignora la correzione dovuta alla nutazione, non rilevante per una
Coordinate astronomiche – Ilaria De Angelis 16 Laboratorio di Astrofisica -­‐ a.a. 2010-­‐11 precisione di qualche secondo.
Per ulteriori spiegazioni sul metodo di calcolo e un algoritmo di calcolo più accurato:
http://www.usno.navy.mil/USNO/astronomical-applications/astronomicalinformation-center/approx-sider-time
Uno dei siti per il calcolo diretto in rete:
http://www.csgnetwork.com/siderealjuliantimecalc.html
Coordinate astronomiche – Ilaria De Angelis