Lezioni di Astronomia
1 -Astronomia di posizione
Liceo Scientifico Copernico
Bologna 16 marzo 2010
1
I sistemi di coordinate
Servono per indicare la posizione degli oggetti
celesti
che però non è fissa
Il sole e le stelle appaiono ruotare attorno a noi
Questo moto apparente riflette il moto di
rotazione della terra attorno al proprio asse
2
3
Gemini South (1h40m) sept. 2006
4
Vienna , Jul. 2005
5
Joshua Tree National Park (Ca), 2007
6
Montlaux (France) sept. 2007 (477 exp. 30 sec each)
7
8
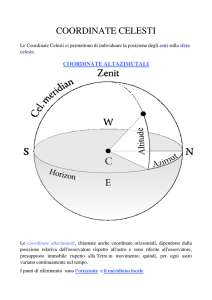
Il sistema di coordinate più intuitivo
Orizzontale (o alt-azimutale)
Zenit (o Zenith) dall’arabo
samt al-ra's o samt al-ru'ūs
(direzione della testa o
delle teste)
Nadir dall arabo nazìr al-sam
(corrispondente dello zenith)
Le coordinate sono : l’altezza (h) e l’ Azimut (A dall'arabo assumut).
9
L’altezza (h) è l’angolo fra l’astro e il
piano dell’orizzonte
E’ complementare a z (distanza
zenitale)
h= 90°- z
L’Azimut è l'angolo (sul piano dell’orizzonte) fra il SUD e il
punto dell'orizzonte in cui il cerchio massimo verticale
passante per l'astro lo incontra.
h e A si misurano in gradi
h [90 0 90 0 ]
Per essere visibili gli astri devono avere
A [00 360 0 ]
h 00
10
Le coordinate alt-azimutali :
-cambiano continuamente al variare
del tempo (gli astri appaiono muoversi
lungo la volta celeste)
- dipendono dal luogo di osservazione
SI PUO’ DEFINIRE UN SISTEMA DI COORDINATE
UNIVERSALI (INDIPENDENTI DAL TEMPO E DAL
LUOGO DI OSSERVAZIONE) ?
11
Si’, se si considera come piano di riferimento
non più l’orizzonte ma l’equatore celeste (ossia il
prolungamento dell’equatore terrestre)
La distanza angolare di un astro dall’equatore
celeste rimane costante e di conseguenza
rimane costante la distanza angolare della
proiezione del punto ove si trova l’astro (sul
Piano dell’equatore celeste) da un punto
assegnato sull’equatore celeste.
12
Il sistema di coordinate equatoriali
o R.A.
o dec.
Right Ascension , Ascensione Retta
Declination , declinazione
13
2.2 m ESO-MPI
14
15
Mount Wilson,
Hooker telescope
100 inches, 1919
16
Telescopio Hale, Monte Palomar
Il più grande al mondo (1948-1993)
17
Gran Telescopio Canarias 11 m
18
19
L’ Ascensione Retta si misura in ore minuti e secondi
La declinazione si misura in gradi e frazioni di gradi
[-90 90 ]
[0 24 ]
h
0
h
0
E’ possibile trasformare le ore in gradi, considerando che 24 h
corrispondono a 360° ed utilizzando una semplice proporzione
1 : x 24 : 360
h
0
h
0
360 1
1 x
15
24
0
h
h
0
h
20
Esercizio: determinare l’ascensione retta (in gradi) di
M 104 (el Sombrero)
R.A. : 12h 39m 59.4s
Dec : -11° 37’ 23”
R.A. : 189.9975°
21
L’altezza della stella polare è pari alla
latitudine del luogo di osservazione
22
E’ possibile passare da coordinate equatoriali a
coordinate orizzontali (e viceversa) , utilizzando la
trigonometria sferica.
Le coordinate equatoriali definiscono la pasizione di un astro in
modo definitivo….. a patto che l’astro non sia dotato di
movimento proprio.
Le coordinate equatoriali della luna dei pianeti (degli asteroidi
delle comete) cambiano.
Il moto di rivoluzione della terra attorno al sole genera
l’impressione che il sole si alzi e si abbassi
sull’orizzonte durante l’anno.
23
Coordinate equatoriali della luna , 2010, 03h
data
R.A (h:m:s)
Dec (°:’:’’)
1 gennaio
07:05:57
23:0 6:59
1 febbraio
23:06:59
04:44:28
1 marzo
11: 03:46
01:18:37
1 aprile
14:17:58
-18:45:59
1 maggio
16:46:57
-24:58:54
1 giugno
20: 02:51
-18:56:17
1 luglio
22:06: 03
-07:26:47
1 agosto
00:47:33
10:46:32
1 settembre
03:54:18
23:34:13
1 ottobre
06:32:07
23:12:23
1 novembre
10:0 0:20
07:44:14
1 dicembre
12:23:46
-08:14:0 6
(T.U.)
24
Il cambiamento delle coordinate riflette sia il movimento
della luna sia quello della terra
Anche le coordinate equatoriali del sole cambiano durante
l’anno
Non è il sole che si muove
ma la terra che orbita attorno
Ad esso lungo un piano (eclittica)
che non coincide con il piano
dell’equatore celeste.
25
26
27
28
29
30
31
32
33
34