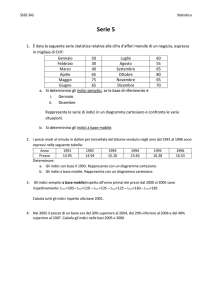
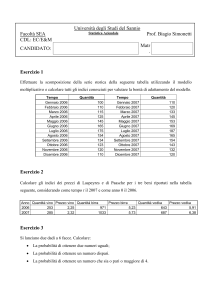
Corso di Statistica Aziendale
APPUNTI SULL’ANALISI STATISTICA DEI
BILANCI
Laura Grassini
1. Il bilancio e gli indici di bilancio
Introduzione
1.1 Lo stato patrimoniale
1.2 Il conto economico
1.3 Indici di bilancio
1.4 Schemi per l’interpretazione degli indici di bilancio
1
3
7
11
16
2. L’analisi statistica dei dati di bilancio. Introduzione e analisi
univariata
Introduzione
2.1 Comparazioni di bilancio e analisi statistica
2.2 Analisi univariata: i valori medi
2.3 Caratteristiche delle distribuzioni empiriche dei ratio
19
19
21
26
3 Analisi statistica multivariata dei dati di bilancio. Applicazione delle
componenti principali per un’analisi della concorrenza
3.1 Presupposti teorici
29
3.2 L’analisi statistica: aspetti generali
30
3.3 Analisi preliminare dei dati
33
3.4 L’analisi in componenti principali (ACP)
34
I
4. Analisi statistica multivariata dei dati di bilancio. Modelli statistici per
la previsione delle insolvenze. Un caso di studio
Introduzione
41
4.1 Premesse teoriche generali: insolvenza e cause di insolvenza
43
4.2 Analisi statistica dei bilanci e insolvenza: una breve rassegna
45
4.3 L’analisi discriminante per lo studio dell’insolvenza
50
4.4 Un caso di studio
57
5. Nota metodologica. Analisi delle componenti principali (ACP)
Introduzione
5.1 Aspetti algebrici coinvolti nell’ACP
5.2 L’ACP
5.3 La scelta del numero di componenti
5.4 Interpretazione delle componenti selezionate
5.5 ACP: matrice S o matrice R ?
5.6 Esempi numerici
65
65
66
69
70
71
73
6. Nota metodologica. Analisi discriminante (AD)
Introduzione
6.1 Analisi discriminante e problemi classificatori
6.1.1 Teoria decisionale
6.1.2 La funzione discriminante
6.1.3 Funzione discriminante e AD normale
6.1.4 Funzione discriminante e AD logistica
6.2 Stima della funzione discriminante (AD normale)
6.3 Verifica della capacità classificatoria della funzione discriminante
6.4 Esempio numerico
79
80
80
82
84
86
87
89
91
Bibliografia
95
Siti Internet di interesse
97
II
Indici di bilancio
1.
1
Il bilancio e gli indici di bilancio
Introduzione
1.1 Lo stato patrimoniale
1.2 Il conto economico
1.3 Indici di bilancio
1.4 Schemi per l’interpretazione degli indici di bilancio
Introduzione
L'analisi di bilancio è quel complesso di elaborazioni svolte sul
bilancio per interpretarne i dati, allo scopo di valutare la situazione
(economica, finanziaria, reddituale) in cui un'azienda si trova e per
prendere decisioni sulle gestioni e strategie future. Infatti, l'analisi di
bilancio è sia strumento di analisi consuntiva (e quindi opera sui
bilanci di fine esercizio) sia strumento di analisi prospettica quando
opera sui budget alternativi che un'azienda può prefigurare.
L'analisi di bilancio presuppone la possibilità di operare comparazioni
nel tempo (per studiare la dinamica aziendale), nello spazio (analisi di
settore, della concorrenza, etc.).
E’ importante sottolineare che le analisi e le comparazioni di bilancio
hanno un diverso grado di estensione e di profondità in relazione agli
obiettivi dei soggetti per i quali si compie l’analisi, e all’accessibilità
ai dati interni contabili ed extracontabili.
Oggetto dell'analisi di bilancio sono:
- lo stato patrimoniale, che registra la consistenza delle fonti e
degli impieghi del patrimonio aziendale alla fine di ogni periodo
contabile (gli stock al 31/12 di ogni anno), e che informa sulla
capacità dell'azienda a fronteggiare gli impegni finanziari;
- il conto economico che riporta i flussi di ricavo e di costo
dell'esercizio (periodo annuale) e che informa sulla capacità
dell'azienda a produrre reddito, sull’economicità dell’attività
produttiva, ecc.
2
-
Indici di bilancio
la nota integrativa che informa su aspetti quali: i criteri di
valutazione di alcune poste contabili, e che ha lo scopo di rendere
più trasparente il bilancio.
L'analisi di bilancio richiede i seguenti presupposti: (1) presupposti
oggettivi connessi alla qualità dei dati di bilancio (trasparenza) e (2)
presupposti soggettivi relativi alla preparazione e posizione
dell'analista.
Sul punto (1) dobbiamo dire che molti miglioramenti sono stati
ottenuti attraverso il recepimento della IV e della VII Direttiva CEE
mediante il d.l. n. 127 del 9/4/91 (che ha determinato la modifica
degli articoli 2424 e 2425 del Codice Civile). Tuttavia, per condurre
una significativa analisi è necessario operare degli aggiustamenti
(detti riclassificazioni) nelle poste di bilancio per ricondurci ai
principali schemi interpretativi suggeriti dagli studiosi di economia
aziendale.
Sul punto (2) si tende a distinguere fra analisi interna (ovvero
effettuata dall'azienda sulla propria gestione) e esterna (ovvero
effettuata da un organismo esterno all'azienda). Chiaramente si
configurano situazioni informative molto diverse che, nel caso di
analisi esterna, dipendono fortemente dalla forza contrattuale dell'ente
esterno.
Le tecniche più usate per l'analisi di bilancio si basano sulla
determinazione di rapporti (o ratios da cui il termine anglosassone
financial ratio analysis) o differenze fra poste contabili allo scopo di
costruire indicatori significativi della situazione aziendale, nei vari
aspetti operativi, finanziari, come meglio vedremo in seguito.
I principali limiti dell'analisi di bilancio vanno ricondotti a:
1) staticità del bilancio e quindi limiti nella rappresentazione di
realtà a meno di non disporre di serie storiche di bilanci (di regola
annuali o, più raramente, infra-annuali);
2) problema della qualità del dato nel senso della rilevanza teorica
(che significato informativo ha un determinato indice?) e
dell'accuratezza (le poste di bilancio che si usano per calcolare
l’indice di bilancio sono accurate?)1;
1
Per ‘rilevanza teorica’ intendiamo la pertinenza della grandezza empirica (es. il
rapporto di bilancio) nel misurare un determinato elemento definito in via teorica
Indici di bilancio
3
3) problemi legati alla comparabilità dei bilanci nel tempo e fra più
aziende.
In questo capitolo esamineremo la struttura del bilancio prevista dalla
legge e introdurremo gli schemi interpretativi più usati (sia per lo
stato patrimoniale sia per il conto economico). La descrizione del
bilancio viene fatta con riferimento anche al problema della qualità
del dato poiché si tratta di interpretare e utilizzare i dati
amministrativi a fini informativi e cioè ai fini della costruzione
indicatori o modelli di comportamento significativi.
1.1 Lo stato patrimoniale
La struttura dello Stato Patrimoniale dettata dalle norme tende a
distinguere aree di valori secondo il grado di liquidità ovvero di
esigibilità dei crediti (sezione attivo) e di estinzione dei debiti
(sezione passivo).
Tab. 1.1.1 Stato patrimoniale (da art. 2424 Codice Civile)
ATTIVO (impieghi)
PASSIVO (fonti)
A) Crediti vs. soci
A) Patrimonio netto
I
Capitale
B) Immobilizzazioni
II-VII Riserve
I Materiali
IX Utile (perdita)
II Immateriali
B) Fondi rischi e oneri
III Finanziarie
C) Disponibilità
I Rimanenze
II Crediti
III Att. fin. non immob.
IV Disponibilità liquide
D) Ratei e risconti
TOTALE ATTIVO
C) Tratt. fine rapporto (TFR)
D) Debiti
E) Ratei e risconti
TOTALE PASSIVO
Questa struttura si ispira ad uno schema interpretativo che consente
una distinzione delle poste rispetto al grado di liquidità ovvero al
(es. la redditività). Per accuratezza intendiamo, in questo caso, la correttezza delle
poste contabili registrate sul bilancio. Accuratezza e rilevanza teorica sono
caratteristiche che definiscono la qualità del dato contabile come informazione
statistica.
4
Indici di bilancio
tempo per il compimento della rotazione da posizione non numeraria
a posizione numeraria, che determina il cosiddetto ciclo operativo.
Ciò, relativamente alla sezione attivo, è descritto nello schema
seguente da cui si deduce che per tempo breve si dovrebbe intendere
il periodo della durata del ciclo operativo (che comprende tutte le fasi:
dall’acquisizione di materiali all’esecuzione monetaria dei crediti).
Accade, tuttavia, che il ciclo operativo muti fortemente in funzione
del tipo di attività svolta dall'azienda. Si adotta, pertanto, un ciclo
convenzionale di durata uguale all'esercizio contabile.
Fig. 1.1.1 Ciclo operativo e sezione dell’attivo
IMPIEGHI
NUMERARI
(cassa)
2° realizzo
investimento
IMPIEGHI
NON NUMERARI
(fattori produttivi)
IMPIEGHI
NUMERARI
(crediti)
1° realizzo
trasformazione
IMPIEGHI
NON NUMERA
(prodotto)
In base al concetto di ciclo operativo, la struttura dell'attivo viene così
distinta in:
• attivo fisso: realizzo oltre il tempo breve;
• attivo (capitale) circolante (anche attivo corrente): che
comprende l’attivo a breve termine (le cosiddette disponibilità) e
la liquidità immediata.
La composizione dell’attivo fisso è descritta nella Tab. 1.1.2.
Brevemente, si ricorda che le immobilizzazioni tecniche riguardano la
specifica attività dell'azienda (es. locali dove si svolge la produzione)
mentre le immobilizzazioni patrimoniali riguardano attività collaterali
che non sono direttamente connesse con la produzione (es. affitto di
abitazioni civili in possesso dell’azienda);
Indici di bilancio
5
La voce fondo ammortamento contiene gli accantonamenti di fondi
che vengono accumulati negli anni per recuperare il valore delle
immobilizzazioni che, col tempo si deprezzano (es. gli impianti).
Nella vecchia normativa, il fondo ammortamento compariva nella
sezione passiva mentre attualmente esso è inserito, col segno
negativo, nell'attivo patrimoniale ed è riferito specificatamente ad
ogni cespite ammortizzabile. Il fondo ammortamento va così a
diminuire il valore delle immobilizzazioni, fornendo il cosiddetto
attivo fisso netto (immobilizzazioni nette).
Tab. 1.1.2 Composizione dell’attivo fisso
Immobilizzazioni
Immobilizzazioni
tecniche
finanziarie
partecipazioni
Materiali:
crediti medio/lungo
terreni
fabbricati
– fondi svalutazione
attrezzature
mobili ufficio
– fondo ammortamento
Immateriali:
ricerca e sviluppo
pubblicità
licenze
diritti su brevetti
– fondo ammortamento
Immobilizzazioni
patrimoniali
terreni
immobili civili
– fondo ammortamento
La Tab. 1.1.3 descrive la composizione dell'attivo circolante.
Ovviamente, la somma dell’attivo fisso e dell’attivo circolante
fornisce il totale attivo.
6
Indici di bilancio
Tab. 1.1.4 Composizione dell'attivo circolante
Magazzino
Liquidità differita
materie
crediti vs. clienti
prodotti finiti e non finiti ratei attivi
anticipi a fornitori
altri crediti a breve
risconti attivi
– anticipi a clienti
– fondi svalutazione
– fondi svalutazione
Liquidità immediata
denaro in cassa
depositi in banca (c/c, etc.)
assimilati denaro
– fondi svalutazione
Analogamente a quanto fatto per la sezione attivo, lo schema
interpretativo della sezione passivo dello stato patrimoniale si ispira al
criterio del tempo di estinzione dei debiti.
Tab. 1.1.4 Composizione del passivo (fonti)
Passivo stabile
Passivo consolidato
(mezzi propri)
(capitale di credito a medio
e lungo termine)
capitale di rischio
mutui
riserve di capitale
presiti obbligazionari
riserve di utili
fondo TFR
debiti operativi medio/lungo
Passivo corrente
(capitale di credito
a breve)
debiti vs. fornitori
ratei passivi
debiti fin. a breve
quote a breve TFR
utile da distribuire
Confrontando gli schemi interpretativi con quello che riproduce la
struttura dello Stato Patrimoniale dettata dalla normativa vigente (v.
Tab. 1.1.1), si deduce che tale struttura riesce solo in parte a rispettare
detti schemi. Infatti, nella pratica corrente, ai fini dell'analisi di
bilancio, è necessario ricorrere a correzioni delle poste, dette
riclassificazioni. Queste operazioni hanno lo scopo di garantire
essenzialmente la rilevanza teorica del dato. Le più frequenti
riclassificazioni che vengono effettuate riguardano:
1) collocazione dei ratei e risconti attivi e passivi, rispettivamente,
nelle voci di attivo circolante e passivo a breve;
2) il fatto che parte di alcune poste dell'attivo circolante sono in
realtà fisse (es. la voce magazzino può contenere scorte di prodotti
ormai invendibili oppure è previsto un limite inferiore di
stoccaggio dei materiali o delle merci). Analogamente, alcune
poste del passivo a breve sono in realtà a lungo (es. scoperto di c/c
per un periodo superiore all’anno);
Indici di bilancio
7
3) il fatto che poste dell'attivo fisso o di debito a lungo termine siano
in realtà da considerarsi voci di breve termine (es. TFR quando si
prevede che entro l’anno ci saranno uscite del personale per
raggiunta anzianità).
A conclusione di questo paragrafo, presentiamo la Tab. 1.1.5 che
riporta, in forma molto sintetica, i dati di uno stato patrimoniale. Tali
dati ci serviranno per introdurre alcuni indici di bilancio e per le
successive esemplificazioni numeriche.
Tab. 1.1.5 Stato patrimoniale (azienda XXX; valori in Euro)
ATTIVO
1998
1999
PASSIVO
1998
Cassa
Crediti a breve
Magazzino
Attivo corrente
1550
31130
76980
109660
Immobilizzaz.
-F.do ammort.
Att. fisso netto
43170
-14620
28550
Totale attivo
138210
4000
17800
47600
69400
Debiti vs. fornitori
Debiti fin. a breve
Altri a breve
Imposte dirette
Passivo corrente
1999
14320
23890
9330
10650
58190
6850
16000
6870
4160
33880
21600
21600
22800
22800
Capitale proprio
8320
Riserve capitale
10360
Utili non distribuiti 39740
Tot capitale netto
58420
94870 Totale passivo
138210
7610
1940
28640
38190
94870
37110
-11640
Debiti a lungo t.
25470 Passivo consolidato
1.2 Il conto economico
L’articolo 2425 del Codice Civile regolamenta la struttura del conto
economico (v. Tab. 1.2.1). In particolare, esso stabilisce la
classificazione dei costi per causa (per natura) e la forma cosiddetta
scalare (successivi saldi ricavi-costi relativi alle diverse gestioni)
anziché a sezioni contrapposte (costi vs. ricavi).
8
Indici di bilancio
Tab. 1.2.1 Struttura del conto economico (in forma sintetica)
A: valore della produzione (venduta)
– B: costi della produzione (ottenuta)
(A–B) Differenza fra ricavi e costi
C: proventi e oneri finanziari
D: rettifiche di valore delle attività finanziaria
E: proventi e oneri straordinari
(A–B)+C+D+E: Risultato di esercizio prima delle imposte
– Imposte d'esercizio
Utile (reddito) d'esercizio dopo la tassazione
La struttura dettata nella normativa si ispira allo schema descritto
nella Tab. 1.2.2, che distingue la gestione di esercizio nelle varie aree
che contribuiscono alla produzione del reddito da un lato e
all’insorgenza dei costi, dall’altro.
Tab. 1.2.2 La distinzione delle aree gestionali
AREA
Ricavi, costi
(proventi oneri)
Caratteristica (operativa, tipica) operativi
Finanziaria
finanziari
Extracaratteristica (atipica,
atipici
patrimoniale)
Straordinaria
eccezionali
TOTALE
SALDO
ricavi–costi
Reddito operativo
+ saldo area finanziario
+ saldo area extratipica
+ saldo area straordinaria
Reddito d'esercizio prima
delle imposte
Schematicamente abbiamo quanto di seguito descritto.
• Area operativa. Fra i ricavi troviamo: valore della produzione
venduta (fatturato), rimanenze, incremento di valore di beni
destinati alla produzione (es. immobili). Fra i costi: costi per
materie prime, costi per servizi, per il personale, materiale di
consumo, ammortamenti, svalutazioni, accantonamenti per rischi
operativi.
• Area atipica. Fra i proventi abbiamo: proventi da partecipazione,
locazioni di immobili, rivalutazioni. Fra gli oneri: costi e oneri,
svalutazioni.
• Area finanziaria. Fra i proventi: es. da c/c bancari, BOT, CCT.
Fra gli oneri: interessi passivi.
Indici di bilancio
•
9
Area straordinaria. Essa concerne eventi straordinari nel senso
di:
a) non usuali, eccezionali rispetto a situazione 'normali'
(dismissione di strumenti, beni, etc.)
b) valori relativi ad esercizi precedenti come il recupero crediti
c) valori dipendenti da una modifica dei criteri di valutazione (es.
la valutazione delle scorte).
Si tratta, nel complesso, di fatti straordinari riguardanti qualunque
area gestionale (tipica e non).
Tenendo presente lo schema suggerito dalla dottrina, la struttura
stabilita dalla normativa (v. Tab. 1.2.1) rimane in parte insoddisfacente in quanto:
1) il concetto di area straordinaria rileva di fatto, oltre agli eventi
eccezionali (nel senso appena detto), anche fatti relativi all’area
atipica/patrimoniale;
2) affinché il confronto costi/ricavi operativi dia informazioni corrette
e significative, è necessario che i costi e i ricavi si riferiscano ai
medesimi eventi (es. costi e ricavi della produzione ottenuta durante
l'esercizio, oppure costi e ricavi della produzione venduta durante
l’esercizio).
Anche per il conto economico è necessario effettuare delle
riclassificazioni secondo schemi proposti dalla letteratura. In questa
sede ci limitiamo a riportare il modello a valore aggiunto che
classifica i costi per natura e cioè in relazione al tipo di fattore
produttivo utilizzato (costo del fattore lavoro, del capitale fisso ecc.).
Una grandezza molto significativa che scaturisce da questo schema è
il valore aggiunto, che rappresenta il valore prodotto dalla gestione
caratteristica una volta dedotti i costi di materie prime e servizi.
Ritroviamo in questo schema un aggregato a noi già noto perché usato
nella contabilità economica nazionale. Anche in questo caso, infatti, il
valore aggiunto è ricavato come differenza fra la produzione ottenuta
e costi per materie ecc., ed è quella parte del valore della produzione
che serve per la copertura dei costi relativi ai fattori produttivi
(lavoro, capitale operativo, di credito, di rischio).
10
Indici di bilancio
La Tab. 1.2.6, infine, riporta una rappresentazione sintetica di un
conto economico, i cui dati verranno in seguito usati a fini
esemplificativi.
Tab. 1.2.5 Conto economico a valore aggiunto
1.1 Fatturato
1.2 (–sconti, abbuoni, resi)
1. Fatturato netto
2.1 Rimanenze finali di prodotti
2.2 (–esistenze iniziali di prodotti)
2. Altri ricavi
3. PRODOTTO DI ESERCIZIO (1+2)
4. – Consumo di materie
5. MARGINE INDUSTRIALE LORDO (3-4)
6. – Spese operative
7. VALORE AGGIUNTO (5-6)
8. – Salari, stipendi, contributi, accanton. TFR
9. MARGINE OPERATIVO LORDO (7-8)
10. – Quote ammortamento
11 REDDITO OPERATIVO (9-10)
12. SALDO AREA FINANZIARIA (proventi-oneri fin.)
13. SALDO AREA EXTRA CARATTERISTICA
14. SALDO AREA STRAORDINARIA
15. RISULTATO PRIMA DELLE IMPOSTE (11+12+13+14)
16. – Oneri tributari
17. UTILE/PERDITA DI ESERCIZIO
Tab. 1.2.6 Conto economico. Azienda XXX.
POSTE CONTABILI
Fatturato netto (fatturato–sconti, abbuoni, resi)
– Costo della produzione
– Spese commerciali e amministrative etc.
Totale costi operativi
Reddito operativo lordo
- quote ammortamento
Reddito operativo netto
– oneri finanziari
Reddito prima delle tasse
– Oneri tributari
Utile d'esercizio (reddito globale netto)
1996
214250
151580
25270
176850
37400
2980
34420
2420
32000
16100
15900
1995
150070
107800
19040
126840
23230
3000
20230
1530
18700
9000
9700
Indici di bilancio
11
1.3 Indici di bilancio
Come si è già accennato, l'analisi mediante indici di bilancio aiuta ad
interpretare i valori contabili riportati nello stato patrimoniale e nel
conto economico. E, la determinazione dei ratio risponde, fra l’altro,
all’esigenza di eliminare eventuali differenze dimensionali esistenti
fra le varie aziende, per la costruzione di misure più correttamente
comparabili. Ad esempio, riveste poco significato il confronto fra il
risultato operativo di due imprese quando queste hanno un differente
ammontare di risorse investito nell’attività.
Possiamo distinguere due tipi di approcci ai fini del calcolo degli
indici o ratio (rapporto fra poste).
(a) Approccio verticale: gli indici sono determinati a partire da dati
appartenenti alla stessa sezione del medesimo documento contabile
(conto economico, stato patrimoniale). Un esempio di questo
procedimento è la rappresentazione dello stato patrimoniale in valori
percentuali. Da questa sono ricavabili informazioni sulla struttura
delle fonti e degli impieghi dell'azienda.
Tab 1.3.1 Composizione percentuale dello stato patrimoniale. Azienda XXX
ATTIVO
1996
1995
PASSIVO
1996
1995
Cassa
Crediti a breve
Magazzino
Attivo corrente
1.4
28.4
70.2
79.3
5.8
25.6
68.6
73.1
Passivo corrente
42.1
35.7
Attivo fisso netto
20.6
26.8
Passivo consolidato
15.6
24.0
100.0
100.0
42.3
100.0
40.3
100.0
Totale attivo
Capitale netto
Totale passivo
(in grassetto: % calcolate sul totale di sezione)
Una rappresentazione analoga può essere ottenuta per il conto
economico. Di particolare interesse è, ad esempio, la composizione
percentuale delle varie componenti di costo della gestione tipica.
Gli indici così calcolati sono un esempio di rapporti di
composizione.
12
Indici di bilancio
(b) Approccio orizzontale: gli indici sono calcolati su poste
appartenenti a: (i) differenti sezioni del medesimo conto oppure (ii)
differenti documenti contabili. Un esempio del caso (i) è il confronto
fra le componenti dell'attivo e del passivo che sono omologhe rispetto
all'orizzonte temporale (attività fisse vs. passivo consolidato o
permanente, attività correnti vs. passività correnti), in base al principio
che le fonti a lungo (breve) dovrebbero finanziare impieghi a lungo
(breve). Un esempio del caso (ii) è il confronto fra grandezze flusso
(es. reddito operativo) e grandezze fondo (es. capitale investito nella
gestione operativa) che hanno contribuito all'attività dell'azienda.
Su questi aspetti si tornerà più avanti, nel corso della descrizione dei
principali ratio aziendali usati nella pratica.
Secondo il tipo di informazione fornita, generalmente si tende a
distinguere quattro categorie di indici:
1) indici di struttura finanziaria a breve (liquidità): misurano la
capacità dell'azienda a soddisfare impegni a breve ed esprimono la
struttura delle fonti a breve;
2) indici di struttura finanziaria a lungo termine: misurano il grado
di impiego di fonti finanziarie a lungo termine e la struttura delle
attività;
3) indici di redditività: misurano la capacità dell’azienda di generare
reddito;
4) indici di attività (rotazione, turnover): misurano l'intensità di
impiego delle risorse aziendali.
A questi possono essere aggiunti gli indici di bilancio che, derivanti
dall’approccio verticale, misurano la struttura del capitale e del
patrimonio aziendale (es. quota di attivo fisso, ecc.).
1.3.1 Indici di struttura finanziaria a breve
Questi indici sono principalmente focalizzati sull'analisi della struttura
del capitale circolante di un'azienda. Alcuni di essi sono presentati
nella tabella seguente.
Come si può vedere se l'attivo è maggiore del passivo il current ratio
(CR) assume valori superiori a 1. I principali problemi connessi con
l'uso di questo indice riguardano l'eventuale presenza fra le poste
Indici di bilancio
13
correnti coinvolte, di componenti che, in realtà, sono di lungo termine
(es. scorte invendibili nell'attivo corrente, e cioè comprese nella voce
‘magazzino’) e dell'assenza di componenti breve poiché sono
registrate sotto voci a lungo termine (v. l'esempio del TFR sopra).
Tab. 1.3.2 Indici di struttura finanziaria a breve. Azienda XXX.
Indice
Descrizione
1996
Current ratio (CR)
attivo corrente/passivo corrente
1.90
Quick ratio (QR)
liquidità/passivo corrente
0.56
Quoziente di tesoreria liquidità immediate/passivo corrente
0.27
1995
2.00
0.64
0.12
Il quoziente di tesoreria e il quick ratio QR non contengono la voce
‘magazzino’ e quindi risolvono, in parte, i problemi appena
richiamati.
Facciamo notare che i tre indici appena introdotti operano un
confronto di poste contabili appartenenti a sezioni opposte dello stato
patrimoniale (approccio orizzontale), ma simili rispetto alla durata.
E’ importante sottolineare che anche la composizione percentuale del
capitale circolante (approccio verticale) informa sulla struttura
finanziaria a breve. Per la nostra azienda XXX, la cassa, ad esempio, è
passata dal 5.8% del 1995 al 1.4% del 96 denotando così una
diminuzione di liquidità (segnalata del resto anche dal quoziente di
tesoreria in Tab. 1.3.2).
1.3.2 Indici di struttura a lungo termine
Questi indici informano sulla capacità dell'azienda a sostenere gli
impegni a lungo termine. Possiamo distinguere due tipi di indici a
seconda che si misuri la forza aziendale attraverso (i) le attività
(capitale, stock) o attraverso (ii) il flusso di reddito prodotto.
Tab. 1.3.3 Indici di struttura finanziaria a lungo. Azienda XXX.
Indice
Descrizione
1996
Incidenza debiti
totale debiti/totale passivo
0.58
Indice indebitamento
totale debiti/capitale netto
1.37
Copertura oneri finanziari reddito lordo*/oneri finanziari
14.00
* reddito d’esercizio al lordo di oneri finanziari e tributari
1995
0.60
1.48
13.00
14
Indici di bilancio
Il ratio di incidenza dei debiti è un indice molto generale di struttura
finanziaria in quanto il numeratore contabilizza sia i debiti a breve sia
quelli a lungo termine (il capitale di credito: passivo corrente e
passivo consolidato). Esso informa sulla quota di risorse fornita dai
finanziatori esterni.
L’indice di indebitamento viene talvolta indicato anche come rapporto
di indebitamente o, in lingua anglosassone, debt/equity ratio. Dal
punto di vista dei creditori, un valore basso costituisce un segnale
positivo in quanto evidenzia la capacità dell'azienda a sopportare gli
impegni con fondi propri (conferiti dai soci e prodotti all'interno
dell'azienda). Dal punto di vista di chi ha conferito il capitale di
rischio, un valore basso può essere visto negativamente in quanto
un'azienda forte può ottenere credito a basso costo e quindi può
sfruttare questa possibilità per aumentare le risorse. Com’è noto,
infatti, il ricorso a capitale di credito può essere una leva (detta
appunto 'leva finanziaria') per accrescere la redditività aziendale.
Per valutare la capacità aziendale a sostenere gli oneri finanziari
(indicati in seguito con OF) generati dai prestiti a lungo termine, si
può usare l’indice di copertura degli OF. Questo ratio, che impiega
due grandezze flusso, può essere visto anche come un indice di
rotazione. Alcuni analisti preferiscono usare il reddito d'esercizio al
lordo degli OF ma al netto dell’imposizione fiscale. Ai fini della
comparabilità spazio/tempo, converrebbe usare il reddito al lordo
degli oneri tributari e non comprendere l’eventuale quota straordinaria
di reddito.
1.3.3 Indici di attività (rotazione, turnover)
Questi indici misurano il grado di utilizzo delle risorse aziendali. In
genere sono definiti, mediante l’approccio orizzontale, come il
rapporto fra grandezza flusso (dal conto economico) e grandezza stock
(dallo stato patrimoniale). Il valore dello stock può essere riferito
all'istante iniziale (1 gennaio), finale (31 dicembre) oppure può essere
una media dei due valori (o di più valori infra-annuali).
Tab. 1.3.4 Indici di rotazione. Azienda XXX.
Indice
Descrizione
Turnover magazzino
fatturato/magazzino
Turnover capitale circolante
fatturato/capitale circolante
Turnover del capitale
fatturato/totale attivo
1996
2.8
1.9
1.5
1995
3.1
2.2
1.6
Indici di bilancio
15
Riguardo al turnover di magazzino, si può osservare che, trattandosi di
valori monetari, il costo del venduto può essere una figura
maggiormente comparabile col magazzino di quanto non lo sia il
fatturato. Il turnover del magazzino aiuta a interpretare l'indicazione
fornita dalla composizione del capitale circolante. Infatti, un aumento
della voce ‘magazzino’ (in %) in corrispondenza di un aumento delle
vendite (e quindi aumento o costanza del turnover), significa che
l'azienda vuole essere pronta a soddisfare la crescente domanda di
prodotti. In caso invece di diminuzione delle vendite (e quindi del
valore del turnover), segnala che si stanno accumulando scorte che
rischiano di essere invendibili oppure che, per essere alienate, possono
richiedere uno sconto sul prezzo.
Il valore 2.8 per il turnover di magazzino significa che il fatturato
riesce a recuperare circa 3 volte il valore delle scorte.
Il reciproco di un indice di rotazione dà un indice di durata. Se la
grandezza flusso è riferita all'intervallo di 1 anno si ricavano durate in
unità-anno. Ad esempio, il reciproco del turnover di magazzino per il
1996, che è circa 0.36, indica che il magazzino viene 'ricostituito' in
una porzione di 0.36 unità anno (circa 130 giorni, assumendo 360
giorni per anno).
1.3.4 Indici di redditività
Gli indici di redditività misurano la capacità dell'azienda a ricavare
reddito dall'impiego delle risorse. Poiché, come abbiamo visto,
differenti aree gestionali possono produrre reddito, la letteratura
propone indici di redditività che mettono in luce il contributo delle
diverse gestioni al reddito globale.
Dal punto di vista statistico questi ratio possono essere considerati
come ‘indici di derivazione’ e possono essere composti sia come
rapporti fra grandezze flusso, sia come rapporti fra flusso e stock.
Il ROI (return of investment), è un indice di redditività operativa o
tipica. Esso misura la capacità dell'attività tipica dell'azienda ad
attrarre capitale (proprio e di credito) ed è espressione della politica
industriale (processo produttivo, distributivo, ecc.) dell'azienda. Il
ROI è il rapporto fra reddito operativo e capitale investito nell'attività
16
Indici di bilancio
tipica. Analogo al ROI è il ROA (return on assets) che ha, però, al
denominatore il totale attivo. Esso è più semplice da calcolare.
Il ROE (return on equity) dà una misura della redditività delle varie
gestioni aziendali rispetto al capitale di rischio. Ai fini della
comparabilità spazio/tempo è preferibile usare il reddito al lordo degli
oneri tributari ed eliminare le eventuali quote straordinarie. Il valore
del ROE dovrebbe essere confrontato col rendimento di investimenti
alternativi in modo da capire se è conveniente investire nell'azienda.
In questo senso il ROE misura la capacità dell'azienda ad attrarre
capitale di rischio.
Il ROS (return of sales) misura la redditività delle vendite. A
differenza dei due indici sopra descritti, il ROS coinvolge due
grandezze flusso.
La tabella seguente riporta i valori degli indici di redditività
dell'azienda XXX. A tale proposito si precisa che il reddito operativo
è stato calcolato dal prospetto del conto economico sommando gli
oneri finanziari (che fanno parte dell'area finanziaria) al reddito prima
delle tasse (per il 1996: 320000+2420).
Tab. 1.3.5 Indici di redditività. Azienda XXX
Indice
Descrizione
ROA
reddito operativo/totale attivo
ROS
reddito operativo/fatturato
ROE
reddito d’esercizio/capitale netto
1996
0.25
0.16
0.27
1995
0.21
0.13
0.25
1.4 Schemi per l'interpretazione degli indici
La letteratura aziendalistica sottolinea la necessità di interpretare i
valori degli indici costruendo degli schemi organici, che mettano in
luce i legami che esistono fra questi. Tali schemi, basati sulle identità
contabili implicite nel bilancio, aiutano sia ad interpretare i dati
consuntivi aziendali ma anche a mettere in luce le azioni da
intraprendere per il futuro se si tratta di bilanci preventivi.
Vediamo, a titolo esemplificativo e utilizzando il ROA come indice di
redditività operativa, due schemi frequentemente usati: (a) quello che
esprime i contributi delle varie gestioni alla redditività aziendale
(relazione fra ROE, ROA e indebitamento) e (b) quello che
approfondisce lo studio della redditività operativa.
Indici di bilancio
17
Riguardo al punto (a), ovvero all’analisi della redditività aziendale
nelle sue componenti gestionali, consideriamo le due situazioni qui
sotto descritte.
1) Il capitale è investito interamente nella gestione tipica; c'è il ricorso
al capitale di credito e β è l'indice di indebitamento (β=totale
debiti/capitale netto); 0<γ<1 è il tasso di interesse sul capitale di
credito (ovviamente si tratta di un tasso medio di indebitamento); non
c'è imposizione tributaria. In questo caso si ha:
ROE≡ROA + β (ROA – γ)
Alla formula si giunge tenendo conto che:
Tot. debiti≡β x Capitale netto Î Totale attivo≡(1+β) x Capitale netto
Oneri finanziari≡ γ x Tot. debiti Î OF≡γ x β x Capitale netto
Reddito d'esercizio≡Reddito operativo – OF
2) Il capitale è investito interamente nella gestione tipica; c'è il ricorso
al capitale di credito e β è l'indice di indebitamento; 0<γ<1 è il tasso
di interesse sul capitale di credito; c'è imposizione tributaria e 0<α<1
è l'aliquota fiscale. In questo caso si ha:
ROE ≡ (ROA + β (ROA – γ)) (1–α)
La formula appena introdotta esprime il contributo di varie aree
gestionali alla redditività globale, misurata in forma sintetica dal ROE.
La situazione di redditività di un’azienda, ai fini del confronto nel
tempo o cross section, può essere in prima battuta esaminata
attraverso il ROE, per poi venire approfondita mediante la relazione
ROE-ROA. Si può, ad esempio, verificare se la redditività operativa
ha consentito quello che viene in letteratura chiamato effetto leva, e
che è espresso da [β (ROA– γ)]. Come è noto, infatti, se ROA>γ, un
valore alto di β ha un effetto positivo sul ROE.
L’analisi può ulteriormente scendere nel particolare: ad esempio
guardando alla redditività operativa (punto (b)). Infatti, anche il ROA
può essere visto come una espressione di sintesi delle varie
operazioni coinvolte nell’attività operativa. Sfruttando i legami
contabili, possiamo scrivere:
18
Indici di bilancio
ROA≡ ROS x Turnover del capitale
Brevemente vogliamo ricordare come questa espressione sia in grado
di evidenziare due diversi comportamenti delle aziende:
•
•
quella orientata prevalentemente ad un aumento del ROS: qualità
elevata, prezzi alti, bassi volumi di vendita;
quella orientata prevalentemente ad un aumento del Turnover:
concorrenza basata su prezzi bassi e qualità non eccellente (e
quindi con poche risorse dedicate a questo aspetto), ma con alti
volumi di vendita.
Sulla base delle relazioni fra ratio qui esaminate, ai nostri scopi, è
importante fare le seguenti considerazioni:
1) gli schemi di interpretazione dei dati di bilancio, proposti dalla
letteratura aziendalistica, individuano una vera e propria gerarchia
fra gli indici, in relazione alla loro capacità di sintesi. La natura di
detta sintesi trova giustificazione e pieno significato nelle identità
contabili che implicitamente scaturiscono dalla struttura del
bilancio;
2) gli schemi di interpretazione del bilancio suggeriscono la necessità
di procedere all’analisi simultanea di una molteplicità di indici.
Attraverso questo procedimento, i vari indici trovano una loro
precisa collocazione in uno schema organico che consente una
corretta lettura dei dati. Un esempio di particolare efficacia è il
seguente. Un valore relativamente alto (ma non patologico) di β
non è necessariamente un segnale di rischio se non viene
interpretato accanto ai livelli di redditività dell’azienda.
Analisi statistica dei bilanci
2.
19
L’analisi statistica dei dati di bilancio.
Introduzione e analisi univariata
Introduzione
2.1 Comparazioni di bilancio e analisi statistica
2.2 Analisi univariata: i valori medi
2.3 Caratteristiche delle distribuzioni empiriche dei ratio
Introduzione
Nei paragrafi precedenti sono stati introdotti i principali indici di
bilancio che hanno lo scopo di fornire una misura quantitativa di
fenomeni e aspetti significativi della situazione economico-finanziaria
di un’azienda. In questo capitolo cercheremo di delineare l’impiego
dei metodi statistici in relazione ad alcuni scopi che l’analisi di
bilancio si prefigge.
2.1 Comparazioni di bilancio e analisi statistica
Come abbiamo già accennato, l’analisi di bilancio può essere rivolta
verso l’esterno, per esaminare l’ambiente competitivo in cui
un’azienda opera e, in particolare, per conoscere le prestazioni dei
propri concorrenti, i loro punti di forza e di debolezza. Analisi di
bilancio di questo tipo sono condotte anche dagli istituti di credito per
valutare i clienti ai quali concedere finanziamenti e da parte di istituti
di ricerca economica nel contesto di studi di settore di più ampio
respiro.
L’analisi di bilancio riferita a più imprese (appartenenti al medesimo
settore oppure aziende simili per area geografica, dimensioni, ecc.)
può offrire utili conoscenze riguardo alla posizione relativa occupata
da una data azienda nel settore (o nell’area geografica, ecc.) o
riguardo a eventuali somiglianze o differenze fra imprese operanti in
settori diversi.
La comparazione fra indici di bilancio di una singola azienda e dati
aggregati, inoltre, può essere utile quando un’impresa deve decidere
se entrare in un nuovo settore o vuole confrontarsi con i dati medi del
settore di appartenenza per comprendere se i suoi risultati si allineano
20 Analisi statistica dei bilanci
con quelli del settore o, ancora, per analizzare le tendenze del settore
stesso.
La situazione occupata da un’azienda può essere valutata anche
confrontando gli indici di bilancio con i cosiddetti quozienti tipo o
standard. I quozienti standard sono i valori che, in una situazione
normale di settore, assumono gli indici di bilancio. Tali quozienti
standard vengono determinati mediante il calcolo di valori medi su
gruppi di imprese che evidenziano, per l’appunto, comportamenti
normali (imprese non eccessivamente in situazione critica né in
posizione di eccellenza). Ovviamente, il quoziente standard è
sottoposto a un continuo aggiornamento per il mutare delle condizioni
ambientali.
Tenendo presente le varie finalità che l’analisi di bilancio riferita a più
imprese può avere e i criteri, dettati dalle disciplina aziendali, per la
determinazione e interpretazione degli indici di bilancio, possiamo
schematicamente indicare alcuni ruoli che la statistica può rivestire in
merito.
1) Analisi statistica univariata. Con riferimento ai dati di bilancio di
un gruppo di imprese, essa consente lo studio della distribuzione
dell’indice di bilancio ed il calcolo di valori medi quali: indici di
posizione, indici di variabilità. La lettura dei valori medi (ad es. ROE,
ROI ecc. medi di settore) potrebbe essere condotta applicando gli
schemi interpretativi prima esposti, per la valutazione, quindi, dello
stato di salute del settore aggregato.
2) Analisi statistica multivariata. Abbiamo già sottolineato la
necessità di interpretare i dati di bilancio mediante una lettura
simultanea di più indici significativi. E, come abbiamo visto, sono
disponibili schemi interpretativi basati su una struttura gerarchica
degli indici di bilancio, in relazione al loro livello di sintesi. L’analisi
inizia ad un grado elevato di sintesi per poi scendere più nel
particolare. Ebbene, tali schemi appaiono rigidi e statici in quanto
basati esclusivamente sulle identità contabili, sempre (per definizione)
verificate all’interno del bilancio. I metodi statistici multivariati
possono offrire elementi di sintesi sulla base, non delle identità, bensì
sui legami di interrelazioni che sussistono fra gli indici. Queste
interrelazioni sono evidentemente influenzate anche dall’esistenza di
legami contabili, e pertanto, esprimono la coerenza interna dei dati di
bilancio. Tali metodi appaiono più flessibili, in quanto adattabili alle
Analisi statistica dei bilanci
21
specifiche finalità dell’analisi e capaci di fornire chiavi di lettura
maggiormente calate nella realtà del fenomeno indagato.
E’ importante sottolineare che la decisione per un’analisi multivariata
non esclude la necessità di effettuare uno studio univariato: anzi
questo deve essere sempre condotto anche se solo come esame
preliminare dei dati osservati.
Riguardo al modo di procedere nell’analisi statistica multivariata,
possiamo distinguere due diversi approcci, ciascuno dei quali può
rivelarsi conveniente in relazione alle particolari finalità dello studio.
A) Approccio esplorativo. Esso consiste, in senso molto generale,
nell’individuazione di strutture interne ai dati di osservazione,
strutture che possono evidenziare somiglianze fra gruppi di unità (nel
nostro caso le aziende) oppure legami di interdipendenza fra variabili
(nel nostro caso gli indici di bilancio o altre caratteristiche possedute
dalle aziende). Tale approccio consente di esaminare i dati secondo
‘prospettive’ o ‘punti di osservazione’ che facilitano lo studio
simultaneo di più variabili e più unità. In questo scritto mostreremo
l’impiego di un procedimento esplorativo multivariato (il metodo
delle componenti principali), nell’ambito di un caso di analisi della
concorrenza.
B) Approccio confermativo. Si tratta di specificare un modello
probabilistico che si ritiene possa avere generato i dati di
osservazione. Tale modello deve essere stimato e verificato
(confermato) sui dati empirici mediante il riscorso ai metodi
dell’inferenza statistica. In generale, lo scopo principale è quello di
specificare e stimare modelli che descrivono il comportamento delle
aziende. Relativamente a questo ambito di analisi, svolgeremo un caso
di studio concernente l’impiego dell’analisi discriminante per la
previsione delle insolvenze aziendali (modelli di credit scoring).
2.2 Analisi univariata: i valori medi
Nell’analisi finanziaria, il calcolo dei ratio di bilancio risponde
all’esigenza di eliminare eventuali differenze dimensionali esistenti
fra le varie aziende, per la costruzione di misure più correttamente
comparabili. Ad esempio, riveste poco significato il confronto fra il
risultato operativo di due imprese quando queste hanno un differente
ammontare di risorse investito nell’attività.
L'efficacia deflativa del ratio ha importanti implicazioni anche nella
formulazione di un corretto indice di posizione o valore medio.
22 Analisi statistica dei bilanci
Si consideri un gruppo di n aziende; per ogni unità i (i=1,…,n), è stato
calcolato l’indice di bilancio ri=Yi/Xi. (dove Xi>0). In questo caso si
pone spesso la questione se, come indice medio di posizione, sia più
corretto calcolare la media aritmetica semplice:
(1/n)Σi ri =(1/n)ΣiYi/Xi
oppure il rapporto fra i due aggregati (numeratore e denominatore)
ovvero fra le due medie o fra i due rispettivi totali:
Σi Yi /ΣiXi=)Σiri Xi/ΣiXi
che, come si vede, è la media aritmetica ponderata dei ratio, con pesi
pari a Xi.
Un possibile criterio di scelta fra questi due tipi di media ci viene
fornito ricorrendo alla modellistica statistica.
Supponiamo che gli n valori ri siano stati generati dal seguente
modello, dove r rappresenta il valore medio di riferimento:
(2.2.1)
MOD1
ri = Yi/Xi= r + ei
E(ei)=0
V(ei)=σ2 costante per ogni i.
L'applicazione del metodo dei minimi quadrati (che fornisce il
migliore stimatore lineare e corretto di r), ci dà la media aritmetica
semplice degli ri come stima di r. Infatti, la media aritmetica dei ratio
verifica l'espressione:
min r Σi (Yi/Xi–r)2
MOD1
implica (poiché V(ei) è ipotizzata costante) che, all'aumentare
della dimensione del denominatore, i valori ri tendono a esibire la
stessa dispersione intorno a r.
Se invece i valori ri sono generati dal modello:
(2.2.2)
MOD2
ri =r+ εi
E(εi)=0
V(εi)=σ2/Xi
il migliore stimatore lineare e corretto di r è fornito dal metodo dei
minimi quadrati ponderati. Tale stima è la media aritmetica ponderata
dei ri con pesi pari a Xi e cioè:
Analisi statistica dei bilanci
23
ΣiYi/ΣiXi = Σi riXi /ΣiXi .
Si ritrova una grandezza già introdotta sopra: il ratio per l’aggregato
delle unità nel suo insieme ovvero il rapporto fra la media (o il totale)
di Y e la media (o il totale) di X. Come si è detto, tale risultato si
ottiene stimando r dalla (2.2.2) mediante il metodo dei minimi
quadrati ponderati, e cioè risolvendo in r l'espressione:
min r Σi (Yi/Xi–r)2Xi
implica (poiché V(εi) è ipotizzata decrescente in Xi) che,
all'aumentare della dimensione del denominatore, i valori ri tendono
a esibire una dispersione minore intorno a r.
A titolo esemplificativo riportiamo il grafico per gli indici CR e ROS
relativo ad un gruppo di 200 aziende operanti nelle regioni dell’Italia
del nord-est. Come si può vedere dalla Fig. 2.2.1, all'aumentare delle
passività correnti (denominatore del current ratio) il valore di questo
tenda a stabilizzarsi. Pertanto sembra adeguato il modello MOD2; la
linea orizzontale è la stima di r mediante la media aritmetica
ponderata, che è pari a 1.214.
La diminuzione della variabilità dei valori del ratio all'aumentare del
denominatore non è altrettanto marcata per il ROS (Fig. 2.2.2). La
stima del valore medio è stata quindi ottenuta ipotizzando il modello
MOD1. La linea orizzontale rappresenta la media aritmetica dei ratio
ed è uguala a 0.05.
Nella pratica si tende ad utilizzare la media ponderata per il suo
significato più immediato: essa rappresenta infatti l'indice di bilancio
per l'intero aggregato delle aziende.
La validità di questi tipi di media può essere messa in discussione
dalla presenza di valori eccezionali o anomali (outlier). Un outlier è
una unità che si comporta in maniera molto diversa dalla maggioranza
delle osservazioni (es. un valore troppo elevato e distante dalla gran
massa dei valori).
MOD2
24 Analisi statistica dei bilanci
Fig. 2.2.1 Indice CR (current ratio)
3
Current ratio (ri)
2,5
2
1,5
1
0,5
0
5000
10000
15000
20000
25000
30000
35000
40000
Passivo corrente (Xi)
Fig. 2.2.2 Indice ROS
0,25
0,2
ROS
0,15
0,1
0,05
0
0
20000
40000
60000
Fatturato
80000
100000
Analisi statistica dei bilanci
25
La presenza di (numerosi) outlier nelle distribuzioni empiriche dei
ratio è stata evidenziata da vari studi. Generalmente si ritiene che le
unità anomale non debbano essere eliminate nell'analisi statistica in
quanto contribuiscono a caratterizzare la distribuzione stessa. Tuttavia
le medie come quelle viste in precedenza, tendono ad essere
influenzate, anche in modo abbastanza pesante, dalla presenza di
outliers e rischiano di perdere il significato di indice medio di
posizione. In questo caso possiamo adottare le seguenti alternative.
1) Ricorso ad altri indici di posizione più resistenti ai valori
eccezionali. Primi fra tutti: mediana e quartili (percentili, ecc.). Il
calcolo di questi indici di posizione per le distribuzioni empiriche
degli indici di bilancio è molto frequente (v. ad esempio le
pubblicazioni a cura della Centrale dei Bilanci dell’ABI;
www.centraledeibilanci.it) in quanto fornisce informazioni
riguardo alla posizione relativa occupata da una data azienda.
2) Analisi della distribuzione empirica del ratio allo scopo di
individuare i valori eccezionali. Questo procedimento, a nostro
avviso, è di particolare efficacia per descrivere la struttura delle
osservazioni. Seguendo questa impostazione, gli outlier
individuati (soprattutto se adeguatamente numerosi) potrebbero
andare a costituire gruppi di unità portatrici di peculiari
caratteristiche e rappresentare significativi elementi di riferimento.
E, nel contempo, le unità non outlier potrebbero esprimere quella
situazione di ‘normale gestione’ rispetto alla quale diventerebbe
possibile calcolare i quozienti standard.
2.3 Caratteristiche delle distribuzioni empiriche dei ratio
In questo paragrafo delineiamo, ricorrendo a vari strumenti statistici
(grafici, indici di forma) le principali caratteristiche delle distribuzioni
empiriche dei rapporti di bilancio.
Iniziamo con la rappresentazione grafica detta box-plot. Essa è in
grado di rappresentare gli indici di posizione, la variabilità della
distribuzione, e identificare eventuali valori anomali presenti.
La Fig. 2.3.1 è il box plot dei dati relativi all’indice di redditività ROI
per 400 aziende operanti nell'Italia settentrionale. Il grafico è
costituito da una scatola (box) rappresentata dal primo e terzo
quartile. All’interno della scatola è indicata la posizione della mediana
(secondo quartile). Un valore della mediana distante dal centro della
26 Analisi statistica dei bilanci
scatola è segnale di una distribuzione asimmetrica. L’altezza della
scatole esprime lo scarto interquartile; una scatola alta indica quindi
una più alta variabilità.
Indicando con H l’altezza della scatola, nella figura è stata individuata
una zona di valori non anomali, che è distante dalla scatole una
quantità H. Le linee (detti baffi o whisker) che partono dalla scatola
indicano il range dei valori che stanno all’interno di detto intervallo.
Punti distanti dalla scatola più della quantità H ma meno di 2H sono
outliers e vengono indicati da un pallino. Valori che si collocando ad
una distanza dal box superiore a 2H sono detti valori estremi e sono
indicati con un asterisco. La Fig. 2.3.2 schematizza la costruzione del
box-plot.
La Fig. 2.3.1 evidenzia la presenza di un valore eccezionale che
potrebbe essere anche causato da un errore di digitazione dei valori
sui quali è stato calcolato il ROI. E’ inoltre presente un gruppo
osservazioni anomale in corrispondenza di valori elevati di ROI.
Le distribuzioni cross section dei dati di bilancio, seppur riferite a
gruppi omogenei di aziende (es. rispetto alla dimensione, al settore di
attività, ecc.), sono caratterizzate dalla presenza di una forte
asimmetria e da elevata curtosi (oltre che dalla presenza di valori
eccezionali come appare nel box plot).
Fig. 2.3.1 Box-plot dell’indice ROI
0.4
0.3
0.2
0.1
Non-Outlier Max
Non-Outlier Min
75%
25%
0
ROI
Mediana
Analisi statistica dei bilanci
27
Fig. 2.3.2 Interpretazione del box plot
valori eccezionali (estremi)
outlier
2H
1.5 H
H
Non-Outlier Max
Non-Outlier Min
1.5 H
75%
25%
Mediana
Indicando con ri il generico indice di bilancio riferito all’unità i-esima
(i=,1…,n), gli indici di asimmetria (o skewness) e curtosi sono
generalmente calcolati secondo le formule seguenti:
n
3
∑ (ri − r )
Asimmetria = i =1
s r3
n
4
∑ (ri − r )
Curtosi = i =1
s r4
−3
dove:
n
∑ ri
r = i =1
n
sr =
(ri − r ) 2
n
Vale la pena notare che, nel caso di distribuzione normale, i due indici
assumono valore zero. Valori positivi dell’indice di asimmetria
denotano asimmetria positiva (v. distribuzione χ2). Valori positivi
(negativi) dell’indice di curtosi denotano una distribuzione
leptocurtica (platicurtica).
La tabella seguente riporta i valori degli indici di asimmetria e curtosi
per alcuni ratio di bilancio, calcolati sulle 400 osservazioni già
descritte.
28 Analisi statistica dei bilanci
Tab. 2.3.1 Indici statistici delle distribuzioni di alcuni ratio
RATIO
ROI
ROS
CR
TURN. ATT.
MEDIA
VARIANZA
0.092
0.067
1.324
1.428
ASIMMETRIA
0.006
0.003
0.420
0.479
CURTOSI
1.299
1.177
3.392
3.028
3.260
7.395
16.218
21.301
Come si può facilmente vedere, le distribuzioni hanno tutte una
asimmetria positiva e sono leptocurtiche. Qui sotto presentiamo il
normal probability plot del current ratio. Tale grafico evidenzia, in
modo molto chiaro, la non normalità della distribuzione dell'indice di
bilancio.
Fig. 2.3.3 Normal probability plot per il current ratio
3.5
Normale standard
2.5
1.5
0.5
-0.5
-1.5
-2.5
-3.5
-0.5
0.5
1.5
2.5
3.5
Current Ratio
4.5
5.5
6.5
Analisi delle concorrenza
3.
29
Analisi statistica multivariata dei dati di bilancio.
Applicazione delle componenti principali
per un’analisi della concorrenza
3.1 Presupposti teorici
3.2 L’analisi statistica: aspetti generali
3.3 Analisi preliminare dei dati
3.4 L’analisi in componenti principali (ACP)
3.1 Presupposti teorici
L’analisi della concorrenza è una delle metodologie necessarie per lo
sviluppo coerente del processo di formulazione della strategia
aziendale. Essa, se basata sulla logica della comparazione
interaziendale, dovrebbe essere condotta secondo un’impostazione
bifocale: tenendo presente le logiche competitive del settore ed il
comportamento degli attori rilevanti.
L’ipotesi concettuale sulla quale si fonda questa metodologia di
analisi è che in ogni settore sia possibile individuare dei gruppi di
imprese che esprimono strategie competitive simili e anche imprese
leader i cui risultati sono migliori del resto o della maggioranza dei
concorrenti.
Gli elementi che, secondo la letteratura e le analisi empiriche,
sembrano importanti per valutare la capacità o la forza di competere di
un’azienda sono:
• la performance economica: grado di redditività dell’azienda;
• situazione finanziaria comprendente la situazione di liquidità, il
livello di rischio derivante dalla struttura del capitale, l’andamento
nel tempo dei flussi di cassa (es. trend crescente, ciclicità,
stagionalità, ecc.);
• posizione prodotto-mercato dell’azienda: può essere sintetizzata
dalla quota di mercato o dal fatturato anche se altri indicatori più
complessi sono stati sviluppati;
• immobilizzazioni e fonti di approvvigionamento (energia,
impianti, ecc.): questo aspetto concerne i livelli di possibile
espansione dell’attività;
30
•
•
•
•
Analisi della concorrenza
risorse umane: struttura del personale anche in termini di età,
preparazione, ecc.;
programmi R&D la cui portata può essere evidenziata dalla spesa
destinata a questa funzione;
base tecnologica: questa è importante nella definizione della
potenziale espansione dell’attività aziendale;
marketing, distribuzione e produzione: livelli di efficienza,
efficacia, produttività e relativa possibilità di espansione
potenziale.
Da quanto sopra elencato, vediamo che informazioni sul
comportamento delle aziende possono essere desunte da un’analisi di
bilancio di imprese concorrenti.
Presupposto fondamentale è evidentemente la corretta definizione
dell’ambiente significativo per l’analisi e degli attori ivi operanti (i
concorrenti). Questo procedimento conduce, anche se non
esclusivamente, ad effettuare una comparazione fra aziende (cross
section), e pertanto porta a risultati significativi e di rilievo solo se
viene effettuato nei confronti dei concorrenti diretti che possiamo qui
definire come tutte le aziende che svolgono la medesima attività e si
presentano sui medesimi mercati di sbocco/acquisizione. Alla luce di
questa definizione, i concorrenti costituiscono quello che si chiama
comparto, che comprende tutte le aziende impegnate in un effettivo e
permanente confronto competitivo.
3.2 L’analisi statistica: aspetti generali
In questo ambito di applicazione, l’analisi statistica di bilanci di
aziende concorrenti, può servire a individuare la posizione che una
data azienda occupa nel comparto di interesse. Dalla evidenziazione di
eventuali posizioni differenti o simili, si dovrà successivamente
risalire ai possibili fattori causali che hanno influito, fattori che
possono aver agito anche a livello macro (es. evoluzione del settore).
Ai fini di uno studio della concorrenza basato su dati di bilancio, le
fasi di un’analisi statistica possono essere così di seguito individuate.
Fase 1
Definizione della popolazione di riferimento rispetto al comparto
produttivo, al tempo (esercizio), al luogo (es. regione geografica).
Analisi delle concorrenza
31
Nel caso qui esemplificato, che riguarda l’azienda XXX del comparto
produttivo Tessile operante nel Nord Italia, facciamo riferimento ai
dati di bilancio (anno 1994) di un gruppo di 52 aziende operanti,
anch’esse, nel Nord Italia.
Fase 2
Scelta dei caratteri statistici (variabili) da considerare nell’analisi. Con
riferimento ai punti elencati nel primo paragrafo indichiamo gli indici
di bilancio che vengono utilizzati.
• la performance economica: redditività del capitale proprio
(ROE), redditività operativa (ROI);
• situazione finanziaria: indici di liquidità (CR:current ratio, QR:
quick ratio); indici di leverage (rapporto di indebitamento);
• posizione prodotto-mercato: fatturato relativo al totale delle
unità analizzate (quota di mercato);
• programmi R&D
• base tecnologica
• marketing ecc. : per queste voci usiamo la quota di attivo rivestita
dalla posta di bilancio denominata ‘immobilizzazioni immateriali’.
Se l’informazione disponibile è limitata ai dati di bilancio, alcuni
importanti aspetti coinvolti nell’analisi della concorrenza non possono
essere esaminati. Ad esempio dai dati di bilancio non è disponibile la
struttura quali-quantitativa delle risorse umane.
La Tab. 3.2.1 riassume gli indici di bilancio appena descritti. Si può
osservare che QUOTA non è propriamente un indice di bilancio nel
senso tradizionale, in quanto è costruito mediante il rapporto fra il
fatturato della singola azienda ed il fatturato dell’aggregato totale.
Nella letteratura anglosassone questo tipo di rapporto è detto market
based ratio. QUOTA rientra, comunque, fra le misure di performance
economica come ROE e ROI.
Tab. 3.2.1 Indici (ratio) di bilancio
Indice
Definizione
Categoria
Redditività,
ROE
risultato netto/capitale netto
performance
ROI
risultato operativo/capitale investito
QUOTA quota di mercato (in %)
Struttura
CR
attività correnti/passività correnti
finanziaria a breve QR
liquidità/passività correnti
e lungo termine
MTCI
(passivo corrente+consolidato)/capitale investito
Struttura capitale RS
immobilizzazioni immateriali*/tot. attivo (in%)
* brevetti, spese in ricerca e sviluppo, marketing
32
Analisi della concorrenza
Per la struttura finanziaria a breve termine troviamo il CR, il QR e un
indice che misura il grado di ricorso al credito (MTCI).
Infine, l’indice RS è stato collocato nella categoria della struttura del
capitale investito in quanto è un rapporto di composizione della
sezione attivo dello stato patrimoniale (approccio verticale). Da
notare, infine, che QUOTA e RS sono espressi in termini percentuali.
Fase 3
Concerne la scelta dei metodi statistici di analisi nell’ottica di
individuare gruppi di imprese che si possano ritenere abbastanza
omogenee rispetto alle variabili considerate (imprese che esprimono
strategie competitive simili) o che, per la loro posizione rispetto alle
altre unità, possano essere considerate imprese leader nel comparto.
Per come viene formulata la questione, si richiede l’impiego di metodi
statistici multivariati. Infatti l’ottica aziendalistica dell’analisi di
bilancio tende a considerare simultanemente più indici di bilancio
ovvero più caratteristiche della struttura e gestione aziendale. Tale
analisi, opera attraverso schemi interpretativi basati sulle relazioni
contabili fra le poste (e, di conseguenza, fra gli indici). Se
consideriamo, ad esempio, l’analisi della redditività operativa che
scompone il ROI nel prodotto fra gli indici ROS e turnover, nella
mente dell’analista è presente una variabile di sintesi del fenomeno
(il ROI) che viene scomposta in componenti espressive di aspetti
significativi del fenomeno, sfruttando i legami esistenti fra gli indici,
legami che sono basati su identità contabili.
La caratteristica delle osservazioni (indici di bilancio: variabili
quantitative) e la natura prevalentemente esplorativa dello studio
(ovvero non esiste un modello di comportamento da verificare)
suggerisce l’impiego di un metodo di riduzione dei dati come l’analisi
delle componenti principali (ACP) che, nel caso presente, può
perseguire i seguenti scopi:
1) le componenti individuate dal metodo possono identificarsi con
significative variabili di sintesi del fenomeno. Tali variabili di
sintesi avrebbero qui un significato più ampio in quanto non
derivano da identità contabili ma dal sistema di interrelazioni fra
gli indici espresso dalla corrispondente matrice di covarianza o di
correlazione;
2) l’individuazione di gruppi di imprese con caratteristiche simili
ovvero di imprese leader può avvenire mediante un’analisi grafica
rispetto alle variabili di sintesi individuate attraverso l’ACP.
Analisi delle concorrenza
33
3.3 Analisi preliminare dei dati
L’applicazione di una metodologia statistica multivariata, come è
appunto l’ACP, richiede sempre un’analisi univariata preliminare,
volta a studiare le principali caratteristiche distributive delle singole
variabili.
La Tab. 3.3.1 mostra i valori dei principali indici sintetici: media
aritmetica, scarto quadratico medio (SQM), coefficiente di variazione
(CV, che è il rapporto fra SQM e media aritmetica), indice di
asimmetria e di curtosi (v. capitolo 2).
Tab. 3.3.1 Principali caratteristiche distributive degli indici di bilancio
Media
Minimo Massimo
SQM
CV
Asimm. Curtosi
Indici
ROE
0.067 -0.279
0.688
0.174
2.595
1.649
5.088
ROI
0.076 -0.012
0.412
0.078
1.024
2.240
5.985
CR
1.309
0.685
3.212
0.495
0.378
1.959
4.564
QR
0.884
0.169
2.256
0.409
0.463
1.597
2.896
MTCI
0.787
0.360
1.034
0.151
0.192 -0.976
0.724
QUOTA(%) 0.903
0.016
6.235
1.258
1.393
2.594
7.076
0.883
0.004
6.120
1.128
1.277
2.756
9.625
RS(%)
SQM: scarto quadratico medio; CV=coefficiente di variazione.
Dalla Tab. 3.3.1 possiamo notare che, mediamente, la redditività
globale espressa dal ROE è pari al 6.7% e quella operativa è pari al
7.6% anche se la presenza di valori negativi denota situazioni di
perdita.
La struttura finanziaria a breve è mediamente soddisfacente con un
CR di poco superiore a 1 e QR vicino a 0.9. In media, l’indebitamento
totale raggiunge circa il 79% del capitale investito nella gestione
caratteristica (v. indice MTCI). Il mercato si presenta frammentato: la
quota di media è inferiore al 1% con una punta massima del 6%.
Analogo è l’andamento della percentuale di attivo destinata a spese
per la ricerca e per attività di marketing (RS).
I valori del CV consentono di confrontare la variabilità di grandezze
con scala diversa (QUOTA e RS, a differenza degli altri indici, sono
in valori percentuali). Si nota una maggior omogeneità delle unità
rispetto alle variabili strutturali QR, CR, MTCI. La più alta variabilità
di ROE rispetto a ROI indica un’incidenza differenziata della gestione
extra-caratteristica.
Gli indici di asimmetria e di curtosi evidenziano una peculiarità delle
distribuzioni degli indici di bilancio: l’asimmetria (in prevalenza di
tipo positivo) e l’eccessiva curtosi. Tali distribuzioni non verificano,
pertanto, due proprietà tipiche della distribuzione normale. Ai fini
34
Analisi della concorrenza
dell’applicazione del metodo ACP ciò non rappresenta un problema
dal momento che non è necessario introdurre alcun modello
probabilistico (e quindi nemmeno quello normale), dato che l’ACP è
una metodologia esplorativa di analisi dei dati.
3.4 L’analisi in componenti principali
Le fasi per la conduzione e l’interpretazione di una ACP possono
essere riassunte nei punti seguenti:
1) scelta della matrice sulla quale condurre l’analisi: di covarianza o
di correlazione;
2) estrazione delle componenti e valutazione della capacità di
riduzione dei dati;
3) interpretazione delle componenti scelte;
4) analisi dei dati rispetto alle componenti individuate e, attraverso
queste, rilettura del fenomeno rispetto alle variabili originarie.
1) Scelta della matrice sulla quale condurre l’ACP. Come sappiamo, i
risultati di una ACP sulla matrice di correlazione sono, in generale,
diversi da quelli ottenuti usando la matrice di covarianza, pertanto è
necessario operare una scelta. Nel caso presente, gli indici di bilancio
non sono grandezze espresse in diversa unità di misura in quanto
trattasi di ‘numeri puri’ (rapporti fra poste di valori monetari).
Tuttavia, i 7 indici di bilancio hanno scala diversa. Infatti QUOTA e
RS sono espressi in percentuale, mentre non lo sono, ad esempio,
ROE e ROI. Differenze di scala esistono, tuttavia, anche fra ROI e
CR: lo scarto quadratico medio di CR è circa 6 volte quello di ROI.
In questo caso ci dobbiamo porre la seguente domanda: i valori dello
scarto quadratico medio (e quindi della varianza) rispecchiano
l’importanza che le variabili hanno, in riferimento al fenomeno
indagato? Se la risposta è affermativa possiamo condurre l’ACP sulla
matrice di covarianza, altrimenti conviene usare quella di
correlazione. La matrice di correlazione è la matrice di varianza e
covarianza delle variabili standardizzate, ovvero di variabili che hanno
tutte varianza unitaria (e quindi stessa importanza).
Nel caso presente optiamo per la matrice di correlazione, che è
riportata nella Tab. 3.4.1 (dal momento che è simmetrica, presentiamo
solo i valori della parte triangolare inferiore). Tale matrice esprime i
legami di associazione (correlazione lineare) fra gli indici e quindi
ingloba implicitamente l’effetto di vincoli e identità contabili insite
nei dati. Vediamo, ad esempio, una forte correlazione fra gli indici di
Analisi delle concorrenza
35
redditività e fra quelli di struttura finanziaria (v. valori in grassetto).
Da notare il segno negativo del coefficiente di correlazione lineare fra
CR e MTCI e fra QR e MTCI: all’aumentare di MTCI ovvero
all’aumentare del grado complessivo di indebitamento, si abbassano i
valori di CR e QR. Relazioni molto tenui presentano QUOTA e RS,
sia fra loro sia con gli altri ratio.
Tab. 3.4.1 Matrice di correlazione
ROE
ROI
CR
Indici
ROE
1.000
ROI
1.000
0.830
CR
-0.002
0.068
1.000
QR
0.034
0.193
0.871
MTCI
-0.181
-0.333
-0.782
QUOTA
0.086
0.117
-0.128
RS
-0.265
-0.144
-0.155
QR
MTCI
QUOTA
1.000
-0.749
-0.059
-0.094
1.000
0.002
-0.013
1.000
0.086
RS
1.000
E’ chiaro che l’ACP presuppone la validità della correlazione lineare
nel rappresentare i legami fra le variabili. Pertanto lo scatterplot
multiplo, riportato in Fig. 3.4.1, può aiutare nella lettura dei valori
della matrice di correlazione. Ogni diagramma a punti che compone il
grafico riporta, in ascissa, i valori della variabile indicata in alto; in
ordinata, i valori della variabile indicata a destra. Sulla diagonale si
trovano gli istogrammi di frequenza.
Fig. 3.4.1 Scatterplot matrix
ROE
ROA
CR
QR
MTCI
QUOTA
RS
36
Analisi della concorrenza
Come si può facilmente notare, in alcuni casi la Fig. 3.4.1 non
evidenzia chiari legami associativi di tipo lineare come, del resto, già
era emerso dalla lettura della matrice di correlazione. La presenza di
variabili poco correlate tende a limitare l’efficacia dell’ACP quale
metodo di riduzione dei dati.
2) Estrazione delle componenti. La matrice di correlazione, di
dimensione 7x7, non evidenzia situazioni di perfetta dipendenza
lineare fra variabili, pertanto si avranno 7 autovalori positivi. Questi
sono riportati in ordine decrescente, nella Tab. 3.4.2. Come è noto
ciascuno di essi esprime la varianza spettante ad una componente
principale (agli autovalori più grandi sono associate le componenti
più importanti).
Dalla Tab. 3.4.2 è importante notare che:
• la somma degli autovalori è uguale alla somma delle varianze
delle variabili originarie (attenzione: le varianze sono tutte unitarie
in quanto si sta usando la matrice di correlazione ovvero si sta
lavorando con variabili standardizzate);
• la quota di varianza spiegata da ogni componente è data dal
rapporto fra il corrispondente autovalore e il totale 7.
Dalla Tab. 3.4.2 e dalla Fig. 3.4.2 vediamo che le prime tre
componenti assorbono oltre l’81% della varianza totale. Anche il
criterio di scelta basato sull’autovalore medio, conduce alla selezione
delle prime tre componenti. Il grado di riduzione è del 43% (=3/7): il
numero di variabili viene più che dimezzato.
Tab. 3.4.2 Porzione di varianza spiegata da ogni componente
Autovalori
Varianza spiegata
Varianza cumulata
Componenti
COMP1
COMP2
COMP3
COMP4
COMP5
COMP6
COMP7
Totale
2.762
1.827
1.098
0.835
0.226
0.172
0.081
7.000
(%)
(%)
39.458
26.098
15.689
11.922
3.226
2.453
1.154
100.000
39.458
65.556
81.245
93.167
96.393
98.846
100.000
L’utilizzo delle prime 3 componenti è soddisfacente anche in termini
di quota varianza spiegata delle variabili originarie, espressa dal
valore della communality R2 (ovvero indice di determinazione lineare
del modello avente come dipendente la variabile originaria e come
Analisi delle concorrenza
37
regressori le 3 componenti) in Tab. 3.4.3. Risultati leggermente
peggiori si ottengono per QUOTA e RS.
3) Interpretazione delle componenti scelte. Nella Tab. 3.4.3 sono state
evidenziate in grassetto le correlazioni più marcate fra componenti e
variabili originarie. In base a questi risultati, possiamo derivare il
significato delle tre componenti.
La prima componente (COMP1) è correlata positivamente con CR,
QR e negativamente con MTCI. Essa sintetizza la situazione
finanziaria di breve e lungo periodo. Valori elevati di COMP1
segnalano situazioni favorevoli; valori bassi situazioni meno
favorevoli (alto indebitamento a lungo e bassa liquidità);
La seconda componente (COMP2) è correlata positivamente con
ROE e ROI. COMP2 sintetizza il livello di redditività. Valori elevati
(bassi) di COMP2 segnalano redditività alta (bassa).
La terza componente (COMP3) presenta le più alte correlazioni con
QUOTA e RS. COMP3 esprime, quindi, la posizione prodottomercato dell’azienda e il potenziale di espansione dell’azienda. Poiché
le correlazioni di COMP3 con QUOTA e RS sono negative, allora
valori elevati di COMP3 indicano basse quote di mercato e bassi
valori di RS, e viceversa.
Fig. 3.4.2 Percentuale di varianza spiegata dalle componenti
100
90
Varianza cumulata (%)
80
70
60
50
40
30
20
10
0
1
2
3
4
Componenti estratte
5
6
7
38
Analisi della concorrenza
Tab. 3.4.3 Correlazione fra variabili e componenti
COMP1
COMP2
COMP3
Variabili
ROE
0.367
0.053
0.875
ROI
0.486
-0.100
0.798
CR
-0.395
0.057
0.874
QR
-0.314
-0.044
0.885
MTCI
0.149
0.196
-0.892
QUOTA
-0.055
0.259
-0.734
RS
-0.215
-0.286
-0.709
R2
0.902
0.883
0.923
0.883
0.856
0.609
0.631
5) Analisi dei dati rispetto alle componenti scelte. La Tab. 3.4.4, in
colonna, presenta i coefficienti (sono gli autovettori della matrice
di correlazione associati ai primi 3 autovalori) che, applicati ai
valori standardizzati delle variabili originarie, forniscono i valori
delle componenti. Tali coefficienti sono scalati in modo che le
componenti principali abbiano varianza unitaria.
Tab. 3.4.4 Coefficienti delle componenti principali
COMP1
COMP2
Variabili
ROE
0.133
0.479
ROI
0.176
0.437
CR
0.316
-0.216
QR
0.320
-0.172
MTCI
-0.323
0.082
QUOTA
-0.020
0.142
RS
-0.078
-0.156
COMP3
0.048
-0.091
0.052
-0.040
0.178
-0.668
-0.646
Ad esempio, il valore di COMP1 per la generica azienda i-esima,
viene calcolato come segue:
COMP1i= 0.133 ROEi*+ 0.176 ROIi*+ 0.316 CRi*+ 0.320 QRi*–
– 0.323 MTCIi*– 0.020 QUOTAi*– 0.078 RSi*
dove l’asterisco sta ad indicare il valore standardizzato della variabile
e non quello originario.
Passando all’analisi grafica dei dati mediante le componenti estratte,
vediamo innanzi tutto la Fig. 3.4.3 che riporta le 52 osservazioni
rispetto ai valori di COMP1 (in ascissa) e COMP2 (in ordinata).
Nel grafico abbiamo evidenziato il punto (0,0) che rappresenta i valori
medi di COMP1 e COMP2. Si individuano così quattro quadranti:
• quadrante di nord-ovest: redditività (COMP2) sopra la media ma
situazione finanziaria (COMP1) inferiore. Qui potrebbero trovarsi,
ad esempio, casi di sfruttamento dell’effetto leva finanziaria.
Analisi delle concorrenza
•
39
quadrante di nord-est: redditività e situazione finanziaria sopra la
media;
• quadrante di sud-est: redditività sotto la media ma situazione
finanziaria sopra;
• quadrante di sud-ovest: redditività e situazione finanziaria sotto la
media. Qui possono trovarsi casi di sofferenza economica e
finanziaria.
La Fig. 3.4.3 mostra un addensamento delle unità piuttosto vicino alla
media. Tuttavia si notano valori abbastanza eccezionali soprattutto
nella parte est. In particolare, i punti del quadrante nord-est segnalano
situazioni particolarmente favorevoli che potrebbero meritare
un’analisi più approfondita e, eventualmente, uno studio di caso
aziendale.
La Fig. 3.4.4 riporta i dati rispetto a COMP3 (in ascissa) e COMP2 (in
ordinata). Abbiamo scelto questa rappresentazione in alternativa a
quella di COMP3 versus COMP1 in quanto appare più interessante
esaminare congiuntamente gli elementi di redditività (contenuti in
COMP2) e di potenzialità di espansione (COMP3).
Lasciamo al lettore l’interpretazione dei quattro quadranti. Ci
limitiamo a notare che la maggior parte dei dati si attesta piuttosto
vicino alla media. Unità estreme che potrebbero essere rappresentative
di qualche situazione da esaminare più a fondo si collocano nel
quadrante sud-ovest e nord-est.
Fig. 3.4.3 Scatter delle osservazioni rispetto alle prime due componenti
4.5
3.5
COMP2
2.5
1.5
0.5
-0.5
-1.5
-2.5
-2
-1
0
1
COMP1
2
3
40
Analisi della concorrenza
Fig. 3.4.3 Scatter delle osservazioni rispetto alla seconda e terza componente
4.5
3.5
2.5
COMP2
1.5
0.5
-0.5
-1.5
-2.5
-4.5
-3.5
-2.5
-1.5
-0.5
0.5
1.5
COMP3
A conclusione di questo capitolo, è importante sottolineare che l’ACP
riveste essenzialmente un ruolo strumentale (la riduzione dei dati)
offrendo una rappresentazione sintetica della struttura di variabilità
delle osservazioni. Le componenti principali hanno unità di misura
(origine degli assi e scala) arbitraria e, quindi, è importante soprattutto
interpretare la forma del grafico, individuando eventuali unità che si
distinguono per la loro posizione. La lettura del fenomeno non finisce
qui: la posizione delle unità di particolare interesse deve essere
interpretata ritornando ai valori delle variabili originarie. Infatti, i
risultati di una ACP dipendono dalla sola struttura di correlazione (di
covarianza) in cui la posizione, in termini assoluti, delle variabili
originarie (ad esempio, l’entità della media aritmetica) viene persa.
Infine, vogliamo far notare che il percorso dello studio è analogo a
quello che, tradizionalmente, viene seguito dall’analista aziendale:
prima si guarda alle variabili di sintesi (che qui sono rappresentate
dalle componenti principali) e successivamente si scende nel dettaglio
esaminando altre grandezze che compongono la stessa variabile di
sintesi.
Previsione insolvenze
4.
41
Analisi statistica multivariata dei dati di bilancio.
Modelli statistici per la previsione delle insolvenze.
Un caso di studio
Introduzione
4.1 Premesse teoriche generali: insolvenza e cause di insolvenza
4.2 Analisi statistica dei bilanci e insolvenza: una breve rassegna
4.3 L’analisi discriminante per lo studio dell’insolvenza
4.4 Un caso di studio
Introduzione
La concessione di prestiti e la gestione del rischio che ne consegue
costituiscono la caratteristica essenziale delle banche e di alcune
tipologie di intermediari finanziari come le società di leasing,
factoring e di credito al consumo.
La fase decisionale che valuta la capacità futura di rimborso del
prestito (capitale e interessi) si basa su un ampio insieme informativo
inerente alle caratteristiche individuali del richiedente (azienda,
soggetto) e alle connotazioni ambientali (es. andamento del settore e/o
della regione) in cui il richiedente opera. L’elaborazione di tali
informazioni mira all’attribuzione (in modo esplicito, implicito,
formalizzato o meno) di una valutazione o punteggio sintetico che
vuole rappresentare la probabilità di rimborso.
Si può ipotizzare che la probabilità di rimborso regolare dei debiti
dipenda da:
1) la capacità reddituale futura dell’impresa (che indichiamo con R);
2) caratteristiche comportamentali del cliente: moralità, sua correttezza personale e volontà di rimborsare regolarmente il prestito
(che indichiamo con C).
La probabilità di rimborso è quindi pensabile come funzione di R e C:
P(rimborso regolare) = F(R,C).
in cui R rappresenta, più che altro, elementi oggettivi mentre C può
risentire anche di fattori soggettivi.
42
Previsione insolvenze
E’ importante osservare che su C può agire direttamente il
finanziatore mettendo in atto tutte quelle misure che hanno lo scopo di
contenere ex ante il rischio di credito (tipo di contratto, richiesta di
garanzie, ecc.). Inoltre, C assume un ruolo relativamente meno
importante nelle aziende organizzate in forma societaria e di grandi
dimensioni, dove le numerose categorie operanti (management, soci,
ecc.) trovano completa convergenza di interessi nella continuazione
della vita dell’impresa Pertanto potremo assumere che:
P(rimborso regolare)≅ f(R)
Elemento fondamentale diventa quindi l’apprezzamento delle
potenzialità di reddito e la valutazione delle condizioni economiche,
finanziarie e patrimoniali dell’impresa, per capire se la concessione
del prestito possa concorrere positivamente alla formazione di reddito
della banca. Pertanto in R vediamo coinvolte le principali misure di
performance aziendali, mentre la specificazione di f può essere
ottenuta ricorrendo ai metodi statistici multivariati, prima fra tutti
l’analisi discriminante. Questa metodologia quantitativa consente di
sintetizzare in un unico indicatore il profilo dell’impresa, espresso
dall’insieme degli indici di bilancio, indicatore che esprime il rischio
di insolvenza.
In questo capitolo viene delineato brevemente lo sviluppo dei modelli
statistici per l’analisi dell’insolvenza e, nell’ultimo paragrafo, viene
presentato un caso di studio. La discussione su alcune teorie che
stanno alla base del fenomeno dell’insolvenza è utile per giustificare
la collocazione dell’analisi prevalentemente a livello micro: il rischio
di insolvenza è ipotizzato generalmente essere funzione delle sole
caratteristiche individuali (indici di bilancio).
Vogliamo precisare che, nel presente capitolo, diamo per scontata la
conoscenza dei vari approcci di analisi discriminante, che viene
spiegata in modo approfondito nella nota metodologica contenuta nel
capitolo 6.
4.1 Premesse teoriche generali: insolvenza e cause di insolvenza
La crisi aziendale è una manifestazione di tipo patologico che può
svilupparsi in più stadi. Cause principali sono fenomeni di squilibrio e
Previsione insolvenze
43
di inefficienza che possono essere di varia natura. Se tali difficoltà
non vengono tempestivamente individuate e affrontate, si ha un
processo di depauperamento delle varie risorse aziendali che, al di là
di certi limiti, esplode nell’incapacità manifesta di fronteggiare gli
impegni assunti e cioè nell’insolvenza.
Il concetto di insolvenza si presta a diversi approcci di analisi che
tengono conto della complessità del sistema aziendale.
a) Insolvenza economica: assenza di redditività e stato di
inefficienza del ciclo produttivo-commerciale (prodotti antiquati,
tecnologie obsolete, rigidità di gestione sono alcune delle cause
più frequenti);
b) Insolvenza finanziaria: problemi di tesoreria, liquidità e rischio di
inesigibilità. Squilibri fra mezzi propri e mezzi di terzi, fra debiti a
breve e a lungo, ecc. sono assai frequenti nelle imprese e, a lungo
andare, possono sfociare in situazioni di insolvenza. L’insolvenza
finanziaria è più facilmente rilevabile attraverso indicatori di
rapida consultazione quali, ad esempio, il Bollettino Ufficiale dei
Protesti.
c) Insolvenza giuridica. Il fallimento è la constatazione giuridica
dell’insolvenza finanziaria e rappresenta lo strumento col quale il
legislatore dichiara la crisi aziendale e garantisce i diritti dei terzi.
Nei casi di crisi reversibile, il legislatore ha previsto lo strumento
di amministrazione controllata.
Data la complessità con cui si può manifestare, il fenomeno
dell’insolvenza può avere cause molteplici. La letteratura economicoaziendale ha individuato varie tipologie di cause che possono minare
l’equilibrio aziendale. Esse vengono generalmente classificate
secondo due criteri:
A) in base al rapporto temporale fra origine della causa e
manifestazione dell’insolvenza: cause remote o prossime;
B) in base all’ambiente di origine della cause: cause esterne o
interne.
In merito al punto A), cause remote sono da ricercare in squilibri e
inefficienze strutturali e cioè aventi natura di lungo termine.
Incapacità del management, cattiva qualità del sistema informativo
(relativamente al controllo budgetario, ai processi di
programmazione), stile direzionale troppo rigido, squilibri nelle
competenze possono costituire esempi di cause remote. Nelle medie e
piccole imprese, il vertice imprenditoriale coincide molto spesso con
44
Previsione insolvenze
l’assetto proprietario e riassume in sé tutte le funzioni aziendali,
spesso senza poter maturare la giusta competenza nelle varie aree. La
limitata esperienza in materia di gestione, costituiscono una grave
minaccia per la vita dell’azienda.
La classificazione del punto B) distingue fra cause derivanti da scelte
imprenditoriali sbagliate e cause dovute a forze e fenomeni che
sfuggono al dominio degli uomini dell’impresa. Tuttavia accade che,
in pratica, neppure mediante uno studio di caso aziendale si riesce a
individuare le corrette interazioni fra i due tipi di cause.
Certamente la crisi di impresa risulta legata anche all’andamento del
ciclo economico (aspetti congiunturali dell’economia) e a cicli di
settore. Ad esempio, con riferimento agli ultimi 30 anni, i principali
processi di mutamento ambientale che hanno influenzato lo stato di
salute delle imprese sono:
1) variazioni spaziali dei livelli di costo del lavoro che hanno
favorito i paesi emergenti dell’Asia orientale;
2) i prezzi del petrolio e delle materie prime che hanno subito
improvvise impennate negli anni 1973 e 1985;
3) alta instabilità dei cambi valutari che ha agito con effetti
altalenanti sui prezzi dei beni destinati all’esportazione;
4) rapidi processi innovativi e accelerazione dell’evoluzione tecnica;
5) fenomeno inflazionistico.
Fra le cause interne, gli errori gestionali più ricorrenti che possono
compromettere l’equilibrio aziendale riguardano un eccessivo
sviluppo del fatturato non accompagnato da un adeguato apporto di
capitali permanenti. Questa situazione può degenerare in una crisi se,
all’aumentare del fatturato e del conseguente fabbisogno di capitale
circolante, salgono i prestiti bancari e con essi gli interessi passivi, ma
non crescono allo stesso tempo liquidità, capitale proprio e profitto.
Relativamente alle imprese minori che, nel nostro paese,
rappresentano circa il 90% del totale, tre sono i punti problematici: (i)
il livello di cultura del vertice imprenditoriale; (ii) le difficoltà di
accesso alle vie dell’aumento del capitale di rischio; (iii) le difficoltà
di accesso al credito a medio-lungo termine, col rischio di
sbilanciamento della struttura finanziaria verso il credito bancario a
breve. L’incidenza dei finanziamenti a breve sulle passività totali è di
circa 39% per le piccole e medie aziende (secondo la classificazione
Istat: aziende con meno di 20 addetti) contro il 19% delle grandi.
Previsione insolvenze
45
4.2 Analisi statistica dei bilanci e insolvenza: una breve rassegna
Per valutare in maniera completa ed esauriente lo stato di salute di
un’impresa, è necessario compiere un’analisi che tenga conto delle
numerose variabili qualitative (strategie, qualità del management,
ecc.) e quantitative (dati di bilancio, dati macroeconomici e/o di
settore) che la caratterizzano.
In particolare, l’analisi basata sugli indici di bilancio costituisce
l’elemento fondamentale dell’approccio più recente alla modellazione
del rischio di insolvenza. Il contributo dell’analisi statistica in questo
senso può avere:
1) scopi descrittivi ed esplicativi di come si manifesta e si sviluppa
una crisi aziendale. Da questa analisi è possibile risalire alle cause
che hanno agito nel determinare lo stato di insolvenza;
2) scopi predittivi: costruzione di un modello che valuti il rischio
associato ad una data struttura di ratio di bilancio. Questo
approccio di studio può identificare quegli indici di bilancio
maggiormente significativi a diagnosticare precocemente
situazioni di crisi.
I primi studi statistici sull’insolvenza aziendale, sono stati condotti
negli anni 30, in U.S.A., ad opera di vari autori soprattutto
statunitensi. Fino algli anni 60, si è trattato prevalentemente di analisi
statistiche univariate dei ratio di bilancio, che si proponevano
principalmente di rispondere ai seguenti quesiti:
• quale indice, in base ai valori assunti in esercizi precedenti, è in
grado di prevedere con congruo anticipo la manifestazione di
insolvenza ?
• in un campione di imprese reali, quali sono gli indici di bilancio
che, più degli altri, presentano distribuzioni diverse fra le imprese
sane e fra le imprese insolventi ?
Riportiamo, brevemente, i risultati di uno studio condotto da Beaver
nel 1966 (cfr. Foster, 1986). Avvalendosi di 79 imprese sofferenti
(poiché incorse, nel periodo 1954-64, in uno dei seguenti fenomeni:
fallimento, mancato pagamento di obbligazioni in scadenza, mancato
pagamento dei dividendi sulle azioni privilegiate), ed un gruppo di 79
imprese sane, il Beaver ha determinato la capacità di alcuni indici di
bilancio, nel segnalare precocemente situazioni di crisi, attraverso due
tecniche:
46
Previsione insolvenze
1) l’analisi dei profili temporali: esame dell’andamento rispetto al
tempo, dei valori medi dell’indice (riferiti a periodi precedenti
l’insolvenza) calcolati all’interno dei due gruppi di imprese;
2) il calcolo del valore critico (cut off) dell’indice che separa meglio
il gruppo delle aziende sane da quello delle aziende insolventi. La
capacità predittiva dell’indice è valutata in base al tasso di errore
commesso nel riclassificare, mediante i valori dell’indice, le
aziende nei due gruppi originari.
L’analisi dei profili consente di rilevare che le medie di alcuni indici
hanno andamenti molto differenziati per i due gruppi di imprese. Tale
differente comportamento si evidenzia già alcuni anni prima l’evento
di insolvenza. Nelle figure seguenti sono rappresentati, a titolo di
esempio, gli andamenti di due indici ripresi da Foster (1986). Le due
spezzate rappresentano le medie degli indici per i 5 anni precedenti
l’insolvenza.
Redd.netto/Tot. attivo
0,2
0,1
Sane
0
-0,1
5
4
3
2
1
Insolventi
-0,2
Anni precedenti l'insolvenza
Tot. Debiti/Tot. passivo
0,8
0,6
Sane
0,4
Insolventi
0,2
5
4
3
2
1
Anni precedenti l'insolvenza
Previsione insolvenze
47
In base al criterio 2), Beaver classificò in ordine crescente i valori
assunti da ognuno degli indici di bilancio per tutte le aziende (sia il
gruppo delle insolventi sia quello delle sane). Per ogni indice calcolò
il miglior punto critico (punto di cut-off) che consentiva la migliore
riclassificazione delle imprese del campione, nel proprio gruppo di
appartenenza. Le operazioni per questa analisi sono quindi:
1) ordinare in senso crescente (o descrescente) i valori del ratio;
2) individuare un valore intermedio k che ripartisce le unità in due
set: le unità con valori del ratio inferiori a k e quelle unità con
valori superiori;
3) si verifica se tale valore intermedio può essere utilizzato per
classificare le unità nei due gruppi originali. Se, ad esempio, si
decide che tutte le unità con valore del ratio inferiore a k siano da
ritenersi insolventi, si costruisce la seguente tabella di
classificazione in base alla quale è possibile calcolare la
percentuale totale di errata classificazione che è pari a
100(n01+n10)/n.
Gruppi
veri
Sane
Insolventi
Gruppi assegnati
ratio<k
ratio≥k
(Insolventi)
(Sane)
n00
n01
n10
n11
Totale
n0
n1
4) il migliore punto di cut-off per un dato indice di bilancio, sarà quel
valore per il quale si ottiene la minore percentuale di errata
classificazione.
A titolo di esempio riportiamo i risultati ottenuti da Beaver per i due
indici rappresentati nelle figure precedenti, esaminando i dati di
bilancio relativi agli anni precedenti la crisi.
Tab. 4.2.1 Errori percentuali di classificazione
Indici
Anni precedenti l’insolvenza
5
4
3
2
Redd.netto/Tot.attivo
28
29
23
21
Tot.debiti/Tot.passivo
28
27
24
25
1
13
19
Fonte: Foster (1986)
L’analisi condotta da Beaver mostrò che alcuni indici di bilancio
(soprattutto quelli di liquidità e di indebitamento) sono capaci di
48
Previsione insolvenze
segnalare precocemente lo stato di crisi dell'azienda. Inoltre col
criterio del cut off, è possibile proporre una regola di classificazione
sulla base del valore dell’indice di bilancio.
Da questo studio vediamo una peculiarità comune alle ricerche
sull’insolvenza: l’impiego di dati retrospettivi. Infatti, individuata la
crisi aziendale al tempo t, vengono analizzati i dati di bilancio riferiti
ad un anno (o più anni) precedente sia per le imprese insolventi al
tempo t sia per quelle sane al tempo t, queste ultime usate come
termine di confronto. Il procedimento appare coerente con
l’impostazione descritta nell’introduzione: il modello statistico
avrebbe infatti lo scopo di prefigurare lo stato di salute futuro
dell’azienda.
Il limite principale dell’approccio univariato al rischio di insolvenza è
quello di considerare ogni singolo indice separatamente dagli altri
mentre, come suggerito anche dall’economia aziendale, gli indici
sono espressione delle diverse dimensioni del sistema aziendale che
sono interconnesse.
Lo studio separato dei vari indici conduce anche a difficoltà
interpretative in quanto i vari quozienti spesso danno responsi
divergenti sulla situazione dell’impresa (una medesima azienda
potrebbe risultare classificata nel gruppo delle fallite in base ad un
indice e nel gruppo delle sane in base ad un altro indice) rendendo
difficile una sua valutazione globale.
Per la verità, già prima degli anni 60, ci sono stati dei tentativi di
costruzione di un punteggio sintetico, mediante medie aritmetiche
ponderate di indici di bilancio (cfr. la rassegna in Teodori, 1989).
Tuttavia, in tali contributi, i pesi attribuiti ai vari indici risentono di
elementi di natura soggettiva. Inoltre, tale media ponderata non tiene
conto delle eventuali interrelazioni (correlazioni) esistenti fra gli
indici.
Mediante l’analisi statistica multivariata è possibile valutare in senso
globale, attraverso un gran numero di indici di bilancio considerati
simultaneamente, la situazione economico-finanziaria dell’impresa e
di sintetizzare questa valutazione in modo da facilitare
l’interpretazione dei risultati e favorire il loro confronto.
Previsione insolvenze
49
A partire dalla fine degli anni 60, i lavori basati su metodologie di
natura multidimensionale sono divenuti sempre più numerosi. La
metodologia più utilizzata è l'analisi discriminante (AD) lineare1.
L’AD lineare è stata utilizzata per la prima volta da Altman (1968;
1983), il quale ha ricavato il cosiddetto modello Z-score (si tratta del
punteggio della funzione discriminante).
I risultati ottenuti furono di gran lunga migliori di quelli di Beaver e il
modello riscosse in breve tempo un notevole successo sia sul piano
teorico sia su quello pratico, aprendo la strada a numerosi lavori.
Accanto alla tecnica della AD, altre metodologie sono state impiegate
per affrontare il problema della previsione delle crisi aziendali. Ad
esempio, l’AD è stata applicata sulle componenti principali ricavate
da un insieme di indici, in modo da ridurre l’analisi ad un minore
numero di indicatori (cfr. Rossi, 1984). Più recentemente è stata usata
l’analisi discriminante logistica per la previsione delle crisi delle
banche (Cannari e Signorini, 1995).
Nonostante gli ampi margini di miglioramento ancora possibili, alcuni
di questi modelli hanno raggiunto risultati così notevoli da essere
ormai ritenuti strumenti indispensabili anche nella pratica aziendale.
A dimostrazione della validità operativa raggiunta dalla metodologia
in questione, la Centrale dei Bilanci (costituita dalla Banca d’Italia e
dall’ABI) ha predisposto per le banche uno strumento basato su
funzioni discriminanti per la rapida identificazione delle imprese che
si trovano in una difficile situazione economico-finanziaria.
Rimandiamo alla nota metodologica (capitolo 6) per la descrizione
della tecnica AD. In questa sede esaminiamo le fasi per la costruzione
di un modello per la previsione delle insolvenze e uno studio di caso.
4.3 L’analisi discriminante per lo studio dell’insolvenza
Lo schema seguente mostra le principali fasi per costruzione di un
modello di previsione delle insolvenze basato sull’AD.
1 Tali modelli di previsione delle insolvenze sono detti anche credit scoring
adottando una interpretazione estensiva di questo termine rispetto a quanto avviene
negli studi anglosassoni dove tale termine è utilizzato per indicare i modelli di
finanziamento del credito al consumo.
50
Previsione insolvenze
Fig. 4.3.1 Fasi per la costruzione di un modelli di analisi discriminante
Definizione del
gruppo delle
imprese fallite
Teorie delle
cause di
insolvenza
Criteri di
omogeneità
Definizione del
gruppo delle
imprese sane
Criteri di
‘bilanciamento’
Scelta dei ratios
Controllo dati
contabili
Riclassificazioni
di bilancio
Stima della funzione
discriminante
Verifica dell’accuratezza classificatoria
• analisi interne
• analisi esterne
Interpretazione della funzione
• correlazioni
Regola classificatoria
Il modello di AD per la previsione dell’insolvenza è generalmente una
funzione dei soli ratio di bilancio e, pertanto, si propone di
sintetizzare in un unico valore (o punteggio, score) lo stato di salute
di un’azienda.
Poiché si tratta di un modello di previsione, esso è stimato da dati
retrospettivi. Se si tratta di dati precedenti h anni la crisi di
insolvenza, il modello, applicato ad aziende in vita, si propone di
stimare precocemente (h anni prima) tale crisi.
Previsione insolvenze
51
I principali problemi, di natura statistica, che si devono affrontare per
la conduzione di una AD al fine di predisporre un modello per la
previsione delle insolvenze aziendali, sono i seguenti:
1)
2)
3)
4)
5)
6)
la definizione dei gruppi
la composizione e formazione del campione
la selezione delle variabili
la distribuzione dei ratios aziendali
il criterio classificatorio
i costi di errata classificazione
1) La definizione dei gruppi.
Uno dei presupposti dell’impiego dell’AD è che esista una differenza
fra le due popolazioni di aziende: quella delle aziende sane e quella
delle fallite. Le popolazioni di riferimento possono essere costituite
dal portafoglio prestiti di un’azienda di credito, dalle aziende di un
determinato settore di attività economica, di un comparto produttivo,
ecc. Determinata la popolazione di riferimento, è necessario trovare
un criterio in base al quale si individuano, all’interno di essa, i due
gruppi di aziende.
Il criterio più frequentemente utilizzato è la dichiarazione di
fallimento. Individuate le aziende fallite ad un determinato periodo t,
si definisce in corrispondenza (secondo dei criteri che vedremo più
avanti) la popolazione di aziende sane. Allo scopo di costruire modelli
di previsione, verranno utilizzati dati di bilancio riferiti ad un anno (o
più) precedente il fallimento.
Un’alternativa può essere quella di dichiarare insolvente o anomala
l’impresa dichiarata insolvente all’Anagrafe Centrale dei Rischi della
Banca d’Italia.
Se ci basiamo sul portafoglio crediti di un’azienda di credito, si
definiscono insolventi le aziende che, avendo ottenuto un prestito, non
lo hanno poi rimborsato. Il portafoglio crediti, tuttavia, contiene solo
le imprese affidate e non tiene conto delle caratteristiche di quelle che
non sono state giudicate meritevoli di prestito. L’AD condotta su
questo tipo di dati produce dei risultati difficilmente generalizzabili.
Anche la definizione di impresa sana è abbastanza incerta.
Un’impresa in attività non è un dato sufficiente per affermare che essa
si trovi in equilibrio economico finanziario. Conseguenze di tali
52
Previsione insolvenze
incertezze sono l’incapacità discriminatoria della AD in quanto i due
gruppi di aziende non sono ben distinti rispetto ai valori dei ratio.
E’ bene precisare che, solitamente, un modello di AD è costruito per
una tipologia abbastanza omogenea di aziende (es. manifatturiere del
settore tessile). Infatti, la letteratura mostra prestazioni migliori per i
modelli cosiddetti ‘di settore’, rispetto a modelli riferiti da imprese
più eterogenee.
2) Composizione e formazione del campione
In generale, il numero di aziende fallite è relativamente limitato. Per
ottenere una numerosità statisticamente adeguata, alcuni autori hanno
dovuto cumulare i fallimenti verificatisi in più periodi di tempo
(anni). Il raggruppamento delle aziende fallite può presentare un
grave inconveniente: alcuni quozienti di bilancio possono subire nel
corso degli anni notevoli variazioni, a causa di diversi fattori come
l’inflazione, mutamenti tecnologici ecc. Considerare bilanci che sono
troppo distanti nel tempo può creare disomogeneità nei dati.
La scelta delle aziende sane viene generalmente condizionata alla
composizione del gruppo di aziende fallite. Si ritiene, infatti, che i due
gruppi di imprese debbano rispettare determinati criteri di
omogeneità. Si parla di procedure di bilanciamento o appaiamento
che, talvolta, possono richiedere dei procedimenti specifici per la
conduzione di un’analisi statistica.
I principali criteri di bilanciamento sono basati sulle seguenti
caratteristiche aziendali.
a) L’oggetto sociale e/o stesso settore di appartenenza;
b) La dimensione aziendale. Il fattore dimensionale influisce sulla
propensione al fallimento come esposto nel primo paragrafo. Le
dimensioni aziendali sono solitamente misurate dall’ammontare
del capitale investito, dal fatturato, dal numero dei dipendenti;
c) La forma giuridica. Alle varie forme giuridiche corrispondono
diversi gradi di responsabilità e diverse composizioni dei soggetti
apportatori di capitale, che possono influire in modo rilevante
sulla struttura finanziaria e patrimoniale delle aziende.
d) L’età dell’azienda. E’ stata empiricamente verificata la maggior
propensione a fallire delle imprese relativamente più giovani.
Per capire meglio quanto detto si fa il seguente esempio. Poiché l’età
dell’azienda può influenzare la propensione all’insolvenza, se i due
gruppi di aziende sono diversi rispetto all’età, si rischia di attribuire
Previsione insolvenze
53
agli indici di bilancio coinvolti nella AD, anche quegli effetti
discriminatori che sono dovuti alla differenza dell’età media dei due
gruppi.
Concludendo, il campione ha generalmente un disegno stratificato
(rispetto all’evento insolvenza/non insolvenza) con frazione di
campionamento diversa per i due gruppi di aziende: le sane e le fallite
(spesso il campione delle fallite contiene l’intera sottopopolazione)
3) Selezione delle variabili.
Dall’esame della letteratura si possono riscontrare tre tipologie di
variabili inserite nei modelli di insolvenza: a) indici di bilancio; b)
variabili derivate dagli indici di bilancio; c) variabili a livello macro.
La tipologia prevalente è quella degli indici di bilancio. L’impiego di
questi richiede di affrontare le seguenti problematiche.
• Valutazione dell’effetto distorsivo delle politiche di bilancio o
window dressing operations sul modello di insolvenza.
Specialmente nel contesto italiano dove il bilancio è fortemente
fiscal driven occorre prestare attenzione a quelle poste di bilancio
nelle quali si annidano sottovalutazioni (sopravvalutazioni) di
elementi reddituali o patrimoniali positivi (negativi).
• Effetti distorsivi del cambiamento di potere di acquisto della
moneta sui valori di bilancio. Su questo punto l’evidenza empirica
ha mostrato che l’impiego di dati rettificati rispetto a quelli a
valori correnti, non comporta né miglioramenti né peggioramenti
significativi. Si preferisce non ricorrere alla rettifica in quanto
questa operazione può introdurre ulteriori incertezze senza
apprezzabili vantaggi.
• La capitalizzazione o meno dei beni in locazione finanziaria. E’ a
partire dagli anni 80 che è iniziato un sempre maggior ricorso a
questa forma di finanziamento. Su questo punto l’opinione dei
vari autori è abbastanza discorde.
Fra le variabili derivate dagli indici di bilancio (tipologia b),
troviamo:
• il trend degli ultimi anni (es. l’andamento del ROE, ecc.) che
spesso viene espresso mediante il coefficiente angolare della retta
di regressione della serie storica rispetto al tempo;
• la variabilità osservata negli ultimi anni (ad es. del ROE, del
current ratio, ecc.). Questa viene generalmente espressa dalla
varianza della serie storica;
54
Previsione insolvenze
•
i market based ratio: si tratta di indici derivati dall’informativa di
bilancio che hanno al numeratore la grandezza individuale e al
denominatore l’aggregato dell’insieme delle aziende. Un esempio
è costituito dalla quota di mercato.
Fra le variabili (tipologia c) di livello macro (settore, economia
nazionale, ecc.), i modelli di previsione delle insolvenze hanno visto
l’impiego dell’indice generale dei prezzi al consumo e dell’indice
generale della produzione industriale.
Poiché gli indici di bilancio sono le variabili maggiormente utilizzate,
vogliamo fare ulteriori considerazioni in merito.
La scelta degli indici di bilancio deve essere condotta sulla base di
teorie dell’insolvenza, studi ed esperienze maturate. La selezione può
essere suggerita anche dagli specifici obiettivi perseguiti nello studio.
Ad esempio, nello sviluppare modelli per le piccole e medie imprese,
si dovrebbero scegliere quegli indici di bilancio che risentono meno
delle manipolazioni contabili, si dovrebbe tenere conto del minore
contenuto informativo di alcune poste di bilancio, ecc.
Successivamente alla stima della funzione discriminante è possibile
valutare il contributo di ogni singola variabile alla previsione
dell’insolvenza. Non conviene affidare la scelta degli indici di
bilancio esclusivamente a procedure automatiche contenute in
pacchetti statistici (es. le procedure di tipo stepwise).
Dall’analisi dei principali modelli di previsione delle insolvenze
aziendali, si individua (Teodori, 1989) la prevalenza degli indici di
liquidità. Le ragioni vanno ricercate sia nel fatto che la liquidità è la
dimensione strutturale più analizzata da quando si sono sviluppate le
analisi di bilancio sia perché non pochi autori inquadrano il fallimento
come fenomeno cash-oriented. Gli indici di struttura finanziaria a
lungo termine sono riscontrabili in modo particolare nei modelli
italiani, segno di una maggiore attenzione ad archi temporali di
dimensione più ampia.
4) La distribuzione dei ratio aziendali.
Come esposto nella nota metodologica, l’AD normale presuppone la
distribuzione normale multivariata delle variabili che, nel nostro caso,
sono gli indici di bilancio. Vogliamo precisare che qui si intende la
normalità della distribuzione congiunta delle variabili, e non (solo) la
normalità della distribuzione del singolo indice di bilancio
(distribuzione marginale). Tuttavia, poiché la normalità congiunta
Previsione insolvenze
55
implica quella marginale, una verifica empirica può essere
ragionevolmente condotta anche mediante un’analisi univariata.
Come già esposto nei capitoli precedenti, le distribuzioni statistiche
degli indici di bilancio sono caratterizzate da asimmetria e curtosi. Si
tratta in genere di situazioni difficilmente riconducibili all’ipotesi di
normalità. Di fatto, la verifica della condizione di normalità è stata
quasi sempre elusa dalla maggior parte degli studiosi che hanno
utilizzato l’AD normale.
Tuttavia, alcuni autori (v. la rassegna in Maddala, 1983) hanno
verificato un buon funzionamento della AD normale lineare anche nei
casi in cui le ipotesi sulla normalità e sull’uguaglianza delle matrice
di varianza e covarianza dei gruppi non sono soddisfatte. Inoltre,
l’AD normale lineare può trovare una sua giustificazione autonoma in
base ad una interpretazione geometrica. Infatti, l’uso del criterio
classificatorio basato sulla verosimiglianza massima equivale a quello
basato sulla distanza di Mahalanobis (al quadrato) fra la singola unità
e il centroide del gruppo.
Vogliamo infine osservare che l’impiego dell’AD logistica sarebbe
comunque corretto in quanto non richiede alcuna ipotesi distributiva
sui ratio di bilancio.
5) Il criterio classificatorio.
La scelta fra criterio della verosimiglianza massima e criterio della
massima probabilità a posteriori è connesso con:
1) la conoscenza o meno delle probabilità a priori (questa
informazione giuoca un ruolo diverso a seconda che si tratti di AD
normale e AD logistica).
2) l’accuratezza classificatoria relativa ai due gruppi.
Poiché la proporzione dei due gruppi nella popolazione è
marcatamente diversa, l’uso del criterio della massima probabilità a
posteriori favorisce l’accuratezza classificatoria del gruppo più
numeroso (sane) penalizzando quella del gruppo più piccolo
(insolventi). Viceversa, l’utilizzo di uguali probabilità a priori
consente una più corretta classificazione delle unità appartenenti al
gruppo di numerosità minore.
Dalle considerazioni qui svolte, si capisce che l’impiego di probabilità
a priori uguali o diverse è connesso anche con i costi di errata
classificazione che vengono discussi nel punto 5.
56
Previsione insolvenze
In ogni caso, al momento dell’impiego del modello a fini predittivi,
l’informazione sulle probabilità a priori è da intendersi riferita a tempi
futuri e, quindi, anche questa dovrebbe scaturire da un modello di
previsione.
5) I costi di errata classificazione.
I due tipi di errore di classificazione che possiamo commettere con un
modello di analisi discriminante sono:
a) classificare un’impresa sana come insolvente (falso positivo);
b) classificare un’impresa insolvente come sana (falso negativo).
I due tipi di errore non hanno associati costi equivalenti. La diversità
dei costi dipende dagli obiettivi che si perseguono con la costruzione
di un modello di previsione delle insolvenze.
Altman definisce il costo di un falso negativo (FN) come:
Costo(FN)= 1–(a+b)/ft
dove: a : somma riscossa prima della crisi di insolvenza
b : somma riscossa successivamente alla crisi di insolvenza
ft : ammontare del prestito erogato fino a 12 mesi precedenti il
mancato rimborso.
Il costo associato ad un falso positivo (FP) è, secondo lo stesso
autore:
Costo(FP)= r–i
dove r: tasso di interesse sul prestito rifiutato
i: tasso di interesse su investimenti alternativi possibili.
(generalmente si considera il tasso minimo, riferito ad un
investimento a bassissimo di rischio (es. titoli pubblici).
La stima dei costi così definiti, effettuata da Altman, ha mostrato che
Costo(FN) era circa 31 volte il Costo(FP). Pertanto, nella valutazione
della capacità predittiva della funzione discriminante, è opportuno
tenere conte anche di questo aspetto. Ad ogni modo, stando a questi
Previsione insolvenze
57
risultati, sembra da preferire una più corretta classificazione del
gruppo delle aziende insolventi e cioè del gruppo meno numeroso2.
4.4 Un caso di studio
Nell’esposizione dello studio di caso e nella costruzione del modello,
seguiremo le fasi fondamentali rappresentate nella Fig. 4.3.1. In
breve, l’elaborazione del modello ha affrontato i seguenti punti:
1) formazione di un campione di imprese insolventi e di un campione
di imprese in vita;
2) riclassificazione dei bilanci e calcolo, per ciascuna impresa, di
alcuni indici di bilancio, scelti in base alla letteratura
sull’argomento;
3) analisi multivariata del rischio di insolvenza mediante l’AD
normale lineare: stima della funzione discriminante e valutazione
della sua capacità classificatoria.
Poiché l’esposizione ha finalità didattiche, ci limiteremo a considerare
un ridotto numero di indici di bilancio e un limitato gruppo di
aziende, circoscrivendo l’analisi rispetto al settore produttivo e alla
località geografica. E’ bene chiarire che, nella pratica applicativa, è
necessario avere a disposizione un numero di osservazioni superiore a
quello qui utilizzato, ai fini della validità generale del modello.
Oggetto di analisi sono aziende operanti nel settore manifatturiero
dell’abbigliamento e biancheria, in una provincia toscana. L’obiettivo
è quindi quello di costruire un modello di tipo ‘settoriale’ che ha il
vantaggio di riferirsi a unità relativamente omogenee anche in termini
di struttura economico-patrimoniale. Sempre per l’esigenza di
lavorare con dati omogenei, facciamo riferimento alle sole società di
capitale.
Il primo passo per la formazione del set di dati riguarda il gruppo
delle imprese fallite. Dalla consultazione dei dati disponibili presso la
Camera di Commercio della provincia, sono state desunte le seguenti
informazioni: 1) nel 1995 sono fallite 11 aziende; 2) nel 1996 sono
fallite 13 aziende.
2 E’ importante osservare che i costi di errata classificazione possono essere
direttamente inseriti nella AD applicando la regola classificatoria che minimizza il
costo atteso di errata classificazione. Questo procedimento non viene descritto nella
nota metodologica ma può essere trovato, ad esempio, in Huberty (1994).
58
Previsione insolvenze
A causa dell’esiguo numero di casi, è necessario cumulare le unità
relativi ai due anni. Inoltre, poiché oggetto di analisi è l’informativa
di bilancio precedente l’evento del fallimento, si sono utilizzati i dati
relativi al: 1992, per le imprese fallite nel 1995; 1993, per le imprese
fallite nel 1996. Lo sfasamento fra 1) e 2) è talmente breve che non
dovrebbero sussistere problemi di eterogeneità nei dati contabili.
Purtroppo non tutti i bilanci si sono rivelati utili. Ad esempio, alcune
delle imprese erano, nell’anno precedente il fallimento, già in
liquidazione. Il numero di aziende si è ridotto a 10, come riportato
nella Tab. 4.4.1.
Pur nella sua estrema limitatezza (in termini di numero di unità), la
tabella conferma quanto accennato nel paragrafo 4.1: si nota, infatti,
la presenza di aziende di costituzione piuttosto recente.
Tab. 4.4.1 Gruppo delle aziende fallite
Azienda
Anno
Anno
Capitale investito
fallimento costituzione (1994; 1000 L.)
A
1995
1991
168630
B
1995
1982
301840
C
1995
1978
432174
D
1995
1980
8756181
E
1995
1990
433015
F
1995
1991
129519
G
1996
1989
3964945
H
1996
1988
1447377
I
1996
1991
1423887
L
1996
1993
571897
Anno
riferimento dati
1992
1992
1992
1992
1992
1992
1993
1993
1993
1993
La Tab. 4.4.2 mostra il campione di imprese sane che è stato scelto in
modo da garantire una certa comparabilità con quello delle imprese
fallite, rispetto alle caratteristiche rappresentate in Tab. 4.4.1.
Previsione insolvenze
Tab. 4.4.2 Gruppo delle aziende sane
Azienda
Sana al:
Anno
Capitale investito
costituzione (1994; 1000 L.)
1
1995
1991
469760
2
1995
1982
1249125
3
1995
1988
380977
4
1995
1980
789832
5
1995
1989
256722
6
1995
1991
316754
7
1996
1989
1028442
8
1996
1986
2246773
9
1996
1991
876546
10
1996
1987
1266734
59
Anno
riferimento dati
1992
1992
1992
1992
1992
1992
1993
1993
1993
1993
Il nostro set di dati è pertanto costituito, seguendo l’indicazione della
maggior parte degli studi, da due gruppi di uguale dimensione, senza
riprodurre nel campione la proporzione esistente fra aziende sane e
fallite nella popolazione di riferimento.
Riguardo agli indici di bilancio scelti, ci limitiamo ai 4 seguenti:
•
•
•
•
CR: attività correnti/passività correnti (current ratio)
DP: tot. debiti/tot. passivo
ROA: reddito operativo/tot. attivo
RD: fatturato/tot. debiti
dove ‘tot. debiti’ indica l’intero indebitamento verso terzi (sia a lungo
sia a breve). La Tab. 4.4.3 contiene i dati relativi ai quattro indici di
bilancio scelti.
60
Previsione insolvenze
Tab. 4.4.3 Indici di bilancio (gruppo 0: aziende sane; gruppo 1: aziende fallite)
Azienda
Gruppo
CR
DP
ROA
FD
A
1
0.9576
0.9026
–0.3361
0.6426
B
1
0.7388
1.2028
–0.4035
1.5987
C
1
1.0195
0.9717
0.0902
0.7758
D
1
1.0936
0.8745
0.0900
2.1710
E
1
0.8431
0.9807
0.0136
0.1211
F
1
1.1011
0.8679
0.0345
1.0276
G
1
1.0888
1.0075
0.0410
1.2385
H
1
1.5878
0.9575
–0.0211
2.1222
I
1
1.4209
0.9628
0.0697
1.1224
L
1
0.2549
1.3125
–0.0577
0.0246
1
0
1.2023
0.7730
0.0459
2.0869
2
0
0.9212
0.9748
–0.0055
1.6454
3
0
1.7112
0.7804
0.0889
2.5122
4
0
1.1822
0.9654
0.0272
1.4345
5
0
1.2891
0.9271
0.0939
1.5814
6
0
0.7961
0.9526
0.0644
0.1337
7
0
1.1060
0.9832
0.0858
1.3553
8
0
1.2271
0.9694
0.0604
1.6252
9
0
0.9627
1.0300
0.0124
0.7690
10
0
1.1090
0.8402
0.0558
1.0703
La tabella seguente mostra alcune caratteristiche distributive dei dati
relativi ai due gruppi. In particolare si nota il valore negativo della
media di ROA per il gruppo delle fallite che registra, mediamente,
una minore liquidità (CR), più basso indice di rotazione (FD) e
maggiore indebitamento (FD). Dagli indici di asimmetria e curtosi, si
può inoltre notare una moderata deviazione dalla normalità3.
Tab. 4.4.4 Indici statistici dei dati di Tab. 4.4.3
Ratio
Gruppo 1: fallite
Media
Var. Asimm Curtosi Media
.
CR
1.011
0.133 –0.552
1.467
1.151
DP
1.004
0.021
1.463
1.479
0.920
ROA
–0.048
0.031 –1.525
1.027
0.053
FD
1.084
0.543
0.118 –0.798
1.421
Gruppo 0: sane
Var. Asimm Curtosi
.
0.062
1.036
2.359
0.008 –0.836 –0.731
0.001 –0.488 –0.733
0.440 –0.399
0.800
3 La verifica dell’ipotesi di normalità (marginale) può essere controllata anche
tramite un normal probability plot. Tuttavia, data l’esiguità dei dati (infatti
bisognerebbe costruire il grafico separatamente per gruppo), tralasciamo questo tipo
di analisi.
Previsione insolvenze
61
La matrice di varianza e covarianza within (pooled) W è4:
0.0879
0.0129
− 0.0234
W =
0.0120 − 0.0048 0.0145
0.1392 − 0.0323 0.0041 0.4427
e la distanza di Mahalanobis al quadrato dij di ogni unità i-esima
(i=1,2,…,20) dal centroide del gruppo j-esimo (j=0,1) è stimata come:
dij = (xi–mj)W–1(xi–mj)’
L’applicazione del metodo della verosimiglianza massima (con
matrice di covarianza uguale nei due gruppi) equivale a collocare
l’unità nel gruppo col centroide più vicino. I risultati ottenuti sono
presentati nella Tab. 4.4.5.
Tab. 4.4.5 Riclassificazione delle unità (distanza di Mahalanobis al quadrato)
Discriminant
Azienda
Gruppo
Distanza dal Distanza dal
Gruppo*
**
score Z1
assegnato
centroide 0 centroide 1
A
1
14.440
10.31340
1
2.0644
B
1
15.511
10.17260
1
2.6700
C
1
1.123
1.44482
0
–0.1599
D
1
4.314
8.16350
0
–1.9232
E
1
3.861
2.70357
1
0.5795
F
1
1.040
1.94271
0
–0.4505
G
1
0.807
0.69733
1
0.0562
H
1
6.060
5.01925
1
0.5223
I
1
5.392
4.24364
1
0.5757
L
1
11.600
8.56528
1
1.5179
1
0
4.317
8.05411
0
–1.8673
2
0
1.989
3.33157
0
–0.6702
3
0
3.439
5.92591
0
–1.2415
4
0
0.469
0.58959
0
–0.0590
5
0
0.552
1.68914
0
–0.5674
6
0
3.711
3.76116
0
–0.0242
7
0
0.572
1.43902
0
–0.4324
8
0
0.748
1.39211
0
–0.3205
9
0
1.558
0.52944
1
0.5153
10
0
1.379
2.90503
0
–0.7619
* criterio della verosimiglianza massima; ** v. espressione (4.5.1).
4 W è calcolata dividendo la devianza e codevianza interna per i gradi di libertà e
non per il totale delle osservazioni (20 osservazioni e 2 gruppi: 20–2=18 gradi di
libertà).
62
Previsione insolvenze
La quota totale di errata classificazione è 4/20 (3/10 nel gruppo delle
aziende fallite e 1/10 nel gruppo delle sane).
Ricaviamo ora la funzione discriminante lineare. A tale scopo
facciamo riferimento all’espressione (6.1.7) del capitolo 6 poiché i
risultati forniti dai package statistici (es. Statistica, SAS) assumono la
forma rappresentata nella Tab. 4.4.6:
Tab. 4.4.6 Funzione discriminante lineare
G1
Formula
Ratio
G0
CR
63.924
66.433
DP
171.222
176.877
W–1mj’
ROA
7.811
1.626
FD
–4.797
–5.801
Costante
–112.998
–119.874 –0.5 mjW–1mj’
da cui:
66.433 − 63.927 2.509
176.877 − 171.222 5.655
a=
=
1.626 − 7.811 − 6.185
− 5.801 − 4.797 − 1.004
k=–112.998+119.874=6.876
Pertanto, la funzione discriminante lineare è:
Z=2.509 CR + 5.655 DP–6.185 ROA–1.004 FD
con cut-off uguale a 6.876, di modo che se Z>6.876 l’unità è
dichiarata insolvente. Funzione discriminante lineare equivalente è:
(4.5.1)
Z1=Z–6.876
che ha cut-off zero. In tal caso l’azienda è dichiarata insolvente se
Z1>0. I valori del punteggio discriminante Z1 sono stati riportati nella
Tab. 4.4.5. Z1 è una misura di rischio di insolvenza, in quanto valori
elevati corrispondono ad aziende critiche.
Ulteriori analisi sulla capacità discriminante (o predittiva) del modello
possono essere condotte esaminando le caratteristiche distributive dei
Previsione insolvenze
63
valori di Z1 (o di Z) all’interno dei due gruppi e, eventualmente,
effettuando test delle ipotesi (ad esempio un’analisi della varianza per
verificare l’ipotesi di uguaglianza delle medie di gruppo di Z1 o Z).
Bisogna osservare tuttavia che, a causa della ridotta numerosità di
osservazioni, non è possibile proporre un’analisi esterna e quindi, sia
la matrice di riclassificazione sia eventuali analisi statistiche sui
punteggi discriminanti, devono limitarsi ad un controllo interno.
Se si ritiene che il modello sia in grado di classificare in modo
adeguato le aziende nei due gruppi, si passa ad interpretare il
significato della (4.5.1), rispondendo alla seguente domanda: quali
sono gli indici di bilancio più importanti ovvero maggiormente in
grado di segnalare situazioni di crisi?
Per rendere agevole la trattazione ci limiteremo all’analisi del
coefficiente di correlazione lineare fra ogni singolo ratio e il
punteggio discriminante (si tratta della correlazione interna ovvero
calcolata mediante le varianze e covarianze interne)5.
Dalla Tab. 4.4.6 possiamo dedurre quanto segue.
•
I segni dei legami espressi dai coefficienti di correlazione sono
coerenti con le attese. All’aumentare di CR, ROA e FD (segnale
di miglioramento della liquidità e redditività) diminuisce il
punteggio discriminante (miglioramento dello stato di salute).
All’aumentare (diminuire) di DP aumenta (diminuisce) Z ovvero
Z1.
•
Alto indebitamento (complessivo, sia a breve sia a lungo) e bassa
redditività appaiono gli elementi più rilevanti nel segnalare
situazioni di crisi. Infatti DP e ROA presentano correlazioni più
strette col punteggio discriminante.
L’impossibilità di condurre un’analisi esterna rende abbastanza
incerta la capacità predittiva del nostro modello. Pertanto
concludiamo qui la descrizione dello studio di caso.
5 E’ opportuno osservare che i coefficienti della (4.1.1) non sono direttamente
confrontabili in quanto risentono della differente scala in cui sono espresse le
variabili (v. medie e varianze degli indici di bilancio in Tab. 4.4.3), Inoltre, tali
coefficienti misurano l’effetto parziale di ogni singolo ratio tenuti costanti i valori
degli altri indici e, quindi, l’interpretazione è meno immediata.
Analisi delle componenti principali
5.
65
Nota metodologica.
Analisi delle componenti principali (ACP)
Introduzione
5.1 Aspetti algebrici coinvolti nell’ACP
5.2 L’ACP
5.3 La scelta del numero di componenti
5.4 Interpretazione delle componenti selezionate
5.5 ACP: matrice S o matrice R ?
5.6 Esempi numerici
Introduzione
L’analisi delle componenti principali o ACP è un metodo esplorativo
di riduzione dei dati. Esplorativo in quanto non contempla la verifica
di modelli probabilistici. Metodo di riduzione dei dati in quanto si
propone di rappresentare l’insieme delle unità descritto da un set di k
variabili osservate su n individui, mediante un numero ridotto p<k di
nuove variabili: le componenti principali. Tali componenti principali
sono combinazioni lineari delle variabili originarie, fra loro
ortogonali e aventi, per convenzione, media nulla e varianza unitaria.
La riduzione dei dati non è indolore; qualche informazione viene
comunque perduta. Tuttavia, fra tutte le possibili combinazioni lineari
che possono essere formate con quel set di n valori assunti dalle k
variabili, la componente principale è quella che ha la massima
varianza. Quindi, quale metodo di riduzione dei dati, l’ACP cerca di
limitare la perdita di informazioni riguardo al grado di variabilità dei
dati, espressione questa delle peculiarità individuali.
5.1 Aspetti algebrici coinvolti nell’ACP
L’ACP sfrutta alcune proprietà possedute dalle matrici simmetriche
definite positive. Data H una matrice simmetrica definita positiva,
questa può essere rappresentata attraverso la seguente espressione:
(5.1.1)
H=ΓΛΓ’
66
Analisi delle componenti principali
dove Λ è una matrice diagonale (kxk) con elementi (λ1,λ2,…,λk), detti
autovalori di H; Γ è una matrice (kxk) con vettori colonna (γ1,…,γk)
detti autovettori di H, fra loro ortogonali (cioè Γ’Γ=Ι, con Ι matrice
identità (kxk)). Ogni coppia j (j=1,…,k) di autovalore-autovettore (e
cioè j-esimo elemento della diagonale di Λ e j-esima colonna di Γ)
verifica la seguente equazione:
(5.1.2)
(H-λjI)γj=0
La (5.1.1) è detta anche trasformazione per similitudine (o
fattorizzazione o anche diagonalizzazione) della matrice H in quanto,
premoltiplicando la (5.1.1) per Γ’ e postmoltiplicando per Γ, si
ottiene:
(5.1.3)
Λ=Γ’Η Γ
e H e Λhanno lo stesso determinante e la stessa traccia (somma degli
elementi che stanno sulla diagonale):
(5.1.4)
traccia(H)=traccia(Λ)
Inoltre, un’importante proprietà delle matrici simmetriche definite
positive risiede nel fatto che gli autovalori sono sempre numeri reali
positivi.
5.2 L’ACP
Come in tutti i metodi statistici multivariati, il punto di partenza
dell’analisi è costituito dalla matrice dei dati X avente n righe (le
unità) e k colonne (le variabili, tutte di natura quantitativa):
(5.2.1)
X:{xij}, i=1,…,n; j=1,…,k;
Il simbolo xij rappresenta il valore della variabile j osservato
sull’unità i. Ogni riga i della matrice X, che indichiamo con xi,
contiene i valori delle k variabili osservate sull’i-iesima unità.
Costruiamo, a partire da X, la matrice X*, che contiene gli scarti dei
valori dalla corrispondente media aritmetica:
Analisi delle componenti principali
(5.2.2)
67
X*:{xij*}, i=1,…,n; j=1,…,k;
dove xij*=xij–mj e mj è la media aritmetica dei valori relativi alla
variabile i. Usando, X* ricaviamo facilmente la matrice di varianza e
covarianza S, avente dimensione kxk, che è:
(5.2.3)
S=(X*’X*)/n
Si ricorda che sulla diagonale di S si trovano le varianze delle k
variabili, per cui traccia(S) è la somma di tali varianze. Assumiamo
qui che S ammetta l’inversa. Costruiamo, infine, la matrice Z, che
contiene gli scarti standardizzati:
(5.2.4)
Z:{zij}, i=1,…,n; j=1,…,k;
dove zij=xij/sj e sj è lo scarto quadratico medio dei valori relativi alla
variabile i (ovvero è la radice quadrata dell’i-esimo elemento della
diagonale di S).
La matrice di varianza e covarianza calcolata sui dati di Z è la matrice
di correlazione R dei valori originari contenuti in X:
(5.2.5)
R=(Z’ Z)/n
Sulla diagonale principale di R si trovano k termini unitari; pertanto
traccia(R) è la somma di k valori 1, e cioè traccia(R)=k. Poiché
abbiamo assunto S non singolare, anche R ammette l’inversa.
Definiamo quindi la componente principale y come:
(5.2.6)
y=X* γ
dove γ:{γ1,...,γk} è un vettore colonna di k coefficienti da determinare.
Da notare che y è un vettore colonna di n valori con media nulla. La
(5.2.6) dice che il valore della componente yi corrispondente alla iesima unità è definito come:
(5.2.7)
yi=xi γ = Σj xij* γj
68
Analisi delle componenti principali
I coefficienti in γ sono determinati in modo da massimizzare la
varianza dei valori di y che è:
(5.2.8)
(y’y)/n= (X* γ)’(X* γ)/n=γ’(X*’X*)γ/n=γ’Sγ.
con γ’Sγ scalare.
Dalla (5.2.7) si capisce che la scala di y dipende da γ. Ciò significa
che valori arbitrariamente grandi di γ generano varianze grandi; in
questo modo non si può pervenire ad una soluzione unica. E’ quindi
necessario introdurre un vincolo sui coefficienti di γ. Il vincolo che
viene convenzionalmente usato è:
(5.2.9)
γ’γ=1.
Quindi si costruisce l’espressione F(γ,λ) da massimizzare rispetto a γ e
λ, che tiene conto del vincolo (5.2.9):
(5.2.10)
MAXγ,λ F(γ,λ)=MAXγ,λ {γ’Sγ.– λ (γ’γ–1)}
Il simbolo λ è detto moltiplicatore di Lagrange e serve a inglobare il
vincolo (5.2.9) nell’operazione di massimo.
Calcolando le derivate prime della (5.2.10) rispetto a γ e λ ed
uguagliandole a zero, si ricava il seguente sistema di k+1 equazioni1:
(5.2.11)
δ F(γ,λ)/δγ = 2Sγ–2λ γ = (S–λ Ι)γ=0
δ F(γ,λ)/δλ=γ’γ–1=0
dove I è la matrice identità di dimensione kxk e la derivata prima
rispetto a λ non è altro che l’esplicitazione del vincolo (5.2.9).
Confrontando la (5.2.11) con la (5.1.2) si deduce immediatamente che
λ è autovalore di S e γ è l’autovettore associato. Ma quale autovalore
visto che, per le proprietà delle matrici simmetriche e non singolari
(come è qui S), S ha k autovalori reali positivi 2? La risposta viene
1
Si fa notare che la (5.2.11) è una derivata rispetto ad un vettore con k componenti
e, quindi, trattasi di k equazioni.
2
Condizione per la verifica della (5.2.11) è l’annullamento del determinante della
matrice (S–λ Ι). Pertanto, il valore di λ che soddisfa alla (5.2.11) è quello che
Analisi delle componenti principali
69
ancora dalla (5.2.11) che ci consente una interpretazione di λ in chiave
statistica. Premoltiplicando la (5.2.11) per γ’ e tenendo conto del
vincolo (5.2.9), si ottiene:
γ’Sγ–λγ’ γ =γ’Sγ–λ=0
da cui:
(5.2.12)
λ =γ’Sγ
e cioè, λ è proprio la varianza che vogliamo massimizzare (v.
espressione 5.2.8). Quindi, fra tutti gli autovalori di S, sceglieremo
quello più grande.
Mediante l’operazione di fattorizzazione descritta nel paragrafo 5.1,
possiamo infine esprimere S mediante i suoi autovalori e autovettori
come S=ΓΛΓ’, dove Λ è la matrice di varianza e covarianza delle k
componenti. Infatti, dato che gli autovettori sono ortogonali fra loro,
le componenti sono ortogonali e quindi incorrelate (Λ è diagonale).
Inoltre, poiché traccia(S)=traccia(Λ), si deduce che tutte le k
componenti recuperano il totale della variabilità dei dati originali,
espressa dalla somma delle varianza delle k variabili.
Se si estraggono tutti gli autovalori e tutti gli autovettori di S, la
matrice Y:{yij}, di dimensione nxk, dei valori assunti dalle k
componenti principali è:
(5.2.13)
Y=X Γ
5.3 La scelta del numero di componenti
La riduzione dei dati interviene allorché si decide di selezionare solo
alcune componenti: ad esempio p<k. La scelta si orienterà per le p
componenti che hanno associata varianza più elevata.
I criteri per la scelta del numero p di componenti, tengono conto del
grado di efficacia della riduzione dei dati e dell’entità di informazione
mantenuta (varianza recuperata o spiegata, in totale e per ogni singola
variabile).
annulla il determinante della matrice (S–λ Ι). Se detta matrice è di dimensione kxk, il
determinante sarà un polinomio in λ di grado k.
70
Analisi delle componenti principali
Grado di efficacia della riduzione. Esso può essere espresso
semplicemente dal rapporto p/k.
Entità dell’informazione mantenuta. Essa può venire espressa
attraverso la quota di varianza totale (somma delle varianze delle
variabili originarie) spiegata da p componenti. Ipotizzando di avere
ordinato le componenti per valori decrescenti delle corrispondenti
varianze (λ1>λ2>...>λk), tale quota è data da:
(5.3.1)
p
k
j =1
j =1
∑ λ j/ ∑ λ
j
Ovviamente, aumentando p si ottiene un valore più alto della (5.3.1)
ma, nel contempo, si realizza una minore riduzione dei dati. La scelta
è di fatto piuttosto soggettiva, dipendendo anche dal contesto
applicativo. In generale potremo essere soddisfatti della riduzione dei
dati se (5.3.1) supera 0.75.
Un altro criterio di selezione è quello basato sull’autovalore medio,
secondo il quale, vengono scelte quelle componenti che hanno
associato un autovalore (cioè una varianza) superiore alla media
aritmetica dei k autovalori.
Non sempre i due criteri appena descritti conducono alle stese
decisioni.
Un altro elemento che può essere tenuto in considerazione nella scelta
delle componenti e nella valutazione dei risultati, è la quota di
varianza di ogni singola variabile che viene spiegata dalla p
componenti principali selezionate. Tale quota di varianza spiegata non
è altro che l’indice di determinazione lineare di ogni variabile
originaria rispetto alle p componenti3.
5.4 Interpretazione delle componenti selezionate
Operata la scelta del numero di componenti e, se si ritiene che la
riduzione dei dati sia soddisfacente, si può passare all’interpretazione
delle componenti. Infatti, una ACP è utile quale metodo di riduzione
dei dati, a patto che le nuove variabili individuate (le componenti,
appunto) esprimano aspetti significativi del fenomeno sotto studio.
3
Si tratta dell’indice di determinazione lineare di un modello lineare che ha come
variabile dipendente la variabile originaria i-esima e come regressori le p
componenti principali scelte.
Analisi delle componenti principali
71
Ai fini interpretativi, ci limitiamo qui a descrivere il criterio basato
sulla correlazione lineare fra variabili e componenti.
La stretta associazione lineare fra una componente e una variabile
indica che al variare dell’una varia anche l’altra: in modo concorde
(correlazione positiva) o no (correlazione negativa). Pertanto, una
componente che risulta marcatamente correlata con, ad esempio, due
delle k variabili, misura, in modo più sintetico, il fenomeno descritto
da quelle due variabili. L’interpretazione viene facilitata quando una
componente è correlata solo con alcune variabili che, a loro volta, non
sono correlate con le altre componenti.
Può accadere che alcune variabili siano fortemente correlate con una
delle k-p componenti scartate (quelle, cioè, che hanno associata una
varianza bassa) e con nessuna delle componenti scelte. Si tratta di
variabili di secondo piano: le n unità sotto studio non si differenziano
in modo particolarmente significativo rispetto a quelle stesse variabili.
Una volta interpretato il significato delle p componenti selezionate,
viene effettivamente realizzata la riduzione dei dati. Infatti possiamo
così sostituire la matrice nxk dei dati X (ovvero X*) con quella nxk
delle componenti, dove:
(5.4.1)
Y(p)=X* Γ(p)
e l’apice (p) sta a significare che sono presenti solo p colonne.
L’analisi del fenomeno potrà quindi avvenire attraverso le nuove
variabili. La sintesi dell’ACP sarà molto utile tutte le volte che si
riusciranno a selezionare 2 o 3 componenti. Infatti, in quelle
situazioni, sarà molto facile proporre semplici analisi grafiche che,
molto spesso, sono quelle più efficaci.
5.5 ACP: matrice S o matrice R ?
Abbiamo visto come l’ACP riesce a riprodurre la somma delle
varianze delle variabili originarie, attraverso le k componenti. Nelle
applicazioni empiriche abbiamo spesso a che fare con variabili
espresse in diversa unità di misura (es. litri, Kg., Lire, Euro): che
significato ha in questo caso l’espressione traccia(S) ? Un minimo di
attenzione è richiesta per capire che, così facendo, si stanno
sommando grandezze espresse in diversa unità di misura.
72
Analisi delle componenti principali
Per ovviare a questo problema, quando si ha a che fare con variabili di
natura diversa, si preferisce condurre l’ACP su R anziché su S. Questo
procedimento equivale a definire la componente principale in funzione
degli scarti standardizzati contenuti in Z:
(5.5.1)
y=Zγ.
L’ACP si traduce quindi nella derivazione degli autovalori e
autovettori di R invece che di S.
Nel complesso, usando R, alcune operazioni e interpretazioni vengono
semplificate:
• la somma delle varianze delle variabili originarie e quindi la
somma degli autovalori di R, è k;
• il criterio basato sull’autovalore medio diventa il seguente: si
selezionano le componenti che hanno associato un autovalore
superiore a 1 (infatti 1 è proprio la media degli autovalori di R);
• gli elementi dell’autovettore γ sono direttamente confrontabili in
quanto non risentono della scala o dell’unità di misura delle
variabili originarie. Il valore γj esprime la variazione della
componente dovuta ad una variazione della variabile j-esima, pari
a sj, tenuti costanti i valori delle altre variabili. Quindi, all’interno
della combinazione lineare che definisce una componente, è
possibile valutare il peso relativo rivestito da ogni variabile.
E’ bene sottolineare il fatto che, in generale, i risultati di una ACP
condotta su R sono diversi da quelli ottenuti da S e che non si può
passare dagli uni agli altri attraverso una semplice trasformazione di
scala delle componenti. L’efficacia dell’ACP quale metodo di
riduzione dei dati è diversa (si ottengono autovalori diversi) e perfino
il significato delle componenti può non coincidere.
Questo è comprensibile se si pensa al tipo di informazione che viene
utilizzata:
• traccia(R): le varianze delle k variabili sono tutte uguali a 1. In
questo caso ogni variabile presenta la medesima quota di varianza
totale, pari a 1/k;
• traccia(S): se le varianze delle k variabili originarie sono molto
diverse fra loro, ogni variabile i presenta una diversa quota di
varianza totale (rapporto fra la varianza della variabile e la
traccia(S)). Se, per esempio, una sola variabile ha una varianza
pari a oltre l’80% della somma delle varianze, l’ACP tenderà a
Analisi delle componenti principali
73
produrre una componente principale, altamente correlata con tale
variabile, e che, da sola, assorbirà un’alta quota di varianza.
Da questi brevi commenti si deduce che, operando con S in presenza
di forti differenze fra i valori delle varianze, si ottengono risultati
migliori (sia in termini di riduzione dei dati sia in termini
interpretativi) di quelli realizzabili con R.
Tuttavia, il rischio di una disparità di trattamento delle variabili
originarie, induce a chiederci se l’utilizzo di S possa generare
problemi anche in presenza di variabili della stessa natura (stessa unità
di misura) ma con varianze fortemente diversificate. In questa
circostanza, la decisione su S o R passa per il seguente quesito: la
gerarchia delle variabili, implicitamente operata dai valori della
varianza, rispecchia il grado di importanza che le variabili stesse
rivestono nel contesto analizzato? Se la risposta è sì, allora conviene
usare S, anche perché i risultati saranno, nel complesso, migliori. Se la
risposta è no allora è preferibile usare R.
Un’ultima osservazione che verrà approfondita con la presentazione di
esempi applicativi, concerne il fatto che la struttura di correlazione
esistente fra le k variabili influenza l’efficacia dell’ACP quale metodo
di riduzione dei dati (sia che operi su S sia che operi su R). Infatti, a
parità di k, in presenza di alta correlazione fra le variabili originarie,
una stessa quota di varianza spiegata tende ad essere riprodotta con un
minor numero di componenti rispetto a quanto avviene in una
situazione di bassa correlazione.
5.6 Esempi numerici
In questo paragrafo presentiamo alcuni esempi di applicazione
dell’ACP, compreso un caso numerico.
Brevemente delineiamo qui le fasi per la conduzione di una ACP:
1) scelta delle variabili e esame del loro grado di correlazione;
2) decisione in merito all’uso di R o di S;
3) estrazione delle componenti e scelta del numero, verificando
l’efficacia della riduzione dei dati;
4) interpretazione delle componenti e relativa analisi del fenomeno
sotto studio.
74
Analisi delle componenti principali
5.6.1 Esempio numerico
Si consideri la matrice dei dati X relativa alle due variabili X1 e X2, le
corrispondenti X* e Z, riportate nella Tab. 5.6.1, e le matrici S e R.
Tab. 5.6.1 Matrice dei dati (n=6; k=2)
X
X*
Unità i
x1i
x2i
x1i*
x2i*
1
2
1
-2
-0.5
2
2
1
-2
-0.5
3
3
0
-1
-1.5
4
5
2
1
0.5
5
6
2
2
0.5
6
6
3
2
1.5
Media
4.00
1.50
0.00
0.00
SQM
1.73
0.96
1.73
0.96
SQM: scarto quadratico medio
S:
3.00 1.33
1.33 0.92
R:
Z
z1i
-1,15
-1,15
-0,58
0,58
1,15
1,15
0.00
1.00
z2i
-0,52
-0,52
-1,57
0,52
0,52
1,57
0.00
1.00
1 0.8
0.8 1
Vediamo la marcata differenza fra le varianze delle due variabili (v.
diagonale della matrice S). La variabile X1, avendo una varianza più
alta, viene ad assumere un’importanza superiore a X2.
Ai fini esemplificativi, ricaviamo le componenti principali dalla
matrice di correlazione R, eseguendo i vari passaggi algebrici che, nel
caso di due sole variabili, sono abbastanza agevoli. Si noti che
traccia(R)=2.
Per prima cosa, impostiamo la condizione (5.2.11) rispetto a R:
(R–λI)γ=0
che è:
1 0.8 λ 0 1 - λ 0.8 0
−
=
=
0.8 1 0 λ 0.8 1 - λ 0
Essa è verificata da quei valori di λ che annullano il determinante di
(R–λI), dato dalla seguente espressione:
Analisi delle componenti principali
75
det(R–λI)=(1–λ2)–0.82= λ2–2λ+0.36=0
Come si vede, avendo k=2, il determinante è un’equazione di secondo
grado in λ. Le soluzioni sono:
λ1=1.8
λ2=0.2
Si verifica immediatamente che λ1+λ2=2. La componente più
importante è quella associata all’autovalore 1.8, pari al 90% (1.8/2)
della varianza totale. Possiamo quindi realizzare una riduzione dei dati
pari a ½ (da 2 variabili a 1 componente).
Andiamo a determinare il valore di γ:( γ1, γ2) associato all’autovalore
1.8. Riprendendo la (5.2.11), si ricava il seguente sistema in due
equazione e due incognite (gli elementi di γ):
(1–1.8) γ1+0.8 γ2 =0
0.8 γ1+(1–1.8) γ2 =0
ÍÎ
ÍÎ
γ1=γ2
γ1=γ2
Come si vede facilmente, le due equazioni identificano la stessa
relazione fra γ1 e γ2. Ciò significa che infinite coppie di valori γ1 e γ2
verificano le due equazioni4. Da ciò si capisce l’utilità del vincolo
γ ’γ= γ12+ γ22=1. Pertanto il sistema di equazioni che ci dà il valore γ è:
γ1=γ2
γ12+ γ22=1
da cui si ricava γ12=1/2 e quindi γ1=±2−0.5=±0.707. Da questo risultato
si capisce che il sistema di riferimento individuato dalle componenti
principali è arbitrario. Infatti, è equivalente scegliere la soluzione
negativa o quella positiva (si hanno, in corrispondenza, due
rappresentazioni speculari).
Selezionando la soluzione positiva si ottiene il vettore dei coefficienti
γ:(0.707, 0.707). La formula per il calcolo della componente
principale associata all’autovalore 1.8 è quindi, per ogni unità i-esima:
4
E’ questo un altro modo di vedere che, senza un vincolo sulle componenti di γ, non
si avrebbe una soluzione unica.
76
Analisi delle componenti principali
yi= γ1 z1i + γ2 z2i = 0.707 z1i + 0.707 z2i
I valori così calcolati su tutte le unità hanno media zero e varianza 1.8.
Spesso (e i package statistici così fanno) i coefficienti vengono scalati
in modo da ottenere componenti principali con media zero e varianza
unitaria. Nel nostro caso si tratterebbe di dividere il vettore γ per lo
scarto quadratico medio della componente principale (che, nel nostro
caso, è uguale alla radice quadrata di 1.8). Operata questa
trasformazione, il valore della componente principale standardizzata,
per l’unità i-esima, è:
[s]yi=
0.527 z1i + 0.527 z2i
dove 0.527=0.707/(1.8)0.5. La Tab 5.6.2 mostra i valori delle due
componenti principali, che si ottengono per le 6 unità dell’esempio
numerico.
Resta da interpretare il significato della componente scelta. I due
coefficienti di correlazione lineare fra i valori di questa e delle due
variabili sono in questo caso uguali fra loro e pari a 0.95 (è questo,
ovviamente, un caso molto particolare). Quindi la componente
principale sintetizza in modo concorde (a valori elevati delle variabili
corrispondono valori elevati delle due variabili e viceversa) ambedue
le variabili.
Tab. 5.6.2 Valori della componente principale
Componente
Unità
yi
[s]yi
1
-1.19
-0.88
2
-1.19
-0.88
3
-1.52
-1.13
4
0.78
0.59
5
1.19
0.88
6
1.93
1.44
Media
0.00
0.00
Varianza
1.80
1.00
5.6.2 Esempio numerico: confronto fra uso di S e di R
Quale sarebbe stato il risultato se si fosse usata la matrice di
covarianza S ?
Analisi delle componenti principali
77
Ci limitiamo a dire che i due autovalori sono pari a 3.65 e 0.27 (da
notare che 3.65+0.27=3.92, somma delle varianze delle due variabili).
Pertanto la prima componente principale assorbe circa il 93%
(3.65/3.92) della varianza totale. Essa risulta, inoltre, più correlata con
la prima variabile (coefficiente di correlazione pari a 0.99) che con la
seconda (coefficiente di correlazione pari a 0.87).
Da questi risultati si deduce il maggior ruolo rivestito dalla prima
variabile che favorisce anche l’efficacia della riduzione dei dati: con
S, una sola componente spiega il 93% della varianza mentre con R ne
spiega il 90%.
5.6.3 Esempio numerico: correlazione debole
Si consideri la seguente matrice di correlazione R:
R:
1 0.2
0.2 1
I due autovalori associati sono λ1=1.2, λ2=0.8 ai quali corrisponde,
rispettivamente, il 60% (1.2/2) e il 40% (0.8/2) della varianza totale.
La quota di varianza spiegata dalla prima componente è inferiore
rispetto a quanto ottenuto nell’esempio 5.6.1, in presenza di una forte
correlazione fra le due variabili.
Analisi discriminante
6.
79
Nota metodologica. Analisi discriminante (AD)
Introduzione
6.1 Analisi discriminante e problemi classificatori
6.1.1 Teoria decisionale
6.1.2 La funzione discriminante
6.1.3 Funzione discriminante e AD normale
6.1.4 Funzione discriminante e AD logistica
6.2 Stima della funzione discriminante (AD normale)
6.3 Verifica della capacità classificatoria della funzione discriminante
6.4 Esempio numerico
Introduzione
L'analisi statistica multivariata di dati di bilancio è frequentemente
usata per l'individuazione di imprese a rischio di insolvenza. Dal punto
di vista puramente teorico l'insieme dei metodi impiegati in questo
ambito rientrano in quelle che potremo definire tecniche classificatorie.
Esse si propongono di assegnare un oggetto (nella fattispecie
un'impresa) ad uno dei possibili gruppi (spesso si tratta di due soli
gruppi: imprese sane ed imprese insolventi) sulla base di una serie di
grandezze (variabili) osservate sull'oggetto stesso (es. indici di
bilancio).
In particolare, nell'ambito della diagnosi precoce del rischio di
insolvenza aziendale, la tecnica dell'analisi discriminante (AD) è stata
quella più usata, tanto che essa ha travalicato da tempo l'ambito
accademico per trasformarsi in un vero e proprio strumento operativo.
Il termine discriminante fa riferimento al processo di derivazione di
una regola discriminatoria da un insieme di unità delle quali è nota
l'appartenenza ai gruppi e sulle quali unità sono state osservate un certo
numero di variabili. Gli obiettivi a cui mira la derivazione di questa
regola discriminante sono i seguenti.
1) Descrittivi ed esplicativi: tale regola evidenzia le differenze fra i
gruppi di imprese, segnalando le variabili che maggiormente sono
responsabili di tale differenziazione. L’analisi si limita, pertanto, a
spiegare ed interpretare le eventuali differenze emerse fra gruppi di
unità.
80
Analisi discriminante
2) Predittivi: tale regola si pone come vera e propria regola
classificatoria da applicare ogniqualvolta sia necessario classificare
una unità (la cui appartenenza ai gruppi è sconosciuta) in uno dei
possibili gruppi. E’ questo lo scopo perseguito nell’utilizzo della
AD per la costruzione di modelli per la previsione delle insolvenze
aziendali.
In questo scritto faremo riferimento principalmente all’obiettivo 2).
Nella descrizione dei metodi di AD, proponiamo alcune regole
classificatorie, che richiedono la specificazione di un modello
probabilistico da stimare e verificare su dati empirici. Pertanto, l’AD
viene vista essenzialmente come approccio di natura confermativa.
I modelli proposti caratterizzano due tipi di AD: quella che
chiameremo normale, perché basata sulla distribuzione normale, e
quella logistica (perché basata sulla distribuzione logistica).
Come vedremo in queste note, l’AD normale e l’AD logistica sono
caratterizzate da due ottiche di analisi diverse. Prima di approfondire
queste tematiche, è necessario introdurre alcune regole classificatorie
sulle quali verrà incardinata l’analisi statistica.
6.1 Analisi discriminante e problemi classificatori
Introduciamo in questo capitolo le basi teoriche sottostanti l'analisi
discriminante, considerando la questione classificatoria come un
problema decisionale. Inoltre verificheremo le regole decisionali
esplicitate al caso di distribuzione normale, descrivendo l'analisi
discriminante 'normale' (lineare). Infine, confronteremo la AD normale
con quella logistica.
6.1.1 Teoria decisionale
Si consideri una popolazione composta da 2 sottopopolazioni o gruppi
(disgiunti ed esaustivi) di unità, indicati con G1 e G0 (ad esempio G1:
gruppo delle aziende insolventi o fallite e G0: gruppo delle aziende
solventi o sane). Sia P(Gj)=pj la probabilità che una generica unità
provenga dal gruppo Gj (j=0,1). pj è una probabilità, che non dipende
dalle caratteristiche della singola unità e che, pertanto, possiamo
considerare come una probabilità a priori. Il valore di pj riproduce la
proporzione del gruppo j-esimo all'interno della popolazione.
Indicando, quindi, con N la numerosità della popolazione, con Nj il
Analisi discriminante
81
numero di unità del gruppo j, si ha: pj=Nj/N. Ovviamente, poiché i due
gruppi sono esaustivi e disgiunti, p1+p0=1.
Supponiamo di non poter osservare alcuna caratteristica specifica sulle
unità della popolazione. In tal caso, estraendo una unità a caso, a quale
gruppo converrà assegnarla ? E in base a quale criterio di convenienza?
In questa circostanza, la regola decisionale migliore per classificare le
unità fra i due gruppi, (migliore nel senso che minimizza la probabilità
a priori di errata classificazione), è la seguente:
(6.1.1)
se p1 > p0 si assegna l’unità a G1
altrimenti a G0.
Dal punto di vista applicativo questa soluzione è abbastanza banale in
quanto consiste nell’assegnare tutte le unità al gruppo la cui probabilità
a priori è più elevata. In tal caso, se p1>p0, p0 sarà la proporzione di
unità della popolazione classificate in modo errato.
La (6.1.1) è, nella pratica, poco interessante perché frequentemente è
possibile osservare alcune informazioni sull’unità estratta, che ci
possono aiutare nell’effettuare la classificazione. Tali informazioni
vengono qui rappresentate come un vettore (riga) x di q variabili (dati
di bilancio relativi ad un'azienda).
Ebbene, supponiamo che i q valori x siano determinazioni di una
variabile casuale (v.c.) multivariata X avente funzione di probabilità
(congiunta) all'interno di ogni gruppo P(x|Gj), j=0,1 (se X è continua
si tratterà della funzione di densità di probabilità). Poniamo, inoltre, di
estrarre l’unità i e di osservare il vettore di q valori xi. In tal caso
possiamo usare la regola classificatoria detta della verosimiglianza
massima:
(6.1.2)
se P(xi |G1) >P(xi |G0) si assegna l’unità i a G1
altrimenti a G0 .
Infatti P(xi |Gj) è la verosimiglianza di xi nel gruppo j (j=0,1).
L'informazione contenuta in xi, può essere sfruttata per arricchire la
nostra conoscenza sull'appartenenza dell'unità ad uno dei due gruppi.
Infatti, mediante il teorema di Bayes, possiamo ricavare la cosiddetta
probabilità a posteriori di appartenenza dell’unità i al gruppo j:
82
Analisi discriminante
P(Gj|xi)=P(xi|Gj) pj/P(xi)
j=0,1
dove
P(x) = P(x|G1 ) p1 + P(x|G0) p0
è la funzione marginale di probabilità della X (se X è continua si
tratterà della funzione di densità marginale). Ovviamente, P(x|Gj) è la
funzione di probabilità condizionata al gruppo j.
Usando l’espressione della probabilità a posteriori, possiamo applicare
la regola decisionale che minimizza la probabilità a posteriori di errata
classificazione e cioè:
(6.1.3) se P(G1 |xi )>P(G0 |xi ) si assegna l’unità i a G1
altrimenti a G0
Tale regola è detta anche della massima probabilità a posteriori.
Poiché P(G1|xi) e P(G0|xi) hanno il medesimo denominatore (cioè P(xi),
che è positiva), la (6.1.3) può essere riscritta come:
(6.1.4)
se P(xi |G1)/P(xi |G0) > p0/p1 si assegna l’unità i a G1
altrimenti a G0
Da notare che, nel caso speciale in cui p1=p0, la (6.1.3) coincide col
criterio della verosimiglianza massima.
6.1.2 La funzione discriminante
E’ interessante notare che le regole decisionali della verosimiglianza
massima e della massima probabilità a posteriori, operano un confronto
fra una funzione di xi e una costante. Ad esempio, ponendo
(6.1.5)
h(xi)= P(xi |G1)/P(xi |G0)
k= p0/p1
la (6.1.4) può essere riscritta come segue:
se h(xi)>k si assegna l’unità i al gruppo G1
altrimenti a G0.
Analisi discriminante
83
La funzione h(xi) è detta funzione discriminante e il punto k è detto
punto di cut-off. E' evidente che qualunque funzione che deriva da
una trasformazione monotona della h(xi) è una funzione
discriminante. Ponendo ad esempio g(xi)=h(xi)–k si perviene alla
seguente regola decisionale equivalente alla (6.1.5):
se g(xi)>0 si assegna l’unità i a G1
altrimenti a G0.
Ancora, una regola equivalente alla (6.1.5) è la seguente:
se log(h(xi))>log(k)
altrimenti a G0.
si assegna l’unità i al gruppo G1
dove, ovviamente, h(xi )>0 e k>0.
Riguardo al concetto di funzione discriminante, è importante osservare
che h( ) (e, di conseguenza anche le sue trasformazioni sopra
esemplificate) ha come argomento un vettore ma dà come risultato uno
scalare, sintetizzando quindi l'informazione multivariata fornita dal
vettore xi in una sorta di punteggio (discriminant score) individuale
dell'unità i. Infatti h(xi) della (6.1.5) è il rapporto fra due grandezze
scalari.
Nella pratica accade che la forma della funzione discriminante non è
completamente nota. Pertanto, si possono prospettare tre possibili
approcci parametrici alternativi.
1) Specificazione e stima di una forma parametrica per la P(xi|Gj). In
questo caso l’impiego del criterio della verosimiglianza massima è
immediato. Per quello della massima probabilità a posteriori si
tratterà di derivare P(Gj|xi) usando le probabilità a priori.
2) Specificazione e stima direttamente della P(Gj |xi). In questo caso
l’impiego del criterio della massima probabilità a posteriori è
immediato. Per quello della verosimiglianza massima sarà
necessario ricavare P(xi|Gj) usando le probabilità a priori.
3) Specificazione e stima di una forma parametrica che rappresenta
direttamente la h(xi), eventualmente anche senza particolari
assunzioni sulla distribuzione della X. Questo modo di procedere
può avere dei vantaggi nella misura in cui possiamo scegliere
84
Analisi discriminante
forme convenienti dal punto di vista computazionale come ad
esempio una h(xi) che sia combinazione lineare delle componenti
del vettore xi. In linea generale questo approccio non richiede
necessariamente la specificazione di un modello probabilistico.
Nei paragrafi seguenti tratteremo delle impostazioni 1) e 2).
6.1.3 Funzione discriminante e AD normale
Secondo questo approccio, condizionatamente ad ogni gruppo viene
specificata la funzione di probabilità congiunta delle q variabili.
Supponendo di avere 2 gruppi G1 e G0, si ipotizza che l'insieme dei q
valori del vettore (riga) xi osservato sull'individuo i-esimo siano le
determinazioni di una variabile casuale (v.c.) normale multivariata X
tale che:
X |G 1 ~ MN (µ1, Σ)
X |G 0 ~ MN (µ0, Σ)
dove MN sta per multinormale e µj e Σ sono, rispettivamente, il
vettore (riga) delle medie e la matrice di varianza e covarianza di X nel
gruppo j-esimo (i=0,1). Ci limitiamo al caso in cui i due gruppi
abbiano la stessa matrice di varianza e covarianza Σ. Allora la
verosimiglianza dell’unità i nel gruppo j è:
|Σ|-1/2 (2π)q/2 exp {–½(xi–µj)Σ–1(xi–µj)’}
dove il segno |Σ| indica l’operazione di determinante e q, si ricorda, è il
numero delle variabili.
L'applicazione del criterio della verosimiglianza massima, una volta
operata la trasformazione logaritmica, ci conduce alla regola di
classificazione seguente:
(6.1.6) se (xi–µ0)Σ–1(xi–µ0)’> (xi–µ1)Σ–1(xi–µ1)’ si assegna i a G1
altrimenti a G0.
L’espressione (xi–µj)Σ–1(xi–µj)’ è una misura di distanza fra il punto
individuato da xi nello spazio q-dimensionale e il punto individuato da
µj (detto centroide del gruppo j). Essa è il quadrato della cosiddetta
Analisi discriminante
85
distanza di Mahalanobis o distanza generalizzata. Si definisce distanza
generalizzata in quanto, se Σ è la matrice identità a q dimensioni, la
distanza di Mahalanobis coincide con la distanza euclidea nello spazio
(euclideo) a q dimensioni.
Quindi, nell’ipotesi di distribuzione multinormale con stessa matrice di
covarianza interna ai gruppi, la regola della verosimiglianza massima
assegna l’unità i-esima al gruppo col centroide meno distante da xi, in
termini di distanza di Mahalanobis.
Tuttavia, l’espressione (6.1.6) si presta ad ulteriori interpretazioni.
Infatti, dopo alcuni passaggi algebrici, si ottiene:
(6.1.7) se xi (Σ–1µ1’–Σ–1µ0’)>0.5(µ1Σ–1µ1’–µ0Σ–1µ0’) assegna i a G1
da cui, ponendo a=Σ–1(µ1–µ0)’ e k=–0.5(µ0Σ–1µ0’– µ1Σ–1µ1’), si ricava
la regola classificatoria basata su una funzione discriminante linere:
se xia>k si assegna l’unità i al gruppo G1
altrimenti a G0.
Funzione discriminante equivalente e relativa decisione è:
(6.1.8)
se xia–k>0 si assegna l’unità i al gruppo G1
altrimenti a G0.
Ora, si vede facilmente che xia è una trasformazione lineare di in xi e
cioè, è una funzione discriminante lineare (infatti, a è un vettore
colonna di q elementi). Il valore assunto da detta funzione (detto
discriminant score) è naturalmente uno scalare.
L’applicazione del criterio della massima probabilità posteriori
conduce ad un diverso punto di cut-off, che è funzione anche delle
probabilità a priori:
(6.1.9)
se xia–k>log(p0/p1) si assegna l’unità i al gruppo G1
altrimenti a G0.
Anche l’interpretazione della (6.1.9) può essere fatta anche in funzione
della distanza di Mahalanobis.
86
Analisi discriminante
6.1.4 Funzione discriminante e AD logistica
Secondo questa impostazione, si ipotizza che la probabilità di
appartenenza al gruppo Gj per una unità i, dipenda da alcune sue
caratteristiche (vettore xi).
Operativamente, si tratta di specificare P(G1|xi) in funzione di xi
medesimo mediante una opportuna forma funzionale del tipo:
P(G1|xi)=Γ(xi)
tale che 0<Γ(xi)<1.
La specificazione di Γ(xi), che conduce alla discriminante logistica è
la seguente:
P(G1|xi)=Γ(xi)=exp(β0+xiβ)/[1+ exp(β0+ xiβ)]
dove β0 è l’intercetta (scalare) e β è un vettore (colonna) di
coefficienti. L’espressione assegnata a Γ(xi) è la funzione di
ripartizione di una variabile casuale logistica standard (avente, cioè,
media zero e varianza π2/3) calcolata nel punto (β0+xiβ). Ciò significa
che, la probabilità che l’unità con vettore xi appartenga al gruppo G1
è uguale alla probabilità che una variabile casuale logistica standard
Z, assuma valori minori o uguali a (β0+xiβ) e cioè P(Z≤β0+xiβ).
Con questa specificazione, si ha che:
P(G1|xi)/ P(G0|xi)=Γ(xi)/[1–Γ(xi)]=exp(β0+xiβ)
da cui è immediata l’applicazione del criterio della massima
probabilità a posteriori che ci dà la seguente regola classificatoria:
(6.1.10)
se
exp(β0+xiβ)>1
altrimenti a G0
si assegna i a G1
da cui, operando la trasformazione logaritmica, si ricava la regola
equivalente:
(6.1.11)
se
xiβ+β0 >0 si assegna i a G1
altrimenti a G0
Analisi discriminante
87
Anche in questo caso si ricava una funzione discriminante lineare che
viene confrontata con il punto di cut-off uguale a zero.
Per l’applicazione del criterio della verosimiglianza massima occorre
dividere ciascuna probabilità a posteriori per la corrispondente
probabilità a priori. Ciò ci porta alla seguente regola che si differenzia
dalla (6.1.11) per un diverso punto di cut-off:
(6.1.12)
se xiβ+β0 >log(p1/p0) si assegna i a G1
altrimenti a G0
6.2 Stima della funzione discriminante (AD normale)
La Tab. 6.2.1 riassume le funzioni discriminanti e i punti di cut-off
ricavati in corrispondenza dei due approcci e delle due regole
classificatorie qui viste.
In pratica, tuttavia, accade che i parametri coinvolti nelle regole
classificatorie (e cioè: le medie e la matrice di varianza e covarianza
comune ai due gruppi per l’AD normale, β e β0 per l’AD logistica)
non siano noti. E’ necessario pertanto stimare i parametri sulla base di
dati campionari.
Tab. 6.2.1 Funzioni discriminanti lineari per AD normale e AD logistica
FUNZIONE
PUNTO DI
CRITERIO
MODELLO
CLASSIFICATORIO
DISCRIMINANTE
CUT-OFF
Verosim. max.
(6.1.8)
0
Multinormale Σ0= Σ1
(approccio 1)
Max prob. posteriori
(6.1.9)
log(p0/p1)
Verosim. max.
(6.1.12)
log(p1/p0)
Logistico
(approccio 2)
0
Max prob. posteriori
(6.1.11)
Nella conduzione di un’analisi discriminante, è necessario affrontare le
seguenti fasi:
1) stima dei parametri della funzione discriminante;
2) verifica della capacità predittiva della funzione discriminante così
stimata. A questo proposito occorre dire che le funzioni stimate non
garantiscono sempre risultati soddisfacenti. In particolare, le
proprietà ‘ottimali’ delle regole decisionali (come ad esempio la
88
Analisi discriminante
minimizzazione della probabilità di errata classificazione) sono
garantite dai veri modelli probabilistici e cioè dalle vere forme
funzionali e dai veri valori dei parametri. Per questo motivo è
necessario, una volta stimata la funzione discriminante secondo
uno degli approcci prima delineati, procedere alla verifica della sua
capacità classificatoria.
In merito alla stima della funzione discriminante, consideriamo il caso
più frequente, che consiste nella stima da due campioni, ciascuno
estratto da una delle due sottopopolazioni: gruppo G0 e gruppo G1.
In queste note descriviamo la procedura di stima per una AD normale
nell’ipotesi di uguali matrici di covarianza interne ai gruppi. In tal caso
le stime dei parametri sono ottenute come:
1) stima dei vettori delle medie µ0 e µ1: mediante le medie, che
indichiamo con m0 e m1, calcolate all’interno dei due campioni;
2) stima della matrice di covarianza comune Σ. La stima di Σ è la
matrice di covarianza interna (within o pooled) W, che è la media
delle due matrici di covarianza calcolate separatamente sui dati
campionari relativi a ciascun gruppo. L’elemento generico shl di W
è calcolato quindi come:
shl=(n1 s1,hl+ n0 s0,hl)/(n1+n0)
dove sj,hl è l’elemento (h,l) della matrice di varianza e covarianza
calcolata sul campione del gruppo j e nj è la numerosità del gruppo Gj
nel campione (j=0,1).
Riassumendo quanto detto fin qui, la validità di una AD normale
(lineare) dipende dalle seguenti ipotesi:
1. P(x|G0) e P(x|G1) sono densità normali multivariate;
2. le matrici di varianze e covarianza dei gruppi sono uguali
(Σ0=Σ1=Σ);
3. le medie µ0 e µ1 e la matrice di varianza e covarianza Σ sono note.
Abbiamo visto che, se la 3 non è verificata, si procede ad una stima dei
parametri distributivi. Se l'assunzione 2 è violata si ottiene una
funzione discriminante quadratica in x, anziché lineare. Il punto 1,
Analisi discriminante
89
inoltre, è difficilmente sostenibile se abbiamo variabili con
distribuzione molto diversa dalla normale.
Se si ritiene valida l’ipotesi di funzione discriminante lineare, la AD
logistica si propone validamente come alternativa alla AD normale in
quanto non richiede l’assunto 1. Pertanto, in tal caso, l’AD logistica
appare più corretta ai fini della costruzione di modelli per la previsione
delle insolvenze poiché gli indici di bilancio che non hanno
generalmente distribuzioni di tipo normale.
L’AD lineare normale mantiene tuttavia una sua validità se viene
interpretata in senso geometrico attraverso la misura di distanza
generalizzata o distanza di Mahalanobis.
6.3 Verifica della capacità classificatoria della funzione
discriminante
La valutazione della capacità classificatoria di un modello di AD, a
fini predittivi (es. previsione delle insolvenze aziendali), consiste
nella risposta alla seguente domanda: quanto è accurata la regola
classificatoria, stimata su un determinato campione, per classificare
altri (ovvero futuri) campioni, che devono però ritenersi estratti dalla
medesima popolazione del primo (si tratta di verificare la validità del
modello stimato nel classificare nuove unità)?
I principali procedimenti impiegati per la valutazione della capacità
classificatoria di una funzione discriminante si distinguono in analisi
interna e analisi esterna.
Analisi interna: la capacità classificatoria viene valutata
riclassificando le medesime osservazioni usate per la stima della
funzione discriminante. Supponendo di avere stimato una funzione
discriminante da un campione di n unità, n1 delle quali estratte dal
gruppo G1 e n0 estratte dal gruppo G0, si tratta, in pratica, di applicare
uno dei criteri classificatori delineati nella Tab. 6.1.1 sulle stesse n
unità impiegate per la stima, costruendo la seguente matrice di
riclassificazione.
Tab. 6.2.1 Matrice di riclassificazione
Gruppi
Gruppi assegnati
veri
0
1
0
n00
n01
Totale
n0
90
Analisi discriminante
1
n10
n11
n1
Dalla tabella si possono ricavare le seguenti indicazioni:
– proporzione di unità correttamente riclassificate (n00+n11)/n;
– proporzione di unità del gruppo 0 correttamente riclassificate
n00/n0
– proporzione di unità del gruppo 1 correttamente riclassificate n11/n1
Se il gruppo 1 rappresenta il nostro evento di interesse, ad es.
fallimento, allora n01 è il numero dei cosiddetti falsi positivi e n10 è
il numero dei falsi negativi.
Analisi esterna: la capacità classificatoria viene valutata
classificando nuove unità ovvero osservazioni che non sono state
usate per la stima della funzione discriminante. Si tratta, in pratica,
di costruire un tabella analoga alla 6.2.1 per nuove unità, delle quali è
noto il gruppo di appartenenza ma che non hanno partecipato alla
stima della funzione discriminante.
Un modo per condurre l’analisi esterna è il seguente. Occorre
suddividere il campione di osservazioni in due sottocampioni: uno
(training sample) viene usato per la stima della funzione discriminate
e l'altro (test sample) per la validazione della regola classificatoria. I
principali problemi connessi con questo procedimento riguardano la
necessità di disporre di un campione di dimensioni adeguate.
Si può subito osservare che, ai fini della valutazione della capacità
predittiva, è preferibile agire mediante un’analisi esterna in quanto
quella interna tende, in generale, a fornire risultati più ottimistici. Se
lo scopo della AD fosse di tipo descrittivo, allora sarebbe sufficiente
la sola conduzione di un’analisi interna.
6.4 Esempio numerico
In questo paragrafo vedremo un esempio di AD normale, nell’ipotesi di
stessa matrice di varianza e covarianza interna ai gruppi. Si suppone
che la popolazione sia composta da due gruppi della stessa numerosità
(di conseguenza p1=p0=0.5), da ognuno dei quali sono state estratte 10
unità e sono state osservate due variabili: X1 e X2.
La Tab. 6.4.1 riporta i dati del campione.
Analisi discriminante
Tab. 6.4.1 Dati dell’esempio numerico di AD normale (lineare)
Gruppo Unità X1
X2
Medie
Devianze
X1
X2
X1
X2
0
1
2
1
0
2
2
1
0
3
3
0
4.00
1.5
18
5.5
0
4
5
2
0
5
6
2
0
6
6
3
0
7
3
2
0
8
5
1
0
9
7
1
0
10
4
0
1
11
6
3
1
12
7
3
1
13
7
2
8.17
3.67
14.8
7.3
1
14
9
4
1
15
10
5
1
16
10
5
1
17
7
4
1
18
9
5
1
19
10
6
1
20
10
4
91
Funzione
discriminante
3.05-9.3
3.05-9.3
4.68-9.3
7.66
9.21
9.15
4.54
7.73
10.84
6.24
9.15
10.71
10.78
13.76
15.25
15.25
10.64
13.69
15.18
15.32
Volendo proporre una AD avente fini predittivi, decidiamo di lasciare
8 unità (4 per ogni gruppo) per la verifica della capacità classificatoria
della funzione discriminante stimata. Tali osservazioni sono
contrassegnate dal carattere corsivo-grassetto.
Poiché, nel nostro caso, le proporzioni dei due gruppi sono uguali, il
criterio della verosimiglianza massima coincide con quello della
massima probabilità a posteriori. Pertanto il criterio classificatorio da
usare è dato dalla funzione discriminante (6.1.8) con cut-off uguale a k.
Tali grandezze sono funzioni delle medie, delle varianze e delle
covarianze delle variabili, che non sono note e devono quindi essere
stimate.
La Tab 6.4.1 riporta i valori delle medie interne ai gruppi. Si tratta
delle stime dei centroidi dei gruppi:
m0 = (4 1.5)
m1 = (8.17 3.67)
92
Analisi discriminante
In base ai dati riportati in tabella, le stime della varianza interna di X1
e di X2 sono:
s12=(18+14.8)/12=2.74
s22=(5.5+7.3)/12=1.07
Infine, poiché le codevianze fra X1 e X2 interne ai gruppi 0 e 1 sono
rispettivamente 8 e 9.3, la covarianza interna fra le due variabili è:
w12= (8+9.3)/12=1.44
Pertanto la matrice di varianza e covarianza pooled (cioè la stima di Σ)
è:
W: 2.74 1.44
1.44 1.07
la cui matrice inversa è inoltre:
W–1:
1.274 –1.678
–1.678 3.193
Si ricorda che abbiamo utilizzato il simbolo W perché si tratta della
matrice di varianza e covarianza interna o within.
Da questi dati è possibile ricavare il vettore a e k::
a= W–1(m1–m0)= (1.559 –0.068)
k=(m1S-1m’1 – m0S-1m’0 )/2 = (25.6–7)/2 = 18.6/2=9.3
La regola classificatoria per una generica unità sulla quale sono
osservate le due variabili X1 e X2 è la seguente:
se 1.559 X1 – 0.068 X2 – 9.3>0 l’unità è assegnata al gruppo 1
altrimenti al gruppo 0
Tale regola è stata applicata sui dati della Tab. 6.5.1. La colonna
‘Funzione discriminante’ riporta i valori ottenuti dall’espressione:
yi= 1.559X1–0.068X2–9.3
Analisi discriminante
93
su ogni unità. Il valore yi viene detto discriminant score.
Gli errori di classificazione sono contrassegnati dai valori sottolineati.
Vediamo che le unità 9 e 11 verrebbero classificate in modo sbagliato.
L’impiego della regola classificatoria stimata a fini predittivi può
essere brevemente qui descritto.
Supponiamo di voler classificare una nuova unità della quale non
conosciamo il gruppo di appartenenza e sulla quale abbiamo
osservato i valori X1=2 e X2=2. Ebbene, la funzione discriminante
stimata ci fornisce in corrispondenza lo score:
y= 1.559 2 – 0.068 2 –9.3<0
Poiché y<0, classificheremo l’unità nel gruppo 0.
Bibliografia
95
Bibliografia
Altman E.I: (1968), Financial Ratios, Discriminant Analysis and the
Prediction of Corporate Bankruptcy, Journal of Finance, n.23.
Altman E.I. (1983), Corporate Financial Distress. A complete Guide
to Predicting, Avoiding and Dealing with Bankruptcy, J.Wiley,
N.Y.
Altman E.I., G.Marco, F. Varetto (1994), Corporate Distress
Diagnosis: Comparisons Using Linear Discriminant Analysis
and Neural Networks (the Italian experience), Journal of
Banking and Finance, n.18.
Appettiti S. (1985), L’analisi discriminante e la valutazione della
fragilità finanziaria delle imprese, Contributi all’analisi
economica della Banca d’Italia, n.3.
Banca d’Italia (1995), La Centrale dei Rischi, Collane tematiche
istituzionali, Roma.
Barnes P: (1987), ‘The Analysis and Use of Financial Ratios: a
Review Article’, Journal of Business Finance and Accounting,
n. 4, 449-461.
Berry R.H., S.Nix (1991), ‘Regression v. Ratio in the Cross-Section
Analysis of Financial Statements’, Accounting and Business
Research, n.82, 107-117.
Brealy R., S. Myers (1988), Principles of Corporate Finance, 3rd ed.,
McGraw-Hill.
Cannari L., L.F.Signorini (1995), L’analisi discriminante per la
previsione delle crisi delle micro-banche, Temi di discussione,
n.258, Banca d’Italia, Roma.
Cannari L., G. Pellegrini, P.Sestito (1996), L’utilizzo di microdati
d’impresa per l’analisi economica: alcune metodologie alla luce
delle esperienze della Bamca d’Italia’, Temi di discussione,
Banca d’Italia, n.286.
Centrale dei Bilanci (1995), Un’applicazione delle reti neurali alla
diagnosi delle insolvenze, Bancaria,n.4.
Ecchia S. (1996), Il rischio di credito. Metodologie avanzate di
previsione delle insolvenze, Giappichelli ed., Torino.
Ezzamel M., C. Mar-Molinero (1990), ‘The Distributional Properties
of Financial Ratios in UK Manufacturing Companies’, Journal of
Business Finance and Accounting, n. 1, 1-29.
80
Analisi discriminante
Forestieri G. (1986), La previsione delle insolvenze aziendali’,
Giuffrè, Milano.
Fabbris L. (1983), Analisi esplorativa dei dati multidimensionali,
Cleup, Padova.
Foster G. (1986), Financial Statement Analysis, Englewood Cliffs.
Ganugi P., G. Gozzi, M. Riani (1997), ‘Il monitoraggio delle imprese
tessili nella provincia di Prato nell’ambito dell’Osservatorio
Bilanci’, Il sistema Prato: analisi e previsioni, Quaderni SIEL,
Provincia di Prato, 9-92.
Guatri L. (1986), Crisi e risanamento delle imprese, Giuffrè, Milano.
Huberty C. (1994), Applied Discriminant Analysis, Wiley.
Lev B., S.Sunder (1979), ‘Methodological Issues in the Use of
Financial Ratios’, Journal of Accounting and Economics, n. 3,
187-210.
Mainly B. F. J. (1986), Multivariate statistical methods: a primer,
Chapman and Hall, London.
Luerti A. (1992), La previsione dello stato di insolvenza delle
imprese. Il modello AL/93 di Credit Scoring elaborato in base
alla IV Direttiva CEE, EtasLibri.
McDonald B., M.H.Morris (1984), ‘The Statistical Validity of the
Ratio Method in Financial Analysis: an Empirical
Examination’, Journal of Business Finance and Accounting, n.
11, 89-97.
Maddala G.S.(1983), Limited Dependent and Qualitative Variables in
Econometrics, Cambridge University Press.
Previdi M. (1995), Analisi di bilancio: valutazioni, rating e
simulazioni, IPSOA, Milano.
Rosenberg E., A.Gleit (1994), Quantitative Methods in Credit
Management: a Survey, Journal of Operations Research, n.4.
Rossi C. (1988), Indicatori di bilancio, modelli di classificazione e
previsione delle insolvenze aziendali, Giuffrè, Milano.
Rossi C. (1992), La valutazione delle condizioni di solvibilità delle
imprese. Un modello basato sull’analisi discriminatoria’,
Cacucci editore, Bari.
Salmi T., K. Martikainen (1996), ‘A Review of Financial Ratio
Analysis’, The Finnish Journal of Business Economics, n.4,
426-448.
Bibliografia
95
Salmi T., I. Virtanen, P. Yli-Olli (1990), ‘On the Classification of
Financial Ratios’, Acta Wasaensia, n. 25, University of Vaasa,
Finland.
Teodori C. (1989), Modelli di previsione nell’analisi economicoaziendale, Giappichelli.
Viganò L. (1993), Un modello per la valutazione del rischio
creditizio, Il Risparmio, n.4.
Vitali O.
Siti Internet di interesse
http://inforcamere.padova.ccr.it
(Home page italiana delle piccole e medie imprese)
http://www.sands-trustee.com
(modello per la previsione delle insolvenze sviluppato presso la
Simon Fraser University, British Columbia)
http://ecn01.cineca.it
(siti e links di interesse economico a cura del Cineca)
http://sogig.ac.uk/subjects
(links con vari siti di interesse economico; ricerca per soggetto)
http://www.lincoln.ac.nz/acul/aaanz/papers
(pubblicazioni di contabilità e finanza a cura dell’Accounting
Association of Australia and New Zealand)
http://www.bus.olemiss.edu
(pubblicazioni, dati, modelli inerenti alla previsione delle insolvenze
aziendali)