Problema 1 Il piastrellista (Lab. Curiel)

MATh.en.JEANS
TASSELLATURA DEL PIANO
Liceo Scientifico Statale “E. Curiel”
Caterina Alessi, Eleonora Filira, Matteo Forin, Lorenzo Gamba, Mircea Muntean,
Stefano Pietrogrande, Emanuele Quaglio, Marco Venuti, Federico Vettore.
Prof. Giorgio Ciociano, Prof. Alberto Zanardo, Prof. Riccardo Colpi.
Padova, 01/05/16
Come si può piastrellare un piano nel caso di piastrelle quadrate identiche? E
con piastrelle esagonali? Pentagonali? Come si può ricoprire la superficie più
ampia possibile nell’ultimo caso?
1
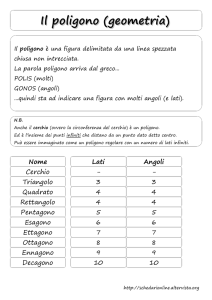
1. Poligoni regolari
Quadrati:
Copertura: 100%
Pentagoni:
Disponendo i pentagoni come in figura, si
nota che a ciascuno di essi corrisponde
un’area non coperta (una delle quali è
evidenziata in giallo). Spostando il punto di
contatto tra vertice del pentagono e lato di
quello adiacente si può minimizzare l’area
gialla
(situazione
descritta
nella
seconda
figura).
In tale configurazione la copertura delle
piastrelle è 92,13%.
Esagoni:
Copertura: 100%
2
2. Numero massimo di lati di un poligono convesso per copertura totale
Sia L il numero di lati, uguale ad A, numero di angoli.
Si ricorda la somma degli angoli interni di un poligono:
Si considera un punto in cui concorrono 3 lati (difatti vogliamo che in ogni
vertice del poligono concorrano esattamente 3 lati). La media degli angoli che
si formano in ogni vertice è 120°1. Dividendo la somma degli angoli interni del
poligono per 120° si ottiene il numero di vertici in cui possono concorrere 3
lati. Questo numero deve essere minore o uguale al numero di vertici del
poligono (
).
Il numero massimo possibile di lati è dunque 6.
1
Si è considerata la media degli angoli poiché la riduzione dell’ampiezza di un angolo di un
poligono comporta l’aumento dell’ampiezza di un altro angolo concorrente nello stesso punto (la
media
è
rimarrà dunque invariata). La media degli angoli massima che si può avere
.
3
Angoli piatti
Sia X il numero di vertici in cui concorrono angoli di media 120°, e Y il
numero di angoli piatti:
{
;
;
;
{
Si può notare che nel caso di un poligono convesso con più di 6 angoli (che
hanno una media di 120° e 180°) il poligono degenera sempre in un esagono.
4
3. Tassello autosimile
Si consideri il pentagono
irregolare a fianco:
Esso
presenta
proprietà
di
la
potersi
replicare con 4 tasselli
simili
a
quello
di
partenza.
Numero di tasselli:
𝑁 𝑛 = 4𝑛
𝑁 0 =1
𝑁 1 =4
𝑁 2 = 16
𝑁 3 = 64
𝑁 4 = 256
5
Il processo di suddivisione può essere ripetuto applicandolo ai sottotasselli
appena creati. In figura, n indica il numero di iterazioni di suddivisione.
Il metodo di divisione qui utilizzato per dividere il tassello in tasselli più
piccoli, può essere utilizzato per crearne di più grandi, andando verso l’esterno
e tassellando così tutto il piano.
Intendendo come periodica una tassellatura in cui ogni tassello può essere
sovrapposto perfettamente ad un altro tramite una traslazione di un vettore
fissato, si può dimostrare che la tassellatura descritta è aperiodica.
Dimostrazione:
La suddetta costruzione si può formalizzare come segue:
A partire dal pentagono P0 si costruisce P1 con 4 tasselli:
1. P0 riflesso rispetto all'asse della base;
2. Tassello 1. traslato verso destra di una base;
3. Tassello 2. ruotato di 180° e traslato;
4. P0 ruotato di 120° in verso orario e traslato.
Definiamo ora ricorsivamente Pn applicando gli stessi punti a Pn-1.
Definiamo macropentagono un qualunque Pn (𝑛 > 0).
Con riferimento alla figura iniziale, si indica con C il vertice collocato più in
alto, con A l'estremo sinistro della base e con B l'estremo destro.
Notiamo che, poiché il primo passo della costruzione consiste in una
riflessione, I punti A e B della base vengono scambiati di posizione ad ogni
iterazione.
6
La fila di tasselli che incontrano la linea di base è costituita dall'alternanza di
tasselli con base giacente sulla linea, tasselli che la toccano con C e da altri
che la toccano con vertici A o B.
La sequenza m di punti A e B giacenti sulla base così individuati (trascurando
i punti C) risponde alla seguente ricorsione:
𝑚2 = 𝐴
𝑚𝑟 = 𝑚𝑟−1 + 𝐴 + 𝑚𝑟−1 𝑠𝑒 𝑟 = 2𝑛;
𝑚𝑟 = 𝑚𝑟−1 + 𝐵 + 𝑚𝑟−1 𝑠𝑒 𝑟 = 2𝑛 + 1.
Inoltre la sequenza dei vertici dei Pn è una alternanza di A e B. In particolare
essi sono punti B se n è pari e A se n è dispari.
Ciò si può dimostrare per induzione:
Passo base: Il vertice C di P1 è A di P0 per il punto 4. della costruzione; tale
punto a sua volta diventa A nella base di P2 per il punto 3. della costruzione.
Il vertice A di P1 è B di P0 per punto 1.; questo a sua volta diventa vertice C
di P2 per punto 4..
Passo induttivo:
 r pari: il vertice C del macrotassello precedente è una A per ipotesi di
induzione e diventa e diventa l'elemento centrale della stringa per punto
3. della costruzione.
La stringa precedente l'elemento centrale coincide con quella ad esso
seguente per punti 1. e 2. della costruzione.
 r dispari: analogo a r pari.
Le stringhe mr sono aperiodiche, perché costituite dalla concatenazione di due
stringhe mr-1 con la frapposizione, alternativamente, di A e B.
7
Se una tassellatura è periodica, si può sempre individuare un parallelogramma
modulo con cui costruire tutta la tassellatura tramite due traslazioni. La retta
s delle basi di Pn è genericamente inclinata di un angolo 𝛼 rispetto alla base
del
parallelogramma
modulo.
Parallelogramma modulo
Si danno tre casi:
(1) La retta s interseca
lati
consecutivi
modulo
in
del
segmenti
commensurabili tra loro,
pertanto
esiste
un
macroparallelogramma
di base m moduli e lato n moduli tale che la retta s stacchi segmenti
congruenti in macroparallelogrammi consecutivi. Dunque, esiste un periodo
nei segmenti individuati dai macroparallelogrammi su s e quindi un periodo
delle stringhe mr, il che è assurdo.
(2) La retta s Interseca
lati
consecutivi
modulo
in
del
segmenti
non commensurabili tra
loro, quindi non esiste
un
macroparallelogramma
come quello del caso (1).
8
Il parallelogramma mostrato in figura è un periodo per ipotesi, pertanto ad
ogni punto di intersezione tra s ed un lato del modulo corrisponde sul lato
opposto l'inizio di una nuova retta di base di macropentagono parallela ad s.
Ciò si ripete per ognuna di queste parallele, che a causa dell'ipotesi iniziale di
incommensurabilità saranno infinite, tutte distinte fra loro; questo implica che
l'altezza dei tasselli sia nulla, il che è assurdo.
(3) La base del parallelogramma modulo giace sulla retta s, ma questo implica
che gli mr sono periodici: assurdo.
Quindi la tassellatura è aperiodica.
9
Regole di produzione del tassello autosimile
A
A-A- A+ A120°
A-
AAA180° A60°+
120°
60°+
A
A180°
A- tassello riflesso rispetto l’asse delle y;
A
60°+
A
60°-
A
A+ tassello riflesso rispetto l’asse delle x;
120°
Aα tassello ruotato in senso orario di un
A+ A+ A- A60°
A60°+
A
A tassello di base;
A180° A180°A A60°-
A+
A
LEGENDA
60°-
angolo α;
A α tassello ruotato in senso antiorario
A120° A120° A60° A60°+
60°
A
A
60°
A
120°
A
di un angolo α.
60°-
A60°+
A120 A120 A60° A-
A60°-
A60° A60° A120°A+
A120°
A60°+ A60°+ A60°-A
A60°
A60°- A60°- A60°+ A60°
A60°
A60°- A60°- A60°+ A180°
Dimostrazioni
A
y=f(x)
A-
y=f(-x)
A+
y=-f(x)
A-
A--=A
y=f(-x)
y=f(x)
A+
A++=A
y=-f(x)
y=f(x)
A+-=A180°
y=-f(-x)
{
Simmetria rispetto l’origine quindi rotazione di 180°
A60°-= A60°-++=A120°+
A120°-=A60+
10
4. Esagoni irregolari
Ipotesi:
Tesi:
(1)
(1) ̂
(2) ̂
̂
̂
̂
̂
̂
̂
(4) ABCDEF è un esagono convesso
(3) ̂
(4) ̂
̂
̂
(5)
(5) ̂
̂
̂
retta (6) ̂
̂
̂
(2)
(3) AB è opposto a DE
Costruzione:
si
tracci
una
passante per i punti D e B.
Dimostrazione:
(1)
̂
somma
̂
di
̂
angoli
per
interni
di
un
triangolo;
(2) ̂
̂ per ipotesi (5);
(3) ̂
̂ per ipotesi (5);
(4)
̂
̂
̂
per
punti (1), (2), (3);
(5) ̂
̂
per ipotesi
(2) e costruzione (coniugati interni di
parallele tagliate da trasversale);
(6) ̂
̂ per ipotesi (5);
(7) ̂
̂
(8) ̂
̂
per punti (5), (6);
̂
per somma dei punti (4) e (7).
Analogamente si dimostrano le altri tesi.
11
5. Quadrilateri irregolari convessi
Ipotesi:
Tesi:
(1)
(1)
(2)
è un quadrilatero convesso
(2)
(3)
Dimostrazione
(1)
(2) ̂
per ip. (1)
̂ per ip. (1)
(3)
per (2) e per angoli alterni interni
congruenti.
Pertanto si può sempre tassellare un piano
partendo da un quadrilatero irregolare convesso
costruendo un esagono con due lati opposti
congruenti e paralleli (vedi sezione 4.).
12
6. Pentagoni irregolari convessi
Ipotesi:
Tesi:
(1)
(1)
(2)
(2)
(3)
(4)
è un pentagono convesso.
Dimostrazione
(1) ̂
̂
per angoli coniugati
interni e ip. (2).
(2) ̂ ̂ per ip. (1).
(3) ̂ ̂
per punti (1) e (2).
(4) Analogamente: ̂ ̂
.
(5)
per (2), (3), (4).
(6)
perché somme di segmenti
congruenti.
Pertanto si può sempre tassellare un piano
partendo
da
un
pentagono
irregolare
convesso con due lati paralleli costruendo
un esagono con due lati opposti congruenti
e paralleli (vedi sezione 4.).
13