LA GIUNZIONE PN
Sulla base delle proprietà chimiche e della teoria di Bohr sulla
struttura dell’atomo (nucleo costituito da protoni e orbitali via via
più esterni in cui si distribuiscono gli elettroni), i materiali si
classificano attraverso il numero atomico nella tavola periodica
degli elementi (tavola di Mendeleev in file separato).
Gli elettroni degli orbitali più esterni vengono detti elettroni di
valenza perché sono quelli che vengono condivisi quando si
instaurano dei legami chimici
Sulla base delle proprietà elettriche i materiali si classificano in:
conduttori
semiconduttori
isolanti
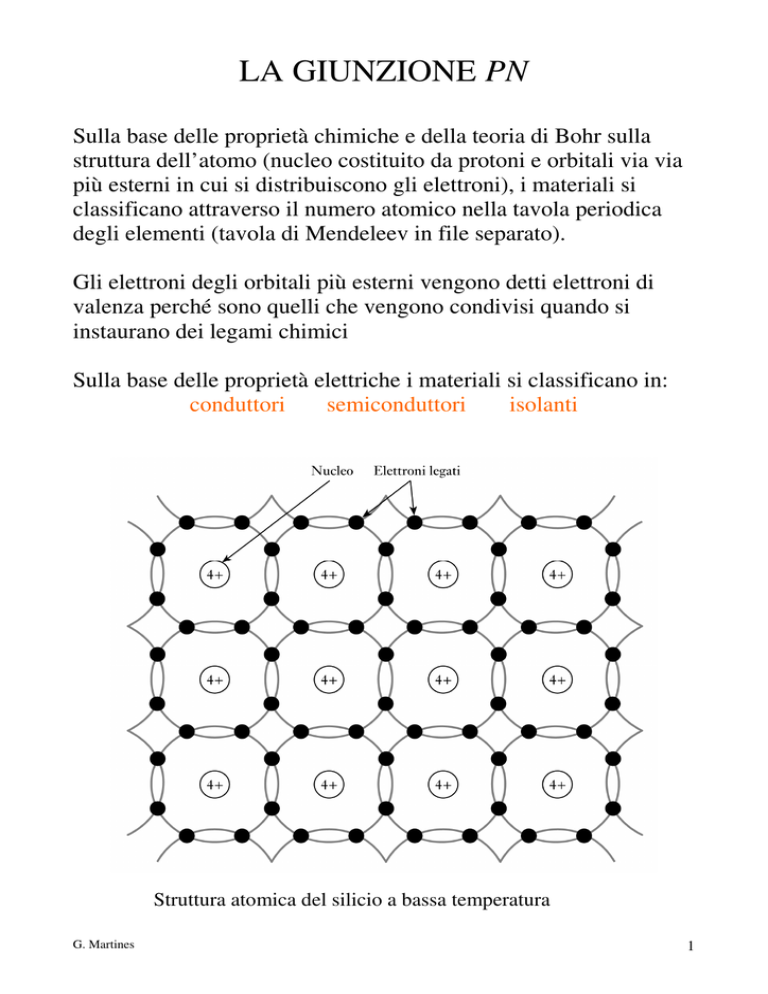
Struttura atomica del silicio a bassa temperatura
G. Martines
1
Conduzione intrinseca
(dipende dalla temperatura)
Struttura atomica del silicio a temperatura ambiente
G. Martines
2
Semiconduttori drogati
Semiconduttore di tipo n:
si ottiene inserendo nella struttura del semiconduttore atomi “donatori”
cioè con un maggior numero di elettroni di valenza (esempio fosforo nel
silicio)
Portatori di carica maggioritari gli elettroni, minoritari le lacune.
Semiconduttore di tipo p:
si ottiene inserendo nella struttura del semiconduttore atomi “accettori”
cioè con un minor numero di elettroni di valenza (esempio boro nel
silicio).
Portatori di carica maggioritari le lacune, minoritari gli elettroni.
La conducibilità estrinseca dipende dalla densità dei droganti.
G. Martines
3
Giunzione pn isolata
∗ Barriera di potenziale: effetto delle cariche fisse
∗ Corrente di diffusione: effetto termodinamico
∗ Corrente di drift: effetto del campo elettrico su portatori
minoritari
∗ All’equilibrio (giunzione isolata) le due correnti devono essere
uguali
G. Martines
4
Giunzione pn polarizzata
L’equazione che esprime la corrente:
G. Martines
eV
I = I S e ηkT − 1
5
Caratteristica vi di una giunzione pn
eV
I = I S e ηkT − 1
I = corrente nella giunzione
IS = corrente di saturazione inversa
e = carica dell’elettrone
k = costante di Boltzman
T = temperatura assoluta (ºK)
η = coefficiente correttivo
η dipende dal materiale semiconduttore ed assume valori compresi fra 1 e 2.
e 11,600
≈
= 40 a 290 0 K
kT
T
G. Martines
NOTA: già per V = 0.1V l’esponenziale vale 54 e
per V = -0.1V l’esponenziale vale 0.02
6
Il diodo a semiconduttore
La corrente in polarizzazione inversa è trascurabile rispetto
quella che si ha in polarizzazione diretta già per valori di V
di qualche decimo di Volt.
a
La caratteristica vi di una giunzione pn approssima quella
di un diodo ideale ma la conduzione si ha per V ≥ VON
G. Martines
7
Circuiti equivalenti del diodo a giunzione pn
G. Martines
8
La caratteristica completa del diodo
G. Martines
9
Analisi di un circuito con diodo
Le equazioni del circuito sono:
I = I S e 40VD
dalla equazione della giunzione pn
E − VD
I=
R
dalla equazione della maglia
Rappresentazione delle equazioni sul piano VI della caratteristica del diodo.
G. Martines
10
Il concetto retta di carico e di punto di lavoro
La corrente nella maglia deve essere unica e ID è l’unico valore della corrente nel diodo che
soddisfa questa condizione perché ordinata del punto di intersezione delle due curve.
Il punto di lavoro (o punto di riposo) è la soluzione del sistema di equazioni in DC.
G. Martines
11
Scelta del modello equivalente
I=
G. Martines
E − VON
R + rON
12
Effetti della temperatura
Dalla espressione della corrente nella giunzione pn discende immediatamente che la tensione ai capi
della giunzione può essere espressa da:
A parità del rapporto I/IS la tensione aumenta al crescere della
kT
T
V
=
≅
temperatura come la tensione termica T
kT I
e 11600 ma anche la
V =
ln + 1
corrente IS cresce con la temperatura perché aumenta la velocità di
e IS
generazione di coppie elettrone-lacuna; nel silicio IS all'incirca raddoppia
ogni 10°C di aumento della temperatura
In conclusione la tensione V ai capi di una
giunzione pn in silicio, a parità di corrente I,
diminuisce di circa 2 mV/°C
all’aumentare della temperatura.
G. Martines
13
Diodo Zener
È un diodo progettato per funzionare nella regione di break down della caratteristica VI.
Il diodo funziona in polarizzazione inversa ma la corrente cresce per
due meccanismi:
Effetto ZENER: il campo elettrico è abbastanza intenso da staccare
elettroni dalla banda di valenza (regione di carica spaziale molto
stretta).
Prevalente fino a 5V.
La VBR diminuisce (poco) al crescere della temperatura.
Moltiplicazione a valanga: gli elettroni nella regione di carica spaziale
vengono accelerati a tal punto che gli urti con il reticolo provocano
ionizzazione degli atomi (regione di carica spaziale ampia).
Prevalente da >5V ad alta tensione.
La VBR cresce al crescere della temperatura.
Tipicamente i coefficienti di temperatura sono compresi tra 0.001% e
0.1% per °C.
G. Martines
14
Altri diodi di uso comune
1. Diodo Schottky. È basato su una giunzione metallo-semiconduttore e non su una
giunzione pn. La corrente è costituita solo da portatori maggioritari. La tensione di
accensione è circa 0.25V.
2. Diodo tunnel. È basato su una giunzione pn con
densità di drogaggio molto alte per avere una regione
di carica spaziale così sottile da generare una
conduzione per effetto tunnel. Utilizzato come
oscillatore a resistenza negativa
3. Diodo varactor. Si sfrutta la capacità variabile
associata alla regione di carica spaziale di una
giunzione pn in polarizzazione inversa. Facendo
variare la tensione di polarizzazione inversa si fa variare la larghezza della regione di
svuotamento e quindi si ottiene una capacità variabile controllata dalla tensione
applicata.
G. Martines
15
4. Fotodiodo. Se si illumina la regione di carica spaziale di una giunzione pn polarizzata
inversamente, i fotoni di specifiche lunghezze d’onda vengono catturati e si generano
coppie elettrone-lacuna che fanno aumentare la corrente inversa della giunzione.
5. LED (light-emitting diode). Quando una giunzione pn viene polarizzata direttamente
conduce corrente ed il flusso di portatori di carica incrementa il tasso di ricombinazione
delle coppie elettrone-lacuna. La ricombinazione porta ad una emissione di fotoni con
l’energia che si rende disponibile (effetto di elettroluminescenza). La lunghezza d’onda
dei fotoni dipende dal gap di energia fra le bande di conduzione e di valenza del
materiale su cui la giunzione viene realizzata. Nel silicio la transizione non tende a
generare fotoni ma altri materiali generano fotoni nell’infrarosso, nel visibile o
nell’ultravoletto. Tipicamente la tensione in conduzione è compresa fra 1V e 2V con
correnti di qualche mA.
6. Diodo laser. La giunzione pn viene utilizzata per generare fotoni, come nei LED, ma
all’interno di una struttura che ha anche un guadagno ottico; così si innesca il fenomeno
della emissione stimolata, cioè la produzione di fotoni con la stessa frequenza,
polarizzazione e fase dei fotoni che la hanno provocata, che da’ luogo al processo di
rigenerazione coerente su cui si basa il laser. Sono quindi sorgenti di luce coerente
anche di elevata potenza.
G. Martines
16
Raddrizzatore a semplice semi-onda
G. Martines
17
G. Martines
18
Per scrivere le equazioni del circuito consideriamo la figura di merito costituita dalla
tensione di ripple che in prima approssimazione può essere espressa da:
Vr ≅
(VP − VON ) T
RL
C
in pratica si è assunto che la corrente sul carico non vari significativamente durante la
scarica del condensatore e quindi possa essere espressa dal primo fattore dell’equazione;
in questa ipotesi la Vr è pari alla variazione di tensione ai capi della capacità per effetto di
una scarica a corrente costante IDC per un tempo T , cioè
∆V =
I DC
T
C
perché l’assunzione possa considerarsi valida deve essere RC >> T .
G. Martines
19
Raddrizzatore a doppia semionda
(ponte di Graetz)
Vr ≅
G. Martines
(VP − 2VON )
RL
T
2C
20
Diodi limitatori
G. Martines
21
Diodi limitatori
Diodi di contenimento
Un esempio di applicazione dei diodi limitatori come
protezione dalla sovratensioni.
G. Martines
22
Circuiti di aggancio
(clamping o DC restorer)
-
G. Martines
23
Un semplice generatore di tensione costante
Un esempio di applicazione del diodo zener.
A circuito aperto, se V> VZ ed R è scelta in modo che
V − VZ
> I ZK
R
allora VO=VZ.
In presenza di un carico RL si avrà VO = V Z per tutti i
valori di RL tali che
V − V Z VO
−
> I ZK
R
RL
Si noti che le relazioni possono essere lette anche in
termini della variazione V.
G. Martines
24
Duplicatore di tensione
G. Martines
25