Logica Numerica – Approfondimento 1
E. Barbuto
Minimo Comune Multiplo e Massimo Comun Divisore
Il concetto di multiplo e di divisore
Considerato un numero intero n, se esso viene moltiplicato per un numero a, si ricava un nuovo
numero b che è multiplo del numero di partenza n.
Ad esempio, considerato il numero 12, se esso viene moltiplicato per 2 si otterrà 12×2=24. 24 è un
multiplo di 12. Analogamente, moltiplicando 12 per 3, si otterrà 12×3=36, un nuovo multiplo di 12.
Notiamo che da 12×2=24 si deduce che 24:2=12. In tal caso si può dire che 2 è un divisore di 24 ed
anche che 24 è divisibile per 2.
Il divisore di un numero intero n è quel numero a tale che, se n viene diviso per esso, si ottiene un
quoto b e tale divisione presenta resto nullo.
Calcoliamo ora dei divisori del numero 12. Abbiamo che se esso viene diviso per 6 si ottiene
12:6=2, senza alcun resto. Questo vuol dire che 6 è un divisore di 12. Parimenti, si può dividere 12
per 4 ed ottenere 12:4=3 (con resto nullo). Questo vorrà dire che anche 4 è un divisore di 12. Si noti
inoltre come, ad esempio, 12:8=1 con resto pari a 4. Il resto non nullo ci indica che 8 non è un
divisore di 12.
Stabiliamo inoltre che un numero che è divisibile solo per se stesso e per 1 è detto numero primo.
Ad esempio 7 è divisibile solo per 7 e per 1, per cui esso è numero primo.
Il Minimo Comune Multiplo
Il minimo comune multiplo (mcm) di due numeri interi a e b è il più piccolo intero positivo che è
multiplo sia di a che di b.
Quindi, detto m il mcm di a e b, avremo che esistono due numeri interi n1 ed n2 tali che, moltiplicati
per a e b ci restituiscono m:
m = a ⋅ n1
m = b ⋅ n2
Inoltre m gode della proprietà di essere il numero più piccolo possibile perché questo possa
avvenire.
Notiamo che dalle due relazioni precedenti si deduce che:
m
= n1
m : a = n1
a
o, se vogliamo,
m : b = n2
m
= n2
b
Cioè m è un numero tale che, se diviso per i numeri a e b, restituisce i due numeri interi n1 ed n2 e
questa divisione non produce alcun resto. Possiamo quindi dire che a e b sono dei divisori di m.
Inoltre m è il numero più piccolo possibile perché questo possa avvenire.
Un esempio può aiutare a chiarirci le idee.
Consideriamo due numeri:
a=6
b=8
Ci proponiamo di calcolare il mcm di questi due numeri e proviamo dapprima a vedere se il numero
12 è un buon candidato.
Abbiamo che:
12 : 6 = 2
12 : 8 = 1 resto = 4
Il numero 12 è un multiplo di 6 ma non di 8, infatti la divisione per quest’ultimo numero produce
un resto di 4.
Proviamo ora con il numero 48:
48 : 6 = 8
48 : 8 = 6
Notiamo che 48 è un buon candidato per essere il mcm in quanto è un multiplo sia di 6 che di 8 (le
due divisioni non danno resto).
Il numero 48 non è, però, il numero più piccolo possibile per cui questo avviene. Infatti il numero
24 ha la stessa proprietà di essere multiplo sia di 6 che di 8.
24 : 6 = 4
24 : 8 = 3
Effettivamente 24 è il numero più piccolo possibile per il quale questo avviene quindi esso è il
minimo comune multiplo tra 6 ed 8. Scriveremo:
mcm(6;8)=24.
Ovviamente, in maniera analoga, il mcm è definibile anche per più di due numeri.
Algoritmo della fattorizzazione per il calcolo del mcm
Per il calcolo del mcm di alcuni numeri è necessario scomporre i numeri in questione. Scomporre
un numero vuol dire trasformarlo in un prodotto costituito da fattori che sono tutti numeri primi
elevati a determinati esponenti.
Ad esempio, consideriamo tre numeri, 36, 28, 15 e partiamo con lo scomporre il 36:
36 2
18 2
9 3 36 = 2 ⋅ 2 ⋅ 3 ⋅ 3 = 22 ⋅ 32
3
3
1
Nell’iniziare la scomposizione abbiamo scritto a destra del 36 il numero 2 per il quale esso è
divisibile e, sotto al numero 36, il numero 18 che è il risultato della divisione 36:2. Di fianco al 18
abbiamo riscritto il numero 2 per il quale esso è divisibile e così abbiamo continuato fino a
scomporre totalmente il numero, giungendo ad 1 e considerando nelle divisioni solo numeri primi
(nella fattispecie 2 e 3).
Di fianco alla scomposizione abbiamo riassunto il risultato: 36=22⋅32.
Lo stesso possiamo fare per gli altri due numeri:
28 2
14 2
28 = 2 ⋅ 2 ⋅ 7 = 22 ⋅ 7
7 7
1
15 3
5
1
5 15 = 3 ⋅ 5
Per determinare il mcm tra i tre numeri dobbiamo prendere in considerazione i fattori comuni e non
comuni con l’esponente massimo.
36 = 22 ⋅ 32
28 = 22 ⋅ 7
15 = 3 ⋅ 5
Il 2 ed il 3 compaiono con un esponente massimo pari a 2, quindi sceglieremo 22⋅32 . Inoltre
consideriamo anche il 5 ed il 7 che compaiono in forma semplice.
Abbiamo perciò il prodotto dei seguenti fattori.
Mcm(36;28;15) = 22⋅32⋅5⋅7 = 1260
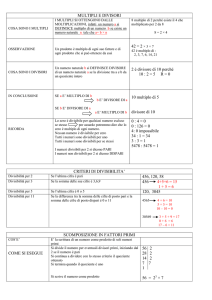
Quesiti Risolti
Un quesito basilare, che richiede il semplice calcolo di un mcm, può essere il seguente:
Quanto vale il minimo comune multiplo dei numeri 16, 4 e 9?
A. 576
B. 144
C. 16
D. 64
E. 90
Scomponiamo i tre numeri:
16 2
8 2
4 2 16 = 2 ⋅ 2 ⋅ 2 ⋅ 2 = 24
4 2
2 2 4 = 2 ⋅ 2 = 22
9 3
3 3 9 = 3 ⋅ 3 = 32
1
1
2 2
1
Raccogliendo i fattori comuni e non comuni con il massimo esponente abbiamo:
mcm(16;4;9) = 24⋅32= 144 (Risposta B)
Di seguito proponiamo invece un quesito tipico di logica nel quale bisogna mettere a frutto la
definizione del minimo comune multiplo in un contesto pratico.
Tre commessi viaggiatori si recano a Napoli rispettivamente ogni 8, ogni 12 e ogni 10 giorni.
Essendosi trovati in quella città nello stesso giorno, dopo quanti giorni si ritroveranno ancora
insieme?
A. 120 giorni
B. 60 giorni
C. 80 giorni
D. 100 giorni
E. 96 giorni
I tre commessi viaggiatori si sono incontrati insieme in un determinato giorno. Il primo commesso
sarà di nuovo a Napoli dopo 8 giorni dal giorno in questione, poi dopo 16 giorni dal giorno in
questione, poi dopo 24 giorni e così via… In generale giungerà a Napoli dopo un numero di giorni
che è multiplo di 8. Il secondo commesso giungerà nuovamente a Napoli dopo un numero di giorni
che è un multiplo di 12, mentre il terzo dopo un numero di giorni che è un multiplo di 10. Quindi,
perché i tre possano incontrarsi, dovrà trascorrere un numero di giorni pari ad un multiplo in
comune tra i tre numeri (8, 10 e 12). Se vogliamo il numero minore possibile di giorni che dovranno
trascorrere allora dobbiamo calcolare il minimo comune multiplo.
Abbiamo:
8 = 23
12 = 22 ⋅ 3
10 = 2 ⋅ 5
Per cui:
mcm(8;12;10) = 23⋅3⋅5= 120 (Risposta A)
Il Massimo Comun Divisore
Il massimo comun divisore (MCD) di due numeri interi a e b, che non siano entrambi uguali a zero,
è il numero naturale più grande per il quale possono essere entrambi divisi.
Quindi, detto m il MCD di a e b, possiamo indicare rispettivamente con n1 ed n2 il quoto delle due
divisioni:
a : m = n1
b : m = n2
È importante sottolineare che il resto di entrambe le divisioni è nullo e che m gode della proprietà di
essere il numero maggiore possibile per il quale dividere entrambi i numeri interi a e b, ottenendo
un resto nullo.
Anche in questo caso un esempio può chiarirci le idee.
Consideriamo due numeri:
a=6
b=8
Notiamo che 6 è divisibile (cioè può essere diviso senza ottenere resto) per 6, 3, 2 e 1, mentre 8 può
essere diviso (anche questa volta senza ottenere resto) per 8, 4, 2, e 1. Il numero più alto possibile
che divide ambo i numeri è quindi 2.
Per questo motivo scriviamo:
MCD(6;8)=2.
Ovviamente, in maniera analoga, il MCD è definibile anche per più di due numeri.
Due numeri si dicono coprimi o primi tra loro se il loro massimo comun divisore è uguale a 1. Per
esempio, i numeri 9 e 28 sono primi tra loro. Infatti 9 è divisibile per 9, 3 e 1, mentre 28 è divisibile
per 28, 14, 7, 4, 2 e 1. Notiamo che il divisore in comune più alto possibile è proprio 1.
MCD(9;28)=1.
Algoritmo della fattorizzazione per il calcolo del MCD
Per il calcolo del MCD di alcuni numeri è necessario nuovamente scomporre i numeri in questione.
Questa volta consideriamo i tre numeri: 24, 28, 20 e scomponiamoli:
24 2
28 2
12 2
14 2
28 = 2 ⋅ 2 ⋅ 7 = 22 ⋅ 7
6 2 24 = 2 ⋅ 2 ⋅ 2 ⋅ 3 = 23 ⋅ 3
7 7
3 3
1
1
20 2 ⋅ 5
2
1
2
20 = 22 ⋅ 5
Per determinare il MCD tra i tre numeri dobbiamo prendere solo i fattori comuni con l’esponente
minimo.
24 = 23 ⋅ 3
28 = 22 ⋅ 7
20 = 22 ⋅ 5
Il 2 è l’unico fattore che compare nella scomposizione di tutti e tre i numeri con un esponente
minimo pari a 2, quindi sceglieremo 22.
Abbiamo perciò il seguente MCD.
MCD(24;28;20) = 22 = 4
Algoritmo di Euclide per il calcolo del MCD
L’algoritmo di Euclide è un metodo per il calcolo veloce di un MCD tra due numeri attraverso
divisioni successive. Tale metodo permette di guadagnare tempo se i due numeri hanno un valore
abbastanza alto e la loro scomposizione risulterebbe spesso lunga e talvolta impraticabile.
Descriviamo l’algoritmo con un esempio. Consideriamo i seguenti due numeri: 3575 e 1620.
Iniziamo con il dividere il numero più grande 3575 per quello più piccolo 1620. Per compiere tale
divisione in modo veloce possiamo pensare a quante volte il 1620 è contenuto in 3575. Ovviamente
1620 è sicuramente contenuto una sola volta nel 3575, di seguito lo moltiplichiamo per 2 per capire
se è contenuto due volte: 1620×2=3240. Ci fermiamo a questo punto poiché capiamo che
moltiplicare 1620 per 3 ci porterebbe ad un numero superiore a 3575. Per calcolare il resto della
divisione basta calcolare la seguente sottrazione: 3575-3240=335.
Quindi possiamo scrivere schematicamente:
3575=1620×2+335
Dobbiamo ora compiere il secondo passaggio dell’algoritmo, calcolando la nuova divisione tra il
numero 1620, divisore del passaggio precedente, ed il resto 335. Notiamo che 335×5=1675 che
supera 1620, mentre 335×4=1340 che è contenuto nel 1620. Il nuovo resto sarà 1620-1340=280.
Riassumiamo quindi i due primi passaggi compiuti e, schematicamente, descriviamo i passaggi
successivi:
3575
=
1620
×2 +
335
1620
=
335
×4 +
280
335
=
280
×1 +
55
280
=
55
×5 +
5
55
=
5
×11
0
MCD(3575;1620)=5
Come si nota dallo schema che riassume i passaggi, ad un certo punto la divisione dà resto pari a
zero (55=5×11+0). A quel punto l’algoritmo si arresta e l’ultimo resto non nullo, che si trova nel
passaggio precedente ed è pari a 5, costituisce il MCD dei due numeri presi in considerazione.
Quindi:
MCD(3575;1620)=5
Quesiti Risolti
Un quesito basilare, che richiede il semplice calcolo di un MCD, può essere il seguente:
Quanto vale il massimo comun divisore dei numeri 12, 4 e 20?
A)
5
B)
2
C)
4
D)
6
E)
10
Scomponiamo i tre numeri:
12 2
4 2
20 2 ⋅ 5
6 2
2
2
12 = 2 ⋅ 3
2 2 4=2
2
2 20 = 22 ⋅ 5
3 3
1
1
1
Raccogliendo i fattori comuni con il minimo esponente abbiamo:
(Risposta C)
MCD(12;4;20) = 22= 4
Di seguito proponiamo invece un quesito tipico di logica nel quale bisogna mettere a frutto la
definizione del massimo comun divisore in un contesto pratico.
Quattro libri che hanno rispettivamente 208, 192, 240 e 304 pagine, devono comporsi in fascicoli
aventi ciascuno lo stesso numero di pagine. Qual è il massimo numero di pagine che può avere ogni
fascicolo?
A)
16
B)
12
C)
14
D)
6
E)
10
Per creare una serie di fascicoli da un libro costituito da un certo numero di pagine occorre che i
fascicoli abbiano un numero di pagine pari ad un divisore del numero totale di pagine del libro. Ad
esempio il libro con 208 pagine può essere scomposto in due fascicoli da 104 pagine (104 è un
divisore di 208) oppure in 4 fascicoli da 52 pagine (52 è ancora un divisore di 208). Lo stesso
discorso vale per gli altri tre libri. Per creare, però, dei fascicoli, per ognuno dei quattro libri, che
abbiano lo stesso numero di pagine, facendo in modo che questo sia il maggiore possibile, è
necessario calcolare il massimo comun divisore dei quattro numeri di pagine presenti nei quattro
libri.
192 2
240 2
208 2
304 2
96 2
120 2
152 2
104 2
48 2
60 2
76 2
52 2
24 2
240 = 24 ⋅19
208 = 26 ⋅ 3 30 2 240 = 24 ⋅ 3 ⋅ 5
208 = 24 ⋅13
38 2
26 2
12 2
15 3
6 2
19 19
13 13
5 5
1
1
3 3
1
1
Per cui:
MCD(208;192;240;304) = 24= 16 (Risposta A)
Esercizi
1) Un fioraio deve utilizzare 28 rose e 36 garofani per preparare alcuni mazzi contenenti ciascuno lo
stesso numero di fiori, tutti dello stesso tipo. Qual è il massimo numero di fiori di ciascun mazzo?
12
A)
4
B)
6
C)
7
D)
2
E)
2) Quanto vale il Massimo Comune Divisore dei numeri 105, 21 e 63?
3
A)
7
B)
21
C)
105
D)
63
E)
3) Due motociclisti partono insieme per una corsa su una pista: il primo compie un giro ogni 20
secondi e il secondo ogni 30 secondi. Dopo quanto tempo si troveranno a passare insieme per la
prima volta sulla linea di partenza?
60 secondi
A)
600 secondi
B)
120 secondi
C)
100 secondi
D)
90 secondi
E)
4) Dalla stazione di Napoli alle 8.00 partono contemporaneamente due treni, uno diretto a Roma e
l’altro a Bari. Sapendo che da Napoli un treno per Roma parte ogni 2 ore e un treno per Bari parte
ogni 5 ore, dopo quante ore due treni ripartiranno insieme da Napoli per le stesse stazioni?
10 ore
A)
7 ore
B)
20 ore
C)
5 ore
D)
2 ore
E)
5) Quanto vale il minimo comune multiplo dei numeri 12, 15 e 8?
124
A)
110
B)
C)
D)
E)
118
120
60
Risposte corrette
1) B
2) C
3) A
4) A
5) D
Soluzioni
1) Siccome i mazzi devono contenere tutti lo stesso quantitativo di fiori, tutti dello stesso tipo (o
solo rose o solo garofani) allora dovremo riferirci ai divisori di 28 (il numero di rose) e di 36 (il
numero di garofani) per conoscere quanti fiori possono essere contenuti in ogni mazzo. In
particolare con i divisori comuni potremo individuare il numero di fiori che possono essere
contenuti in ciascun mazzo, facendo in modo che i mazzi di rose e di garofani abbiano lo stesso
quantitativo di fiori. Infine con il massimo comun divisore individueremo il numero massimo di
fiori con i quali possiamo costituire questi mazzi.
Calcoliamo il massimo comun divisore di 28 e 36:
36 2
28 2
18 2
14 2
2
28 = 2 ⋅ 7
9 3 36 = 22 ⋅ 32
7 7
3 3
1
1
2
Il massimo comun divisore è MCD(28;36)=2 =4. Quindi ognuno dei mazzi (sia esso costituito da
soli garofani o da sole rose) conterrà 4 fiori.
2) Calcoliamo il MCD dei tre numeri:
105 5
63 3
21 3
21 3
21 3
7 7 21 = 3 ⋅ 7
105 = 5 ⋅ 3 ⋅ 7
105 = 32 ⋅ 7
7 7
7 7
1
1
1
Raccogliendo i due fattori in comune (3 e 7) con il minimo esponente avremo che il massimo
comun divisore è MCD(105;21;63)=3⋅7=21
3) Il primo motociclista passerà sulla linea di partenza dopo 20 secondi, poi dopo 40, poi ancora
dopo 60 e così via… In generale il suo passaggio avverrà dopo che sono trascorsi un numero di
secondi pari ad un multiplo di 20. Il passaggio del secondo motociclista avverrà dopo che sono
trascorsi un numero di secondi pari ad un multiplo di 30. Quindi, quando saranno passati un numero
di secondi pari ad un multiplo sia di 20 che di 30, avremo il passaggio contemporaneo dei due
motociclisti sulla linea di partenza. Per avere il numero minimo di secondi entro il quale entrambi
passeranno sulla linea di partenza dobbiamo calcolare il minimo comune multiplo di 20 e 30.
Abbiamo:
30 = 2 ⋅ 3 ⋅ 5
20 = 22 ⋅ 5
Per cui, raccogliendo fattori comuni e non comuni con il massimo esponente, abbiamo:
mcm(30;20) = 3⋅5⋅22= 60 secondi
4) I treni per Roma partono quando sono trascorse un numero di ore pari ad un multiplo di 2, mentre
i treni per Bari partono dopo un numero di ore trascorse pari ad un multiplo di 5. I multipli in
comune, tra 2 e 5, rappresentano il numero di ore trascorse dopo le quali partono
contemporaneamente sia il treno per Roma che quello per Bari. In particolare il minimo comune
multiplo rappresenta il numero minimo di ore che bisogna attendere perché partano
contemporaneamente sia il treno per Roma che quello per Bari.
Il minimo comune multiplo tra 2 e 5 è semplicemente il prodotto dei due numeri:
mcm(2;5)=2⋅5=10. Bisognerà attendere 10 ore.
5) Calcoliamo il mcm dei tre numeri:
12 3
8 2
15 3
4 2
4 2
5 5 15 = 3 ⋅ 5
12 = 3 ⋅ 22
8 = 23
2 2
2 2
1
1
1
Per cui, raccogliendo fattori comuni e non comuni con il massimo esponente, abbiamo:
mcm(12;15;18) = 3⋅5⋅23= 120