a) Quando un campo elettrico è diretto verso il basso, il punto B è ad

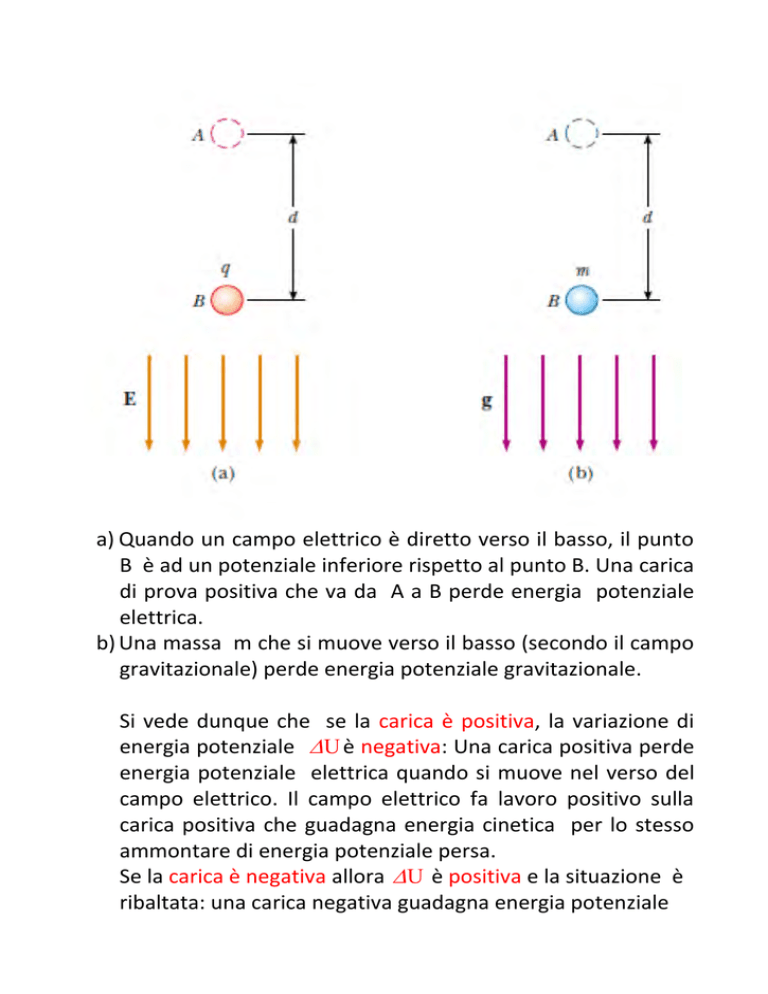
a) Quando un campo elettrico è diretto verso il basso, il punto
B è ad un potenziale inferiore rispetto al punto B. Una carica
di prova positiva che va da A a B perde energia potenziale
elettrica.
b) Una massa m che si muove verso il basso (secondo il campo
gravitazionale) perde energia potenziale gravitazionale.
Si vede dunque che se la carica è positiva, la variazione di
energia potenziale  U è negativa: Una carica positiva perde
energia potenziale elettrica quando si muove nel verso del
campo elettrico. Il campo elettrico fa lavoro positivo sulla
carica positiva che guadagna energia cinetica per lo stesso
ammontare di energia potenziale persa.
Se la carica è negativa allora  U è positiva e la situazione è
ribaltata: una carica negativa guadagna energia potenziale
quando si muove nel verso del campo elettrico. Se la carica
negativa è rilasciata da fermo nel campo elettrico, essa
accelera nel verso opposto a quello del campo elettrico.
Nel caso di distribuzione continua di carica si dovrà calcolare
V0 ( P ) 
1
dq
 ( x , y, z )dxdydz

4 0  r
4 0 
r
1
Ricordando che
E   grad (V0 )
e la forma differenziale del teorema di Gauss per l’elettrostatica
 
div ( E ) 
0


div ( E )   divgrad (V0 ) 
0
Ossia
 V0  V0  V0

V0  2  2  2  
0
x
y
z
2
Nota come
2
2
equazione di Poisson.
Se si impone la condizione che il potenziale si annulli all’infinito
almeno come 1/r e che il campo si annulli all’infinito almeno
come 1/r2 l’equazione si può integrare una volta nota la
distribuzione  ( x, y, z) delle cariche che generano il campo. Si
trova che la soluzione è proprio la
1
dq
1
 ( x , y, z )dxdydz
V0 ( P ) 

4 0  r
4 0 
r
Nei punti dello spazio esterni ai conduttori   0 e l’equazione
si riduce a:
 2V0  2V0  2V0
V0 


0
2
2
2
x
y
z
Nota come equazione di Laplace
Potenziale dovuto a due cariche sorgenti
q=
q2 > 0
1
q1
q2
V=
( x) k
+k
|x|
|x−a|