Le Disequazioni di qualunque grado e tipologia

LE DISEQUAZIONI
Le Disequazioni di qualunque grado e tipologia
( sintesi teorica per recupero con alcuni esempi significativi )
Prerequisiti:
Disequazioni di Primo Grado
Fattorizzazione di Polinomi di Qualunque Grado
Teorema di Ruffini ( scomposizione )
I metodi comunemente utilizzati sono sicuramente degli ottimi strumenti. Il Metodo
delle Parabole, ad esempio, risolve problemi di disequazioni di 2° grado, ma non è ben
utilizzabile in altri casi. Per questi motivi provo a generalizzare il problema introducendo
due metodi che utilizzeremo nei casi specifici e nelle forme miste. Questi strumenti,
sono semplici ed intuitivi dà capire, nonché logici nel senso più matematico. Non vi è nulla
di nuovo se non una risistemazione sistemica degli argomenti.
Gli studenti, sovente, non sanno ( pur conoscendo i metodi ) quale strumento sia più
idoneo dà utilizzare. Ciò si risolve con chiare regole iniziali e con tanti esercizi.
I Metodi S/N e +/- come strumenti di risoluzione delle Disequazioni. Questi due metodi
sono equivalenti in struttura, ma non in logica. Si compongono di due parentesi (
Domanda e Risposta ) ed un grafico risolutivo ( intersezione o prodotto delle Soluzioni ).
Sommario:
Il Metodo S/N
Il Metodo +/-
Disequazioni Lineari
Disequazioni Fratte
Metodo Misto {S/N} U {+/-}
Disequazione Irrazionale
Disequazione con Valore Assoluto
Il Metodo S/N
( sommario )
Per metodo S/N si intende SI e NO, ove sono verificate un insieme di disequazioni e
dove non lo sono; …. prima di tutto costruiamo due parentesi graffe; la prima contenente
le linee disequazioni ( la chiamiamo Domanda ) e la seconda contenente le soluzioni ( la
chiamiamo Risposta ), linea per linea:
quindi, dato un insieme di disequazioni ( che chiamiamo linee ):
la DS/N
1


 2



 ...
n
 

si costruisce, linea per linea l’insieme delle risposte RS/N
R1
 
 R2
 

 ...
Rn
 
Quindi si riportano i dati, linea per linea, in un Grafico opportuno:
si riportano su di una retta orientata i n valori delle risposte …
S/N
Rx
x1
N
N
. . .
. . .
N
xn
x2
S
N
. . .
. . .
N
S
S
. . .
. . .
N
S
S
. . .
. . .
S
( spazio soluzione )
… e si incrociano i SI con i NO …. E solo negli intervalli contenenti i SI, si può ritenere
lo spazio come soluzione, … in pratica dove tutte le linee sono soddisfatte.
Sistema di Diseq. Lineari come esempio del Metodo S/N
( sommario )
Svolgiamo un semplice esempio col seguente Sistema:
2 x  3  2

S  5  3x  1
non in forma normale ( il testo o il problema )
4 x  5  0

lo portiamo in forma normale:

x 
2x  1  0
2x  1  0



SN 3x  4  0 che chiamiamo Domanda: DS/N 3x  4  0 e risposta RS/N  x 

4 x  5  0
4 x  5  0


x 

1
2
4
3
5
4
In questo metodo leggiamo la domanda e poi la risposta per costruire il relativo Grafico
con tre linee ( tante quante le disequazioni ). Ovvero …. La prima linea è soddisfatta per
1
x  ; la seconda linea è soddisfatta per … e così via.
2
Quindi costruiamo il GRAFICO DELLE SOLUZIONI:
S/N
Rx
1
2
N
N
N
5
4
S
N
N
4
3
S
N
S
S
S
S
( spazio soluzione )
ne segue che il sistema di disequazioni risulta soddisfatto in un intervallo illimitato a
destra che possiamo rappresentare nei seguenti modi:
4
x

3
4


 3 ;  dove con la “(“ intendiamo la non appartenenza all’insieme soluzione
4
dell’estremo , mentre per “]” intendiamo l’appartenenza dell’estremo all’insieme.
3
Esercizi … Teoria e TEST
Matematica  Parte III Algebra  Disequazioni Algebriche
Il Metodo +/-
( sommario )
Per metodo +/- si intende + per – o + diviso -, ove ogni disequazioni è di grado sup al 1°
DEF. ( Grado o Numero Max Fattori )
[ per grado di una disequazioni, o numero massimo di fattori irriducibili, intendiamo la
somma dei gradi max di ogni singolo fattore o polinomio irriducibile ]
Si creano due parentesi graffe: la prima contenente le linee disequazioni determinate
dai singoli fattori della scomposizione ( la chiamiamo Domanda ) e la seconda contenente
le soluzioni ( la chiamiamo Risposta ), linea per linea. :
quindi data una Disequazione Iniziale di grado superiore al primo di n-fattori con
richiesta:
Disequazione Iniziale  0 o Disequazione Iniziale  0
Disequazione Iniziale >0 o Disequazione Iniziale <0
la D+/-
1


 2



 ...
n
 

si costruisce, linea per linea l’insieme delle risposte R+/-
R1
 
 R2
 

 ...
Rn
 
Quindi si riportano i dati, linea per linea, in un Grafico opportuno:
si riportano su di una retta orientata i n valori delle risposte …
Quindi costruiamo il GRAFICO DELLE SOLUZIONI:
+/-
Rx
x1
xn
x2
+
-
+
+
+
+
+
+
+
( spazio soluzione + )
( spazio soluzione - )
( spazio soluzione + )
( spazio soluzione - )
… e si moltiplicano i + e i –, per ogni intervallo, ottenendo così degli intervalli soluzione
+ e degli intervalli soluzione -. Allora gli intervalli soluzione saranno determinati dalla
Disequazione Iniziale. Infine per definire gli estremi degli intervalli valutiamo se essi
siano o no contenuti.
Le Disequazioni Fratte come esempio del Metodo +/-
( sommario )
Svolgiamo un esempio con una disequazioni fratta di 3° grado:
(19 x  6 x ²  15)
(2 x  3)(5  3x)
 0 il testo viene fattorizzato come segue
0
(4 x  5)
(4 x  5)
3

x

2
2 x  3  0

5

D+/- 5  3x  0
e risposta
R+/-  x 
3

4 x  5  0

x  5

4
La Domanda determina il Segno ( + o - ) e la Risposta il Verso ( destra o sinistra )
3
3
nel senso: la prima riga la leggo > e quindi + …. per x  e quindi alla destra di ;
2
2
5
5
la seconda riga la leggo > e quindi + …. per x  e quindi alla sinistra di ; e così via.
3
3
Quindi costruiamo il GRAFICO DELLE SOLUZIONI:
+/-
Rx
5
4
3
2
+
-
+
+
+
-
( spazio soluzione )
5
3
+
+
+
+
+
+
-
( spazio soluzione )
ne segue che la disequazioni risulta soddisfatta nei due intervalli che possiamo
rappresentare nei seguenti modi:


3
5
5
x e x
2
3
4
5
3 5 
 2 ; 3     ; 4 
La difficoltà sta sicuramente nella fattorizzazione dei polinomi e nella determinazione
del segno e relativo verso di ogni linea. Con un bel numero di esempi e casi si impara
abbastanza bene la procedura.
Esercizi … Teoria e TEST
Matematica  Parte III Algebra  Disequazioni Algebriche
Disequazione Irrazionale
( sommario )
Ve ne sono di due tipi in Forma Normale:
(1) A( X )  B( X )
(2) A( X )  B( X )
Sintetizziamo la Teoria:


se l’indice di radice è dispari …. Si eleva per togliere la radice e si risolve col
Metodo +/se l’indice di radice è pari … si distinguono i due casi:
caso (1) esempio caso (1)
1.
2.
3.
A(X) > 0 per il C.E. del radicando
B(X) > 0 per ché A(X ) non può essere un numero negativo
A( X )  B( X ) fattorizzandola si risolve col Metodo +/- e si riportano
p
gli intervalli soluzione della linea nel Sistema Risposta
caso (2) esempio caso (2)
1.
2.
Se B(X) < 0 allora basta che A(X) > 0 per il C.E. del radicando
p
Se B(X) > 0 allora A( X )  B( X ) fattorizzandola si risolve col Metodo
+/- e si riportano gli intervalli soluzione della linea nel Sistema Risposta
3. La soluzione sarà l’unione delle due soluzioni precedenti: {1} U {2}
esempio caso (1) …
Il testo
( teoria )
x ²  6 x  8  ( x  1) … ovviamente se (x-1) < 0, per x < 1, la disequazioni non ha
alcuna soluzione.
Quindi si compone un Sistema di tipo S/N:
DS/N
x ²  6 x  8  0  (1)


x 1  0

x ²  6 x  8  ( x  1)²  (2)

e risposta
RS/N

 x  2  x  4
x 1

7

x


4
Dobbiamo quindi risolvere la (1) e la (2) col Metodo +/- e riportare le risposte su RS/N
(1)+/- Studio del C.E. del Radicale
x  2  0
D+/- 
x  4  0
( x - 2 )( x - 4 )  0 dà luogo ad un Sistema

x  2
R+/- 
x  4
e quindi la relativa risposta
Il cui grafico:
(1)+/-
Rx
2
4
-
+
-
+
+
+
… quindi riportiamo la soluzione trovata nella RS/N
+
(2)+/- Lo studio della Risolvente di 2° grado si esaurisce in una di 1° grado.
Quindi riassumendo abbiamo:
S/N
Rx
7
4
1
S
N
S
S
S
S
( spazio soluzione )
2
S
S
N
ne segue che l’unico intervallo soluzione risulta essere:
4
N
S
N
x  (1,
S
S
N
7
) … intervallo che non
4
comprende però gli estremi.
Esercizi … Teoria e TEST
Matematica  Parte III Algebra  Disequazioni Algebriche
esempio caso (2) …
Il Testo:
(2)S/N:
( teoria )
x  1  x  3 … costruiamo i due Sistemi S/N che chiameremo (1)S/N e
(1)S/N
… se (x – 3) < 0 , cioè negativo, allora essendo il Radicale positivo o eguale a zero, basta
e avanza che il suo radicando ( x – 1 ) > 0, quindi
x 1  0
DS/N 
x  3  0
e relativa risposta
x  1
RS/N 
x  3
E quindi il grafico S/N … che in questo caso dà per soluzione proprio la Risposta R, cioè
l’intervallo x  1;3 .
(2)S/N
… se invece (x – 3)  0, cioè positivo o nullo, allora il Radicale deve ( per richiesta della
Disequazione ) superare (x – 3 ) , al variare di x in R; quindi
 x  1  ( x  3)²
DS/N 
 x3 0
e relativa risposta
2  x  5
RS/N 
 x3
…. La prima linea è una disequazioni di 2° grado che risolviamo col Metodo +/- e ne
abbiamo riportato il risultato.
Adesso col Grafico S/N ricaviamo la soluzione x  3;5
Possiamo concludere con l’Unione delle due Soluzioni nello studio Complementare:
{ (1)S/N } U { (2)S/N }  1;3  3;5 che dà luogo all’unico intervallo [ 1 ; 5 )
Esercizi … Teoria e TEST
Matematica  Parte III Algebra  Disequazioni Algebriche
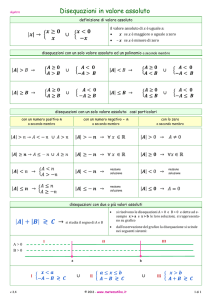
Disequazione con Valore Assoluto
( sommario )
Si possono verificare due tipologie di casi ( omettendo il caso di “=” ):
(1) A( X )  B( X ) ( esempio 1 )
(2) A( X )  B( X ) ( esempio 2 )
(1A)
DS/N
 A( x)  0

B( x)  0  (*)
 A( x)  B( x)

RS/N





(*) perché il |A(x)| non può essere ( per definizione ) < di 0
(1B)
DS/N
 A( x)  0

B( x)  0  (*)
  A( x)  B( x)

RS/N





Nel Secondo Caso è più semplice perché se B(x) è < 0 la Disequazione risulta sempre
verificata, quindi omettiamo di scriverla nella Domanda DS/N :
(2A)
 A( x)  0
DS/N 
 A( x)  B( x)

RS/N 

 A( x)  0
DS/N 
 A( x)  B( x)

RS/N 

(2B)
In definitive la Soluzione di ogni Disequazione sarà l’Unione Insiemistica delle relative
soluzione, quindi Sol. = {A}U{B}.
esempio Valore Assoluto (1) …
( teoria )
testo: |x² - 4| < x – 1
(1A)
 ( x²  4)  0
 ( x ²  4)  0


 x 1  0   x 1  0
 x²  4  x  1  x²  x  3  0



 x  2  x  2
DS/N

RS/N 
x 1
1  13
1  13
 2  x 
2
Ovviamente le linee 1 e 3 sono state risolte col Metodo +/-.
(1B)
DS/N
 ( x ²  4)  0
 ( x ²  4)  0


  x 1  0
 x 1  0
 x ²  4  x  1  x ²  x  5  0


RS/N

2 x  2


x 1


 1  21
 1  21
x
 x 
2
2
E relativi Grafici S/N:
(1A)S/N
Rx
1  13
2
2
S
N
N
N
N
N
1
N
N
S
1  13
2
2
N
S
S
S
S
S
( spazio soluzione )
S
S
N
(1B)S/N
Rx
 1  21
2
N
N
S
2
N
N
N
Quindi la Soluzione è = (
 1  21
2
1
S
N
N
S
S
N
2
S
S
S
( spazio soluzione )
N
S
S
 1  21
1  13
 1  21 1  13
;2 ) U [2 ;
) e quindi (
;
)
2
2
2
2
Esercizi … Teoria e TEST
Matematica  Parte III Algebra  Disequazioni Algebriche
esempio Valore Assoluto (2) …
( teoria )
testo: |x² - 5x -6| > x + 2
(1A)
DS/N
 ( x ²  5 x  6)  0
( x  1)( x  6)  0




( x ²  5 x  6)  x  2
 x²  6 x  8  0



x  1  x  6


RS/N 
 6  78
6  78
x

2
 2
Ovviamente le due linee sono state risolte col Metodo +/-.
(1B)
DS/N
 ( x ²  5 x  6)  0
( x  1)( x  6)  0


RS/N


 x ²  5 x  6  x  2
 x²  4 x  4  0


1  x  6



x  2  2 2  x  2  2 2

E relativi Grafici S/N:
(1A)S/N
Rx
6  78
2
S
S
( spazio soluzione )
1
S
N
6  78
2
6
N
N
S
N
S
S
( spazio soluzione )
(1B)S/N
Rx
22 2
1
N
N
S
N
22 2
S
S
( spazio soluzione )
Quindi la Soluzione è = (   ;
6
S
N
N
N
6  78
6  78
)U(
;) U (22 2 ;2 2 2)
2
2
Esercizi … Teoria e TEST
Matematica  Parte III Algebra  Disequazioni Algebriche
Ulteriori Approfondimenti
… dal sito www.ripmat.it ( completo e approfondito )
Questo scritto è stato studiato e prodotto dà Girgenti Giorgio, Insegnante di Matematica dell’ITIS “G.
Marconi” di Domodossola. E’ consentito l’uso per scopi didattici citandone le fonti. Si ringrazia Luciano Pirri per
aver fornito ulteriori esercizi, teoria e test. Si ringrazia anche l’ottimo estensore del Sito RipMat del M.P.I