Universita' degli Studi di Roma “La Sapienza”
Corso di Laurea in Ingegneria Gestionale
Corso di FISICA (M-Z)- Prof G. Zollo
Appello del 06.07.2004
Prova scritta
I parte: Meccanica
Esercizi
1) Un punto materiale di massa m=0.5 kg e' sospeso
p
mediante due fili di uguale lunghezza l=30 cm,
l l q
m
l
inestensibili e di massa trascurabile al soffitto di un
carrello. I due fili sono vincolati nei punti p e q del
soffitto distanti l. Supponendo che il carrello scenda
lungo un piano inclinato di angolo α=45° con
α
accelerazione a, calcolare il minimo valore di a
affinche' entrambi i fili risultino tesi.
2) Un proiettile di massa m=5 g e velocita'
v=200
m/s
orizzontale
urta
K
M
m
anelasticamente un piattello di massa
M=200 g vincolato all'estremita' libera
di una molla di costante elastica
K=2000 N/m. Sapendo che, in seguito all'urto, la massima compressione della molla e'
∆x=5 cm, calcolare la percentuale di energia dispersa durante l'urto.
Teoria
a) Esporre gli argomenti che giustificano la introduzione della forza centrifuga nei
sistemi di riferimento non inerziali; illustrare un caso concreto.
b) Ricavare la II equazione cardinale della meccanica dei sistemi di punti materiali.
II Parte: Elettricita' e Magnetismo
(valida anche come II esonero per coloro che hanno superato il I esonero)
Esercizi
1. Una carica statica e'distribuita con densita'uniforme σ su una superficie semi-cilindrica
avente sezione semicircolare di raggio R e lunghezza infinita. Calcolare il campo
elettrostatico (modulo, direzione e verso) in un punto qualsiasi dell'asse.
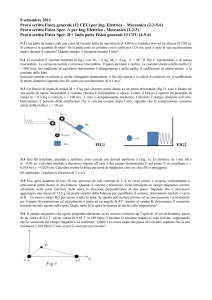
2. Sia data la spira mostrata in figura percorsa da una
corrente stazionaria di intensita'I=500 mA, calcolare il
I
O
a
campo di induzione magnetica (modulo, direzione e
verso) nel punto O indicato in figura nell'ipotesiche sia
a=3 cm e b = 7 cm.
b
Teoria
a) Definire i vettori D e P e dimostrare le relazioni di
continuita' per i vettoriD e E all'interfaccia tra due dielettrici omogenei e isotropi.
b) Definire il coefficiente di autoinduzione di un circuito e ricavare l'espressionedella
f.e.m. indotta in un solenoide di sezione circolare (raggio R) e densita'di spire n
percorso da una corrente I(t)=I0sin(ωt).
Esonerato dalla I parte-Meccanica (rispondere SI o NO)_____________
Il
sottoscritto___________________________________nato
______________________il _________matr.
N°_________________ autorizza il
trattamento dei propri dati personali ai soli fini del corso.
Data________________
a
Firma dello Studente
___________________
Universita' degli Studi di Roma “La Sapienza”
Corso di Laurea in Ingegneria Gestionale
Corso di FISICA (M-Z)- Prof G. Zollo
Appello del 06.07.2004
Soluzioni
I Parte: Meccanica
1) Qualora entrambi i fili siano tesi, nel
SNI del carrello sono presenti le forze
reali e fittizie riportate in figura e il II
principio della dinamica si scrive:
mg
T1
T2
ma
ma T 2
da cui si ottiene:
-ma T1
0 che, proiettata
sugli assi x e y fornisce:
mgcos
T 1 T 2 sin
mgsin y
0
T 1 cos
x)
0 y)
β T2
mg
α
a
x
1
a
cos
sin
m g
g
.
2
sin
cos
cos
Affinche'anche il secondo filo sia teso (oltre che il primo) deve risultare T2 >0 da cui si
ottiene:
cos
a g sin
2.93 m s 2
tan
2) La velocita'acquisita dal piattello di massa M dopo l'urtosi ottiene imponendo la
conservazione dell'energia per il piattello nel suo moto susseguente all'urto:
K
V
x 5m s .
M
Imponendo ora la conservazione della quantita'di moto per l'urtoparzialmente
T2
anelastico in questione si ha
m v M V che proiettata sull'asse fornisce:
M
m v 0 m v M V ossia v v 0
V 0 m s. Il proiettile, pertanto, si ferma
m
appena dopo l'urto. L'energia cinetica dissipata durante l'urto e', quindi
1
1
m v 20
M V 2 97.5 J che corrisponde al 97.5 % dell'energia iniziale.
Td
2
2
m v0
II Parte: Elettricita' e Magnetismo
1. La superficie semi-cilindrica puo'essere considerata come l'insiemedi fili infiniti
aventi una densita'lineare di carica pari a dl R d . Il campo elementare
generato da ciascun filo elementare e',pertanto, dato da
dE
1
2 0
R
R . Per
simmetria la componente parallela al
diametro del campo complessivo e'nulla
(ogni
filo ha il suo simmetrico) percio':
dE
d Ex i
2 si
Integrando
1
sin i .
R
0
Rdθ
θ
ottiene
R
dE
E
i
Ex
d Ex
0
i
% &
! #
2 "$
0
0
1
2 0
sin ' d
0
'
sin d
"(! #
e cioe'
.
0
2) Il campo magnetico prodotto
) da
) un) arco di spira circolare nel suo centro e'dato dalla
/ di Laplace:
/
)
integrazione
della I formula
+
B * Bz k
*
+
.0/ ) )
dl 1 r 2
2
k
,
4-
0
r'
I
1
r
2
r'
3
spira circolare, pertanto, si ha
Bz
*
./
+
,
k
4645 7
40
0
I
R
2
d
1
I
3
. Nel caso di un quarto di
R
8 9 8
1
4$5 8
0
2
I
R
. Considerando che il
campo generato dai tratti rettilinei nel punto O e' nullo abbiamo, infine
Bz
:<; 8
foglio.
0
I
1
a
=
1
b
:
> ?
1.5 10
6
T
ed e'perpendicolare ed entrante nel piano del