TRASFORMAZIONI TERMODINAMICHE
Tutte le proprietà di un gas sono perfettamente descritte da tre coordinate termodinamiche, pressione (p),
temperatura (T) e volume (V), più la quantità di materia che esso contiene (numero di moli, n)
Un gas si trova allo stato di equilibrio termodinamico quando le tre grandezze che lo caratterizzano sono
costanti nel tempo: un gas tenuto in un recipiente chiuso, isolato dall'esterno si trova allo stato di equilibrio.
Se però il recipiente che contiene il gas è chiuso da un pistone, alzando o abbassando il pistone il gas subirà
una trasformazione termodinamica, dove la sua pressione varia (aumenta o diminuisce) e solo dopo un
determinato periodo di tempo si ristabilisce l'equilibrio. Una trasformazione termodinamica è caratterizzata
perciò dal passaggio di un gas da uno stato iniziale (che chiameremo A) a uno stato finale (che
chiameremo B), attraverso una successione di stati intermedi.
Le trasformazioni termodinamiche sono alla base degli scambi di energia dovuti ai gas (e non solo
ai gas, ma noi tratteremo solo quelli dei gas): infatti, tutte le volte che un gas scambia calore (cioè
assorbe/cede calore) o quando un gas esegue un Lavoro (espansione se il gas applica il Lavoro all’esterno,
contrazione se è l’esterno ad applicare Lavoro al gas) si ha necessariamente una trasformazione
termodinamica, cioè un cambiamento di almeno una delle tre coordinate del gas. Vale anche il viceversa: se
un gas cambia almeno una delle sue coordinate (pressione, volume, temperatura) allora necessariamente c’è
uno scambio di calore o di Lavoro. In conclusione:
la trasformazione termodinamica è l’unico mezzo che un gas ha per scambiare energia
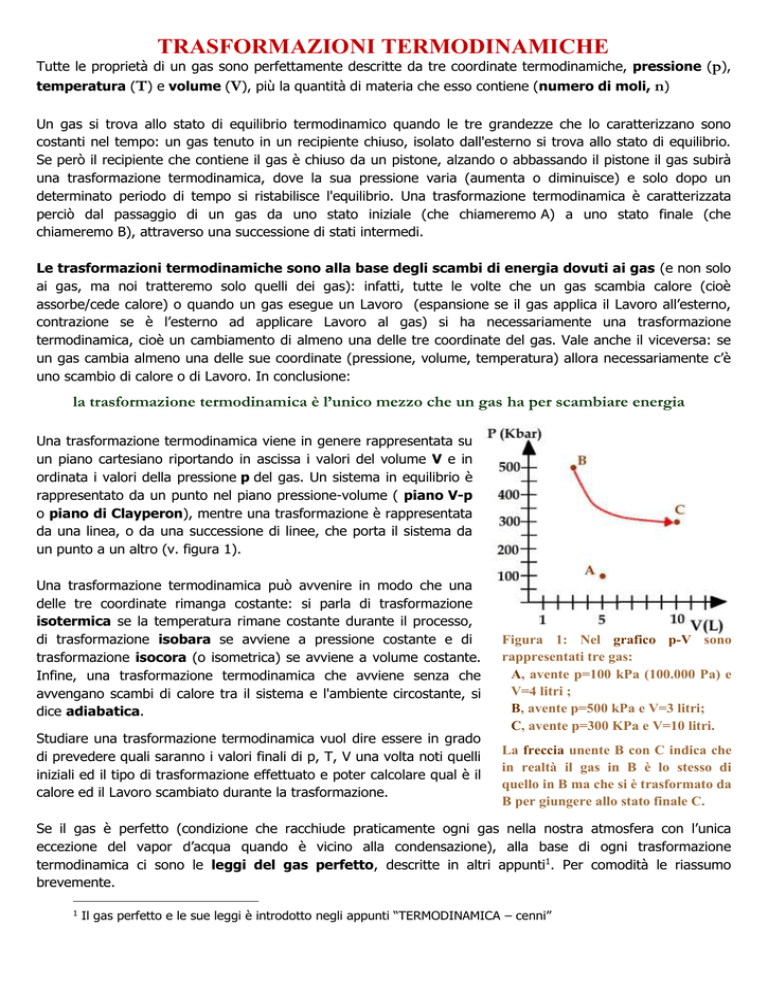
Una trasformazione termodinamica viene in genere rappresentata su
un piano cartesiano riportando in ascissa i valori del volume V e in
ordinata i valori della pressione p del gas. Un sistema in equilibrio è
rappresentato da un punto nel piano pressione-volume ( piano V-p
o piano di Clayperon), mentre una trasformazione è rappresentata
da una linea, o da una successione di linee, che porta il sistema da
un punto a un altro (v. figura 1).
Una trasformazione termodinamica può avvenire in modo che una
delle tre coordinate rimanga costante: si parla di trasformazione
isotermica se la temperatura rimane costante durante il processo,
di trasformazione isobara se avviene a pressione costante e di
trasformazione isocora (o isometrica) se avviene a volume costante.
Infine, una trasformazione termodinamica che avviene senza che
avvengano scambi di calore tra il sistema e l'ambiente circostante, si
dice adiabatica.
Studiare una trasformazione termodinamica vuol dire essere in grado
di prevedere quali saranno i valori finali di p, T, V una volta noti quelli
iniziali ed il tipo di trasformazione effettuato e poter calcolare qual è il
calore ed il Lavoro scambiato durante la trasformazione.
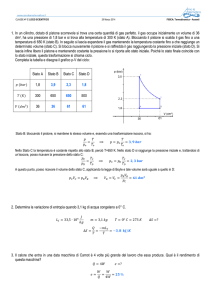
Figura 1: Nel grafico p-V sono
rappresentati tre gas:
A, avente p=100 kPa (100.000 Pa) e
V=4 litri ;
B, avente p=500 kPa e V=3 litri;
C, avente p=300 KPa e V=10 litri.
La freccia unente B con C indica che
in realtà il gas in B è lo stesso di
quello in B ma che si è trasformato da
B per giungere allo stato finale C.
Se il gas è perfetto (condizione che racchiude praticamente ogni gas nella nostra atmosfera con l’unica
eccezione del vapor d’acqua quando è vicino alla condensazione), alla base di ogni trasformazione
termodinamica ci sono le leggi del gas perfetto, descritte in altri appunti1. Per comodità le riassumo
brevemente.
1
Il gas perfetto e le sue leggi è introdotto negli appunti “TERMODINAMICA – cenni”
Leggi del gas perfetto
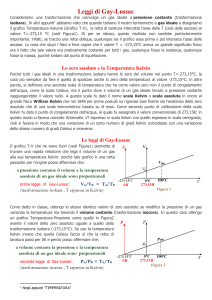
in una trasformazione a temperatura costante (isoterma), il prodotto pressione x
volume rimane costante (Legge di Boyle-Mariotte)
In formule: PV = cost
(T cost.)
in una trasformazione a pressione costante (isobara) la pressione è proporzionale alla
temperatura in Kelvin (1° Legge di Gay-Lussac)
In formule: p1/T1 = p2/T2 (V cost) , con la temperatura espressa in Kelvin.
in una trasformazione a volume costante (isocora) la pressione è proporzionale alla
temperature in Kelvin (2° Legge di Gay-Lussac)
In formule: V1/T1 = V2/T2 (p cost) , con la temperatura espressa in Kelvin.
fissata temperatura e volume , la pressione è direttamente proporzionale al numero di
moli
In formule: p n (p e V cost e di conseguenza anche T cost)
Tutte queste quattro leggi sono raggruppabili in un’unica equazione che lega insieme p,V,T,n: tale equazione
si chiama equazione di stato dei gas perfetti:
equazione di stato del gas perfetto
pV = nRT , T in kelvin
R è la costante dei gas perfetti, il cui valore risulta essere [ R = 8,314472 (pressione in
Pascal, volume in m3) o alternativamente R=0,08205784 (pressione in atm, volume in litri=dm3) ]
Adesso risolveremo alcuni semplici problemi per impratichirci delle proprietà essenziali delle trasformazioni
termodinamiche: ci concentreremo soltanto su come cambiano le coordinate di un gas p , V , T senza
preoccuparci degli scambi di energia: quest’ultimi saranno accennati in seguito, quando ci saremo impratichiti
dei concetti fondamentali delle trasformazioni termodinamiche.
PROBLEMI INTRODUTTIVI
È interessante iniziare a studiare delle trasformazioni di stato particolari, dove si mantiene costante, durante la
trasformazione, una delle tre variabili di stato.
Trasformazione isocora o isometrica (V = costante)
Si ha quando durante la trasformazione del gas tra due stati di equilibrio, si mantiene costante il volume. Per
una trasformazione isocora si applica la 1° legge di Gay-Lussac: p1/T1 = p2/T2
Supponiamo di avere un gas chiuso dentro un recipiente sigillato (a volume costante di 5 litri) alla pressione
p=200 kPa (1kPa = 1000 Pa) e alla temperatura T=20°C; se lo riscaldo alla temperatura di 300 °C , quale
sarà la sua pressione?
Soluz: Applico la 1° legge di Gay-Lussac: p1/T1 = p2/T2 ;
p1=200kPa , T1=20°C , T2=300°C.
Poiché la legge di Gay-Lussac è scritta per la temperatura in
Kelvin, trasformo i gradi Celsius in Kelvin. TKELVIN = TCELSIUS +
273,15 , che arrotondo per comodità a TKELVIN = TCELSIUS +
273,15
T1 = 20+273 = 293K ; T2 = 300+273 = 573K
p1/T1 = p2/T2 200kPa/293 = p2/573 p2=391,1kPa
Tale relazione, nel piano (V - p) è rappresentata da una retta
parallela all’asse delle pressioni (asse verticale).
Figura 1: trasformazione isocora. Il gas passa dal punto A1 al
punto A2 scaldandosi ed aumentando la sua pressione.
Trasformazione isobara (p = costante) Si ha quando durante la trasformazione del gas tra due stati di
equilibrio, si mantiene costante la pressione. La trasformazione segue la legge V1/T1 = V2/T2.
Supponiamo di avere un gas aperto all’aria, soggetto perciò alla
pressione costante di circa 100.000 Pa (100 kPa); supponiamo che
alla temperatura di 200°C esso occupi un volume di 8 litri. Se
raffreddo il gas portandolo alla temperatura di -15°C, quale sarà il
suo volume finale?
Soluz: Applico la 2° legge di Gay-Lussac: V1/T1 = V2/T2 ;
V1=8 litri , T1=18°C , T2=-15°C.
Poiché la legge di Gay-Lussac è scritta per la temperatura in
Kelvin, trasformo i gradi Celsius in Kelvin.
TKELVIN = TCELSIUS + 273,15 , che arrotondo per comodità a
TKELVIN = TCELSIUS + 273
T1 = 200+273 = 473K ; T2 = -15+273 = 258K
V1/T1 = V2/T2 8litri/473 = V2/258 V2=4,36 litri
Figura
2:
trasformazione
isobara. Il gas passa dal punto
A1 al punto A2 raffreddandosi
e diminuendo il suo volume.
Tale relazione, nel piano (V - p) è rappresentata da una retta parallela all’asse dei Volumi (asse orizzontale).
Trasformazione isoterma (T = costante) Si ha quando durante la trasformazione del gas tra due stati di
equilibrio, si mantiene costante la temperatura. E’ tipica di trasformazioni lente che hanno il tempo di
scambiare calore con l’esterno per mantenere sempre costante la loro temperatura. La compressione o la
dilatazione del gas dentro una siringa è una tipica trasformazione isoterma se lo stantuffo è mosso
lentamente.
Per una trasformazione isoterma vale la legge di Boyle-Mariotte: pV = costante = nRT
All’aumentare del volume diminuisce la pressione e viceversa al diminuire del volume aumenta la pressione, in
modo che il prodotto p⋅V rimanga sempre lo stesso.
Supponiamo che un gas occupi un volume di 10 litri alla pressione
atmosferica (100 kPa): esso viene compresso lentamente fino a giungere al
volume di 2 litri: qual è la sua pressione se la trasformazione è stata
isoterma?
Soluz: Applico la legge di Boyle-Mariotte: pV = cost; p1=100kPa ,
V1=10 litri ; V2=2 litri Non ho bisogno di alcuna conversione: applico
subito la legge:
p1V1 = p2V2 100kPa10L = p22L p2=500kPa
Tale relazione, nel piano (V - p) è rappresentata da una iperbole
equilatera: inversamente, se un gas si trasforma in modo da seguire
un’iperbole equilatera nel grafico p-V allora la sua temperatura è
rimasta costante.
Figura
3:
trasformazione
isoterma. Il gas passa dal punto
A1 al punto A2 essendo
compresso ed aumentando così
la sua presione.
Trasformazione generica (tratto da “Fisica”, di J. Walker)
Adesso confideremo una trasformazione generica, cioè che non rientra in
nessuna delle tre categorie considerate. Per studiarla applicheremo
perciò l’equazione più generale: quella di stato dei gas perfetti.
Considera di avere una bombola d’aria compressa che contiene 0.5 m3 di
aria a temperatura 285 K e pressione 850 kPa. Calcola che volume
occuperebbe quest’aria se fosse rilasciata nell’atmosfera dove la
pressione è 101 kPa e la temperature di 303 K.
Soluz: Lo stato iniziale del gas viene descritto attraverso la
pressione, il volume e la temperatura. Della situazione finale
conosciamo, invece, la pressione e la temperatura. Non essendo
specificato il tipo di trasformazione, l’unica equazione che si è
legittimati ad usare è quella dei gas perfetti: pV=nRT
Figura
4:
trasformazione
generica da A1 ad A2.
Essendo R una costante nota, i parametri che non si conoscono sono
il volume finale e il numero di moli n.
Calcolo di n: utilizzando l’equazione dei gas perfetti, applicata alle informazioni sulle condizioni
iniziali, è possibile ottenere il numero di moli: n = p1V1/RT1
Poiché il numero n è l’unica quantità che rimane invariata prima e dopo (la quantità di gas non si
crea né si distrugge), si può trovare il volume attraverso la relazione: V2 = nRT2/ P2
Ottenendo il seguente risultato: V2 =4,5 m3
Dato che il tipo di trasformazione non è specificato, non sappiamo come unire i due punti A1 e A2
nel piano V-p: la possibile trasformazione potrebbe essere quella tratteggiata ma anche qualsiasi
altra unente i due punti.
PROBLEMI PERFETTI
Adesso ci eserciteremo a risolvere alcuni semplici problemi riguardanti le trasformazioni dei gas perfetti.
Problema1: la trasformazione isoterma (tratto da “Lineamenti di Fisica”, di P. Alberico)
Un gas perfetto, alla pressione di 3 atmosfere, occupa un volume di 30 dm3. Di quanto si deve espandere, a
temperatura costante, per portarsi alla pressione normale di 1 atmosfera?
Soluz: Dato che la trasformazione avviene a temperatura costante (isoterma) è possibile
utilizzare la legge di Boyle-Mariotte: p1V1 = p2V2
Di questa relazione si conoscono la pressione ed il volume iniziali e, anche, la pressione finale.
Utilizzando direttamente questa relazione è possibile trovare il valore del volume finale da cui poi
dedurre di quanto si è dovuto espandere. In particolare:
p1V1 = p2V2 3atm30dm3 = 1atmV2 V2 = 90dm3
Nota sulle unita di misura: nel fare i calcoli non sono stati necessari cambiamenti di unità di misura
essendo tutte le grandezze espresse son le solite unità di misura.
Problema2: le due trasformazioni. Una data massa di gas che a 0°C occupa un volume di 10 litri ed ha una
pressione di 5 atm viene riscaldato a 150 °C. Calcolare: a) il volume occupato dal gas se si mantiene costante
la pressione; b) la pressione esercitata dal gas se si mantiene costante il volume
Soluz:
a) Applichiamo la prima legge di Gay Lussac: V1/T1= V2/T2 dopo aver operato le opportune
conversioni della temperatura:
T1 = 0°C = 273 K e T2 = 150 + 273 =423 K
Sostituiamo i valori noti nella relazione V1/T1= V2/T2
10L/273K = V2/423K V2 = 15.5 L
b) Applichiamo la seconda legge di Gay Lussac: p1/T1= p2/T2
5atm/273K = p2/423K p2 = 7,75 atm
Problema3: isobara. Una data massa di gas occupa a 20 °C il volume di 0,05 m3. Calcolare a quale
temperatura espressa in gradi Kelvin occorre portare il gas affinché il volume diventi 100 L a pressione
costante.
Soluz:
Applichiamo la prima legge di Gay Lussac: V1/T1= V2/T2 , dopo aver operato le opportune
conversioni della temperatura e del volume: T1 = 20 + 273 = 293 K
0,05 m3 = 50 dm3 = 50 L
Sostituiamo i valori noti nella relazione V1/T1= V2/T2
50L/293K = 100L/T2 T2 = 586 K = (586-273) = 313°C
Problema4: trasformazione generica. Alla temperatura di 127 °C un gas contenuto in un recipiente di 2 L
esercita una pressione di 3 atm (300.000Pa). Calcolare quale volume occupa il gas alla pressione d 1 atm
(100.000 Pa) e alla temperatura di 0 °C
Soluz: Applichiamo la legge di stato dei gas: pV=nRT
Per conoscere il volume finale (V2) devo per prima cosa calcolare il numero di moli n e poi
calcolare V2.
Calcolo di n: utilizzando l’equazione dei gas perfetti, applicata alle informazioni sulle condizioni
iniziali, è possibile ottenere il numero di moli: n = p1V1/RT1 n=0,18 moli
Poiché il numero n è l’unica quantità che rimane invariata prima e dopo (la quantità di gas non si
crea né si distrugge), si può trovare il volume attraverso la relazione: V2 = nRT2/ P2
Tutte le temperature devono essere espresse in Kelvin: T1=127+273=400K ; T2=0+273=273K.
Ottenendo il seguente risultato: V2 =4,085 m3
Problema5: i disegnini. Disegna sul grafico V-p queste trasformazioni:
a) Isoterma da p1=400kPa , V1=5l V2=10l (p2=200kPa)
b) Isobara con p1=p2=100kpa; V1=5L V2=10L
c) Isocora con V1=V2=3L ; p1=500kPa p2=200kPa
Soluz: i grafici sono mostrati sotto
Problemi estratti dal sito: “http://www.chimicamo.org/stechiometria/esercizi-svolti-sui-gas.html”
Potete trovare altri problemi svolti all’indirizzo” http://www.uniroma2.it/didattica/ChimicaMedica/deposito/es._gas.pdf”