Esame Scritto, Modulo di Fisica, Corso di Chimica e Fisica Generali, per Biotecnologie
24 Luglio 2013
Il tempo a disposizione è di tre ore. E’ ammesso l’uso di calcolatrici. Non è ammesso l’uso di appunti, libri, computer,
telefoni, altri dispositivi di comunicazione. Un libro di testo è a disposizione per consultazione. Costanti utili:
accelerazione di gravità 9.81 m/s2 , densità dell’acqua 103 Kg/m3 , costante di Coulomb κ = 8.99 · 109 Nm2 C−2 Si
raccomanda di spiegare in modo conciso ma chiaro il procedimento seguito: risposte del tutto prive di giustificazione
non saranno considerate valide anche se corrette. Ogni domanda sarà valutata fino a 6 punti.
Problema 1 (6 punti)
Una scala lunga L = 30 m è appoggiata alla parete di un edificio con una inclinazione di α = 40◦ con la parete.
Dalla sua sommità cade (verticalmente!) un oggetto. Dopo quanto tempo e con che velocità l’oggetto tocca terra,
trascurando ogni attrito?
Problema 2 (12 punti)
Un punto materiale oscilla in una ciotola di forma semisferica di raggio 4 cm, attorno al fondo della ciotola (posizione
di equilibrio), raggiungendo un’altezza dal fondo pari a 1 cm.
• Trascurando l’attrito, quanto vale la velocità raggiunta dal punto sul fondo della ciotola?
• Se sostituiamo il punto materiale con una pallina che rotola senza strisciare, cosa cambia? quanto vale la velocità
dalla pallina sul fondo?
Problema 3 (6 punti)
Una situazione classica dei fumetti è quella del personaggio che, inseguito da uno sciame di api, si rifugia in fondo ad un
laghetto respirando attraverso un cannello. Tuttavia nel mondo reale i polmoni non funzionano se il differenziale ∆P
fra pressione interna (in questo caso, quella atmosferica) e pressione esterna eccede 0.050 Bar, ovvero se ∆P > 5000
Pa. Stimare fino a quale profondità si riesce a respirare aiutandosi con un cannello.
Problema 4 (12 punti)
Tre cariche, q1 = 4 × 10−6 C, q2 = −2 × 10−6 C, and q3 = 5 × 10−6 C, sono piazzate agli angoli di un quadrato di lato
d = 0.30 m. Le cariche q2 e q3 sono sugli angoli adiacenti al quarto angolo, la carica q1 sull’angolo opposto al quarto
angolo.
• Quanto vale il potenziale elettrico generato dalle tre cariche nel quarto angolo?
• Quanto vale in modulo il campo elettrico generato dalle tre cariche nel quarto angolo?
1
Soluzioni
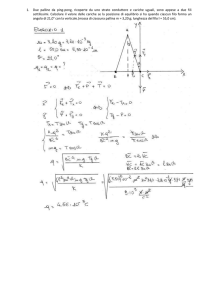
Problema 1
Il punto più alto della scala si trova a h = L cos 40◦ da terra (notare che l’angolo è di 40◦ fra scala e parete, non
p fra
2h/g
scala e suolo). Un oggetto
che
cade
da
altezza
h
con
moto
uniformemente
accelerato
arriverà
a
terra
dopo
t
=
√
con velocità v = gt = 2hg. Inserendo i valori si ottiene h = 22.98 m, t = 2.16 s, v = 21.23 m/s.
Problema 2
• Nel fondo della ciotola, l’energia meccanica è puramente cinetica: possiamo scegliere infatti lo zero dell’energia
potenziale nel fondo della ciotola, e vale Ek = mv 2 /2; nel punto più alto raggiunto dal punto materiale, l’energia
meccanica è puramente potenziale e vale Ei = mgh,
√ dove h = 0.01 m. Dato che l’energia meccanica si conserva,
si ha Ek = Ei , ovvero mv 2 /2 = mgh, ovvero v = 2gh = 0.44 m/s. Notare che la forma della ciotola non entra
da nessuna parte!
• L’energia cinetica di una pallina è la somma dell’energia cinetica di traslazione: Et = mv 2 /2, dove v è la
velocità del centro di massa, e dell’energia cinetica di rotazione attorno al centro di massa: Er = Iω 2 /2, dove
ω è la velocità angolare di rotazione attorno ad un asse passante per il centro di massa, I = 2mr2 /5 è il
momento d’inerzia di una sfera di raggio r. Se la pallina rotola senza strisciare, vale la relazione v = ωr. Da
qui, Er = mv 2 /5, e l’energia cinetica totale della pallina Ek = Et + Er = 7mv 2 /10. Come in precedenza, la
conservazione dell’energia ci dice che Ek = mgh, dove h è la differenza di quota del centro di massa della pallina
fra il punto più alto raggiunto (pallina che sip
ferma e inverte il moto) e quello più basso (pallina in fondo alla
ciotola). Assumendo ancora h = 0.01 m, v = 10gh/7 = 0.37 m/s. La velocità della pallina è quindi inferiore a
quella di un punto materiale, a parità di dislivello.
Problema 3
Non si riesce più a respirare quando la pressione idrostatica, che a profondità h vale P = ρgh per un liquido di densità
ρ eccede P0 = 0.050 Bar, ovvero quando h > P0 /(ρg) = 5000 Pa /1000 Kg m3 /9.81 m/s2 = 0.51 m.
Problema 4
• Il potenziale elettrico V è la somma dei potenziali generati dalle tre cariche: V = κ(q1 /r1 + q√2 /r2 + q3 /r3 ),
dove r1 , r2 , r3 sono le distanze√fra il quarto vertice e le tre cariche. Dato che r2 = r3 = d, r1 = 2d, si ottiene
V = 8.99 × 109 · (−2 + 5 + 4/ 2) × 10−6 /0.3 Volt ovvero V = 175000 Volt circa.
• Il campo elettrico è la somma vettoriale dei campi elettrici generati dalle tre √
cariche. Lungo la direzione
2-4, solo
√
la carica 2 e la carica 1 producono un campo elettrico : Ex = κ(q2 /r22 + q1 2/(2r12 )) (il fattore 2/2 è dovuto
alla selezione di una componente del campo).
Lungo la direzione 3-4, solo la carica 3√e la carica 1 producono
√
un campo elettrico : Ey = κ(q3 /r32 + q1 2/(2r12 )). Inseriamo r2 = r3 = d, r1 = 2d e i fattori numerici:
−6
2
5
9
−6
2
Ex = 8.99 × 109 · (−2
q+ 4/4) × 10 /0.3 V/m = −10 V/m; Ey = 8.99 × 10 · (5 + 4/4) × 10 /0.3 V/m
= 6 × 105 V/m; E =
Ex2 + Ey2 = 6.08 × 105 V/m.
2