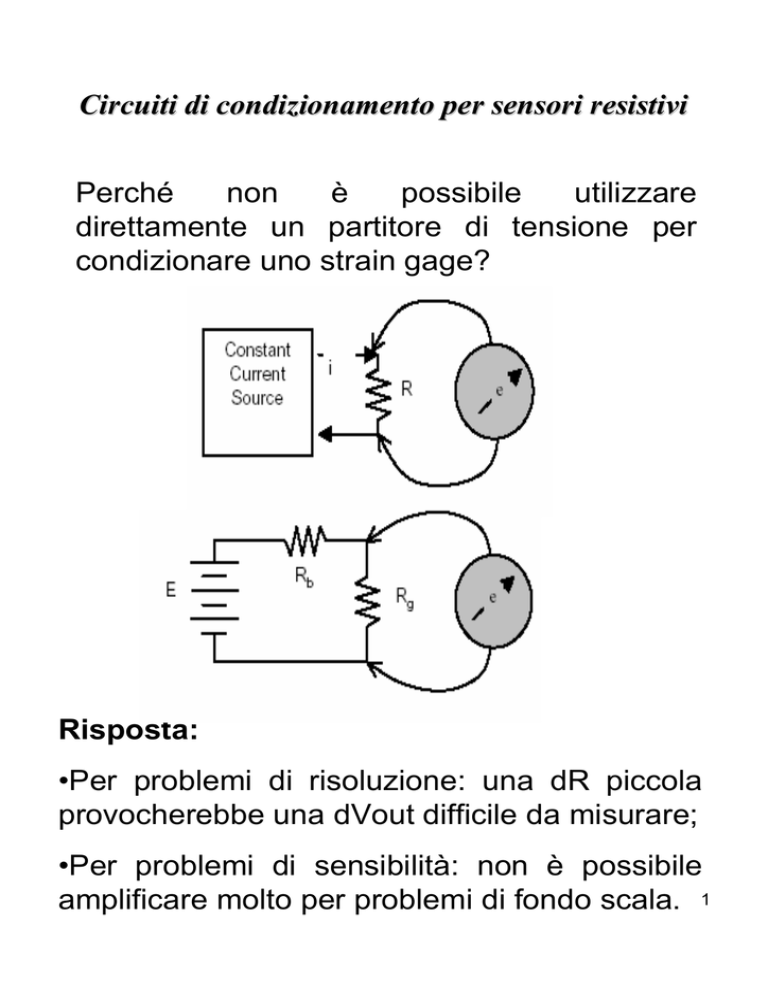
Circuiti di condizionamento per sensori resistivi
Perché
non
è
possibile
utilizzare
direttamente un partitore di tensione per
condizionare uno strain gage?
Risposta:
•Per problemi di risoluzione: una dR piccola
provocherebbe una dVout difficile da misurare;
•Per problemi di sensibilità: non è possibile
amplificare molto per problemi di fondo scala. 1
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone
In particolare una variazione di resistenza è
misurabile utilizzando un ponte di
Wheatstone, in cui uno o più lati sono
elementi variabili.
C
R2
R1
V
- Vo +
A
R4
B
R3
D
2
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone
Metodo di confronto: Un elemento incognito viene
direttamente confrontato con uno campione tramite organi
di regolazione e rivelatori della condizione di equilibrio
C
R2
R1
V
- Vo +
A
R4
B
R3
D
Metodo di zero: E’ possibile
effettuare la stima di una delle
quattro resistenze del ponte,
verificando
la
condizione
d’equilibrio V0 = 0
La condizione d’equilibrio (Vo=0) si ha per:
R1 R2
⎛ R3
R4 ⎞
=
⎟⎟V
V0 = ⎜⎜
−
R 4 R3
⎝ R2 + R3 R1 + R4 ⎠
da questa, noti i valori di R1, R2 ed R4 si ricava R3.
3
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone a bilanciamento
C
R2
R1
V
- Vo +
A
R4
B
RR33=R0(1+x)
D
Es. Variando uno dei lati del ponte (ad es.
R2) è possibile ottenere l’equilibrio
(V0=0). In queste condizioni è possibile
stimare il valore di R3 mediante la
relazione:
R4
R3 =
R2
R1
4
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: effetto delle RW
C
R2
R1
V
- Vo +
A
Rw
B
R4
R3
D
Rw
R3 + 2RW
R4
=
R2
R1
R4
R3 =
R2 − 2RW
R1
L’effetto delle resistenze dei conduttori rende
poco affidabile la stima di R3 a causa
5
dell’aleatorietà delle RW.
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: effetto delle RW,
connessione a 3 fili
C
R2
R1
V
Rw
- Vo +
A
B
R4
Rw
Rw
R3
D
R3 + RW
R4
=
R2 + RW
R1
R3 + RW
R4
(R2 + RW )
=
R1
se R1 = R4
si ha : R3 = R2
6
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone a
bilanciamento automatico
C
R2
R1
V
- Vo +
A
R4
B
RR3 3=R0(1+x)
D
•Da un punto di vista operativo esistono
diverse configurazioni che permettono
il bilanciamento automatico del ponte
(mediante
soluzioni
mecaniche
o
elettriche). In questo caso la stima del
valore di R3 è ottenuta in maniera indiretta
valutando
l’azione necessaria per
bilanciare il ponte.
•Queste soluzioni comportano tempi di
misura elevati.
7
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone a deflessione
Invece di misurare l’entità dell’azione necessaria a ristabilire
l’equilibrio del ponte è possibile ottenere un segnale elettrico
funzione della variazione degli elementi del ponte.
C
R2
R1
V
- Vo +
A
R4
B
R3=R0(1+x)
D
⎛ R3
R4 ⎞
⎟⎟V
V0 = ⎜⎜
−
⎝ R2 + R3 R1 + R4 ⎠
⎛ R0 (1 + x )
R4 ⎞
⎟⎟V
Vo = ⎜⎜
−
⎝ R2 + R0 (1 + x ) R1 + R4 ⎠
1 ⎞
⎛ 1+ x
Vo = ⎜
−
⎟V
⎝ k +1+ x k +1⎠
kx
V
Vo =
(k +1)(k +1+ x)
R1 R2
k= =
R4 R0
8
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: linerità
C
R2
R1
V
- Vo +
A
R4
B
R3=R0(1+x)
D
(1)
kx
V
Vo =
(k +1)(k +1+ x)
(2)
R1 R2
k= =
R4 R0
•Si osservi che per x=0 si ha V0=0: infatti per x=0 la
condizione (2) diventa quella d’equilibrio del ponte.
L’uscita è lineare per x<<k+1 !!!!
⎛ kx ⎞
⎟V
V0 ≅ ⎜
2
⎜ ( k + 1) ⎟
⎝
⎠
9
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: sensibilità
Sensibilità rispetto a x
Supponiamo di partire da una condizione di equilibrio (x=0);
una variazione pari a x produrrà una variazione di R3 pari a
R0(1+x)-R0=R0x e quindi una tensione V0:
DV0
V0
kV
1
S=
=
=
DR3 xR0 R0 (k + 1)(k + 1 + x )
S
dS
= 0 → k2 = 1+ x
dk
x= 0.01
k
10
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: progettazione
Le due condizioni:
x << 1 + k
(1)
k = 1+ x
(2)
2
sono molto importanti ai fini del dimensionamento
degli elementi del ponte.
(
x = εG = 500010
−6
)(2.0) = 0.01
In questo caso le condizioni (1) e (2) sono verificate!!!
11
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: progettazione
Le due condizioni:
x << 1 + k
(1)
k 2 = 1+ x
(2)
sono molto importanti ai fini del dimensionamento
degli elementi del ponte.
PT100
x = αDT
α = 0.00385
se DT = 200°C
si ha : x = 0.8
dalla (2) k = 1.3
la (1) 0.8 << 2.3 NON è pienamenteverificata!!
12
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: progettazione
(
x = εG = 5000 ⋅10
−6
)(2.0) = 0.01
In questo caso le condizioni (1) e (2) sono verificate!!!
•Si osservi comunque che:
R = R0 (1 + x ) = 120 (1 + 0.01) = 121 .2Ω
DR = R − R0 = 1.2Ω
5V * 0.01
V0 ≈
= 12 .5mV
4
E’ necessario utilizzare uno stadio di
amplificazione!!
13
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: progettazione
C
R2
R1
V
- Vo +
A
R4
B
R3=R0(1+x)
D
Anche volendo aumentare la tensione di
alimentazione del ponte bisogna considerare la
massima corrente che può scorrere sul
sensore.
Ad esempio nel caso di uno SG, sia il valore
della corrente massima pari a 30mA. Si ha:
eex = 2 * R0 * 30 * 10−3 = 7.2 V
7.2 * 0.01
V0 =
= 18mV
4
In ogni caso il valore della tensione in uscita dal
trasduttore è molto piccola ed è necessario ricorrere
a degli amplificatori.
14
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: progettazione
Il limite inferiore della tensione che può essere
misurata (e quindi della resistenza) dipende dal
rumore termico associato alla resistenza stessa.
Nel caso dello strain gage in esame, ai suoi
capi si realizzerà una tensione di rumore il
cui valore quadratico medio vale:
Per l’esempio in esame si ricava:
Enoise,rms = 4kTRΔf
k = 1.38 ⋅ 10− 23 J / k
T = 300K , Δf = 100000Hz
Enoise,rms = 0.45μV
15
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: progettazione
Es. si vuole misurare una temperatura in un
range [-10°C, 50°C]. Si vuole che la
tensione di uscita V0 vari tra -1V e 5V e che
l’accuratezza sia pari a:
0.5% lettura + 0.2%FS.
α = 0.4% / °C
R0 0°C = 100Ω
Si utilizza un RTD con
5mW / °C
Dimensionare il ponte, e la
alimentazione. Calcolare la S
guadagno dell’amplificatore.
Vo =
Per la linearità si trova
1° condizione
kx
V
(k +1)(k +1+ x)
x << 1 + k
k=
V di
ed il
R1 R2
=
R4 R0
xmax = 0.004 * 50 = 0.2
k + 1 >> 0.2
L’incertezza relativa dovuta alla non linearità deve essere <0.005
Si ricava: x/(k+1)<<0.005
0.2/(k+1)<<0.005
da cui k>39. Scegliendo k=39 verifico anche la 1° condizione.
16
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: progettazione
range [-10°C, 50°C];
V0 [-1V e 5V]
accuratezza sia pari a:0.5% lettura + 0.2%FS.
RTD con α = 0.4% / °C, R0 0°C = 100Ω, 5mW / °C
Dimensionare il ponte, e la V di alimentazione. Calcolare
la S ed il guadagno dell’amplificatore.
k=39
k=
R1 R2
=
R4 R0
Fissando R1=R2 e R4=R0 si ottiene
R1=R2=3900Ω e R4=R0=100 Ω
La V si fissa compatibilmente con l’autoriscaldamento:
⎛ V
⎞
2
⎜
⎟
P = R3I = R3 ⎜
⎟
⎝ R 2 + R3 ⎠
2
R max = 120 Ω
3
massimo riscaldame nto consentito 0.2% 50 °C = 0.1°C
da cui la potenza dissipata max vale 0.5mW
2
V
⎛
⎞
120 ⎜
⎟ < 0.5mW
3900
+
120
⎝
⎠
V < 8 .2V
V = 8V
17
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: progettazione
range [-10°C, 50°C];
V0 [-1V e 5V]
accuratezza sia pari a:0.5% lettura + 0.2%FS.
RTD con α = 0.4% / °C, R0 0°C = 100Ω, 5mW / °C
Dimensionare il ponte, e la V di alimentazione. Calcolare la S ed
il guadagno dell’amplificatore.
k=39
La sensibilità:
S=
kVα
(k + 1)
2
= 0.78mV / °C
Vomax = 0.78 * 50 = 39mV
G AMPL = 5 / 39e − 3 = 128.2
18
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone a corrente costante
C
I1
I
R1
R2
V1
V2
A
I2
B
R4
R3=R0(1+x)
D
R2 + R3
I1 = I
R1 + R2 + R3 + R4
R1 + R4
I2 = I
R1 + R2 + R3 + R4
Vo = V2 −V1 = R3I2 − R4 I1
R3 ( R1 + R4 )
R4 ( R2 + R3 )
Vo
=
−
I R1 + R2 + R3 + R4 R1 + R2 + R3 + R4
R0 R1 (1+ x) − R4 RR1 2
Vo
=
I R1 + R2 + R0 (1+ x) + R4
R1 R2
k= =
R4 R0
19
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone a corrente costante
Vo
kR0 R4 x
=
I R4 ( k +1) + R0 (1+ k + x )
Se
R4=R0
(quindi R1=R2)
R1 R2
k=
=
R4 R0
kx
V0 = IR0
2(k + 1) + x
Incremento della regione di linearità
per avere un’uscita proporzionale a x è necessario
imporre:
x<<2(k+1)
20
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone
Effetti di k
All’aumentare del valore di k cresce l’intervallo
di linearità ma diminuisce la sensitività
Ponte a tensione costante
Ponte a corrente costante
k=100
0.5
k=50
0.1
0.45
0
k=50
k=5
0.35
k=1
0.3
-0.3
k=1
0.25
-0.4
-0.5
-1
k=5
0.4
Vo/I
Vo/V
-0.1 k=10
-0.2
k=10
k=100
-0.8 -0.6 -0.4 -0.2
0
x
0.2 0.4 0.6 0.8
1
0.2
-1 -0.8 -0.6 -0.4 -0.2
0
x
0.2 0.4 0.6 0.8
21
1
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone
Misure differenziali
kR0
kR0
- Vo +
V
R0(1+x2)
R0(1+x1)
k(x1 − x2 )
Vo =V
(k +1+ x1)(k +1+ x2 )
Per x1,x2<<(k+1)
k
Vo ≈V
(x − x2)
2 1
(k +1)
22
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone
Applicazione agli strain gages
il ponte di Wheatstone, usato come
strumento di deflessione, è un dispositivo
non lineare, tuttavia se sono rispettate certe
simmetrie (e questo è il caso del ponte di
strain gage) la tensione d’uscita è una
funzione
lineare
della
variazione
di
resistenza!
23
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone
Applicazione agli strain gages: Half
R0(1-x)
R0
•Maggiore sensibilità
•Linearità
- Vo +
V
bridge
R0(1+x)
R0
2 R0 (1 + x ) − 2 R0
R0 (1 + x )
V
x
− =V
V0 = V
=V
4 R0
2
R0 (1 + x ) + R0 (1 − x ) 2
Applicazione agli strain gages: Full
R0(1+x)
R0(1-x)
V0 = Vx
- Vo +
V
R0(1-x)
bridge
R0(1+x)
24
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone
Applicazione agli strain gages
R2
R1
- Vo +
V
R4
R3
25
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone
Applicazione agli strain gages: Dummy Gage
R0(1+y)
R0
- Vo +
V
R0
R0(1+x)(1+y)
R0 (1 + x )(1 + y )
V
V0 = V
− =
R0 (1 + x )(1 + y ) + R0 (1 + y ) 2
(
1 + x) V
2(1 + x ) − (2 + x )
=V
− =V
=
(1 + x ) + 1 2
2(2 + x )
x
=V
2(2 + x )
E’ scomparsa la dipendenza da y, e quindi
ad esempio dalla temperatura!!
26
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone
Strain gages: effetto della temperatura
Compensazione
dummy sensors
con
Entrambi i sensori variano
alla stessa maniera con la
temperatura ma danno un
contributo
opposto
alla
tensione di uscita
27
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: progettazione
Nel caso in cui il comportamento del ponte, per
un determinato sensore e nel range di misura
prescelto, non sia lineare è possibile ricorrere a
una linearizzazione analogica o digitale del
legame ingresso-uscita.
In realtà la linearizzazione non è essenziale per
la misurazione, purché il sistema fornisca risultati
riproducilibili.
Tuttavia
essa
semplifica
l’elaborazione dei segnali.
28
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone
Linearizzazione
•La linearità è una delle caratteristiche metrologiche
più interessanti di un sistema di misura.
•Oltre che linearizzare la caratteristica di trasduzione
è possibile considerare configurazioni circuitali
tramite cui ottenere una relazione intrinsecamente
lineare.
R0(1+x)
R0
R0
I
+
V
R0
I = (V − V / 2) / R0 =
+
Vo
R0(1+x)
R0
R0
V
R0
V
2R0
V
− R0 (1 + x )I
2
V V
V
Vo = − (1 + x ) = − x
2 2
2
Vo =
29
Circuiti di condizionamento per sensori resistivi
Il ponte di Wheatstone: linearizzazione
V/R0
V
I3
V*
R0(1+x)
R0
Vo
I1
V
R0 R0
I2
R
V
Ix
V0 = −RI x = −R (I1 + I 2 )
I1 =
V
V
, I3 =
R0
R0
V * = R0 (1 + x )I3 = V (1 + x )
V*
V (1 + x )
=−
I2 = −
R0
R0
da cui :
⎛ V V (1 + x ) ⎞ R
⎟=
−
Vx
V0 = -R(I1 + I2) = -R ⎜⎜
⎟
R0 ⎠ R0
⎝ R0
30