MOMENTO E COPPIA DI FORZE
Il momento di una forza rispetto ad un punto di rotazione è una grandezza vettoriale che ha
il modulo pari al prodotto del modulo della forza per il braccio della forza.
M=F•b
b
F
Il braccio di una forza rispetto ad un punto di rotazione è la minima distanza tra il punto e la
retta di azione della forza. La distanza si deve misurare sulla retta perpendicolare con la retta di azione della
forza passante per il punto di rotazione.
Il momento quindi è una grandezza che misura l’effetto rotazionale di una forza.
Il momento, nel Sistema Internazionale, si misura in newton per metro (Nm);
Una coppia di forze sono due forze parallele e discordi aventi lo stesso modulo.
Il momento di una coppia di forze è costante rispetto a qualunque punto di rotazione si consideri.
Esso è dato dal prodotto del modulo di una delle forze (F) per la distanza (d) delle loro rette di
azione.
d
M=F•d
F
F
L’ATTRITO
L’attrito è una resistenza (forza) passiva, in quanto compie sempre lavoro resistente. L’energia
consumata dall’attrito si trasforma in calore.
ATTRITO RADENTE:
L’attrito radente si ha quando un corpo striscia su un altro. Dipende dalla natura e dallo stato
delle due superfici a contatto, ma non dipende dall’area delle superfici a contatto.
Ar k r Fn
Dove (Ar) è l’attrito radente, (kr) è il coefficiente dell’attrito radente e (Fn) è la forza normale,
ovvero la forza che il corpo esercita perpendicolare sulla superficie con la quale si trova a
contatto;
ATTRITO radente STATICO: è la forza necessaria per far iniziare il moto;
ATTRITO radente CINETICO: è la forza necessaria per mantenere l’equilibrio dinamico;
ATTRITO VOLVENTE
L’attrito volvente si ha quando un corpo rotola su un altro.
1
Fn
R
Dove (Av) è l’ attrito volvente, (kv) è il coefficiente dell’attrito volvente, (Fn) è la forza normale,
(R) il raggio del corpo.
Av k v
ATTRITO NEL MEZZO
L’attrito nel mezzo si ha quando un corpo si muove all’interno di un fluido (un liquido o un
aeriforme). Esso dipende dalla velocità e dalla forma del corpo in movimento e dalla natura del
fluido.
Per basse velocità l’attrito è direttamente proporzionale alla velocità:
Am k1 V
Per alte velocità l’attrito dipende dal quadrato della velocità:
Am k 2 V 2
EQUILIBRIO DEI CORPI
MODELLI: CORPO RIGIDO, PUNTO MATERIALE
Nello studio dei fenomeni fisici la scienza si serve dei modelli.
Un modello è la semplificazione di un fenomeno reale. Le semplificazioni introdotte servono
a facilitare lo studio dei fenomeni naturali.
Per esempio, nello studio del movimento dei corpi si considera un modello in cui i corpi si muovono senza attriti.
Due modelli sono: il corpo rigido e il punto materiale
Un corpo si considera rigido se sotto l’azione di forze non si deforma e non si rompe.
Naturalmente il corpo rigido è un modello astratto, perché i corpi reali si deformano e si
rompono.
Un corpo reale si può considerare rigido se le deformazioni che subisce sono trascurabili rispetto
alle sue dimensioni.
Un altro modello è il punto materiale.
Il punto materiale è un corpo avente massa ma privo di volume.
Un corpo può essere considerato un punto materiale se le sue dimensioni sono trascurabili
rispetto alle distanze considerate nel fenomeno. (Esempio: l’automobile che percorre l’autostrada)
I VINCOLI
Un vincolo è qualunque causa che limita il movimento di un corpo.
Il vincolo per avere la sua funzione deve essere in grado di annullare l’effetto delle forze
applicate al corpo. La forza con cui reagisce il vincolo è detta reazione vincolare.
I vincoli ideali sono in grado di reagire a qualunque forza; i vincoli reali hanno un limite di
resistenza.
BARICENTRO
Il baricentro di un corpo è il punto di applicazione della forza peso del corpo. La forza peso
di un corpo è la risultante di tutte le forze peso delle piccole particelle di cui è costituito il corpo.
Il baricentro viene chiamato anche centro di gravità e si indica con la lettera G
EQUILIBRIO DEL CORPO RIGIDO
2
Un punto materiale è in equilibrio quando la risultante delle forze è nulla: F tot = 0
Un corpo rigido è in equilibrio se:
- la somma vettoriale di tutte le forze applicate al corpo è nulla : F tot = 0
- la somma vettoriale di tutti i momenti delle forze applicate al corpo è nulla: M tot = 0
CONDIZIONI DI EQUILIBRIO
L’equilibrio di un corpo può essere stabile, instabile e indifferente.
STABILE: se facendo fare un piccolo spostamento ad un corpo, esso ritorna nella
posizione iniziale.
INSTABILE: se facendo fare un piccolo spostamento ad un corpo, esso si allontana dalla
posizione iniziale.
INDIFFERENTE: se facendo fare un piccolo spostamento ad un corpo, esso resta nella
posizione variata.
MACCHINE SEMPLICI
Una macchina semplice è un dispositivo che permette di equilibrare due forze, una detta
forza motrice (Fm),o potenza, e l’altra detta forza resistente (Fr), o resistenza.
Il vantaggio si calcola dividendo la forza resistente con la forza motrice:
V
Fr
Fm
Una macchina è vantaggiosa se la forza motrice è minore della forza resistente:
Fm < Fr ossia Vantaggio V >1
Una macchina è svantaggiosa se la forza motrice è maggiore della forza resistente:
Fm > Fr ossia Vantaggio V <1
Una macchina è indifferente se la forza motrice è uguale alla forza resistente:
Fm = Fr ossia Vantaggio V = 1
3
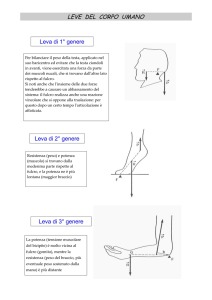
LE LEVE
Una leva è un corpo (asta rigida) girevole intorno ad un punto detto fulcro.
Una leva è in equilibrio se il momento della forza motrice è uguale al momento della forza
resistente, applicando questa uguaglianza si risolvono i problemi sulle leve:
Mm =Mr
Fm • bm = Fr • br
La leva è di primo genere se il fulcro è posto tra la forza motrice e la forza resistente.
Fm
Fr
La leva di primo genere può essere:
Vantaggiosa: se il fulcro è posto più vicino alla forza resistente;
Svantaggiosa: se il fulcro è posto più vicino alla forza motrice;
Indifferente: se il fulcro è posto nel mezzo tra la forza motrice e la forza resistente.
La leva è di secondo genere se il fulcro è posto ad un estremo e la forza resistente è posta tra il
fulcro e la forza motrice.
Fr
Fm
La leva di secondo genere è sempre vantaggiosa; al limite è indifferente se la forza motrice e
resistente sono applicate nello stesso punto.
La leva è di terzo genere se il fulcro è posto ad un estremo e la forza motrice è posta tra il fulcro
e la forza resistente.
Fm
Fr
La leva di terzo genere è sempre svantaggiosa; al limite è indifferente se la forza motrice e la
forza resistente sono applicate nello stesso punto.
4
CARRUCOLA FISSA
La carrucola fissa è una ruota che gira attorno ad un asse, disposto normalmente e al centro
della ruota, sostenuta da una staffa fissata ad un vincolo.
Fr
Fm
La carrucola serve a variare la direzione di una forza, mentre il modulo della forza non viene
modificato.
La carrucola fissa, è una macchina indifferente poiché la forza motrice è uguale alla forza
resistente:
Fm = Fr
La carrucola fissa equivale ad una leva di primo genere indifferente (i due bracci sono uguali).
CARRUCOLA MOBILE
La carrucola mobile è una carrucola che scorre lungo una corda con un capo fissato ad un
vincolo.
Fm
Fr
La forza resistente (Fr) è applicata nella staffa attaccata all’asse della carrucola, mentre la forza
motrice è applicata al capo libero della fune.
E’ una macchina vantaggiosa poiché la forza motrice è uguale alla metà della forza resistente:
F
Fm r
2
Fr
Quindi il vantaggio ( V
) per la carrucola mobile è uguale a 2.
Fm
La carrucola mobile equivale ad una leva di secondo genere che ha la forza resistente posta nel
punto di mezzo tra il fulcro e la forza motrice.
5
STATI DELLA MATERIA
In natura i corpi si posso presentare in tre stati:
-
solido: i solidi hanno forma e volume propri;
liquido: i liquidi hanno volume proprio e la forma del recipiente che li contiene;
aeriforme: gli aeriformi non hanno né forma e né volumi propri e sono comprimibili.
I liquidi e gli aeriformi sono detti anche fluidi perché hanno la proprietà di poter “fluire”
attraverso un foro o un tubo.
DENSITÀ E PESO SPECIFICO
La densità è il rapporto tra la massa di un corpo ed il volume che la massa occupa.
Densità = massa : volume
m
V
Le formule inverse sono:
m = ρx V
e
V
m
L’unità di misura della densità nel S.I. è kg/m3
Il peso specifico è il rapporto tra il peso di un corpo ed il suo volume
Peso specifico = peso : volume
Fp
V
L’unità di misura del peso specifico nel S.I. è N/m3 ma si misura anche in kgf/m3
Il peso specifico si calcola anche con la densità:
Peso specifico = densità x accelerazione di gravità
γ = ρx g
dove g = 9,81 m/s² è l’accelerazione di gravità.
6
IDROSTATICA
L’idrostatica è il capitolo della fisica che studia l’equilibrio dei corpi fluidi (liquidi ed aeriformi)
LA PRESSIONE
La pressione è data dal rapporto tra il modulo della forza agente perpendicolarmente su
una superficie e l’area della superficie stessa.
p
Pressione = forza perpendicolare : area della superficie
F
S
Dove (p) è la pressione, (F) è la forza ed (S) è l’area.
La pressione, nel Sistema Internazionale, si misura in pascal (Pa): 1Pa
Altra unità di misura, non del S.I., è l’atmosfera (atm): 1atm
1kg p
1cm
2
1N
1m 2
10 5 Pa
LEGGE DI PASCAL
La pressione esercitata su una qualunque superficie di massa fluida si trasmette in tutti i
punti, in tutte le direzioni e con lo stesso valore.
Un’applicazione del principio di Pascal il torchio idraulico
LEGGE DI STEVINO
La pressione idrostatica è direttamente proporzionale all’altezza (h) della colonna di fluido
sovrastante e alla densità (ρ) del fluido stesso.
p g h
7
La pressione idrostatica è la pressione dovuta al peso proprio del fluido.
Per la legge di Stevino la pressione ad una data profondità dipende solo dalla densità e dalla
profondità dal livello del liquido e non dipende dalla forma del recipiente.
Una conseguenza della legge di Stevin è il principio dei vasi comunicanti:
Il livello del liquido in più vasi comunicanti è sempre lo stesso anche se varia la forma del
recipiente.
PRINCIPIO DI ARCHIMEDE
Un corpo immerso in un liquido è soggetto a una forza diretta
dal basso verso l’alto (verticalmente), il cui modulo è uguale al
peso del liquido spostato.
Fa = ρl x g x Vci
Dove Fa è la spinta di Archimede, (ρl) è la densità del liquido, g è l’accelerazione di gravità
(=9,81m/s²) e (Vci) è il volume del corpo immerso.
A) Un corpo affonda se il suo peso (forza peso Fp) è
maggiore della spinta di Archimede Fa;
ossia la densità del corpo ρc è maggiore della densità
del liquido ρl
Fp > Fa
ρ c > ρl
B) Un corpo resta in sospensione se il suo peso (forza
peso Fp) è uguale alla spinta di Archimede Fa;
ossia la densità del corpo ρc è uguale alla densità del
liquido ρl
Fp = Fa
ρ c = ρl
C) Un corpo galleggia se il suo peso (forza peso Fp) è
minore della spinta di Archimede Fa;
ossia la densità del corpo ρc è minore della densità del liquido ρl
La forza peso Fp di un corpo si calcola:
Fp = ρc x g x Vc
8