Il problema ad N-corpi
Primo Levi -Roberto Bedogni
INAF Osservatorio Astronomico di Bologna
via Ranzani, 1 40127 - Bologna - Italia
Tel, 051-2095721 Fax, 051-2095700
http://www.bo.astro.it/~bedogni/primolevi
Email :[email protected]
Il problema ad N-Corpi
La stabilità planetaria a lungo
termine
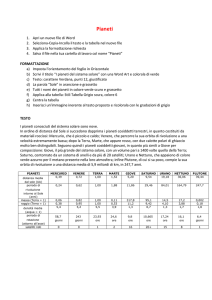
Costanti astronomiche fondamentali IAU
Stabilità dei sistemi planetari
Problema :
Una massa puntiforme è circondata da N corpi di massa più piccola in orbite
quasi circolari e complanari. Questa configurazione è stabile per lungo periodi
orbitali (ad es 1010 orbite)?
Le domande che stanno alla base di questo problema sono:
Come si formano i pianeti?
Perché nel sistema solare ci sono “pochi” pianeti?
Perché esistono zone ripulite dalla presenza di pianeti ?
Quale è il destino della Terra?
Da dove vengono meteoriti, comete e Centauri ?
Perché la formazione planetaria è così rapida nel primo 0,1% della sua vita?
I pianeti extrasolari come si interfacciano con questi comportamenti?
I sistemi planetari sono invariati dalla loro formazione o la loro dinamica si
evolve?
Come si comportano i sistemi dinamici su lunghi periodi di tempo ?
Il problema ad N-Corpi: le equazioni del moto
a GR correzione dovuta alla Relatività Generale per un potenziale
gravitazionale ~ GM/c 2r < 10 -8
as correzioni dovute alla presenza dei satelliti
mi masse dei pianeti determinate con una precisione migliore di 10-9 M
Le condizioni iniziale sono state determinate con grande accuratezza sia sulle
distanze che sui valori di velocità angolare
Le equazioni del moto
Incertezze
• asteroidi (< 10-9)
• momento di quadrupolo solare (< 10-10, anche per Mercurio)
• perdita di massa del Sole (<10-14)
• forze mareali galattiche ( <10-13)
• stelle vicine (a ~ 500 U.A. il passaggio più vicino)
L’approssimazione appare molto buona e le condizioni iniziali per il
problema agli N-corpi sono ben note
Basterebbe quindi integrare per ~1010 orbite (cioè 4,5109 anni indietro
verso la formazione sino a 7109 anni in avanti sino alla fase evolutiva del
Sole di gigante rossa) per ricostruire il passato ed il futuro del Sistema
solare
Le equazioni del moto
E’ a questo punto che sorgono le difficoltà legate ai metodi numerici
di integrazione ma anche al fatto che il problema agli N-Corpi è
intrinsecamente fonte di non-linearità, caoticità e quindi
comportamenti stocastici fortemente imprevedibili
Calcolo delle
orbite planetarie
con tre differenti
integratori
numerici
Calcolo delle
orbite
planetarie con
quattro
differenti
integratori
numerici
Pianeti interni eccentricità Ito & Tanikawa
(2002)
Pianeti interni inclinazione orbitale Ito & Tanikawa
(2002)
Orbita peculiare di Plutone
Plutone ha:
•La maggiore eccentricità (e = 0,250 )
•La maggiore inclinazione( i = 17o )
•Una distanza al perielio q = a(1 – e) = 29,6 UA minore del semiasse
maggiore di Nettuno ( a = 30,1 AU )
Perché non collidono ?
Risonanza orbitale tra le orbite di Plutone e Nettuno
Periodo orbitale di Plutone = 247,7
anni
Periodo orbitale di Nettuno = 164,8
anni
247,7/164,8 = 1,50 = 3/2
La risonanza 3:2 assicura che
quando Plutone è al perielio risulta a
circa 90° lontano da Nettuno
TNOs (Trans-Neptunian-Object)-Plutini e migrazioni
eccentricità
inclinazione
•All’inizio nel Sistema solare
abbondavano i planetesimi il cui
accrescimento ha prodotto i pianeti
•Nettuno ha spostato i planetesimi residui
verso orbite più esterne
•Se Plutone era inizialmente a bassa
eccentricità e bassa inclinazione in
un’orbita esterna ha inevitabilmente
risentito della risonanza 3:2 con Nettuno
•Una volta catturato l’inclinazione e
l’eccentricità di Plutone hanno
incominciato a crescere portando sempre
più verso l’esterno
•Altri corpi minori possono essere
catturati dalla risonanza di Nettuno
risonanza
Malhotra (1993)
TNOs
descrizione
Oggetti della fascia di
Kuiper
Plutini (3:2)
Centauri
Comete
ottobre 2003 (Minor
Planet Center)
Elementi orbitali
Il calcolo delle orbite
Gli elementi orbitali
I 6 elementi orbitali, necessari a
definire un'orbita, sono:
1. il semiasse maggiore a
2. l'eccentricità e
3. l'inclinazione i
4. la longitudine del nodo
ascendente O
5. la distanza angolare tra perielio
e nodo è o
6. l'istante T del passaggio al
perielio
Per individuare un'orbita sono
necessarie almeno 3
osservazioni che fissino 3
coppie di valori (3 coordinate
nel sistema eclitticale). Con
questi dati è possibile trovare i
sei elementi orbitali, incogniti.
La formazione della Luna una migrazione verso
l’interno del Sistema solare
Successione temporale di un impatto
non frontale, quando l'oggetto che urta
la Terra ha una massa del 13% di quella
terrestre. I tempi sono in ore per le
immagini da a) a k) e valgono 0,110,32-0,86-1,40-2,16-4,85-5,93-13.4818,87- 21,02 e 26,95, rispettivamente.
La scala di colore definisce la
temperatura delle particelle (detriti) e
sono in gradi Kelvin (°K). Le immagini da
a) a k) guardano il sistema dall'alto. Le
particelle rosse hanno una temperatura
maggiore di 6440°K e le distanze sono in
unità di 1000 Km. L'immagine l) presenta
la visione di lato dopo 27 ore e le
temperature sono modificate in modo
che il colore rosso mostri una
temperatura di 9110°K.
Migrazioni nel Sistema solare
Migrazioni nel Sistema solare
Migrazioni nel Sistema solare