ANGOLI AL CENTRO E ANGOLI ALLA CIRCONFERENZA
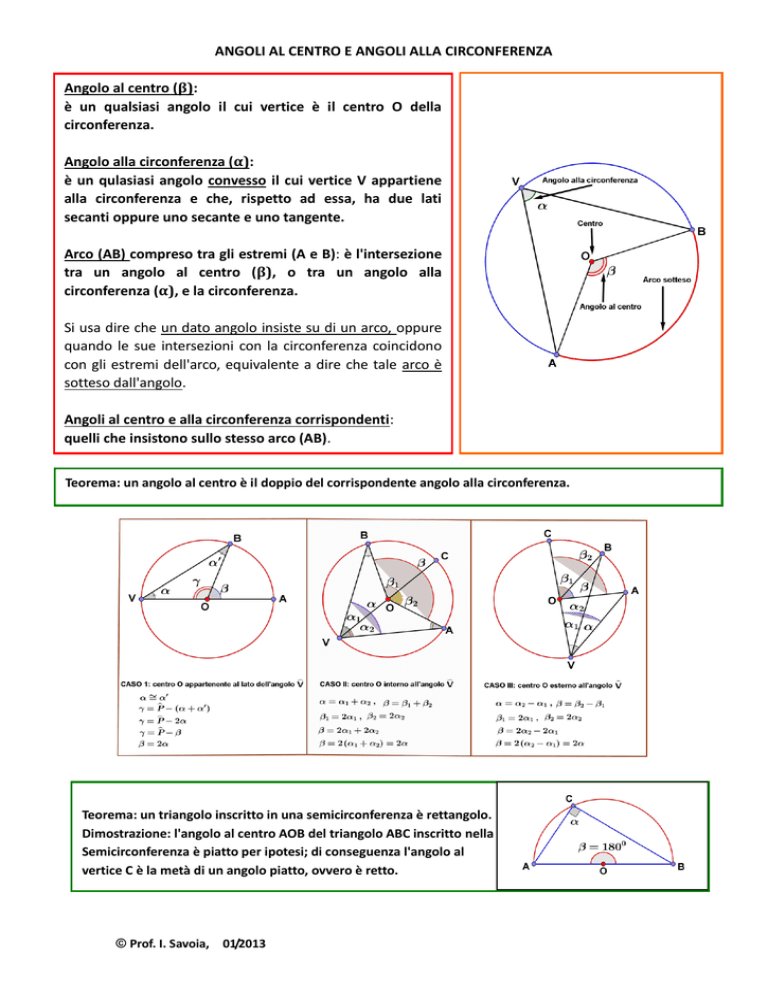
Angolo al centro (β):
è un qualsiasi angolo il cui vertice è il centro O della
circonferenza.
Angolo alla circonferenza (α):
è un qulasiasi angolo convesso il cui vertice V appartiene
alla circonferenza e che, rispetto ad essa, ha due lati
secanti oppure uno secante e uno tangente.
Arco (AB) compreso tra gli estremi (A e B): è l'intersezione
tra un angolo al centro (β), o tra un angolo alla
circonferenza (α), e la circonferenza.
Si usa dire che un dato angolo insiste su di un arco, oppure
quando le sue intersezioni con la circonferenza coincidono
con gli estremi dell'arco, equivalente a dire che tale arco è
sotteso dall'angolo.
Angoli al centro e alla circonferenza corrispondenti:
quelli che insistono sullo stesso arco (AB).
Teorema: un angolo al centro è il doppio del corrispondente angolo alla circonferenza.
T
Teorema: un triangolo inscritto in una semicirconferenza è rettangolo.
Dimostrazione: l'angolo al centro AOB del triangolo ABC inscritto nella
Semicirconferenza è piatto per ipotesi; di conseguenza l'angolo al
vertice C è la metà di un angolo piatto, ovvero è retto.
© Prof. I. Savoia, 01/2013












