Calcolo combinatorio. Attività1
Sulle disposizioni
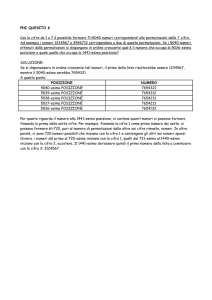
1. Per aprire una cassaforte bisogna comporre, con le 10 cifre decimali, un numero di 8
cifre, con ripetizione. Rispondi ai seguenti quesiti:
a. Quanti sono i numeri da provare? ...................
b. Per provare un numero impieghi 8 secondi; quanto tempo dovresti impiegare per
provarle tutti i numeri? Dai la risposta in secondi e in anni.
Tempo in secondi = ……
Tempo in anni:…………………………………………………………………….
2. Con le 5 cifre dispari formi tutti i numeri di 3 cifre con ripetizione e cancelli tutti i
numeri senza cifre ripetute; quanti numeri ti rimangono? Completa il procedimento.
- I numeri di tre cifre con ripetizione sono ………. = …..
- I numeri di tre cifre senza ripetizione sono ………… = ……
- Rimangono ………….. - ……………. = …….. numeri.
3. È data la seguente equazione.
Dx,5 = 3Dx,4
Risolvi i quesiti qui sotto.
a. Quali numeri possono essere soluzioni dell’equazione?
………………………………………………………………………………………..
b. Completa qui sotto il procedimento per risolvere l’equazione
x ⋅ (x – 1) ⋅ ………………………. = 3x ⋅ (x – 1) ⋅ ……………………………
…………………………………………………………………………………………
Sulle permutazioni
4. Quante sono le permutazioni delle 5 lettere della parola PINZA? Completa la risposta
qui sotto.
P5 = …. = …..
5. Nella parola PINNA, fra le 5 cinque lettere, ne trovi 2 uguali (N); quante sono ora le
permutazioni? Completa il seguente ragionamento.
Immagino di aver elencato tutti i P5,2 raggruppamenti che si ottengono in questo caso.
In ogni raggruppamento, in quanti modi posso permutare le due lettere N? …..
Se ripeto il procedimento su tutti i raggruppamenti ottengo le P5 permutazioni iniziali.
Trovo dunque:
........
….. ⋅ P5,2 = P5 da cui P5,2 =
........
Il ragionamento seguito ha carattere generale e porta a concludere che il numero Pn,k
permutazioni di n oggetti, di cui k uguali fra loro, è dato da:
€
6. Nella parola NONNO, fra le 5 lettere ne trovi 3 uguali fra loro (N) e le altre 2 sono
pure uguali fra loro (O); quante sono ora le permutazioni?
......
P5,3,2 =
......
Daniela Valenti, Treccani Scuola
€
1 Sul fattoriale
n! = 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ (n – 1) ⋅ n
7. Completa con carta e penna i seguenti calcoli
1! = ….
2! = …… = ……
3! = ………… = ….
Osserva che:
2! = …. ⋅ 1!
3! = ….⋅ 2!
Dimostra che risulta vera la seguente uguaglianza per ogni numero naturale n ≥ 1:
(n + 1)! = (n + 1) ⋅ n! (*)
………………………………………………………………………………………….
8. Che cosa ottieni, se sostituisci 0 a n nella uguaglianza (*)?
Completa il procedimento qui sotto per rispondere
I membro: ( …. + 1)! = ….. = ….
II membro: ( …. + 1) ⋅ ….! = ……⋅ ….! = …..
I matematici hanno stabilito di estendere la relazione (*) al caso n = 0; spiega come
conviene scegliere il risultato di 0!
…………………………………………………………………………………………….
9. Applica opportunamente l’uguaglianza (*) per completare con carta e penna il calcolo
delle seguenti espressioni
(2 ⋅ 3)!
= ......
2!⋅3!
10. Con l’aiuto del tascabile completa la seguente tabella per capire quanto rapidamente
cresce il fattoriale di un numero.
0
1
2
3
4
5
6
7€
8
9
10
n
n!
11. Anche il numero della disposizioni semplici può essere espresso con il fattoriale.
Completa la spiegazione seguente.
7!
Esempio: D7,4 =
I membro D7,4 = 7 ⋅ ……………..
3!
7! 7 ⋅ 6 ⋅ .....
II membro =
= ........
3!
3!
n!
In €
generale: Dn,k =
I membro Dn,k = n ⋅ (n – 1) ⋅ ……………..
(n − k)!
II membro
€
n ⋅ (n −1) ⋅ ....⋅ (n − k + 1) ⋅ (n − k ) ⋅ ....⋅1
n!
=
=
n
−
k
!
n
−
k
!
(
)
(
)
€
= ........................................................................
Daniela Valenti, Treccani Scuola
€
2