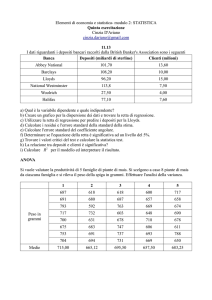
PROBLEMI: DISTRIBUZIONE BINOMIALE
1. La probabilità che un cliente che entra in un negozio di elettrodomestici compri un computer è
del 20%. Considerando che nel negozio ci sono 7 clienti:
a) costruire la distribuzione di probabilità e la funzione di ripartizione;
b) calcolare il valore atteso;
c) calcolare lo scarto quadratico medio.
2. Supponiamo di trasferire tre (dieci, trenta, cinquanta) pacchetti di dati su una linea difettosa. La
probabilità che un pacchetto trasferito lungo tale linea risulti corrotto è 0,1, e quindi la probabilità
di trasferire un pacchetto con successo è 0,9.
a. Qual è la probabilità che nessun pacchetto risulti corrotto?
b. Qual è la probabilità che almeno due pacchetti siano corrotti?
c. Qual è la probabilità che non tutti e tre i pacchetti risultino corrotti?
3. In un'officina sono installate 5 macchine uguali, ciascuna ha probabilità del 20% di guastarsi.
Studiare la variabile casuale X = numero di macchine guaste simultaneamente.
a. Qual è la probabilità che solo una macchina si guasti?
b. Qual è la probabilità che tutte le macchine si guastino contemporaneamente?
4. La probabilità che un paziente non si riprenda da un particolare intervento è di 0,1.
a) Qual è la probabilità che esattamente 2 dei prossimi 8 pazienti che subiranno questo intervento
non si riprendano?
b) Qual è la probabilità che al massimo 1 degli 8 pazienti non si riprenda?
c) Qual è la probabilità che almeno 2 degli 8 pazienti non si riprenda?
d) La probabilità che esattamente 1 dei prossimi 4 pazienti non si riprenda è la medesima del
punto a)?
5.Un tecnico dell’IMQ, Istituto Marchio di Qualità, estrae da un lotto 5 lampadine con riposizione.
Si sa che, secondo il fabbricante, la probabilità che una lampadina pesi più di 20 grammi è 0.4.
a) Calcolare il valore atteso e la varianza del peso delle 5 lampadine.
b) Calcolare la probabilità che non più di 2 fra esse abbiano un peso superiore a 20 grammi.
c) Calcolare la probabilità che meno di 3 fra esse abbiano un peso superiore a 20 grammi.
d) Calcolare la probabilità che almeno 3 fra esse abbiano un peso superiore a 20 grammi.
e) Calcolare la probabilità che più di 2 fra esse abbiano un peso superiore a 20 grammi.
6. Cinque cavie appartenenti ad una stessa figliata sono sofferenti di una deficienza di vitamina A.
Essi vengono nutriti di una certa dose di carote. Sia p=0.73 la probabilità di guarigione. Ci
domandiamo:
a) Qual è la probabilità che tre delle cinque cavie guariscano?
b) Qual è la probabilità che almeno una cavia guarisca?
c) Qual è la probabilità che al più una cavia guarisca?