PERCORSO ANGOLO 2° PARTE
Questo percorso riprende l’ultima parte scritta da Rossana nel percorso “Dalle proprietà di liquidi e
solidi ai concetti di parallelismo e angolo” modificandola e proseguendola.
TEMATICHE AFFRONTATE: confronto di angoli, l’ampiezza dell’angolo, angolo come rotazione,
classificazione, misurazione,
TEMATICHE DA APPROFONDIRE gli angoli nei triangoli e nei quadrilatero, divisori e multipli
1 Siamo in classe quarta. I bambini sono capaci di riconoscere e disegnare linee orizzontali,
verticali, oblique, parallele e incidenti; sanno che linee incidenti formano angoli ma ancora non è
chiaro cosa veramente in matematica intendiamo con la parola angolo.
Proponiamo un’esperienza dove, attraverso il confronto di due angoli, la riflessione si concentra
sulle loro proprietà percettive al fine di individuare quella determinante (ampiezza) e scartare
quella insignificante (lunghezza).
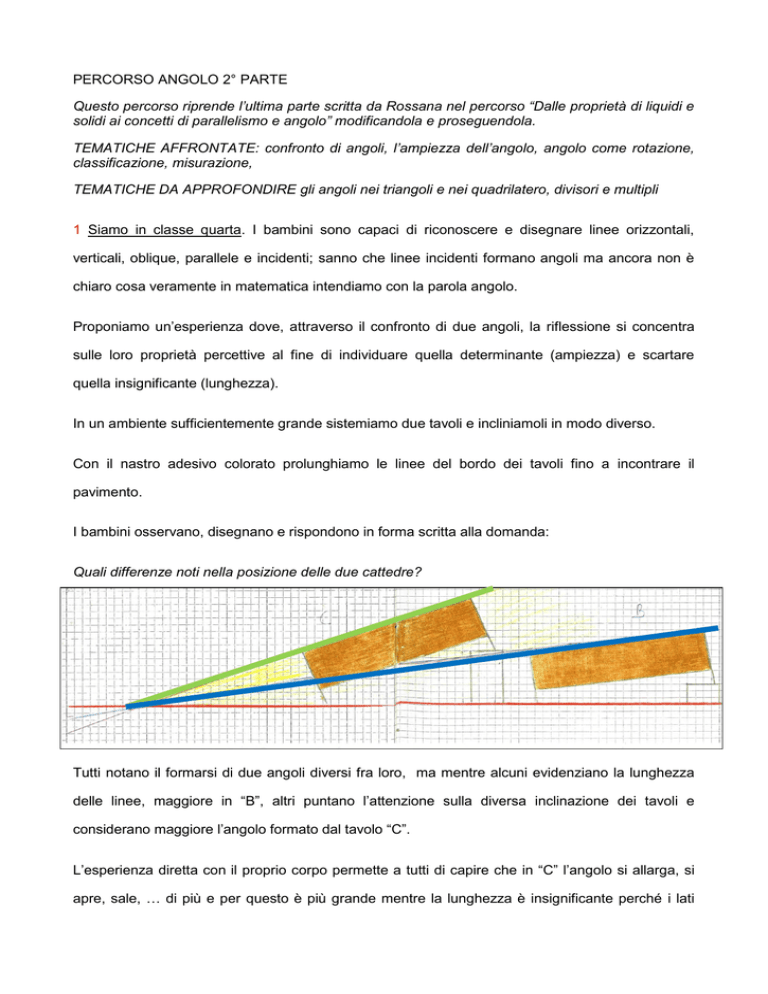
In un ambiente sufficientemente grande sistemiamo due tavoli e incliniamoli in modo diverso.
Con il nastro adesivo colorato prolunghiamo le linee del bordo dei tavoli fino a incontrare il
pavimento.
I bambini osservano, disegnano e rispondono in forma scritta alla domanda:
Quali differenze noti nella posizione delle due cattedre?
Tutti notano il formarsi di due angoli diversi fra loro, ma mentre alcuni evidenziano la lunghezza
delle linee, maggiore in “B”, altri puntano l’attenzione sulla diversa inclinazione dei tavoli e
considerano maggiore l’angolo formato dal tavolo “C”.
L’esperienza diretta con il proprio corpo permette a tutti di capire che in “C” l’angolo si allarga, si
apre, sale, … di più e per questo è più grande mentre la lunghezza è insignificante perché i lati
sono semirette (cioè di lunghezza infinita). Puntualizziamo che quando un angolo si allarga, si
apre, sale, … di più in matematica si dice che è più ampio.
2 Costruiamo i modellini in cartone dei due angoli e distribuiamoli con la seguente consegna
individuale:
Tutti siamo d’accordo nel dire che
•
L’angolo B è più lungo
•
L’angolo C è meno lungo
•
L’angolo B è meno ampio
•
L’angolo C è più ampio
Qual è l’angolo più grande?
I bambini sovrappongono e confrontano per verificare che la grandezza di un angolo non dipende
mai dalla lunghezza dei suoi lati che posso prolungare quanto voglio, ma dall’inclinazione degli
stessi; la proprietà che determina la grandezza dell’angolo è quindi l’ampiezza.
Usando le parole scritte dai bambini e la conclusione a cui siamo arrivati attraverso la discussione
elaboriamo una scheda di sintesi da studiare.
3 Consegniamo ad ogni alunno due barrette di diverso colore unite ad una estremità e
sollecitiamoli a costruire angoli di diversa ampiezza. Dopo pochi minuti di attività libera diamo le
seguenti indicazioni di lavoro:
•
Fai coincidere le bacchette
•
Tieni ferma una bacchetta e cambia l’inclinazione dell’altra
•
Fai in modo di costruire angoli sempre più ampi
•
Disegna sul quaderno alcuni angoli costruiti con le bacchette ordinandoli dal meno ampio al
più ampio
•
Evidenzia l’angolo del rettangolo
4 Predisponiamo attività per controllare se nel confrontare gli angoli gli alunni considerino
l’ampiezza o siano sempre condizionati dalla lunghezza dei lati.
Eccone alcuni esempi:
Ritaglia, confronta e ordina dal minore al maggiore.
Incolla l’ordinamento sul quaderno e prolunga per quanto ti è possibile i lati degli angoli
Ritaglia, confronta e ordina dal minore al maggiore.
Incolla l’ordinamento sul quaderno e prolunga per quanto ti è possibile i lati degli angoli.
Hai scoperto qualcosa? Scrivi (esistono 3 gruppo di angoli di uguale ampiezza)
5 Di nuovo lavoriamo con le aste e concentriamoci sugli angoli che maggiormente hanno
incuriosito i bambini. Individualmente costruiscono e disegnano in posizioni diverse angoli nulli,
retti, piatti e giro. L’attenzione al disegno e all’organizzazione degli spazi nel foglio è importante.
Per stimolare la concentrazione possiamo domandare:
Quali azioni sono necessarie per formare un angolo con le aste?
Dalla discussione deve emergere che quando cambio l’inclinazione di un’asta rispetto all’altra
faccio una rotazione. La rotazione viene disegnata attraverso una freccia.
Attraverso domande stimolo cerchiamo di individuare relazioni fra questi angoli. Esempio: l’angolo
retto è ¼ dell’angolo giro, l’angolo piatto è il doppio dell’angolo retto, …
A questo punto del lavoro raccogliamo le conoscenze più significative in una scheda di sintesi da
inserire nei quaderni individuali. Un possibile esempio di scheda di sintesi può essere il seguente:
Sappiamo che…..
Due SEMIRETTE (o LATI) unite in un punto formano UN ANGOLO
I NOMI CORRETTI DEGLI ELEMENTI DI UN ANGOLO
Lato o semiretta (linea)
Ampiezza dell’angolo (piano)
Vertice (punto)
Lato o semiretta (linea)
QUANDO IN UN ANGOLO CAMBIA LA POSIZIONE DI UN LATO RISPETTO
ALL’ALTRO SI DICE CHE CAMBIA L’INCLINAZIONE FRA I 2 LATI.
LA MAGGIORE O MINORE AMPIEZZA DI UN ANGOLO DIPENDE
DALL’INCLINAZIONE DEI SUOI LATI;
NON DIPENDE DALLA LORO LUNGHEZZA.
MAGGIORE E’ L’INCLINAZIONE, MAGGIORE E’ L’ AMPIEZZA
DELL’ANGOLO
QUESTO CAMBIAMENTO DI INCLINAZIONE PUÒ AVVENIRE ATTRAVERSO
UNA ROTAZIONE
SI VEDE BENISSIMO GUARDANDO LE LANCETTE DELL’OROLOGIO
6 Distribuiamo a tutti i bambini due bacchette, un modello di angolo retto
disegnare raggruppamenti di angoli seguendo le seguenti indicazioni:
1. Angoli minori dell’angolo retto
2. Angoli retti
3. Angoli maggiori dell’angolo retto e minori dell’angolo piatto
4. Angoli piatti
5. Angoli maggiori dell’angolo piatto e minori dell’angolo giro
Informiamo i bambini che tutti
gli angoli minori del retto si
chiamano acuti mentre quelli
maggiori del retto e minori del
piatto si chiamano ottusi.
Aspettiamo a dare un nome
agli angoli maggiori del piatto e
minori del giro; angoli questi
percettivamente meno evidenti
soprattutto se non costruiti
attraverso la rotazione della
bacchetta
e un righello per
7 Per rinforzare le conoscenze proponiamo alcune prove Invalsi da svolgere individualmente. Le
prime due sono relative al nome degli angoli mentre le altre richiedono la capacità di fare delle
rotazioni; Non avendo ancora affrontato la misura è necessario dire ai bambini che 90° è la
rotazione con cui si forma l’angolo retto mentre con 180° si forma il piatto.
Segna il punto dove guarda Piero
8 Per dare un nome anche agli angoli maggiori del piatto e minori del giro usiamo un breve testo
tratto da un libro di matematica:
Un angolo si chiama CONVESSO quando, comunque si prendano due punti appartenenti ad esso,
la linea retta che li unisce è contenuta nell’angolo.
Invitiamo i bambini a disegnare le varie tipologie di angolo e a provare
ad applicare questo criterio. È subito evidente che solo il gruppo degli
angoli compresi fra il piatto e il giro non sono convessi perché ci sono
rette (che uniscono coppie di punti) che passano fuori dall’angolo.
Informiamo che questi angoli si chiamano concavi.
Adesso tutti sanno che gli angoli si dividono in concavi (< di 360° ; >
180°) e convessi (nulli, acuti, retti, ottusi, piatti e giro)
NON
CONVESSI
CONCAVI
9 Osservando gli angoli concavi i bambini scoprano l’esistenza di due angoli aventi la stessa
origine e gli stessi lati. Concludiamo questa prima parte con attività volte a considerare “l’altro
angolo” e al termine diamo una scheda di sintesi da studiare.
RICORDA
Se osservo due semirette
unite in un vertice vedo
sempre due angoli.
In questi casi uno è convesso
(retto, acuto, ottuso) e
l’altro non è convesso
Vediamo adesso i casi speciali
Ci sono 2 angoli:
Angolo nullo
nullo e giro
Ci sono 2 angoli piatti
Angolo piatto
Angolo giro
Anche qui ci sono 2
angoli: giro e nullo
CONCLUDIAMO
Due semirette unite in un vertice formano sempre due angoli.
Questi due angoli insieme formano sempre un angolo giro
10 Proponiamo un’esperienza che, collegando le conoscenze già acquisite all’osservazione diretta
della rotazione di un’ombra, conduca i bambini alla scoperta dell’unità di misura e alla successiva
misurazione degli angoli.
In un giorno di cielo sereno sistemiamo in giardino,
appoggiato su un grande foglio bianco, uno
strumento fatto da un piano orizzontale e un’asta
verticale. Ad intervalli regolari di un’ora segniamo
l’ombra dell’asta sul foglio e per riflettere su ciò che
accade poniamo domande stimolo a cui i bambini
rispondano in forma scritta e attraverso il disegno.
Per giungere a risultati significativi questa
esperienza deve avere la durata minima di 6 ore
quindi è probabile che occorra la collaborazione di
una collega di classe.
Iniziamo l’esperienza
Alle 8,30 scendiamo in giardino dove i bambini
notano l’ombra dell’asta proiettata sul foglio e la
ripassano.
Dopo un’ora torniamo in giardino e segniamo la
nuova posizione dell’ombra.
Sul quaderno eseguono la consegna:
Disegna quello che hai visto e spiega quello che hai
potuto capire.
Osserviamo alcuni disegni e confrontiamo le risposte.
Tutti notano che l’ombra ha cambiato posizione e collegano questo fenomeno alla posizione del
sole nel cielo. Diamo importanza a coloro che evidenziano la formazione dell’angolo e in
particolare a quelli che parlano di rotazione. In questa fase o nelle successive i bambini notano che
l’ombra ruota come le lancette
insieme scriviamo (esempio di testo collettivo)
dell’orologio e collegano l’ombra e i
• l’ombra ruota come le lancette dell’orologio quindi
suoi angoli alla misurazione del tempo.
si sposta in senso orario, forse l’uomo vedendo
come cambia posizione l’ombra ha costruito i
Alle 11,30 dopo quattro osservazioni i
primi strumenti per misurare il tempo
bambini individualmente disegnano e
• ogni ora l’ombra aumenta l’ampiezza dell’angolo
scrivono cosa hanno capito; dal
della stessa misura (questa è un’ipotesi da
confronto delle risposte produciamo un
verificare)
primo testo collettivo.
Per evitare errori chiediamo sempre che angolo ha formato la rotazione dell’ombra; infatti i bambini
tendono, già dopo tre ore, a disegnare un angolo retto mentre se osservano bene è evidente che
l’angolo è ancora acuto.
Alle 14,30 alla settima registrazioni (sono trascorse 6 ore dall’inizio dell’esperienza) la rotazione
dell’ombra ha disegnato un angolo retto.
11 Riutilizzando i materiali prodotti durante la giornata realizziamo una scheda riepilogativa utile
per ulteriori riflessioni matematiche
È a tutti evidente che l’uomo per organizzare il tempo studia la rotazione delle ombre e
contemporaneamente impara a misurare gli angoli.
L’angolo ora, 1/24 dell’angolo giro, è una prima unità di misura ma è
troppo grande.
Per misurare con precisione occorre costruire un’unità più piccola
che ci permetta di misurare con esattezza l’ampiezza degli angoli.
12 Proponiamo ai bambini la lettura di un testo.
UN PO’ DI STORIA
Un problema che interessava molto i popoli della Mesopotamia (Sumeri e Babilonesi) era la
misura del tempo.
Avevano osservato che i fenomeni legati al tempo mostravano un “ciclo”, cioè si verificavano e si
ripetevano a intervalli costanti.
L’idea era che questi fenomeni ciclici fossero rappresentati da un cerchio.
Successivamente il cerchio, che rappresentava il fenomeno più lungo, fu diviso
in parti uguali che indicavano periodi più brevi.
Oggi diremmo che il giorno rappresentato dal cerchio viene diviso in 24 parti e
ogni parte è un’ora.
Ma non fu subito così ...
I Sumeri e poi i Babilonesi divisero il cerchio/giorno in 12 parti uguali e successivamente
suddivisero ciascuna di queste parti in 30 parti più piccole.
In precedenza, avevano già diviso l'anno in 12 mesi e i mesi in 30 giorni.
Distribuiamo a ciascun bambino il cerchio diviso in 24 angoli/ora e poniamo la
seguente richiesta:
Parti dall’angolo giro diviso in 24 angoli per costruire lo strumento di misurazione
del tempo usato in Mesopotamia.
Scrivi come hai lavorato.
Tutti i bambini iniziano con l’accoppiare gli angoli/ora e così facendo dividono il cerchio in 12 parti
ottenendo la suddivisione del cerchio uguale al nostro orologio. Successivamente cercano di
suddividere questo dodicesimo di angolo giro in 30 parti. Il compito è difficile. Proponiamo di
lavorare in gruppi di 3 o 4 bambini in modo che sia subito possibile il confronto di strategie.
Prolungando i lati viene costruito un modello più grande dell’angolo da dividere; molti si avvicinano
alla soluzione ma se lavorano « a occhio» può capitare che gli angoli formati non siano 30 e
neppure uguali fra loro.
La soluzione arriva
dall’uso delle misure
lineari, e in particolare da
chi vede l’angolo come un
settore di cerchio chiuso
da un arco di 30 cm.
Se tutti i gruppi si limitano
a dividere ad occhio
problematizziamo le loro
soluzioni e forniamo il
modello del settore con
arco di 30cm in modo da
costruire agevolmente i 30
angoli grado
13 Poniamo individualmente le seguenti domande scritte, confrontiamo le risposte di ciascuna
domanda prima di passare alla successiva.
Quanti gradi in un angolo ora? Scrivi il perché della risposta
Quanti gradi in un angolo retto? Scrivi il perché della risposta
Quanti gradi in un angolo piatto? Scrivi il perché della risposta
Quanti gradi in un angolo giro? Scrivi il perché della risposta
Quanti gradi in un angolo nullo? Scrivi il perché della risposta
Conosci lo strumento che viene usato per misurare l’ampiezza degli angoli?
Distribuiamo a ciascun
bambino un
goniometro e dopo
averlo osservato per
comprenderne il
funzionamento
usiamolo per misurare
angoli dati o
disegnarne di nuovi.
Per rinforzare le conoscenze proponiamo alcune prove Invalsi da svolgere individualmente.
14 Il percorso in campo geometrico può continuare utilizzando la misura degli angoli nella
costruzione di triangoli e quadrilateri. Attraverso la misura degli angoli possiamo classificare i
triangoli e i trapezi; i bambini scoprono alcune relazioni sugli angoli interni (somma degli angoli
interni di un triangolo 180°, di un quadrilatero 360°, …)
15 Iniziamo una riflessione che sposta l’attenzione in ambito numerico
PERCHÉ GLI ANTICHI DECISERO DI DIVIDERE IL CERCHIO IN (30X12) 360 PARTI?
La risposta va cercata nelle proprietà dei numeri 12 e 30.
Il 12 e il 30 sono due numeri molto particolari perché si possono dividere in tanti modi senza
lasciare resto
Chiediamo individualmente di scrivere i divisori di 12, 30.
Collettivamente cerchiamo i divisori del 360 (in tutto sono 24)
Lavoriamo adesso su numeri con una quantità gestibile di divisori e riflettiamo e scriviamo tutte le
regole che i bambini riescono a trovare
Se è pari è divisibile per 2
Se è divisibile due volte per 2 è divisibile per 4
Se finisce per 0 o 5 è divisibile per 5
Se finisce per 0 è divisibile per 2, 5, 10
…
Colleghiamo le conoscenze sui divisori a quelle sui multipli
È NECESSARIO SVILUPPARE LE CONOSCENZE SU DIVISORI E MULTIPLI ALL’INTERNO DI
ATTIVITÀ SPECIFICHE SUL CALCOLO MENTALE PER FARE E APPLICARE NUOVE
SCOPERTE
Esempio:
Se un numero è divisibile per 2 e 3 è divisibile anche per 6 (in generale un numero divisibile per
due numeri è divisibile anche per il loro prodotto)
Un numero divisibile per un numero è divisibile anche per il risultato della divisione (es 48:4=12; 4
e 12 sono divisori di 48)
14. Come si misurano gli ANGOLI? Introducete questo argomento leggendo e commentando
insieme il testo inserito nel file allegato dal titolo : MISURA ANGOLO ( forse dovremmo trovare
qualcosa di più semplice). Presentate, quindi, il goniometro, osservatelo attentamente con i ragazzi
facendo loro notare in quante parti è diviso e sottolineando che ogni parte è un piccolissimo angolo
che si chiama ANGOLO GRADO ed è l’unità di misura convenzionale degli angoli. Date ai bambini
l’opportunità di usare più volte il goniometro per disegnare angoli di varie ampiezze e\o misurare
angoli di diverse ampiezze. Può darsi che alcuni alunni presentino significative difficoltà
nell’imparare ad usare questo strumento necessitando della guida sistematica dell’insegnante e\o
di compagni più esperti per misurare e disegnare angoli di ampiezza determinata. Lasciateli
provare e riprovare senza stupirvi dei loro errori. Potete anche far giocare i bambini ad ipotizzare
l’ampiezza degli angoli più “strani” ( piatto, giro, nullo) e poi procedere alla loro misurazione con il
goniometro.
15. Consegnate una nuova scheda di sintesi che raccolga tutti gli angoli fino ad ora scoperti e le
loro misure.
16. Riproponete ai bambini immagini e disegni di case costruite su terreno pianeggiante e su
terreno collinare. Fatele disegnare sul quaderno colorando di rosso le linee rette che
rappresentano i muri delle case, così:
Chiedete ai ragazzi di rispondere per scritto, individualmente, al seguente quesito: In entrambi i
disegni le linee verticali (di colore rosso) incontrano la linea del terreno (di colore verde). Qali
differenze noti nell’incidenza delle linee? La lettura delle risposte individuali e la successiva
discussione condurranno tutti gli alunni a capire che:
LE LINEE VERTICALI CHE RAPPRESENTANO I MURI DELLE CASE INCONTRANO LA
LINEA ORIZZONTALE DEL TERRENO PIANEGGIANTE FORMANDO ANGOLI RETTI.
LE LINEE VERTICALI CHE RAPPRESENTANO I MURI DELLE CASE INCONTRANO LA
LINEA OBLIQUA DEL TERRENO DELLA MONTAGNA FORMANDO 1 ANGOLO ACUTO
E UN ANGOLO OTTUSO.
17. Proponete ai ragazzi( muniti di blocco note e matita per appunti e disegni), un giro nell’edificio
scolastico e un’uscita nel giardino della scuola o in paese, alla scoperta di angoli retti. Al rientro in
classe stimolate una discussione collettiva su quanto osservato. I ragazzi riporteranno di aver
notato che la maggior parte degli angoli retti notati nell’ambiente sono formati dall’incontro di linee
verticali e orizzontali proprio come accade nell’incidenza delle linee verticali che rappresentano i
muri delle case con la linea che rappresenta il terreno pianeggiante. Tuttavia nei disegni di alcuni
cancelli, ringhiere e inferriate i ragazzi potranno scoprire la presenza di angoli retti determinati
dall’incontro di linee oblique. Dopo le esperienze e le riflessioni descritte sopra, si può proporre la
seguente sintesi:
18. Procedete proponendo agli alunni di disegnare linee perpendicolari su fogli quadrettati e fogli
bianchi . La difficoltà nel disegnare linee perpendicolari su fogli bianchii sarà subito
evidente,proponete, quindi, l’uso di riga e squadra invitando i ragazzi anche al prolungamento delle
linee perpendicolari per dare loro l’opportunità di scoprire che gli angoli retti che si formano dalla
loro incidenza sono 4.











