Dispensa sui numeri naturali

I NUMERI NATURALI
N={0, 1,2, 3, 4, …... }
PER MARTEDI' 22 SETTEMBRE:
• STUDIARE I PRIMI 6 PUNTI DI QUESTA DISPENSA
• RICOPIARE SUL QUADERNO LE PRIME DUE TABELLE
DEGLI ESERCIZI DELLA 3a PAGINA E COMPLETARLE
Nello studiare i numeri naturali provate a dimenticare gli altri numeri che
avete imparato (numeri con la virgola, numeri con il segno, frazioni ecc.)
e concentratevi solo sui naturali
1. Proprietà
•
•
•
•
•
•
•
Hanno un primo elemento, il numero 0
Non hanno ultimo elemento
Sono infiniti
Si possono ordinare
Ogni numero naturale ha un successivo
Ogni numeri naturale, escluso lo 0, ha un precedente
Si possono rappresentare su una semiretta
2. Operazioni
I numeri che compaiono in un'operazione sono chiamati in generale operandi
• Addizione: 2+5
• Moltiplicazione: 2⋅5
• Sottrazione: 5−2
• Divisione: 8 :2
• Elevamento a potenza: 25
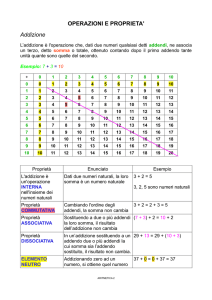
3. Addizione
Gli operandi vengono chiamati addendi ed il risultato somma
L'addizione da sempre come risultato un numero naturale: si dice che è un'operazione INTERNA ai
naturali
L'addizione gode della proprietà commutativa: 5+2=2+5
Lo 0 è detto elemento neutro dell'addizione perché aggiungere 0 ad un numero dà come risultato il
numero stesso
4. Moltiplicazione
•
Gli operandi che vengono chiamati fattori ed il risultato prodotto
•
•
•
La moltiplicazione dà sempre come risultato un numero naturale: si dice che è un'operazione
INTERNA ai naturali
L'addizione gode della proprietà commutativa: 5⋅2=2⋅5
Il numero 1 è chiamato elemento neutro della moltiplicazione perché moltiplicando per 1 un
numero dà come risultato il numero stesso
5. Sottrazione
•
•
•
Gli operando vengono chiamati: il primo minuendo, il secondo sottraendo ed il risultato
differenza. Esempio: 5-2=3 Quindi 5 è il minuendo, 2 il sottraendo, 3 è la differenza
Non si può sempre fare: 5−9 non dà come risultato un numero naturale, si dice che
l'operazione 5−9 è impossibile in N.
Non gode della proprietà communativa 5−3≠3−5
6. Divisione
•
•
•
•
•
Gli operandi vengono chiamati: il primo dividendo, il secondo divisore ed il risultato
quoziente
8 :2=4 Quindi 8 è il dividendo, 2 è il divisore e 4 è il quoziente
Non gode della proprietà communtativa 8 :2≠2 : 8
non si può dividere per 0
Se il risultato della divisione è un numero naturale si dice che la divisione è ESATTA e che
il dividendo è MULTIPLO del divisore.
Esempio: si può fare la divisione esatta 8:2 perché da come risultato il numero naturale 4 .
Si dice allora che che 8 è MULTIPLO di 2 oppure che 8 è divisible per 2. Si dice anche che
2 è divisore di 8 oppure che 2 è sottomultiplo di 8
Se il risultato della divisione non è un numero naturale, cioè non è possibile fare la divisione
esatta, allora si può eseguire la divisione EUCLIDEA o CON RESTO nel senso che si trova
un quoziente ed un resto
Esempio: Non si può fare la divisione esatta 5:3 ma si può eseguire la divisione euclidea che
fornisce come quoziente il numero 1 e come resto il numero 2
7. Elevamento a potenza
•
•
•
•
•
•
Es: 25 . Il numero 2 è chiamato base, il numero 5 esponente
L'elevamento a potenza non si può fare solo in un solo caso: 00
Se l'esponente è uguale a 0 allora il risultato è sempre 1. Es. 20=1
Se l'esponente è 1 allora il risultato è sempre la base. Es. 21=2
Se l'esponente è maggiore di 1, la potenza a n indica l'espressione a⋅a⋅a …⋅a con a
ripetuto n volte
Es: 25 significa 2⋅2⋅2⋅2⋅2 (2 è ripetuto 5 volte)
L'elevamento a potenza gode di alcune notevoli proprietà. Indichiamo il numero della base con le
lettere a, b ed il numero dell'esponente con le lettere n, m
n m
n+ m
•
a ⋅a =a
n
m
n−m
•
(con n≥m )
a :a =a
n m
n⋅m
•
(a ) =a
•
a n⋅bn =( a⋅b)n
•
a n :b n=(a : b)n
8. Espressione numerica
Si chiama espressione numerica una sequenza operazioni racchiuse eventualmente da parentesi
Es. 5+(5−2):3−4
Nel calcolare il valore di una espressione bisogna rispettare alcune regole:
• Le operazioni dentro le parentesi vanno svolte per prime
• Le operazioni vanno svolte in questo ordine: dapprima le potenze, poi le moltiplicazioni e
divisioni nell'ordine in cui si presentanto, infine le addizioni e sottrazioni nell'ordine in cui si
presentano.
9. Numeri primi e composti
Un numero naturale maggiore di 1 è detto primo se è divisibile per il numero 1 ed il numero stesso.
Se non è primo è detto composto
Un numero composto può essere scritto come un prodotto di numeri primi cioè può essere
scomposto in fattori primi
Es. 12=2⋅2⋅3=22⋅3
ESERCIZI
COMPLETARE
a
Successivo di a
Precedente di a
2
7
3
1
5
13
10
100
0
1
COMPLETARE
a
4
10
12
5
3
0
32
3
13
5
0
0
a≥b
a>b
b
no
no
a≤b
a<b
si
si
a
b
a è multiplo di b
b è multiplo di a
4
32
no
si
35
1
10
2
3
13
7
6
1
3
9
13
CALCOLA LE SEGUENTI POTENZE SCRIVENDO IL RISULTATO SOTTO FORMA DI
POTENZA
5 
0 
2
( 22 ) = 24
7 
6 6

2   

 1



 
3

3 4

3  
2
3 2
3
4 2
2 1
2
2 1

 0




10 
5 2
13 
7 6
1
2 0
6 7
4   


 2


  
4
3 3

13 

0

6   
5
3 0

 
4
3 2
3 

3
0 7



2
 10 2 3 1  




CALCOLA IL VALORE DELLE ESPRESSIONI UTILIZZANDO, SE POSSIBLE, LE
PROPRIETA' SULLE POTENZE
34  37 
23  25 
24⋅23
79  70 
510  58  53 
33  30  33 
9 2  95 
32  3  33  
52  55 
10 2  107  10 
7  7 3  71  7 2 
7  7 3  7   7 
32  3  32 
72  22  23
5   5 
0
54  52  52  5 
2
6 0
3 1

CALCOLA IL VALORE DELLE ESPRESSIONI UTILIZZANDO, SE POSSIBLE, LE
PROPRIETA' SULLE POTENZE
94 : 93 
12 5 : 12 0 
26 : 24 : 2 
5
10
: 55  : 52 : 5 
2
6
43 : 4 
157 : 33 
310 : 38 : 33  
27 : 23  22 
310 : 35 
618 : 6 9 : 61 
510 : 55 : 52 : 5 
510 : 55  52 : 5 
213 : 2 8 
1115 : 113 : 115 
38 : 34  : 33 : 3 
5  53  54 : 52   5
3