esercizi-vettori-forze

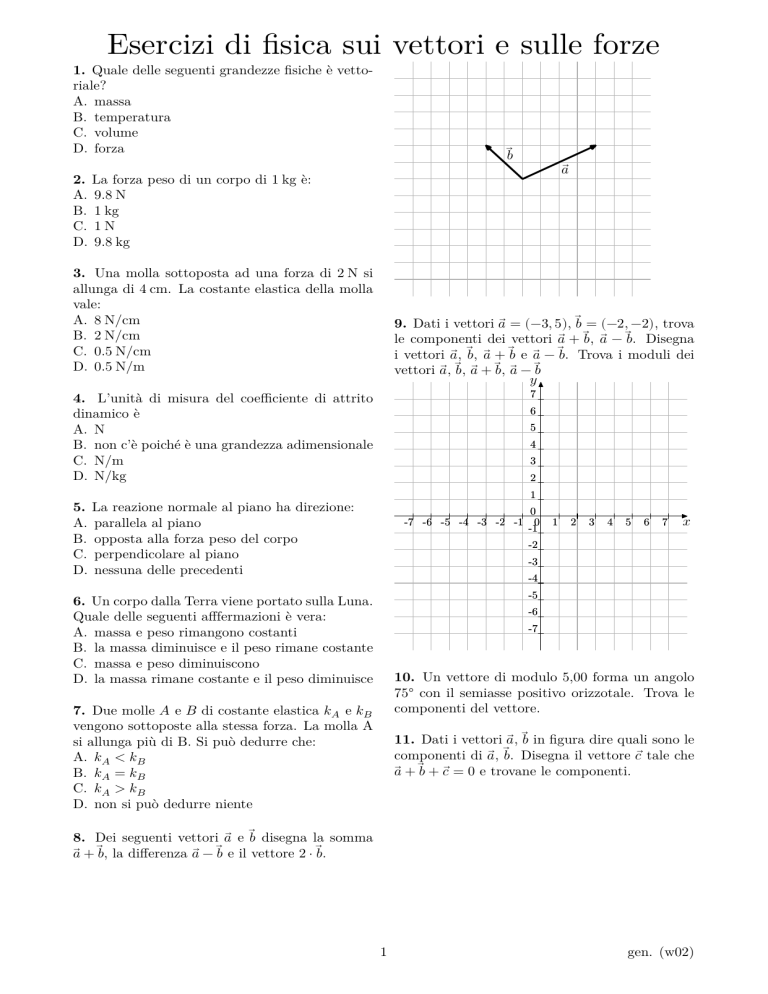
Esercizi di fisica sui vettori e sulle forze
1. Quale delle seguenti grandezze fisiche è vettoriale?
A. massa
B. temperatura
C. volume
D. forza
𝑏⃗
𝑎⃗
2. La forza peso di un corpo di 1 kg è:
A. 9.8 N
B. 1 kg
C. 1 N
D. 9.8 kg
3. Una molla sottoposta ad una forza di 2 N si
allunga di 4 cm. La costante elastica della molla
vale:
A. 8 N/cm
B. 2 N/cm
C. 0.5 N/cm
D. 0.5 N/m
9. Dati i vettori 𝑎⃗ = (−3, 5), 𝑏⃗ = (−2, −2), trova
le componenti dei vettori 𝑎⃗ + 𝑏,⃗ 𝑎⃗ − 𝑏.⃗ Disegna
i vettori 𝑎,⃗ 𝑏,⃗ 𝑎⃗ + 𝑏⃗ e 𝑎⃗ − 𝑏.⃗ Trova i moduli dei
vettori 𝑎,⃗ 𝑏,⃗ 𝑎⃗ + 𝑏,⃗ 𝑎⃗ − 𝑏⃗
𝑦
7
4. L’unità di misura del coefficiente di attrito
dinamico è
A. N
B. non c’è poiché è una grandezza adimensionale
C. N/m
D. N/kg
6
5
4
3
2
1
5. La reazione normale al piano ha direzione:
A. parallela al piano
B. opposta alla forza peso del corpo
C. perpendicolare al piano
D. nessuna delle precedenti
0
-7 -6 -5 -4 -3 -2 -1 0
-1
1
2
3
4
5
6
7
𝑥
-2
-3
-4
-5
6. Un corpo dalla Terra viene portato sulla Luna.
Quale delle seguenti afffermazioni è vera:
A. massa e peso rimangono costanti
B. la massa diminuisce e il peso rimane costante
C. massa e peso diminuiscono
D. la massa rimane costante e il peso diminuisce
-6
-7
10. Un vettore di modulo 5,00 forma un angolo
75° con il semiasse positivo orizzotale. Trova le
componenti del vettore.
7. Due molle 𝐴 e 𝐵 di costante elastica 𝑘𝐴 e 𝑘𝐵
vengono sottoposte alla stessa forza. La molla A
si allunga più di B. Si può dedurre che:
A. 𝑘𝐴 < 𝑘𝐵
B. 𝑘𝐴 = 𝑘𝐵
C. 𝑘𝐴 > 𝑘𝐵
D. non si può dedurre niente
11. Dati i vettori 𝑎,⃗ 𝑏⃗ in figura dire quali sono le
componenti di 𝑎,⃗ 𝑏.⃗ Disegna il vettore 𝑐 ⃗ tale che
𝑎⃗ + 𝑏⃗ + 𝑐 ⃗ = 0 e trovane le componenti.
8. Dei seguenti vettori 𝑎⃗ e 𝑏⃗ disegna la somma
𝑎⃗ + 𝑏,⃗ la differenza 𝑎⃗ − 𝑏⃗ e il vettore 2 ⋅ 𝑏.⃗
1
gen. (w02)
𝑦
7
6
5
4
3
2
1
𝑎⃗
0
-7 -6 -5 -4 -3 -2 -1 0
-1
𝑏⃗
1
2
3
4
5
6
7
𝑥
-2
-3
-4
-5
-6
-7
12. Due forze di modulo 10 N e 15 N hanno
stessa direzione e verso opposto. Fai un disegno
in scala delle due forze, disegna la somma delle
due forze e calcolane il modulo.
13. In figura è mostrata la forza elastica di una
molla in funzione dell’allungamento. Trova la
forza corrispondente all’allungamento di 5 cm e
trova la costante elastica della molla.
𝐹 (𝑁 )
45
40
35
30
25
20
15
10
5
1
2
3
4
5
6
7
8
9 𝑠(𝑐𝑚)
2
gen. (w02)
Soluzioni.
Soluzione 1
D
Soluzione 2
A
Soluzione 3
C
Soluzione 4
B
Soluzione 5
C
Soluzione 6
D
Soluzione 7
A
Soluzione 8
Soluzioni in rosso, vettori per la costruzione in grigio.
2𝑏⃗
𝑎 ⃗ + 𝑏⃗
𝑏⃗
𝑎⃗
𝑎 ⃗ − 𝑏⃗
Soluzione 9
𝑎⃗ + 𝑏⃗ = (−5, 3), 𝑎⃗ − 𝑏⃗ = (−1, 7). √
√
|𝑎|⃗ = √(−3)2 + 52 = 9 + 25 = 34 = 5.83,
√
√
|𝑏|⃗ = √(−2)2 + (−2)2 = 4 + 4 = √
8 = 2.83
√
2
2
⃗
|𝑎⃗ + 𝑏| = √(−5) + 3 = 25 + 9 = 34 = 5.83
√
√
|𝑎⃗ − 𝑏|⃗ = √(−1)2 + 72 = 1 + 49 = 50 = 7.07
3
gen. (w02)
𝑦
𝑎 ⃗ − 𝑏⃗
𝑎⃗
7
6
5
4
𝑎 ⃗ + 𝑏⃗
3
2
1
0
-7 -6 -5 -4 -3 -2 -1 0
-1
1
3
2
4
5
6
7
𝑥
-2
𝑏⃗
-3
-4
-5
-6
-7
Soluzione 10
𝑣𝑥 = 5,00 ⋅ cos 75° = 1,29
𝑣𝑦 = 5,00 ⋅ sin 75° = 4,83
Soluzione 11
𝑎⃗ = (−3, 0)
𝑏⃗ = (1, 3)
𝑐 ⃗ = −(𝑎⃗ + 𝑏)⃗ = (2, −3)
𝑦
7
6
5
4
3
2
1
𝑎⃗
0
-7 -6 -5 -4 -3 -2 -1 0
-1
𝑏⃗
1
3
2
4
5
6
7
𝑥
-2
-3
-4
𝑐⃗
-5
-6
-7
Soluzione 12
⃗ | = |𝐹1⃗ + 𝐹2⃗ | = 5𝑁
|𝐹𝑡𝑜𝑡
𝐹2⃗
Soluzione 13
𝐹1⃗
⃗
𝐹𝑡𝑜𝑡
𝐹 (5cm) = 15 N
𝑘 = 3 N/cm = 300N/m
4
gen. (w02)