caricato da
common.user18086
Statistica: Definizioni, Caratteri e Distribuzioni

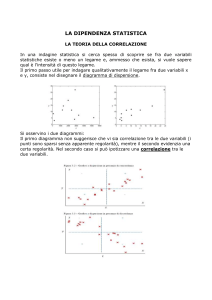
Definizione di statistica La statistica è una disciplina che studia fenomeni collettivi in termini quantitativi. I fenomeni collettivi sono fenomeni il cui studio richiede l’osservazione di un insieme di manifestazioni individuali (ad esempio altezza di un gruppo, consumo di un determinato bene, reddito, ecc.) “La Statistica è la disciplina che elabora i principi e le metodologie che presiedono al processo di rilevazione e raccolta dei dati, alla rappresentazione sintetica e alla interpretazione dei dati stessi e, laddove ve ne siano le condizioni, alla generalizzazione delle evidenze osservate” (Cicchitelli, 2012). Unità statistiche e collettivi statistici Le unità statistiche sono le unità elementari (ui, i=1,…N) di questa disciplina e rappresentano i casi individuali che sono oggetto di osservazione (ad esempio se si vuole descrivere l’andamento accademico di una classe di un corso di laurea, i singoli studenti rappresentano le unità statistiche). Ci sono unità statistiche semplici e complesse: Le unità statistiche semplici: sono quelle che rappresentano un solo elemento, ad esempio una singola persona. Le unità statistiche complesse: sono quelle che rappresentano più elementi, ad esempio una famiglia, un’azienda turistica. L’insieme di più unità statistiche omogenee rispetto ad una o più caratteristiche costituisce un collettivo statistico o popolazione. Il numero delle unità statistiche di un collettivo costituisce la numerosità del collettivo che viene indicata con N. I collettivi possono essere: Finiti: sono costituiti da un numero finito di unità statistiche; Infiniti: sono costituiti da un numero infinito di unità statistiche. I collettivi finiti sono concreti, quelli infiniti sono ipotetici. Caratteri e modalità I caratteri sono le caratteristiche del collettivo statistico (ad esempio l’età, il sesso, la professione, il titolo di studio, il reddito, ecc.). Le modalità del carattere sono le caratteristiche assunte da ogni singola unità statistica del collettivo. Esempio riassuntivo Giorgio Camilla Età 37 20 Giordana 26 Nicolò 23 Sesso Titolo di studio M Laurea F Diploma Attività Occupato Disoccupato Peso 70kg 53kg F M Occupato Studente 50kg 67kg Laurea Diploma Giorgio, Camilla, Giordana, Nicolo sono le unita statistiche; L’insieme degli individui [Giorgio, Camilla, Giordana, Nicolo] = popolazione (collettivo); Età, Sesso, Titolo di studio, Attività, Peso sono i caratteri; 37…23; M…M; Laurea…Diploma; Occupato…Studente; 70…67 sono le modalità dei caratteri. Un carattere può assumere modalità differenti in corrispondenza delle diverse unità statistiche del collettivo. È importante che le modalità di un carattere siano: Esaustive, ossia devono rappresentare tutti i possibili modi di essere del carattere (ad esempio nel caso del carattere Sesso, le modalità possono essere Maschio, Femmina e Altro). Non sovrapposte, ossia ad ogni unità statistica si può associare una sola modalità del carattere. Tipi di caratteri Caratteri qualitativi (mutabili statistiche): le modalità sono costituite da espressioni verbali (ad esempio sesso, professione, stato civile, ecc.). Caratteri quantitativi (variabili statistiche): le modalità sono costituite da numeri (ad esempio età, peso, numero di figli, ecc.). Misurazione dei caratteri qualitativi I caratteri qualitativi possono classificarsi in: Caratteri sconnessi (o con scala nominale): quando non presentano un ordine naturale; ossia se date due sue modalità è possibile solo affermare se queste sono uguali o diverse (sesso, luogo di nascita). Essi si distinguono a loro volta in: Caratteri sconnessi dicotomici quando possono assumere 2 sole modalità, convenzionalmente indicate con 0 e 1. (ad esempio, l’esito di un concorso presenta due sole modalità: “superato” o “non superato”). Caratteri sconnessi politomici quando assumono un numero finito di modalità distinte (ad esempio, il colore delle auto presenti una concessionaria perché assume un numero di modalità superiore a 2: grigio, nero, blu, rosso, ecc.). Caratteri ordinati (o con scala ordinale), quando le modalità presentano un ordine naturale, ossia se date 2 sue modalità è possibile solo dare un ordine, specificando che una precede l’altra (ad esempio, grado di soddisfazione – poco, abbastanza, molto – posizione in graduatoria, titolo di studio. Essi si distinguono a loro volta in: Caratteri ordinati rettilinei: se possiedono una modalità iniziale e una finale (pochissimo, poco, abbastanza, molto, moltissimo). Caratteri ordinati ciclici: se non hanno vere e proprie modalità iniziali e finali (sono fissate solo in modo convenzionale) (mese di nascita, direzione del vento - Nord Sud Ovest Est). Misurazione dei caratteri quantitativi I caratteri quantitativi possono classificarsi in: Caratteri discreti: quando l’insieme delle modalità può essere messo in corrispondenza biunivoca con un sottoinsieme dei numeri interi. (numero di figli, numero di posti letto in un ospedale; i numeri interi sono quelli senza la virgola). Caratteri continui: quando invece l’insieme delle modalità può essere messo in corrispondenza biunivoca con un sottoinsieme dei numeri reali. (peso o statura di un individuo; i numeri reali sono quelli con la virgola). Trasferibilità del carattere Un carattere è trasferibile se ha senso immaginare che un’unità statistica possa cedere tutto o parte del carattere posseduto ad un’altra unità statistica. Viceversa, si parla di carattere non trasferibile. Suddivisione in classi del carattere In alcune situazioni e opportuno effettuare alcune trasformazioni dei caratteri. Quando il carattere che si vuole analizzare presenta un numero eccessivo di modalità distinte, si possono avere notevoli difficolta nella comprensione dei dati osservati. In tali casi può essere necessario procedere ad un accorpamento delle modalità. Se il carattere e quantitativo si definisce suddivisione in classi del carattere l’operazione consistente nella suddivisione dell’insieme dei possibili valori in intervalli tra loro disgiunti. Distribuzioni unitarie o distribuzioni statistiche disaggregate Definiamo Distribuzione unitaria semplice (o distribuzione statistica semplice disaggregata o serie di osservazioni) di un solo carattere, l’elencazione delle modalità osservate, unità per unità, nel collettivo in esame. Unità U1 Carattere X1 ∶ ∶ Ui Xi ∶ ∶ UN XN Unità 1 2 3 4 5 6 7 8 Carattere M F F M M F M F Parliamo di Distribuzione unitaria multipla (o distribuzione statistica multipla disaggregata) quando consideriamo più caratteri. Giorgio Camilla Età 37 20 Giordana 26 Nicolò 23 Sesso Titolo di studio M Laurea F Diploma Attività Occupato Disoccupato Peso 70kg 53kg F M Occupato Studente 50kg 67kg Laurea Diploma Distribuzioni di frequenze Le unità o le osservazioni della distribuzione disaggregata vengono generalmente classificate e aggregate in gruppi omogenei sulla base di uno o più caratteri. La scelta delle modalità è condizionata dal livello di disaggregazione con cui i dati sono stati rilevati. L’aggregazione comporta sempre una perdita di informazioni. Rispetto alla distribuzione unitaria semplice, per ottenere una maggiore sintesi occorre considerare la frequenza con cui le diverse modalità sono state osservate. La frequenza è il numero di volte che una determinata modalità si verifica nel collettivo di riferimento: Quando la frequenza è un numero intero non negativo si parla di frequenza assoluta; Quando la frequenza assoluta è rapportata al totale delle unità statistiche della popolazione si parla di frequenza relativa; Quando la frequenza assoluta è rapportata al totale delle unità statistiche della popolazione e moltiplicata per 100 si parla di frequenza percentuale. Dunque, una rappresentazione più sintetica dei dati si può avere attraverso la distribuzione di frequenze. Una distribuzione di frequenze è un’organizzazione dei dati in forma tabellare tale che ad ogni modalità di una certa variabile (quantitativa o qualitativa) si fa corrispondere la rispettiva frequenza (assoluta o relativa). Si dice distribuzione di frequenze semplice, se si riferisce ad 1 carattere, invece si dice multipla, se si riferisce a più caratteri. Nel caso di modalità raggruppate in classi di valori si possono distinguere i seguenti casi (indichiamo gli estremi inferiori e superiori delle k classi in cui è suddiviso il carattere continuo X rispettivamente con ci-1, i=1, …, K): 1. Classe aperta a destra e chiusa a sinistra: ci-1 |- ci. Tali classi comprendono il valor xi e non il valore xi+1. 2. Classe aperta a sinistra e chiusa a destra: ci-1 -| ci. Tali classi comprendono il valor xi+1 e non il valore xi. A volte quando il campo di esistenza dei valori di xi è molto ampio e si hanno diramazioni di valori agli estremi si considerano classi estreme aperte (ci-1 - ci). In altri casi si possono considerano classi estreme chiuse in entrambi gli estremi (ci-1 |--| ci). Definiamo ampiezza della generica classe ci-1 - ci la differenza tra l’estremo destro ed estremo sinistro, e valore centrale la somma degli estremi della classe divisi per due [ci-1 - ci/2]. Parliamo di frequenze cumulate associate ad una modalità del carattere la frequenza che misura il numero di casi che presentano un valore non superiore a quella modalità. Questo tipo di frequenza può essere calcolata tramite le frequenze assolute, relative e percentuali. La densità di frequenza di una classe generica ci-1 - ci di una distribuzione di frequenze con modalità raggruppate in classi è il rapporto tra la frequenza della classe e l’ampiezza della classe. Rappresentazione grafica dei dati statistici L’istogramma Box plot Grafico a torta Istogrammi con classi di diversa ampiezza Distribuzione di frequenza Variabili statistiche doppie Supponiamo che la variabile X assuma le k modalità distinte: x1, x2, …, xk e che la variabile Y assuma le h modalità y1, y2, …, yh. Si utilizza una tabella a doppia entrata come la seguente per rappresentare le rispettive frequenze assolute. Data questa distribuzione di una variabile doppia (X, Y) si possono derivare: Distribuzioni marginali della X e della Y Distribuzioni condizionate di Y dato un certo valore di X ( Y | X = x ) e viceversa ( X | Y = y ) Esempio Nel corso di un anno su 1000 pazienti ricoverati presso una struttura ospedaliera sono state osservate le variabili: X= numero di episodi critici giornalieri registrati Y= giorni di degenza 40 pazienti hanno presentato 3 (variabile X) episodi critici durante un ricovero durato 3 giorni (variabile Y). Per le distribuzioni marginali e condizionate è possibile calcolare tutte le usuali statistiche descrittive (indici sintetici). Legame tra variabili qualitative Il legame tra le componenti di una variabile doppia può essere studiato mediante indici basati soltanto sulle frequenze (indici di connessione) o attraverso misure basate sulle modalità quantitative (misure di correlazione). Gli indici di connessione sono utilizzabili solo per lo studio di variabili qualitative doppie, mentre nel caso di due variabili quantitative è possibile utilizzare sia gli indici di connessione che le misure di correlazione. Nel legame tra variabili al variare dei valori assunti da una variabile X non si modifica la distribuzione di frequenza della variabile Y (o viceversa, se valore al variare dei valori assunti da Y non si modifica la distribuzione di frequenza della variabile X) si parla di Indipendenza tra variabili. L’indipendenza implica che la conoscenza di un valore di una delle due variabili non aggiunge alcuna informazione alla conoscenza dell’altra. Il legame tra le variabili può essere misurato attraverso la “distanza” tra le frequenze doppie realmente osservate nella popolazione in esame e le frequenze ipotetiche che si osserverebbero nel caso di indipendenza. Maggiore la distanza, maggiore il legame tra le due variabili considerate, minore la distanza, minore sarà il legame tra le due variabili considerate. Le componenti X e Y di una variabile doppia (X, Y) si dicono indipendenti se e solo se le distribuzioni di frequenza relative e condizionate di X e di Y sono costanti ovvero sono uguali tra loro e uguali alla distribuzione marginale. Quindi per ogni valore di xi, avremo: Similmente per ogni valore di yi, avremo: Le componenti X e Y di una variabile doppia (X, Y) sono indipendenti se e solo se, per ogni coppia di modalità (xi, yi) tutte le frequenze doppie (mij) e marginali (ni. e n.j) sono legate da una relazione di proporzionalità cioè se per tutti i valori di i e j si ha: Da cui: Queste sono le cd frequenze teoriche quelle che osserveremmo nella tabella se X ed Y fossero indipendenti. *approfondire questo argomento con la slide numero 8* Legame tra due variabili quantitative Nel caso in cui le componenti della variabile doppia (X, Y) siano ambedue variabili quantitative, per misurare il legame tra X e Y si utilizza, preferibilmente, un indice che coinvolge anche le modalità numeriche, ovvero il coefficiente di correlazione lineare. Questo coefficiente misura il legame di tipo lineare, cioè quello esprimibile mediante una relazione lineare tra le variabili X e Y. Una prima indicazione sull’esistenza di questo legame lineare la si può ottenere ispezionando lo scatterplot, ovvero la rappresentazione sugli assi cartesiani dove vengono riportate le n coppie di valori (xi, yi) relative alle due variabili. Come si può notare la nuvola dei punti indica che al crescere di X cresce anche la Y. Questo suggerisce che c’è un legame tra le due variabili e questo legame è lineare poiché la nuvola dei punti può essere ben approssimata dalla retta in blu cioè da una relazione del tipo y = ax+b. Grazie allo scatterplot si può anche comprendere il tipo di legame tra le due variabili, di tipo diretto, inverso oppure l’assenza di legame. La misura sintetica delle variazioni congiunte è fornita dal coefficiente di correlazione lineare di BravaisPearson: Consideriamo il numeratore dell’indice di correlazione: Se a scarti positivi di X (xi – ux) corrispondono prevalentemente scarti positivi di Y (yi – uy) e viceversa, se scarti negativi di X (xi – ux) corrispondono prevalentemente scarti negativi di Y (yi – uy), allora le variabili X e Y variano nella stessa direzione e il prodotto degli scarti è positivo; Invece, se a scarti positivi di X corrispondono prevalentemente a scarti negativi di Y e viceversa, le variabili X e Y variano in direzione opposta: prodotto degli scarti è negativo; Il numeratore preso singolare mente è esso stesso un indicatore del legame tra X e Y che prende il nome di covarianza, ed esprime come variano congiuntamente X e Y in rapporto alle rispettive medie; Il segno del coefficiente di correlazione dipende proprio dal segno della covarianza poiché il denominatore del rapporto che definisce il coefficiente di correlazione è sempre positivo. Proprietà del coefficiente di correlazione lineare: 1) Corr(X, Y) = Corr(Y, X) 2) Corr(X, X) = 1 3) -1 ≤ Corr(X, Y) ≤ 1 4) Se X e Y indipendenti -> Corr(X, Y) = 0 Nella quarta proprietà della correlazione lineare tutte le relazioni di indipendenza tra X e Y sono pari a 0, ma non tutte le correlazioni pari a 0 sono indipendenti, perché la condizione di indipendenza richiede l’assenza di qualsiasi legame tra X e Y (è cioè impossibile dedurre informazioni su Y conoscendo il valore di X, e viceversa). Invece la correlazione nulla significa che solo tra X e Y non vi è un legame di tipo lineare, ma non consente di escludere la sussistenza di legami di natura diversa (ad esempio legame quadratico). Il segno del coefficiente. Nell’interpretazione va considerata la direzione del legame lineare espressa dal segno positivo (relazione diretta) o negativo (relazione inversa). Rispetto alla retta ideale che attraversa la nuvola dei punti delle osservazioni il segno esprime se la retta avrà pendenza positiva o negativa. Il valore del coefficiente. Questo esprime la forza del legame lineare, che può essere forte in senso positivo (prossimo ad 1) o in senso negativo (prossimo a -1). Il quadrato di Corr(X, Y). Questo rappresenta una misura dell’aderenza della nuvola dei punti alla retta ideale che la attraversa. Il coefficiente di correlazione lineare esprime anche il grado di prevedibilità di una variabile Y tramite un’altra X, grazie ad una funzione lineare Maggiore è il valore del coefficiente di correlazione al quadrato maggiore sarà la capacità di X di predire Y tramite una funzione lineare. Graficamente, maggiore è la aderenza dei punti alla retta maggiore sarò questa prevedibilità. Perciò è importante considerare la quantità [Corr(X, Y)]2.