caricato da
common.user14576
Meccanica Quantistica: Basi Sperimentali - Corpo Nero e Spettroscopia

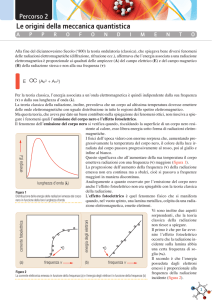
Capitolo 1 Le basi sperimentali della meccanica quantistica 1.1 Introduzione Dopo le intuizioni di Galileo e Newton, ci fu un lungo periodo di assestamento durante il quale si edificò l’intero corpo di ciò che oggi chiamiamo fisica classica, comprendente, in particolare, i principi della dinamica, sia nella forma di Newton che in quella, meno familiare per i chimici, di Hamilton, l’elettromagnetismo, l’ottica ondulatoria e la termodinamica. Questa solida base scientifica permetteva di razionalizzare tutti, o quasi, i fenomeni fisici noti all’epoca. La situazione cambiò radicalmente con i primi esperimenti riguardanti l’interazione luce-materia, effettuati a cavallo dei secoli XIX e XX: non solo la teoria non permetteva di razionalizzare le nuove osservazioni sperimentali, ma in alcuni casi conduceva a risultati inaccettabili. Tra i casi più emblematici c’è quello dello spettro di emissione di cavità radianti - il cosiddetto corpo nero. Se si riscalda un corpo qualsiasi questo emette radiazione elettromagnetica; nel caso in cui il corpo ha forma di una piccola cavità – si pensi al piccolo foro di osservazione di una fornace per la cottura della terracotta o più semplicemente al forno di un pizzaiolo con un’apertura infinitamente piccola – la radiazione emessa ha due importanti proprietà: i) non dipende dal materiale che costituisce la cavità; ii) dipende significativamente dalla temperatura. Ad alte temperature la radiazione emessa cade nella regione del visibile (come accade ad esempio al sottile filo di tungsteno riscaldato ad alte temperature per effetto Ohm nelle normali lampadine ad incadescenza), mentre a temperature 1 2CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA più basse la radiazione cade prevalentemente nella regione dell’infrarosso. La termodinamica e l’elettrodinamica classica non solo erano incapaci di spiegare in che modo lo spettro di una cavità radiante variasse con la temperatura e la frequenza, ma addirittura conducevano a risultati fisicamente inaccettabili, secondo i quali l’intensità e quindi l’energia della radiazione tendeva all’infinito all’aumentare della frequenza, la cosiddetta catastrofe ultravioletta. Questo fenomeno e molti altri potevano essere spiegati solo a patto di introdurre un principio del tutto nuovo: l’esistenza di stati microscopici discreti, con valori ben determinati di alcune grandezze fisiche, quali ad esempio l’energia ed il momento angolare. La maggior parte di questi nuovi fenomeni erano connessi a processi di interazione radiazione-materia, ma in alcuni casi essi riguardavano interazioni tra corpuscoli microscopici, in assenza di radiazione elettromagnetica, come nel caso dell’esperimento di Franck-Hertz. Altre osservazioni emblematiche, come ad esempio le figure di interferenza osservate bombardando con un fascio di elettroni un cristallo di nickel, potevano essere facilmente spiegate solo assumendo che un fascio di elettroni si comporta in certe condizioni come un fascio di radiazione elettromagnetica, seguendo le leggi dell’ottica ondulatoria. In certe altre condizioni, gli esperimenti mostrano che anche la radiazione elettromagnetica si comporta come un fascio di particelle (effetto Compton), segue cioè le leggi di conservazione dell’energia e della quantità di moto che si utilizzano per trattare la cinematica di particelle macroscopiche. In definitiva, le nuove osservazioni mostravano che in alcuni esperimenti risultava più conveniente utilizzare un approccio di tipo corpuscolare, mentre in altri risultava più efficace l’approccio ondulatorio, una dicotomia passata alla storia come ”dualismo” onda-materia. In realtà, man mano che la nuova teoria andava sviluppandosi, si osservò come essa fosse perfettamente conciliabile con le vecchie leggi della fisica classica, che ingloba completamente, e ne rappresentasse perciò il naturale ampliamento ai sistemi microscopici. Questo concetto rappresentò una tappa fondamentale nello sviluppo della nuova teoria, talmente importante da essere sancito in uno dei principi storicamente più importanti della meccanica quantistica, il principio di corrispondenza. In questo capitolo si mostrerà come per spiegare lo spettro del corpo nero Planck arrivò alla prima formulazione dell’esistenza di stati ad ener- 1.2. GRANDEZZE RADIOMETRICHE 3 gia discreta, i cosiddetti stati quantici, 1 e come Einstein, interpretando l’effetto fotoelettrico, introdusse la legge di proporzionalità tra frequenza della radiazione ed energia; due leggi che, fuse nei famosi postulati di Bohr, rappresentano i fondamenti della moderna spettroscopia. Si passerà poi all’analisi degli spettri atomici e da questi alla formulazione di Bohr dell’atomo di idrogeno con la prima ipotesi di quantizzazione del momento angolare. 1.2 Grandezze radiometriche Prima di affrontare lo studio del corpo nero, definiamo alcune grandezze di uso comune nello studio dell’interazione radiazione materia. L’intensità di una sorgente di radiazione elettromagnetica si ottiene misurando il flusso di energia in un certo intervallo di tempo dt: Φ= dE dt [ergs−1 ; W] Il flusso determinato ad ogni specifica frequenza o lunghezza d’onda, raccogliendo l’energia in un intervallino di frequenza ν−ν+δν o di lunghezza d’onda λ − λ + δλ, è chiamato flusso specifico di radiazione o flusso radiante spettrale: dEλ [ergs−1 cm−1 ; Wm−1 ] Φλ = dt . Per convertire Φν in Φλ e viceversa si sfrutta il principio di conservazione dell’energia nell’intervallo spettrale: Φν dν = −Φλ dλ. (1.1) Il segno meno è necessario in quanto un aumento di frequenza corrisponde ad una diminuzione di lunghezza d’onda e permette di avere sia Φν che Φλ positive. c −dλ = 2 Fλ (1.2) Φν = Φλ dν ν 1 Si osservi che il termine quantizzazione è improprio quando riferito all’energia, al suo posto andrebbe utilizzato il termine discretizzazione 4CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA Si definisce intensità radiante spettrale Iν o brillanza Bν il flusso radiante per unità di angolo solido: Iν = dΦν dΩ [Wsr−1 ] (1.3) Il simbolo sr indica lo steradiante, l’unità di misura dell’angolo solido. Lo si utilizza solo quando necessario in quanto si tratta di un numero puro, essendo definito, in analogia con il radiante, come il rapporto tra l’area della superficie sferica sottesa ad un cono di angolo solido dΩ ed il quadrato della distanza dal vertice del cono, si veda figura 1.1. Figura 1.1: Definizione di angolo solido Si definisce infine densità di radiazione uλ l’energia radiante per unità di volume. 1.3 Lo spettro del corpo nero Definiamo corpo nero un corpo che assorbe tutta la radiazione incidente senza rifletterne neanche una minima quantità. In parole piú tecniche, il 1.3. LO SPETTRO DEL CORPO NERO 5 corpo nero2 ha potere assorbente αν unitario a qualsiasi frequenza ν. Il corpo nero non esiste in natura ma si può realizzare con un semplice stratagemma: si consideri una cavità con pareti scabre e con un foro di uscita di superficie infinitesima rispetto alla superficie interna della cavità. La radiazione elettromagnetica entra atraverso il foro ed urta contro le pareti della cavità venendo in parte assorbita ed in parte riflessa. Indicando con α il coefficiente di assorbimento del materiale che costituisce le pareti della cavità e con I0 l’intensità della radiazione entrante, la frazione assorbita è, per definizione, Iass =I0 α e la frazione riflessa ovviamente I0 (1 − α). Considerando che le pareti della cavità sono scabre, il raggio sarà riflesso in una direzione diversa da quella di incidenza ed inciderà nuovamente sulle pareti della cavità, cambiando ad ogni urto la sua traiettoria, cosı̀ come illustrato in figura 1.2. Se il foro ha un’estensione superficiale piccola rispetto alle pareti della cavità saranno necessari molti urti prima che il raggio riflesso esca dalla cavità. Dopo il primo urto con le pareti della cavità, il raggio riflesso avrà intensità pari a I1 = I0 (1 − α) . Dopo n urti: In = I0 (1 − α)n . Anche se il coefficiente di assorbimento non è molto elevato, bastano relativamente pochi urti per far diminuire drasticamente l’intensità della luce incidente. Per α=0.3, un valore non molto elevato e facilmente ottenibile con i materiali presenti in natura per qualunque frequenza della luce incidente, dopo 50 urti l’intensità della luce incidente sulla superficie interna della cavità si è ridotta ad un centimilionesimo di quella iniziale, una quantità non più misurabile, per cui il coefficiente di assorbimento dell’intera cavità risulta unitario. Unicità del corpo nero Se opportunamente eccitato, ad esempio per via termica, il corpo nero emette radiazione elettromagnetica in un vasto intervallo di frequenza. Sperimentalmente si osserva che la radiazione emessa da una simile cavità è indipendente dalla forma e dimensione della cavità, cosı̀ come non dipende dal materiale che costituisce la cavità, ma dipende soltanto dalla temperatura. Questo comportamento apparentemente sor2 l’articolo determinativo è qui utilizzato in quanto esiste un unico (non un generico) corpo nero, le cui proprietà sono indipendenti dalla forma, dal materiale utilizzato, etc. 6CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA Figura 1.2: Cammino della radiazione all’interno del corpo nero prendente è in realtà una conseguenza del fatto che il coefficiente di assorbimento della cavità è unitario ed è facilmente spiegabile in base ai principi della termodinamica. Si consideri il seguente esperimento ideale. Due cavità diverse, sia per il materiale utilizzato che per forma, sono poste in due termostati alla stessa temperatura; il fascio di radiazione emesso dall’una è focalizzato sul forellino dell’altra e viceversa, ad esempio attraverso uno specchio ed un’opportuna lente, come mostrato in figura fig. 1.3. Se, per assurdo, l’intensità radiante emessa dal corpo 1 fosse maggiore dell’intensità radiante emessa dal corpo 2, allora la cavità 2 assorbirebbe più energia di quanta ne riesce ad emettere, riscaldandosi rispetto al corpo 1. Dopo un certo tempo il corpo 1 che emette più energia del 2 si raffredderebbe e ci sarebbe passaggio di energia da un corpo più freddo ad uno più caldo, ma ciò è vietato dal secondo principio della termodinamica. Ne consegue che la radiazione emessa dalla cavità, lo spettro del corpo nero,3 è indipendente dalla natura del materiale con cui è costruita la cavità e dipende solo dalla temperatura. Questo è un punto estremamente importante in quanto stabilisce che l’emissione specifica (l’emissione in un intervallino infinitesimo di frequenza ν − ν + dν) è una funzione universale dell’energia e della temperatura e come tale deve essere ricavabile da principi primi. 3 Lo spettro di una radiazione elettromagnetica è la funzione di distribuzione delle frequenze in essa contenute. 1.3. LO SPETTRO DEL CORPO NERO 7 Figura 1.3: Apparato sperimentale per la dimostrazione dell’unicità del corpo nero Lo spettro del corpo nero Lo spettro del corpo nero è mostrato in fig. 1.4; in condizioni di equilibrio termodinamico, quando cioè lo spettro della radiazione emessa dalla cavità non varia nel tempo, valgono le quattro leggi seguenti: • Per piccole frequenze l’intensità specifica di radiazione è proporzionale alla temperatura ed al quadrato della frequenza, Iν ∝ ν 2 T (legge di Rayleigh-Jeans); • per grandi frequenze l’intensità specifica di radiazione decade esponenzialmente al crescere della frequenza, Iν ∝ ν 3 exp (−ν/T ) (legge di Wien); • la frequenza a cui cade la massima emissione dipende linearmente dalla temperatura, νmax = cost × T (legge dello spostamento di Wien); • la potenza dell’emissione per unità di superficie è proporzionale alla quarta potenza della temperatura, W = σT 4 , legge di Stefan-Boltzmann, con σ =5.67 ×10−8 Wm−2 K−4 . In virtù dell’unicità del corpo nero, lo spettro della radiazione emessa dal corpo nero deve essere ottenibile da principi primi, quali ad esempio le tre leggi della termodinamica e le leggi dell’elettrodinamica classica. Malgrado i numerosi sforzi, non fu possibile ottenere una funzione che rispettasse tutte le osservazioni sperimentali. Dalla termodinamica è possibile ricavare con estrema facilità la legge di Stefan-Boltzmann, mentre dalle leggi dell’elettromagnetismo è possibile ottenere la legge di Rayleigh-Jeans. Tuttavia, 8CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA Figura 1.4: Lo spettro del corpo nero poiché in elettrodinamica classica l’energia della radiazione non dipende dalla frequenza, la fisica classica prevede che la legge di Rayleigh-Jeans deve valere sia alle basse che alle alte frequenze, in evidente contrasto con i risultati sperimentali. Consideriamo una cavità radiante all’equilibrio termico. In tali condizioni lo spettro emesso non varia nel tempo, un ipotetico osservatore vedrebbe le pareti interne della cavità brillare in modo uniforme, senza disomogeneità di colore. In queste condizioni, per ogni punto della cavità si ha uguaglianza tra potenza assorbita ad una certa frequenza e potenza emessa alla stessa frequenza. dWνass = dWνem . (1.4) Poiché la potenza assorbita è pari alla potenza incidente per il coefficiente di assorbimento, dWνass = αν dWνinc , (1.5) e dal momento che il coefficiente di assorbimento del corpo nero è unitario, la potenza emessa è proporzionale alla densità di radiazione all’interno della cavità, che come visto (par. 1.2) è proporzionale all’intensità specifica di 1.3. 9 LO SPETTRO DEL CORPO NERO radiazione Iν . La legge di Stefan-Boltzmann La radiazione presente nella cavità può essere trattata alla stregua di un gas, la cui pressione dipende dalla densità di energia (p = uν /3)4 . Dal primo principio della termodinamica: dU = dQ − pdV = T dS − pdV derivando rispetto al volume si ottiene: ∂U ∂S ∂p =T −p=T −p ∂V T ∂V T ∂T V (1.6) (1.7) Poiché ∂U ∂V = uν e p= T uν 3 (1.8) si ha: T uν = 3 ∂uν ∂T − uν , 3 (1.9) dalla quale, separando le variabili ed integrando si ottiene: dT duν =4 uν T (1.10) uν = cost × T 4 (1.11) La potenza emessa dal corpo nero non è altro che la densità specifica di radiazione presente nella cavità per unità di tempo (W=J/s) sommata su tutte le frequenze (vedi eq. (1.27)) e pertanto la relazione trovata precedentemente è proprio la legge di Stefan-Boltzmann. La legge di Rayleigh-Jeans Planck cercò di ottenere l’espressione di uν dalle leggi della elettrodinamica classica. È noto che una particella elettrica in movimento assorbe ed emette radiazione elettromagnetica. Se la particella viene posta in un campo di radiazione elettromagnetica di densità uν , essa assorbe energia pari a: dεass = 4 πe2 uν dt, 3m (1.12) Si rimanda ai testi di elettrodinamica classica per la dimostrazione di tale relazione 10CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA dove e è la carica elettrica e m la massa della particella. Inoltre se la particella oscilla intorno una certa posizione di equilibrio essa emette energia pari a: dεem = 2e2 ω 2 Ēdt 3mc3 (1.13) con ω = frequenza angolare di oscillazione (ω = 2πν) e Ē= energia media degli oscillatori alla temperatura T. L’equazione 1.13 si ottiene dall’equazione di Larmor che stabilisce che la potenza irradiata da una carica elettrica accelerata è: 2 Wem = 3 q 2 |v̇|2 3c dove q è la carica e v̇ la sua accelerazione. Assumendo che le cariche sulla superficie della cavità si muovono di moto armonico, ossia soggetti ad una forza di richiamo del tipo: F = −kx, l’accelerazione a cui è soggetta una particella è: |v̇| = kx/m. Ricordando che la frequenza di oscillazione è data dalla relazione: r 1 k , ν= 2π m si ottiene: |v̇| = ω 2 x. L’espressione precedente contiene la variabile x incognita. È possibile esprimere la x attraverso un’altra grandezza di cui possiamo conoscere il valor medio in funzione della temperatura, ossia l’energia media dell’oscillatore. Considerando che per un oscillatore armonico l’energia totale è data da: 1 1 ω 2 A2 Etot = T + V = kA2 = 2 2 m con A che denota l’ampiezza massima di oscillazione, ne risulta che il termine ω 2 x2 può essere sostituito dal rapporto Ē/m, dove Ē è una sorta di energia 1.3. 11 LO SPETTRO DEL CORPO NERO media dell’oscillatore. Cos’ facendo si ottiene: Wem = 2 2 2 4 2 q ω x = 3 q 2 ω 2 Ē 3 3c 3c Planck partı̀ dall’ipotesi che le particelle che costituiscono le pareti della cavità avessero elettroni debolmente legati (elettroni di valenza) che fossero responsabili dell’assorbimento ed emissione della radiazione. Assorbendo energia questi elettroni oscillano e, in accordo con la meccanica classica, emettono energia sotto forma di radiazione elettromagnetica. All’equilibrio termico, quando cioè la radiazione emessa è stazionaria: εass = εem , (1.14) 2e2 ω 2 πe2 uν dt = Ēν dt 3m 3mc3 (1.15) ovvero: con: ω =2πν. Risolvendo rispetto a uν : uν = 8πν 2 Ēν 2ω 2 Ēν = . c3 π c3 (1.16) Per determinare l’energia media degli oscillatori, Planck utilizzò la distribuzione di Boltzmann, che stabilisce che all’equilibrio termico la frazione di particelle dNE /N che possiede energia E è: dNE = cost e−E/kB T , N dove N è il numero totale di particelle e kB è una costante denominata costante di Boltzmann. L’energia media posseduta da ogni oscillatore ad una certa temperatura è: R∞ Eν dNEν 0 Ēν = R∞ 0 R∞ Eν N0 exp (−Eν /kB T ) dEν 0 dNEν = R∞ , N0 exp (−Eν /kB T ) dEν 0 Ponendo x = Eν /kB T ( dEν = kB T dx), si ottiene (1.17) 12CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA 2 2 N0 kB T Ēν = N0 kB T R∞ x exp (−x) dx 0 R∞ = kB T. (1.18) exp (−x) dx 0 Si osservi che l’energia media non dipende dalla frequenza. La densità di energia uν si ottiene sostituendo la eq. (1.18) nella eq. (1.16): 8πν 2 kB T, (1.19) c3 che è proprio la legge di Rayleigh-Jeans. Catastrofe ultravioletta Secondo le leggi dell’elettrodinamica classica, questo risultato deve valere per qualsiasi frequenza ed a qualsiasi temperatura; invece la eq. (1.19) si accorda con le curve sperimentali solo per quel che riguarda l’andamento a basse frequenze. Ad alte frequenze lo spettro sperimentale presenta un massimo e decade esponenzialmente ed è evidente che tale andamento non è previsto dalla eq. (1.19). L’espressione 1.19 non presenta alcun massimo e non segue la legge di Wien per le alte frequenze. Per ogni valore di T , l’equazione 1.19 rappresenta nel piano ν, uν una parabola con vertice nell’origine. Al crescere della frequenza, la densità di radiazione uν aumenta monotonamente, tendendo ad infinito per ν → ∞. Questo risultato è inaccettabile ed è passato alla storia con il nome di catastrofe ultravioletta. Il fatto che la stessa equazione si accordi con i dati sperimentali solo per frequenze basse suggerisce che nella realtà le alte frequenze fossero“tagliate” da qualche meccanismo non presente nella meccanica classica. Tale meccanismo deve far parte delle leggi fondamentali della natura, dal momento che si è dimostrato che la legge di emissione del corpo nero è universale, indipendente dalla natura del corpo. Questo nuovo principio si trovò grazie al lavoro di Planck, che, modificando il procedimento che lo aveva condotto alla legge di Rayleigh-Jeans, propose la giusta forma di uν . Il modello a stati discreti di Planck Gli integrali che appaiono nella eq. (1.17) corrispondono all’ipotesi classica secondo la quale l’energia è una viariabile continua. Planck dimostrò che abbandonando questa ipotesi era possibile ottenere un’espressione per uν che si accordasse con i dati sperimentali. Ciascuno dei due integrali che compaiono nella eq. (1.17) può essere riscritto come sommatoria su quantità infinitesime di energia: uν = 1.3. 13 LO SPETTRO DEL CORPO NERO Ē = ∞ P nε exp (−nε/kB T ) lim n=0 ∞ P ε→0 (1.20) exp (−nε/kB T ) n=0 Se ora si rende ε finito, ammettendo quindi che solo alcuni valori di energia sono permessi, e si pone x = exp (−ε/kB T ), l’espressione precedente diviene:5 P n nx nεx n Ē = P n = εx P n x x n n d εx dx n−1 P = n P P nn x x n = εx ε εx/ (1 − x)2 = = , 1/ (1 − x) 1−x 1/x − 1 n cioè: Ē = (1.21) ε (1.22) eε/kB T − 1 che è ben diversa dal valore classico Ē = kB T . Sostituendo nella eq. (1.16), si ottiene: uν = ε 8πν 2 c3 exp (ε/kB T ) − 1 (1.23) Affinché la (1.23) soddisfi la legge di Wien basta porre: ε = hν (1.24) È facile controllare che l’espressione di uν è ora corretta sia per basse che per alte frequenze. Infatti per frequenze piccole possiamo sviluppare l’esponenziale in serie di potenze intorno a ν = 0: exp(hν/kB T ) = 1 + hν/kB T, per cui: uν = hν 8πν 2 8πν 2 ≈ kB T, c3 exp (hν/kB T ) − 1 c3 (1.25) in accordo con la legge di Rayleigh-Jeans. Se invece ν è grande exp(hν/kB T >> 1 e quindi: 5 Si ricordi che per x < 1, come nel nostro caso, la serie geometrica P n xn vale 1/(1−x) 14CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA 8πhν 3 exp (−hν/kB T ) (1.26) c3 in accordo con la legge di Wien. Planck postulò che, per un oscillatore di frequenza ν, l’energia permessa potesse variare secondo multipli interi della grandezza hν; h è una costante chiamata costante di Planck il cui valore numerico, dedotto interpolando lo spettro del corpo nero, è 6.626 × 10−34 Js. L’equazione eq. (1.23) conduce anche alla legge di Stefan-Boltzmann ed alla legge di spostamento di Wien ed inoltre permette di esprimerne le costanti di proporzionalità misurate sperimentalmente in termini delle costanti universali h, c e kB . Per quanto riguarda la legge di Stefan-Boltmzmann, basta considerare che secondo la legge di radiazione di Planck la densità di radiazione è proporzionale al cubo della frequenza moltiplicata per una funzione del rapporto ν/T , in altre parole uν = ν 3 f Tν . Pertanto: uν = W = Z ∞ uν dν = 0 Z ∞ 3 ν f 0 ν T dν Posto ora x= ν/T si ha: Z ∞ Z ∞ ν 3 4 W = ν f dν = T x3 f (x)dx = cost T 4 T 0 0 (1.27) (1.28) L’ultima eguaglianza deriva dal fatto che il valore dell’integrale è un numero finito dal momento che x3 f (x) tende a zero per x → ∞. Resta infine da provare che la formula di Planck soddisfa la legge dello spostamento di Wien. Ciò semplicemente corrisponde al cercare i punti di estremo della legge di radiazione del corpo nero di Planck: hν d 8πν 2 d uν = =0 3 dν dν c exp (hν/kB T ) − 1 (1.29) La risoluzione della derivata porta alla relazione: −1 hνmax hνmax hνmax exp −1 exp 3− kB T kB T kB T Ponendo x = hνmax /kB T , si ottiene l’equazione trascendente: (1.30) 1.3. 15 LO SPETTRO DEL CORPO NERO 35 35 ex (1−x/3)(−1) 30 30 25 25 20 20 15 15 10 10 5 5 0 0 0.5 1 1.5 2 2.5 3 0 Figura 1.5: Risoluzione numerica dell’equazione trascendente ex = (1 − x/3)−1 ex = (1 − x/3)−1 , (1.31) che deve essere risolta numericamente o graficamente. In figura è mostrata la soluzione grafica, che mostra l’esistenza di una seconda soluzione oltre quella banale x = 0. Detta c1 tale soluzione, abbiamo: xmax = c1 = hνmax , kB T (1.32) ovvero: c1 kB · T, (1.33) h che effettivamente mostra la dipendenza lineare della frequenza di massimo dalla temperatura. Per ottenere l’espressione della densità di energia in funzione della lunghezza d’onda uλ non è sufficiente sostituire a ν il suo corrispettivo c/λ, ma cone visto nel par 1.2 è necessario uguagliare la densità di energia in un intervallino λ,λ + dλ alla densità di energia in un intervallino ν,ν + dν: νmax = −uλ dλ = uν dν da cui: uλ = uν c/λ2 = 1 8πhc 5 λ exp (hν/kB T ) − 1 (1.34) (1.35) È importante ora capire perché la sostituzione di un integrale con una somma su livelli discreti fornisce la giusta formula della radiazione del corpo 16CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA nero. Come si è detto a proposito della catastrofe ultravioletta, la trattazione classica fallisce nel caso delle alte frequenze: è necessario introdurre un meccanismo che tagli le alte frequenze. Il meccanismo proposto da Planck assume che affinché una frequenza entri in gioco nello spettro del corpo nero è necessario che ci siano due stati, la cui energia differisca di hν, tra i quali possa avvenire scambio di energia per via radiativa. Il processo di assorbimento di energia comporta il passaggio di un oscillatore da uno stato a più bassa energia ad uno a più alta energia, mentre, per quanto riguarda l’emissione è necessario passare da uno stato a più alta energia ad uno a più bassa energia. Per osservare emissione ad una data frequenza ν è perciò necessario che sia popolato uno stato n la cui energia differisca da quello dello stato fondamentale di una quantità: En − E0 = hν La distribuzione di Boltzmann mostra che la probabilità che uno stato sia popolato decade esponenzialmente all’aumentare della sua energia: dNE ∝ exp(−E/kB T ) (1.36) È proprio questo il meccanismo di taglio delle alte frequenze: non si osserva emissione ad alta frequenza nello spettro del corpo nero perché la probabilità di popolare gli stati a più alta energia tende rapidamente a zero all’aumentare dell’energia. Nello stesso modo si spiega perché all’aumentare della temperatura lo spettro si estende nella regione di più alte frequenze e la frequenza di picco aumenta. 1.3.1 Postulati di Bohr La risoluzione di Planck del problema del corpo nero poggia su due assunzioni fondamentali. La prima è che gli oscillatori – gli elettroni di valenza del materiale che costituisce le pareti della cavità, al cui moto sono attribuiti sia l’emissione che l’assorbimento di radiazione – possano assumere solo valori discreti di energia, cosicché nell’applicare la statistica di MaxwellBoltzmann bisogna utilizzare una somma anziché un integrale. La seconda assunzione è che l’energia della radiazione elettromagnetica è direttamente proporzionale alla frequenza, la costante di proporzionalità h fu ricavata per la prima volta da Planck interpolando numericamente i dati sperimentali 1.3. LO SPETTRO DEL CORPO NERO 17 relativi all’emissione delle cavità radianti con l’espressione 1.23. Sulla base di tali assunzioni, una data frequenza ν si osserva nello spettro se e solo se esistono due stati la cui differenza di energia E2 − E1 è proprio uguale a hν e se lo stato ad energia E2 è popolato. Le ipotesi avanzate da Planck si devono accettare come nuovi principi della fisica che riguardano tutti i moti periodici, altrimenti si tratterebbe di ipotesi ad hoc prive di valore scientifico. Esse furono perciò formalizzate da Bohr nei due seguenti postulati: 1. Gli stati stazionari (stabili) di un qualunque sistema fisico non sono in generale tutti quelli previsti dalla fisica classica; vi è un certo numero di stati “permessi” che sono caratterizzati da valori ben determinati ed in generale discreti dell’energia e di altre proprietà. 2. Se un sistema fisico subisce una transizione da uno stato 1 (permesso secondo il postulato precedente) ad un altro stato 2 (anch’esso permesso), e se la transizione avviene con emissione o assorbimento di radiazione elettromagnetica, la frequenza di quest’ultima deve essere pari a: |E2 − E1 | (1.37) ν= h dove E2 ed E1 sono le energie degli stati permessi considerati. Naturalmente, si ha un processo di assorbimento se (E2 − E1 ) > 0 o di emissione nel caso opposto. I postulati di Bohr furono introdotti come principi fondamentali della fisica nella prima fase di sviluppo della meccanica quantistica. Negli sviluppi successivi alla loro enunciazione, in particolare con l’avvento dell’equazione di Schrödinger non ci fu più bisogno di tali postulati, in quanto entrambi sono ricavabili da quest’ultima che, insieme ad altri postulati, fornisce una descrizione dei sistemi microscopici in accordo con le osservazioni sperimentali. I due postulati di Bohr sono validi per qualsiasi sistema fisico, sia esso macroscopico che microscopico, per ragioni che saranno chiare poi, danno risultati incompatibili con la fisica classica solo per sistemi microscopici. 6 6 È bene chiarire che l’espressione “quantizzazione dell’energia” (adoperata spesso) è imprecisa. Una grandezza fisica è quantizzata quando essa può assumere solo valori che sono multipli interi di una certa quantità. La carica elettrica è una grandezza quantizzata in quanto assume solo valori che sono multipli interi della carica dell’elettrone o del protone. Vedremo che il momento angolare di un atomo è quantizzato perché può assumere solo valori che sono multipli interi della costante di Planck. 18CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA Estratto da : N. Bohr , ”On the quantum theory of line spectra” ”La teoria quantistica degli spettri a righe si fonda sui seguenti presupposti fondamentali: -Che un sistema atomico può sempre e soltanto esistere in una certa serie di stati corrispondenti ad una serie discontinua di valori per la sua energia, e che perciò qualsiasi variazione dell’energia del sistema, incluse emissione ed assorbimento di radiazione elettromagnetica, deve avvenire mediante completa transizione tra due stati. Questi stati verranno indicati come ’stati stazionari’ del sistema. - Che la radiazione assorbita od emessa durante la transizione tra due stati stazionari è “monocromatica” ed ha una frequenza ν data dalla relazione: E ′ − E ′′ = hν dove h è la costante di Planck e dove E ′ ed E ′′ sono i valori dell’energia nei due stati in considerazione. Le ipotesi di Planck, formalizzate nei due postulati di Bohr, forniscono un’immediata spiegazione del perché gli spettri atomici hanno una struttura a righe. 1.4 Modello del corpo nero secondo Einstein Einstein diede una semplicissima derivazione della formula di Planck basandosi sui postulati di Bohr ed ipotizzando per la prima volta il fenomeno dell’emissione indotta, che troverà in seguito un’importante applicazione pratica nel laser. Einstein ipotizzò che all’interno della cavità radiante si instaurasse una situazione di equilibrio dinamico, tale che l’energia totale, e conseguentemente anche le popolazioni dei vari livelli discreti di energia, fosse costante nel tempo. Considerò per semplicità solo due stati, uno stato fondamentale ad energia ǫ1 ed uno eccitato ad energia ǫ2 , ed assunse che la popolazione dei due stati fosse regolata dalla statistica ordinaria di Maxwell-Boltzmann: g1 hν g1 − ǫk1 −ǫT2 g1 e−ǫ1 /kB T N1 = = e B = e kB T , −ǫ /k T 2 B N2 g2 e g2 g2 (1.38) dove g1 e g2 sono i fattori di degenerazione degli stati 1 e 2. Sia dz12 il numero di atomi che passa dal livello 1 al livello 2 per assorbimento di 1.4. MODELLO DEL CORPO NERO SECONDO EINSTEIN 19 radiazione; dz12 sarà proporzionale all’intervallo di tempo, alla popolazione dello stato 1 ed alla densità specifica di radiazione: dz12 = N1 B12 uν dt, (1.39) dove B12 è il coefficiente di proporzionalità che rappresenta la probabilità che un atomo passa dallo stato 1 allo stato 2 per assorbimento di radiazione per unità di tempo e di densità di radiazione. Allo stesso modo, il numero di atomi che dal livello 2 decade al livello 1 è dato dall’espressione: dz21 = N2 (B21 uν + A21 ) dt, (1.40) dove A21 è la probabilità che un atomo decada spontaneamente al livello fondamentale, che quindi non dipende dalla densità del campo elettromagnetico, e B21 è invece la probabilità di emissione stimolata, la probabilità che un fotone alla giusta frequenza induca il decadimento di uno stato eccitato, con emisione di un fotone alla stessa frequenza. Einstein introdusse quindi un concetto nuovo: gli oscillatori che si trovano in uno stato eccitato ad energia E2 , possono decadere allo stato fondamentale non solo per decadimento spontaneo, ma anche per effetto di un’interazione con un fotone, la cui frequenza sia proprio pari a (E2 - E1 )/h. Quando all’interno della cavità si raggiunge una situazione di equilibrio le popolazioni dei due stati energetici deve essere stazionaria, non deve cioè dipendere dal tempo: dz12 = dz21 , (1.41) e quindi: N1 B12 uν = N2 (B21 uν + A21 ) , (1.42) da cui si ricava l’espressione della densità di radiazione: uν = N2 A21 A21 = . N1 B12 − N2 B21 N1 /N2 B12 − B21 (1.43) Sostituendo la eq. (1.38) si ottiene: uν = A21 /B21 g1 B12 hν/kB T e g2 B21 −1 . (1.44) Se si riesce a dimostrare che il fattore moltiplicativo dell’esponenziale vale circa 1 e che il numeratore è proporzionale a ν 3 , l’espressione eq. (1.56) 20CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA coincide con la formula di Planck eq. (1.24) Per tale dimostrazione Einstein considerò due casi limiti, l’uno corrispondente a T tendente ad infinito, l’altro al caso di frequenze piccole per il quale vale la legge di Rayleigh-Jeans. È evidente che all’aumentare della temperatura il contributo alla diseccitazione per emissione spontanea diviene trascurabile, in quanto la potenza della radiazione aumenta con la quarta potenza della temperatura. Pertanto per T → ∞ possiamo trascurare il contributo di decadimento spontaneo nella condizione di equilibrio 1.42: N1 B12 uν dt = N2 B21 uν dt. (1.45) Per T tendente ad infinito vale anche: g1 N1 = N2 g2 (1.46) g1 B21 = . g2 B12 (1.47) Combinando le due condizioni: Inoltre per basse frequenze la eq. (1.44) deve coincidere con la formula di Raleygh-Jeans (uν = 8πν 2 kB T /c3 ), perché quando hν diventa molto piccolo, in questo caso rispetto a kB T , il cosiddetto quanto termico, valgono le leggi della fisica classica. Perciò per hν < kB T : uν = e ne risulta: A21 /B21 hν/k BT − e 1 = A21 kB T 8π = 3 ν 2 kB T, B21 hν c 8πν 3 h A21 = B21 c3 (1.48) (1.49) Sostituendo quest’ultima espressione in quella di uν otteniamo la formula di Planck. La semplice trattazione di Einstein dello spettro di emissione del corpo nero è di notevole importanza in quanto introduce per la prima volta il fenomeno dell’emissione stimolata. Inoltre ha anche il merito di fornire un’espressione che permetta di valutare la velocità di emissione spontanea. L’equazione 1.48 ci fornisce infatti il valore della velocità di radiazione spontanea A21 in termini della velocità di emissione stimolata e della frequenza della transizione. Si osservi la dipendenza della velocità di emis- 1.5. L’EFFETTO FOTOELETTRICO 21 sione spontanea dal cubo della frequenza di transizione. Ciò stabilisce che maggiore è la frequenza della transizione maggiore sarà la probabilità di emissione spontanea. Per questo motivo la spettroscopia di emissione è utilizzata nella regione delle alte frequenze, a partire dal visibile. Nelle regioni a più basse frequenze, IR e microonde, la probabilità di emissione spontanea è bassa e si preferisce perciò registrare lo spettro in assorbimento. Il concetto di emissione stimolata, a quel tempo non ancora osservato sperimentalmente, trovò applicazione pratica sessanta anno dopo, con lo sviluppo dei LASER.7 In un laser l’amplificazione del campo di radiazione avviene proprio per emissione stimolata: un fotone interagendo con un centro radiante che si trova già in uno stato eccitato ne provoca la transizione ad uno stato a più bassa energia, con emissione di radiazione alla stessa frequenza del fotone incidente. Poiché i fotoni sono bosoni, il fotone emesso avrà massima probabilità di avere anche stessa fase e stessa direzione di propagazione del fotone incidente. Facendo avvenire numerosi8 eventi di emissione stimolata, si riesce ad ottenere una situazione in cui si hanno solo fotoni uguali, con stessa fase e direzione di propagazione (coerenza temporale e spaziale), cosicché il segnale può essere amplificato per interferenza costruttiva. 1.5 L’effetto fotoelettrico L’effetto fotoelettrico è anch’esso un fenomeno che riguarda l’interazione tra onde elettromagnetiche e materia. Si basa sulla capacità di vari materiali di emettere elettroni se irradiati con radiazione elettromagnetica ad opportuna lunghezza d’onda. Tale caratteristica è particolarmente importante nel caso di materiali metallici a causa dei loro bassi potenziali di ionizzazione. Si consideri il circuito in figura 1.6, costituito da un galvanometro (G), un generatore di forza elettromotrice (A) ed una campana di vetro all’interno della quale sono contenuti due elettrodi metallici collegati al generatore. All’interno della campana è fatto il vuoto per evitare complicazioni dovuti agli urti tra i fotoelettroni emessi e l’aria. Il circuito di fig. 1.6 è ovviamente un circuito aperto, per cui anche imponendo un’alta differenza di potenziale tra gli elettrodi non si osserva circolazione di corrente. Tuttavia, se uno dei due elettrodi è irradiato con radiazione elettromagnetica ad opportuna 7 8 acronimo di Light Amplifier by Stimulated Emission Radiation in senso statistico 22CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA Figura 1.6: Dispositivo sperimentale per lo studio dell’effetto fotoelettrico. lunghezza d’onda (λ), l’elettrodo si ionizza, i foto-elettroni emessi vengono catturati dall’altro elettrodo e si osserva passaggio di corrente. L’esperienza consiste nell’irradiare il campione metallico con una radiazione elettromagnetica di opportuna λ e misurare l’intensità di corrente prodotta, a diverse differenze di potenziale (ddp) tra il catodo e l’anodo. I fotoelettroni emessi dalla lastra metallica sono accelerati verso l’anodo da ddp positive, mentre ddp negative tendono a riportare l’elettrone sul catodo. L’intensità di corrente osservata in funzione della ddp applicata è mostrata in figura 1.7. Si osservi che l’intensità della corrente (i) aumenta all’aumentare della ddp applicata, fino a raggiungere un “plateau”, che corrisponde a potenziali sufficientemente elevati da far sı̀ che tutti i fotoelettroni emessi raggiungano l’anodo. È importante notare, che anche per valori negativi di ddp, si osserva ancora un’intensità di corrente diversa da zero. Ciò significa che gli elettroni sono emessi con una certa velocità, cosicché è necessario applicare un potenziale negativo, un controcampo per evitare che gli elettroni emessi raggiungano l’anodo ed annullare l’intensità di corrente nel circuito. Le caratteristiche più rilevanti del fenomeno si possono riassumere nei seguenti punti: 1.5. L’EFFETTO FOTOELETTRICO 23 Figura 1.7: Intensità di corrente in funzione della ddp applicata. 1. esiste una frequenza di soglia della radiazione incidente (ν0 ) al disotto della quale non si verifica nessuno effetto; 2. esiste un potenziale d’arresto (stopping potential) V0 , indipendente dall’intensità della radiazione incidente, al di sotto del quale nessun elettrone emesso raggiunge il catodo; 3. l’emissione dei fotoelettroni è istantanea se la frequenza della radiazione incidente è maggiore della frequenza di soglia e non avviene per nulla in caso contrario; Sia V0 il valore del potenziale per il quale l’intensità di corrente risulta nulla. Ricordando che l’energia è il prodotto della carica per il potenziale, e · V0 rappresenta l’energia che bisogna fornire al sistema per evitare che un fotoelettrone emesso arrivi al catodo, in altre parole e · V0 rappresenta l’energia cinetica con cui è emesso un fotoelettrone. Per il principio di conservazione dell’energia eV0 deve essere pari alla differenza tra l’energia del raggio incidente e quella necessaria per estrarre un elettrone dalla lamina metallica che funge da catodo, una sorta di potenziale di ionizzazione che per materiali in fase solida è si denota con il termine funzione lavoro Φ. eV0 = energia della radiazione - Φ 24CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA Tutte queste osservazioni sperimentali erano difficilmente razionalizzabili dalle leggi dell’elettrodinamica classica. Secondo l’elettrodinamica classica, il rilascio di elettroni è sı̀ dovuto all’interazione della materia con il campo elettrico della radiazione incidente, ma il meccanismo di interazione è lo stesso di quello ipotizzato da Planck nella sua trattazione del corpo nero: una carica immersa in un campo elettromagnetico di densità uν assorbe energia secondo la eq. (1.12), producendo un’oscillazione dell’elettrone intorno alla propria posizione di equilibrio. Quando l’ampiezza di oscillazione diventa sufficientemente grande si ottiene la fotoemissione dell’elettrone, con conseguente allontanamento della particella dal metallo. Questa interpretazione era in disaccordo con le osservazioni sperimentali visto che faceva dipendere il fenomeno fotoelettrico dalla densità della radiazione e quindi dall’intensità della radiazione utilizzata per produrre l’effetto e non dalla frequenza. Inoltre, secondo il meccanismo di interazione previsto dall’elettrodinamica classica, è sufficiente irradiare il campione per un tempo sufficientemente lungo a che gli elettroni accumulino energia cinetica pari alla funzione lavoro del materiale, fatto che implica che l’energia è trasferita con continuità e non attraverso pacchetti discreti come ipotizzato da Planck. Si sarebbe quindi dovuto osservare un ritardo tra l’inizio dell’irraggiamento e l’emissione di un fotoelettrone, proporzionale all’intensità della luce utilizzata. Tale ritardo però non era osservato, l’istantaneità del processo, ed il fatto che V0 dipendesse solo dalla frequenza erano perciò chiari indizi che l’elettrodinamica classica, come già per la radiazione del corpo nero, non è in grado di spiegare fenomeni inerenti l’interazione luce-materia. Se si riporta in grafico |V0 | in funzione della frequenza della radiazione si ottiene un andamento lineare come quello mostrato in figura 8. 25 1.5. L’EFFETTO FOTOELETTRICO Figura 8. Effetto fotoelettrico. Dipendenza dell’energia cinetica (-eV0 ) dei fotoelettroni emessi dalla frequenza Einstein per primo osservò che il coefficiente di proporzionalità, la pendenza della retta, era proprio uguale alla costante di Planck, che appariva nella equazione del potere emissivo specifico del corpo nero. Einstein postulò dunque la famosa relazione: E = hν (1.50) L’esistenza di una frequenza di soglia è spiegata immediatamente: l’energia non dipende dall’intensità della radiazione ma dalla frequenza. Quando la frequenza è tale che il prodotto hν non è almeno uguale a Φ l’energia necessaria per estrarre un elettrone dal catodo, l’effetto non avviene, non essendoci energia sufficiente per estrarre gli elettroni. La mancanza di ritardo nell’emissione dell’elettrone fu spiegata da Einstein con l’introduzione del concetto di fotone. L’esperimento avviene come se l’energia della radiazione luminosa fosse concentrata in una piccola porzione di spazio, assimilabile ad un pacchetto d’onda o corpuscolo. Il fatto che a parità di frequenza, l’intensità di corrente aumenta all’aumentare dell’intensità della luce incidente è spiegato affermando che l’intensità è proporzionale alla densità di fotoni del fascio radiante, pertanto maggiore l’intensità radiante, maggiore sarà il numero di fotoni incidenti e quindi il numero di fotoelettroni emessi. L’introduzione del concetto di fotone da parte di Einstein segnava il ritorno alla teoria corpuscolare della luce, proposta già senza successo da Newton. Come vedremo nel prossimo capitolo, l’introduzione del concetto di fotone comporterà notevoli implicazioni sull’interpretazioni di alcuni fenomeni, quali la polarizzazione e l’interferenza, che erano state spiegati con estrema facilità dall’ottica ondulatoria. Sarà necessario introdurre concetti rivoluzionari per riconciliare la teoria ondulatoria con quella corpuscolare e proprio questo tentativo porterà alla nascita della meccanica quantistica. 26CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA 1.6 L’esperienza di Franck-Hertz L’esperienza di Franck-Hertz ha giocato un ruolo importante nello sviluppo della meccanica quantistica, dimostrando che i postulati di Bohr non si applicano solo ai casi di interazione della materia con la radiazione elettromagnetica, ma anche a processi in cui il trasferimento di energia riguarda due corpuscoli microscopici. In questo esperimento atomi neutri sono fatti interagire con un fascio di elettroni, dimostrando che anche in questo caso devono valere le stesse leggi introdotte da Planck e Bohr: un atomo può variare la sua energia interna solo di quantità finite, uguali alle differenze di energia tra gli stati permessi, gli stati stazionari postulati da Bohr. Il dispositivo utilizzato per questa esperienza è mostrato in figura 9; si tratta di uno speciale triodo costituito da un catodo che riscaldato emette elettroni, una griglia che funge da acceleratore di elettroni ed una placca. Figura9: Dispositivo utilizzato per l’esperienza di Franck-Hertz In tale triodo il catodo è collegato a terra e la griglia g, situata a distanza l dal catodo, è collegata ad un potenziometro che permette di portarla ad un potenziale Vg variabile. La placca è tenuta ad un potenziale Vp = Vg − dV ; nell’esperimento ∆V è mantenuto costante. In questo dispositivo gli elettroni emessi dal filamento vengono accelerati dal campo fra il catodo e la griglia, che supporremo, per semplicità, uniforme. Perciò gli elettroni 1.6. L’ESPERIENZA DI FRANCK-HERTZ 27 che raggiungono una distanza x dal catodo, acquistano un’energia cinetica pari a eVg x/l (approssimazione del campo uniforme). Se il potenziale alla griglia è maggiore del controcampo imposto tra la griglia e la placca, se cioè Vg > ∆V , e se gli elettroni giunti all’altezza della griglia non hanno perso energia per urto con altre particelle, la loro energia cinetica T = eVg è sufficiente a superare il controcampo, buona parte degli elettroni giungono alla placca ed un misuratore di corrente opportunamente collegato in serie tra la griglia e la placca rivelerà una corrente crescente al crescere di Vg . Ciò è effettivamente quello che si osserva quando nella campana di vetro contenente il triodo è fatto il vuoto. Le cose cambiano radicalmente se invece vengono introdotti nel contenitore vapori di mercurio, estremamente rarefatti. L’andamento dell’intensità di corrente in presenza di vapori di Hg in funzione di Vg è mostrato in figura 10. Al crescere di Vg , per Vg maggiore ∆V , si osserva che per un tratto iniziale la corrente di placca Ip cresce all’aumentare di Vg , come nel caso in cui non sono presenti vapori di mercurio. Tuttavia, quando Vg raggiunge un valore critico, per il mercurio 4,86 V, la curva di Ip in funzione di Vg presenta un’inflessione, seguita da una progressiva diminuzione. Aumentando ulteriormente Vg , la corrente alla placca raggiunge un valore di minimo relativo e poi riprende a salire. Per un potenziale Vg = 9, 72 V, doppio del precedente, si presenta una nuova inflessione, che dà inizio a una seconda diminuzione di Ip , seguita ancora da un tratto ascendente. In definitiva, si osservano dei picchi di corrente che cadono a valori di Vg multipli interi di un certo potenziale che per il mercurio vale 4.8 V. 28CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA Figura 10. Andamento dell’intensità di corrente in funzione di Vg . Questo andamento della corrente non è facilmente spiegabile se non ipotizzando urti anelastici,9 con cessione di energia tra gli elettroni e gli atomi di Hg. È possibile spiegare il fenomeno come segue. La prima inflessione è dovuta ad urti anelastici che avvengono inizialmente in numero minimo perché gli elettroni raggiungono l’energia di 4,86 eV solo nelle immediate vicinanze della griglia. Al crescere di Vg , la regione in cui gli elettroni hanno energia uguale o maggiore di 4,86 eV diviene più grande e gli urti efficaci più probabili; il numero di elettroni che cedono per urto energia agli atomi di mercurio aumenta e la corrente diminuisce perché l’energia residua di tali elettroni è insufficiente a vincere il controcampo per raggiungere la placca. Quando però Vg aumenta ulteriormente, gli elettroni che hanno subito un urto anelastico con atomi di Hg hanno spazio sufficiente per essere accelerati ed arrivare alla griglia con un’energia cinetica superiore a e·∆V . La corrente ricomincia a crescere, fino a quando non accade che gli elettroni che hanno già ceduto energia per collisione con un atomo di Hg sono accelerati ad una velocità tale da consentire un secondo urto con trasferimento di energia. A questi valori di Vg si osserva una nuova diminuzione della corrente. Allo stesso modo si spiegano tutti gli altri picchi a valori di Vg crescenti. 9 Per urto anelastico si intende qui un urto in cui parte dell’energia cinetica è immagazzinata da una delle due particelle sotto forma di energia interna 1.7. L’EFFETTO COMPTON 29 Si deve concludere che gli atomi di mercurio subiscono collisioni accompagnate da trasferimento di energia a gradi di libertà interni solo quando l’energia trasferita è di 4.86 eV. Questa quantità di energia deve essere proprio quella necessaria a promuovere un atomo di mercurio dallo stato fondamentale ad uno a più alta energia. Questa è già una prima indicazione della validità dei postulati di Bohr, tanto più che determinando la lunghezza d’onda corrispondente ad un quanto di energia di 4.86 eV si trova 254 nm, in ottimo accordo con la lunghezza d’onda della riga di risonanza del mercurio atomico, che cade a 253,62 nm. Aggiungiamo che osservazioni apposite permettono di mettere in evidenza che il triodo descritto emette effettivamente la riga ultravioletta in questione, come dev’essere, giacché gli atomi eccitati per urto devono tornare, prima o poi, allo stato fondamentale. 1.7 L’effetto Compton La conferma definitiva dell’ipotesi del fotone di Einstein si ottenne con il lavoro di Compton, che mette in particolare evidenza il comportamento corpuscolare dei fotoni. L’esperimento di Compton ha infatti fornito un’informazione supplementare riguardo alle proprietà dei fotoni, mostrando che essi non solo posseggono una ben determinata quantità di energia, dipendente dalla frequenza della radiazione, ma hanno anche una precisa quantità di moto. L’esperimento mediante il quale Compton ha verificato l’esistenza dei fotoni consiste nel fare incidere un fascio monocromatico di raggi X su di un campione e misurare a diversi angoli di diffusione l’intensità della radiazione diffusa in funzione di λ. Lo schema dell’esperimento è riportato nella figura 11.È costituito da una sorgente di raggi X, un elemento di dispersione in grado di selezionare una data λ, un diffusore, cioè un cristallo atomico, ed una lastra fotografica o un rilevatore. 30CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA Figura 11. Effetto Compton:l’urto tra l’elettrone ed il fotone conserva la quantità di moto Quando i raggi X colpiscono il cristallo, la radiazione viene diffusa e si propaga in tutte le direzioni. L’intensità della luce diffusa è registrata a diversi valori di θ, l’angolo tra la direzione di propagazione della luce incidente e quella del fotone diffuso, si veda fig. 11. Compton osservò che, sebbene il fascio incidente fosse monocromatico, i raggi diffusi hanno picchi di intensità a due diverse λ, come mostrato in figura 12. Un picco cade sempre alla stessa lunghezza d’onda della radiazione incidente, il secondo picco invece sempre a lunghezze d’onda maggiori del precedente. La differenza tra la lunghezza d’onda dei due picchi dipende dall’angolo di osservazione ed aumenta all’aumentare di quest’ultimo, secondo la relazione: ∆λ = λ′ − λ ≃ 0, 024 × (1 − cos θ) (1.51) con λ espressa in Å. L’esperimento fu ripetuto da Compton usando campioni di diversi materiali, ma la relazione tra le lunghezze d’onda dei due picchi osservati risultò sempre la stessa. Egli concluse pertanto che il fenomeno doveva dipendere non dalle caratteristiche specifiche delle varie sostanze utilizzate, ma dai costituenti stessi della materia, ossia gli elettroni. 1.7. L’EFFETTO COMPTON 31 Figura 12. Effetto Compton: intensità della radiazione diffratta in funzione di λ a diversi valori di θ La presenza di un’onda diffusa a lunghezza d’onda λ′ non può essere spiegata dalle leggi della fisica classica. Infatti secondo la fisica classica un’onda monocromatica di una certa lunghezza d’onda λ dovrebbe indurre un’oscillazione negli elettroni del materiale colpito dalla radiazione esattamente alla stessa frequenza dell’onda incidente. Essendo poi gli elettroni particelle cariche, nel momento in cui oscillano emettono anch’essi radiazione elettromagnetica in tutte le direzioni, alla stessa lunghezza d’onda di quella incidente λ. Compton spiegò i risultati sperimentali ipotizzando che il fascio incidente fosse costituito da corpuscoli, i fotoni, e che questi interagissero con gli elettroni come delle vere e proprie particelle, cosicché l’interazione tra fotoni ed elettroni può essere considerata come un urto elastico tra due particelle. Quando il fotone urta un elettrone può trasferire parte della propria energia a quest’ultimo ed essere riemesso con un’energia minore di quella iniziale. Ciò è possibile perché la radiazione scelta (raggi x) ha “dimensione” (lunghezza d’onda) paragonabile con quella dell’elettrone. L’occorrenza di un urto con parziale cessione di energia dal fotone all’elettrone che lo diffonde spiega perché la λ del secondo picco è sempre maggiore di quella incidente: nell’urto il fotone ha ceduto una parte della propria energia all’elettrone e pertanto il fotone diffuso ha minore energia. 32CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA Il picco occorrente sempre alla stessa λ è invece dovuto ad urti elastici con elettroni di guscio interno, più fortemente legati ai nuclei; questi danno luogo ad urto elastico, senza trasferimento di energia, e pertanto non contribuiscono al cosiddetto spostamento Compton, ossia all’effetto legato alla viariazione di λ. Compton applicò a questo processo di diffusione le leggi della fisica classica che regolano i processi di collisione tra corpuscoli, e cioè la legge di conservazione della quantità di moto e dell’energia. Le due condizioni da soddisfare sono la conservazione dell’energia e della quantità di moto. Per quanto riguarda la condizione di conservazione dell’energia, possiamo scrivere hν = hν ′ + (m − m0 )c2 (1.52) dove (m − m0 )c2 è l’espressione relativistica della variazione di energia dell’elettrone. 1 (1.53) hν = hν ′ + m0 c2 q −1 v 2 1− c Ricordando che ν = c λ si ottiene: hc hc = ′ + m0 c2 λ λ 1 p 1 − (v/c)2 −1 ! (1.54) Per quanto riguarda la conservazione della quantità di moto, è noto che se un oggetto assorbe completamente un’energia U da un fascio di radiazione, il raggio radiante trasferisce all’oggetto un impulso pari a U/c. Ipotizziamo quindi che ogni fotone trasferisca all’oggetto un impulso pari a h/λ. La quantità di moto è una grandezza vettoriale per cui tutte le componenti del vettore quantità di moto devono rimanere invariate per effetto della collisione. Possiamo quindi scrivere due equazioni scalari, una per la componente x e l’altra per la componente y: * Lungo x h m0 v h = ′ cos θ + p cos ϕ; (1.55) λ λ 1 − (v/c)2 * Lungo y 0= m0 v h sin θ + p sin ϕ. ′ λ 1 − (v/c)2 (1.56) 33 1.8. SPETTRI ATOMICI. Abbiamo quindi tre equazioni che regolano la variazione di cinque grandezze: λ,λ′ ,θ, v e ϕ . Possiamo utilizzare due equazioni per eliminare le due grandezze relative all’elettrone, v e ϕ ed ottenere un’equazione che mette in relazione le altre tre quantità. Il risultato è: λ′ − λ = h (1 − cosθ), me c (1.57) dove mhe c =0.024 Å, in perfetto accordo con i risultati sprimentali. La trattazione di Compton riesce a dimostrare con successo le osservazioni sperimentali. La trattazione fatta da Compton considera il processo di diffusione di fotoni come conseguenza di urti elastici tra corpuscoli, elettroni e fotoni, ipotesi che implicitamente ammette che la radiazione ha caratteristiche corpuscolari. 1.8 Spettri atomici. Un altro problema di difficile comprensione che si presentò agli inizi del secolo XX era quello di spiegare la struttura fine degli spettri atomici. La presenza di righe era già stata osservata circa un secolo prima nello spettro della radiazione solare, grazie al lavoro di Fraunhofer (1787-1926). Si tratta di righe nere (oggi se ne conoscono varie migliaia), dovute all’assenza nella radiazione solare di segnale a certe lunghezze d’onda, si veda figura 1.8. Grazie ad un potente spettrometro, almeno per quell’epoca, costruito da se stesso Fraunhofer fu in grado di individuare un certo numero di tali righe. La spiegazione di questo fenomeno risiede nell’assorbimento selettivo della radiazione solare da parte di atomi e molecole presenti nella fotosfera, righe più deboli, o nella cronosfera, righe più intense. Queste righe furono poi identificate anche in emissione ed alcune di loro assegnate a precise speie molecolari. Dato che ogni tipo di molecola o ione ha un proprio spettro di emissione e di assorbimento, caratteristico della specie, lo studio delle righe di Fraunhofer ha dato informazioni rilevanti non solo sulla composizione dell’atmosfera solare, ma, attraverso particolari analisi dell’effetto Doppler sulle righe di Fraunhofer, si sono ottenute indicazioni sul moto dello strato assorbente dell’atmosfera solare. Gli spettri a righe sono comuni a tutte le zone della radiazione elettromagnetica. 34CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA Figura 1.8: Righe di Fraunhofer nella radiazione solare Qui ci occuperemo in particolare dello spettro a righe del sistema più semplice, l’atomo di idrogeno. L’elettromagnetismo classico prevede che cariche in moto accelerato irradino energia elettromagnetica. Per l’atomo di idrogeno, si potrebbe quindi cercare di stabilire una relazione tra la frequenza osservata e la frequenza delle oscillazioni dell’elettrone. L’atomo di idrogeno potrebbe comportarsi come una piccola antenna radio: la radiazione elettromagnetica induce oscillazioni dell’elettrone, possibilmente in un’orbita intorno al protone, e viene quindi assorbita. Questo modello però non si concilia con l’osservazione di uno spettro a righe: l’atomo di idrogeno costituisce, sotto certi aspetti, un sistema isolato al quale non viene fornita energia da fonti esterne, e bisogna dunque apettarsi che la frequenza dell’elettrone e quindi anche della radiazione emessa o assorbita varino con continuità, il che non può conciliarsi con la presenza di righe nette. C’è un’ulteriore, evidente difficoltà: se l’elettrone oscilla intorno al nucleo dovrà emettere energia elettromagnetica, a spese della propria energia cinetica. Diminuendo l’energia cinetica diminuisce anche la forza centrifuga che mantiene l’elettrone ad una certa distanza dal nucleo. Ciò comporta una variazione del raggio dell’orbita dell’elettrone, per cui la distanza elettrone-nucleo cambierebbe continuamente portando alla previsione che l’atomo non è stabile. Bohr superò questa difficoltà ipotizzando, come Planck aveva fatto per spiegare la radiazione del corpo nero, l’esistenza di stati stazionari dell’atomo di idrogeno, da cui esso non emette energia. La radiazione è emessa solo quando l’atomo passa da uno stato stazionario con energia Ei ad un altro stato con energia minore Ej . L’energia emessa è, in accordo con Planck: Ei − Ej = hν (1.58) Per conoscere le frequenze previste, Bohr sviluppò un proprio modello, che ebbe grande influenza sugli sviluppi futuri della meccanica quantistica, alla 35 1.8. SPETTRI ATOMICI. cui base c’è l’ipotesi che l’elettrone si muova in un’orbita circolare di raggio r intorno al protone. Dalla seconda legge di Newton: mv 2 e2 = , 4πǫ0 r2 r (1.59) dove il termine a sinistra rappresenta la forza di attrazione coulombiana e quello a destra il prodotto massa-accelerazione. Possiamo facilmente risalire all’energia cinetica dell’elettrone; assumendo un sistema di riferimento centrato sul nucleo che si muove con esso: T = e2 . 8πǫ0 r (1.60) L’ energia totale del sistema è: E =T +V =− e2 . 8πǫ0 r (1.61) Dal momento che il raggio può assumere qualsiasi valore, lo stesso vale anche per l’energia. Pertanto, nell’ottica classica, fissare specifici valori di energia significa fissare dei valori di r ”permessi”; dato r, tutti le proprietà del sistema sono determinate. La velocità dell’elettrone si può ricavare dalla eq. (1.59): s e2 = v. 4πǫ0 mr La frequenza di rotazione ν0 è data da: s v e2 = . ν0 = 2πr 16π 3 ǫ0 mr3 (1.62) (1.63) La quantità di moto è: p = mv = s me2 , 4πǫ0 r ed infine per il momento angolare si ottiene: s me2 r , L=p×r = 4πǫ0 (1.64) (1.65) 36CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA in quanto per l’assunzione che le orbite sono circolari il vettore quantità di moto è sempre ortogonale al vettore posizione. Bohr trovò che la necessaria quantizzazione del raggio dell’orbita si mettesse in evidenza nel modo più semplice attraverso la quantizzazione del momento angolare, avanzando l’ipotesi che L potesse assumere solo valori che sono multipli interi della costante di Planck h̄. Si osservi che questa è una vera e propria quantizzazione, del tutto analoga a quella della carica elettrica, e di nuovo compare la costante di Planck. Dalla quantizzazione del momento angolare si ottiene: r = n2 h 2 ǫ0 . πme2 (1.66) Sostituendo quest’ultima espressione nella eq. (1.61), si ottiene l’espressione che determina l’energia degli stati stazionari E=− 1 me4 , n2 8ǫ20 h2 (1.67) con n numero intero positivo che può assumere tutti i valori a partire da 1. 1.8. SPETTRI ATOMICI. 37 Figura 13. Diagramma dei livelli energetici dell’atomo di idrogeno indicante i numeri quantici dei vari livelli ed alcune delle transizioni che compaiono nello spettro. La formula di Bohr permetteva immediatamente di spiegare il principio di combinazione di Ritz; infatti, poiché ∆E=hν, una transizione tra due stati quantici è prevista cadere a frequenza : 1 1 me4 , (1.68) − ν= 2 2 8ǫ0 h j 2 i2 Ora, indicando con RH , costante di Rydberg, la quantità: 38CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA RH = me4 , 4ǫ20 ch3 (1.69) otteniamo la formula di Ritz per il calcolo delle lunghezze d’onda corrispondenti alle righe atomiche: 1 1 1 , (1.70) = RH − λ j 2 i2 Figura 14. Diagramma dei livelli energetici dell’atomo di idrogeno indicante i numeri quantici dei vari livelli ed alcune delle transizioni che compaiono nello spettro. 1.9 Principio di corrispondenza Le evidenze sperimentali a favore dell’ipotesi degli stati discreti avanzata da Planck iniziarono ad essere numerose e tutte coerenti tra loro. Il valore della costante di Planck ottenuto dallo studio della radiazione del corpo nero si accordava perfettamente con quello ottenuto da Einstein dalla variazione del potenziale di soglia nell’effetto fotoelettrico e con quello ottenuto da Bohr dallo spettro a righe dell’atomo di idrogeno. Nonostante ciò la nuova teoria non si sarebbe mai affermata se Bohr non avesse mostrato come le predizioni ottenute da questa si accordavano perfettamente a quelle 1.9. PRINCIPIO DI CORRISPONDENZA 39 ottenibili dalle leggi della fisica classica, quando le dimensioni dei sistemi tendevano al limite macroscopico. Bohr formulò un principio, noto con il nome di principio di corrispondenza, che stabilisce che per numeri quantici molto grandi, la fisica quantistica si riduce alla fisica classica. Solo cosı̀ si riuscirono a superare le inevitabili resistenze del vecchio mondo scientifico. Il raggio dell’orbita dell’elettrone intorno al nucleo nell’atomo di idrogeno si ottiene ponendo n=1 nella (eq. (1.66)). Per n=1 si ottiene 5.3 10−11 , ma se si pone n=10000 il raggio diventa n2 volte più grande ossia dell’ordine dei millimetri. Questo atomo è cosı̀ grande da far pensare che il suo comportamento possa essere descritto esattamente dalla fisica classica. Verifichiamo che ciò sia vero, calcolando la frequenza emessa sia utilizzando lo schema classico che l’ipotesi quantistica. Classicamente la frequenza emessa è uguale al numero di rivoluzioni che l’elettrone effettua nell’unità di tempo: ν class = v 2πr (1.71) Sostituendo l’espressione di v ottenuta in precedenza, otteniamo il valore della frequenza secondo la fisica classica ν class = me4 1 4ǫ20 h3 n3 (1.72) La frequenza di emissione secondo il modello quantistico, considerando una transizione da n a n+1, è 2n + 1 1 1 quant = RH (1.73) ν = RH 2 − n (n + 1)2 (n + 1)2 n2 Quando n è grande l’espressione in parentesi quadra tende a 2/n3 . Ne segue che: 2 (1.74) ν quant = RH 3 n Sostituendo il valore di RH , c.f. eq. (1.69): ν quant = me4 1 4ǫ20 h3 n3 (1.75) Abbiamo dimostrato che per dimensioni macroscopiche la frequenza classica coincide con quella quantomeccanica. Questo risultato è noto con il nome 40CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA di proncipio di corrispondenza e sancisce che per sistemi macroscopici la meccanica quantisitca coincide con quella classica. 1.10 Onde e Corpuscoli: l’ipotesi di de Broglie Partendo dalla considerazione che la natura è generalmente simmetrica, Louis de Broglie, all’epoca studente di dottorato, estese le proprietà della radiazione elettromagnetica a corpuscoli microscopici. Se la radiazione elettromagnetica in alcuni esperimenti mostra natura ondulatoria ed in altri natura corpuscolare perché la stessa caratteristica non può essere estesa anche ad un fascio di particelle ben collimato? de Broglie avanzò pertanto la rivoluzionaria ipotesi che ad una particella in moto a velocità v dovesse essere associata una lunghezza d’onda: λ= h h = , p mv (1.76) cioè la stessa relazione che lega lunghezza d’onda e quantità di moto nella radiazione elettromagnetica. Utilizzando la relazione precedente, de Broglie riuscı̀ ad ottenere la condizione di quantizzazione della componente z del momento angolare postulata da Bohr. Assumiamo infatti che il moto di rotazione dell’elettrone intorno al nucleo sia associato ad un’onda stazionaria. La condizione di stazionarietà per un’onda in oscillazione tra due fermi è che la distanza tra i fermi deve essere uguale ad un numero intero di mezze lunghezze d’onda. Applichiamo tale condizione ad un’orbita di Bohr, considerando però che in questo caso abbiamo bisogno che l’onda prodotta dalla prima rivoluzione effettuata dall’elettrone intorno al nucleo interferisca in maniera costruttiva con l’onda relativa al nuovo moto di rivoluzione. Dal momento che lo spazio percorso tra due successive oscillazioni di un elettrone intorno al nucleo è 2πr, la condizione di stazionarietà è: 2πr = nλ, n = 1, 2, 3, 4 (1.77) Sostituendo alla lunghezza d’onda l’espressione ipotizzata da de Broglie: 1.10. ONDE E CORPUSCOLI: L’IPOTESI DI DE BROGLIE 41 Figura 1.9: Un’artistica visione dell’atomo di idrogeno mostrante l’elettrone che ruota intorno al nucleo descrivendo un’orbita stazionaria secondo de Broglie, che si ripete identicamente dopo un giro completo h 2πr = n , p pr = n h 2π (1.78) dal momento che le orbite sono circolari pr = Lz e ne consegue la condizione di quantizzazione del momento angolare introdotta da Bohr per spiegare lo spettro dell’atomo di idrogeno. L’ipotesi di de Broglie trovò conferma sperimentale pochi anni dopo, quando Davisson e Germer nel 1927 osservarono per la prima volta fenomeni di diffrazione facendo incidere un fascio di elettroni su di un cristallo di nichel. 42CAPITOLO 1. LE BASI SPERIMENTALI DELLA MECCANICA QUANTISTICA 1.11 L’equazione di Schrödinger Per sviluppare ulteriormente le nuove idee emerse dalle osservazioni effettuate su scala microscopica è necessario trovare l’equazione che fornisse gli stati stazionari postulati da Bohr. Questo problema fu affrontato con successo da Schrödinger, il quale propose la famosa equazione: HΨ = EΨ dove H è il cosiddetto operatore hamiltoniano e Ψ è la funzione d’onda. La risoluzione di questa equazione ad autovalori ed autofunzioni permetteva di trovare le energie degli stati stazionari postulati da Bohr ed associava a tali stati una funzione d’onda sul cui significato fisico torneremo tra breve. L’equazione di Schrödinger è un postulato della meccanica quantistica ed è quindi da considerarsi come un principio primo della fisica, non derivabile. È però interessante discutere il percorso che fu impiegato per il raggiungimento di questa equazione. Il fatto che l’equazione che fornisce gli stati stazionari debba necessariamente essere un’equazione ad autofunzioni risulterà chiaro nel prossimo capitolo, quando studieremo l’effetto di una misura su un sistema microscopico. Qui illustriamo un percorso fisicamente ragionevole che conduce all’equazione di Schrödinger partendo dall’equazione delle onde di D’alembert nella sua forma più generale ed introducendo l’ipotesi di de Broglie.10 Si parta dall’equazione generale di D’Alembert che regola il moto ondulatorio: 1 ∂ 2 Φ(x, y, z, t) ∇2 Φ(x, y, z, t) = 2 v ∂ 2t dove Φ(x, y, z, t) fornisce l’ampiezza delle oscillazioni in funzione delle coordinate e del tempo, v è la velocità dell’onda e ∇2 è il laplaciano ∇2 = ∂2 ∂2 ∂2 + + ∂x2 ∂y 2 ∂z 2 Le soluzioni dell’equazione di D’Alembert possono essere fattorizzate in un prodotto di una funzione delle sole coordinate ed una funzione del tempo. Assumiamo per semplicità che il moto ondulatorio avvenga in una sola direzione: 10 Sembra che questa era la strada utilizzata da Wolfgang Pauli nelle sue lezioni al politecnico di Zurigo 43 1.11. L’EQUAZIONE DI SCHRÖDINGER Φ(x, t) = Ψ(x)cos(ωt + c) Sostituendo nell’equazione alle onde: ω2 4π 2 ∂2 Ψ(x) = − Ψ(x) = − Ψ(x) ∂x2 v2 λ2 Introduciamo ora l’ipotesi di de Broglie λ = (1.79) h p ∂2 4π 2 p2 Ψ(x) = − 2 Ψ(x) ∂x2 h Poiché l’energia del sistema può essere scritta comme somma di energia cinetica ed energia potenziale E =T +V = p2 + V (x) 2m p2 = 2m(E − V (x)) Sostituendo l’equazione alle onde si scrive: ∂2 4π 2 Ψ(x) = − 2m (E − V (x)) Ψ(x) ∂x2 h2 −h̄2 ∂ 2 Ψ(x) + V (x)Ψ(x) = EΨ(x) (1.80) 2m ∂x2 che è la ben nota equazione di Schrödinger , che fornisce gli stati stazionari e le relative energie di una particella in moto lungo la direzione x e sottoposta ad un campo di energia potenziale V (x). La funzione Ψ(x) è detta funzione d’onda della particella. Il modulo quadro di tale funziona rappresenta, secondo l’intepretazione probabilistica della Scuola di Copenaghen, la funzione densità di probabilità di trovare la particella in un certo volumetto infinitesimo dello spazio, si veda paragrafo ?? 3.7 per ulteriori approfondimenti.