Appunti di
Chimica 1
Prof. Guido Busca
Prof. G. Caracciolo
STRUTTURA ATOMICA DELLA MATERIA
Democrito V-IV sec. a . C.
Ripresa, a livello filosofico, nel XVII secolo
Sviluppo scientifico, a cavallo tra il XVIII e il XIX secolo:
- Osservazione di reazioni chimiche semplici.
- Misura dei pesi dei reagenti e dei prodotti
- Misura dei volumi dei reagenti e dei prodotti gassosi
- Individuazione di alcune specie chimiche come "elementi" e di altre come "composti"
( per esempio idrogeno, ossigeno e acqua)
LEGGE DELLA CONSERVAZIONE DELLA MASSA
Lavoisier 1785
Nelle miscele reagenti la massa totale si conserva.
LEGGE DELLE PROPORZIONI DEFINITE
Proust 1799
In ogni composto il rapporto ponderale fra gli elementi che lo costituiscono è definito e costante
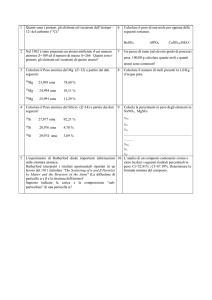
LEGGE DELLE PROPORZIONI MULTIPLE
Dalton 1807
Quando due elementi possono combinarsi insieme in rapporti ponderali diversi per dare composti
diversi, le quantità di uno di essi che nei vari casi si combinano con la medesima quantità dell' altro
stanno fra loro in rapporti espressi da numeri interi generalmente piccoli.
es. ossidi di azoto: rapporto O:N
N2O
NO
N2O3
NO2
N2O5
1:2
2:2
3:2
4:2
5:2
LEGGE DI GAY-LUSSAC
Gay-Lussac, 1808
Quando due gas si combinano fra loro, il rapporto fra i volumi dell' uno e dell' altro che reagiscono
insieme è espresso da numeri interi e piccoli. Lo stesso vale fra i reagenti e i prodotti, se sono
gassosi.
IPOTESI DI AVOGADRO
Avogadro, 1811
In uguali condizioni di temperatura e pressione, uguali volumi di gas diverso contengono lo stesso
numero di particelle (atomi o molecole ?)
DETERMINAZIONE DELLA SCALA DEI PESI MOLECOLARI RELATIVI (almeno per i
gas)
Definizione della Unità di Massa Atomica (u.m.a.)
Inizialmente si prese come peso molecolare di riferimento il peso atomico dell' idrogeno
molecolare, fissato = 2 uma. L' atomo di idrogeno pesava quindi 1 uma.
Poi si decise di definire 1 uma = 1/12 della massa atomica dell'isotopo più stabile dell' atomo di C,
il 12C
USO DELL' IPOTESI DI AVOGADRO PER LA MISURA DEI PESI ATOMICI
Cannizzaro, 1858.
Composto
Ossigeno
Acqua
Acqua ossigenata
Ossido di carbonio
Anidride Carbonica
Ossido d’ Azoto
Anidride solforosa
Anidride solforica
Formula Peso
molecolare
O2
32
H2O
18
H2O2
34
CO
28
CO2
44
NO
30
SO2
64
SO3
80
Peso dell’ ossigeno contenuto nell peso
molecolare (in grammi)
32
16
32
16
32
16
32
48
DEFINIZIONE DI MOLE (GRAMMOMOLECOLA O GRAMMOATOMO)
Una quantità macroscopica di una sostanza chimica che è rappresentata, espressa in grammi, da un
numero uguale al suo peso molecolare o atomico espresso in uma.
IL NUMERO DI AVOGADRO N. Quante molecole ci sono in una mole ?
N è l' inverso dell' unità di massa atomica.
Determinazione di N: inizio XX secolo
N = 6.023 . 1023
1 uma = 1.66 . 10-24 g
La maggior parte degli atomi ha un peso atomico molto vicino ad un multiplo intero del peso
atomico dell' atomo dell' idrogeno:
Protoni =
Neutroni =
Elettroni =
1.67252 . 10-24 g
1.67482 . 10-24 g
9.109 . 10-28 g
Motivi per cui i pesi atomici non sono interi esatti:
- difetto di massa
- abbondanza isotopica
- (peso degli elettroni)
=
=
=
1.00728 uma
1.00867 uma
0.00054 uma = 1/1822 uma
PARTICELLE SUBATOMICHE
Evidenza elettroni e protoni: raggi catodici (Hittorf, 1869).
Scoperta della radioattività (Becquerel, 1896).
Esperienza di Rutherford (1910-1911): la materia è fatta di vuoto ?
Esperienza di Thomson (1912): scoperta degli isotopi.
Nucleo -Protoni ( + )
-Neutroni
Elettroni ( -)
Rappresentazione di un atomo AZX
Z = N. atomico = N. della carica nucleare = N. di protoni = N. di elettroni.
A = N. di massa = N. di protoni + N. di neutroni ~ massa atomica.
ISOTOPIA
isotopi dell' idrogeno
l H = prozio (idrogeno normale)
l
2 H = deuterio = D
1
3 H = trizio = T
1
99.985%
0.015%
artificiale
Z= 1 A= 1 1 protone
Z = 1 A= 2 1 protone, 1 neutrone
Z = 1 A= 3 1 protone, 2 neutroni
massa atomica dell' idrogeno 1.00794 uma
isotopi del carbonio
12C
98.90%
Z = 6 A= 12
13C
1.10%
Z = 6 A= 13
14C (radioattivo)
Z = 6 A= 14
6 protoni + 6 neutroni
6 protoni + 7 neutroni
6 protoni + 8 neutroni
massa atomica del carbonio 12.011 uma
isotopi del cloro : :
35Cl
75.77%
37Cl
24.23 %
Z = 17 A= 35
Z = 17 A= 37
17 protoni + 18 neutroni
17 protoni + 20 neutroni
massa atomica 35.4527 uma
isotopi del bromo
79Br
50.69%
Z = 35 A= 79
81Br
49.31 %
Z = 35 A= 81
35 protoni + 44 neutroni
35 protoni + 46 neutroni
massa atomica79,904 uma (ma l’isotopo 80Br non esiste)
ATOMO DI IDROGENO – MODELLI “CLASSICI”
1. J. J. Thomson (1904)
2. E. Rutherford (1911, premio Nobel nel 1908 per l’ esperienza di R.)
L’ elettrone dovrebbe emettere un radiazione, perdendo energia. Dovrebbe quindi
emettere una radiazione di energia decrescente e dovrebbe cadere sul nucleo in 10 -11
secondi.
3. N. Bohr (1913, premio Nobel nel 1922): ipotesi quantistica.
Deriva dall’ ipotesi di Plank, E = h .
L’ elettrone non emette alcuna radiazione = stati stazionari.
Quantizzazione del momento angolare:
mvr = nh/2
Attrazione del nucleo sull’ elettrone (unità di misura cgs):
f = ma = e2/r2
Accelerazione centripeta:
a = v2/r
Quindi:
e2/r2 = m v2/r
r = n2 h2 / 42me2
Energia cinetica
T = mv2/2 = e2/2r
Energia potenziale
V = -e2/r
Energia totale
E = -e2/r + e2/2r = - e2/2r = - 22me4/ n2h2
FENOMENOLOGIA TIPICA DELLE PARTICELLE MATERIALI
- riflessione
- rifrazione
descritte tramite la Meccanica Classica (Newton)
FENOMENOLOGIA TIPICA DELLE ONDE
-interferenza
-diffrazione
descritte tramite la Meccanica Ondulator;n
PARTICELLE SUBATOMICHE: particelle, ma con carattere ondulatorio
LA LUCE E LE ALTRE RADIAZIONI ELETTROMAGNETICHE
Maxwell (1831-1879)
c = velocità della luce nel vuoto (una costante universale) = 2.977 108 m/s
= lunghezza d'onda [lunghezza]
= frequenza [tempo-l]
E = energia
=c/
E= h = h c/
h= costante di Planck (una costante universale) = 6.626 10-34 J.s
Fotone: quanto (particella di massa nulla) di energia E
Teoria della relatività (Einstein, 1905) = in casi particolari, l' energia si
trasforma in massa
Relazione relativistica E= mc2
= h/mc (relazione tra la lunghezza d'onda e la massa che può produrre
LE ONDE DI DE BROGLIE (1924)
ad ogni particella si associa un’ onda tale che:
= h/mv
.
PRINCIPIO DI INDETERMINAZIONE DI HEISENBERG (1927)
x .p h dove p= m v (p = quantità di moto, m = massa, v = velocità)
quindi x .v= h/m
EQUAZIONE DI SCHRÖDINGER (1926)
(2/x2 ) + (2 / y2 ) + (2 / z2 )+ (82m / h2) (E -V) = 0
dove
SOLUZIONI DELL' EQUAZIONE DI SCHRÖDINGER
(x,y,z) = funzione d'onda, di tipo probabilistico, funzione delle coordinate
spaziali (cartesiane). Esprimibile alternativamente come funzione delle coordinate polari:
(r,,)
E = energia della particella (elettrone) AUTOVALORI
AD OGNI FUNZIONE (x,y,z) CORRISPONDE UN SOLO AUTOVALORE E,
MENTRE AD OGNI AUTOVALORE E POSSONO CORRISPONDERE PIU'
FUNZIONI D'ONDA (x,y,z)
V = energia potenziale, la cui espressione dipende dal sistema studiato.
per l'atomo di idrogeno: V= -e2/r
E = - 22me4 / h2n2
dove:
m = massa della particella (elettrone)
e = carica della particella
h = costante di Planck
= 3.14159
n 1 (intero) numero quantico principale
restrizioni quantiche
|p| = l(l+1)h/2
pz = ml h/2
1 = numero quantico secondario = intero 0 1 n-1
ml = numero quantico magnetico = intero -l ml +l
Ogni stato energetico dell ' elettrone definito da una terna di valori dei tre numeri
quantici corrisponde a due diversi stati di uguale energia, che si distinguono solo
in presenza di un campo magnetico.
Orientazione del momento magnetico intrinseco dell' elettrone:
numero quantico di spin elettronico= ms = + 1/2 o -1/2
Lo stato di un elettrone è definito da una quaterna di numeri qualltici:
n, l, ml, ms
NUMERI QUANTICI
1. Numero quantico principale
n>0
Quantizzazione dell’ energia
2. Numero quantico secondario o azimutale
0ln
Quantizzazione della quantità di moto orbitale.
-l ml +l
3. Numero quantico magnetico
Quantizzazione della proiezione del momento
della qunatità di moto sulla direzione z di un
campo magnetico esterno
ms = ½
4. Numero quantico di spin
Quantizzazione del momento intrinseco di
quantità di moto e del suo momento magnetico
intrinseco
Lo stato di ogni elettrone è definito da una quaterna di numeri quantici
n, l, ml, ms
n
1
ml
orbitale
1
0
0
ls
2
0
0
2s
2
2
2
1
1
1
-1
0
+1
2px
2py
2pz
3
0
0
3s
3
3
3
1
1
1
-1
0
-1
3px
3py
3pz
3
3
3
3
3
2
2
2
2
2
-2
-1
0
+1
+2
3d
4
0
0
4s
4
4
4
1
1
1
-1
0
+1
4px
4py
4pz
4
4
4
4
4
2
2
2
2
2
-2
-1
0
+1
+2
4d
4
4
4
4
4
4
4
3
3
3
3
3
3
3
-3
-2
-1
0
+1
+2
+3
4f
C00RDINATE P0LARI
x = r sen c0s
y = r sen sen
z = r c0s
Le s0luzi0ni dell' equazi0ne di Schrödinger p0ss0n0 essere espresse c0sì
(r,,) = Rn,l (r) . l,m () . m ()
(r,,) = funzi0ne d' 0nda di tip0 pr0babilistic0
dP = 2dV = pr0babilità
dP/dV = 2 = densità di pr0babilità
2dV = 1 (l’ elettr0ne c’è)
4 r2 2 = distribuzi0ne della pr0babilità