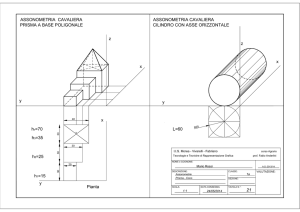
GarchittetturaH RAPPRESENTAZIONE DI OGGETTI CON IL DISEGNO GEOMETRICO Per permettere a chiunque di esaminare un disegno e interpretarlo correttamente, si devono rispettare numerose regole codificate che riguardano: linee; scala di rappresentazione; simbologia; quota e scrittura. Per l’esecuzione dei disegni si utilizzano diversi tipi di carta, la cui scelta dipenderà dal tipo di oggetto da rappresentare (di solito si sceglie tra i formati previsti dalla tabella UNI 936). Prima di eseguire un disegno geometrico si procede alla squadratura del foglio per ottenere un profilo regolare e ricavare dei bordi tra loro perpendicolari. Nel rappresentare un oggetto è necessario adottare un opportuno fattore di scala che consenta di adeguarne le dimensioni al foglio utilizzato, le scale di rappresentazione possono essere sia numeriche che grafiche. La scala numerica o dimensionale viene indicata con numeri che rappresentano il rapporto che intercorre tra le dimensioni dell’ oggetto disegnato (Od) e le dimensioni dell’oggetto reale (Or): 𝑠𝑐𝑎𝑙𝑎 = 𝑂𝑑 𝑂𝑟 Le linee utilizzate nel disegno tecnico si dividono in linee grosse o fini. La scrittura è parte integrante del disegno e si utilizza per titolare il disegno, riportare le dimensioni e le annotazioni, la scala, la data, i materiali ecc. Per fare in modo che l’oggetto venga costruito conformemente all’idea del progettista, il disegno deve essere completato con le indicazioni dimensionali (quote). La quotatura viene eseguita con linee continue e sottili. Quota: è il valore numerico che definisce le dimensioni di un oggetto; per esempio: i disegni dei mobili vengono quotati in centimetri; i disegni meccanici vengono quotati in millimetri; il disegno edile viene quotato in metri; le carte stradali riportano le distanze in chilometri. Linee di misura: indicano le dimensioni dell’oggetto, definite dalle quote. Linee di riferimento: collegano un punto (spigolo) dell’oggetto con gli estremi delle linee di misura oltrepassandole leggermente. COSTRUZIONI GEOMETRICHE ELEMENTARI In questo paragrafo vengono proposti alcuni esercizi e sono descritti procedimenti per realizzare costruzioni geometriche elementari: Dato un segmento AB, costruire la perpendicolare per il suo estremo. Tracciare la bisettrice di un angolo dato AOB. Costruire un triangolo equilatero, dato il lato l. Dato il segmento AB, dividerlo in quattro parti uguali. Dividere un angolo retto in tre parti uguali. Inscrivere un pentagono regolare in una circonferenza. Costruire un quadrato, dato il lato l. Costruire un esagono regolare, dato il lato l PROIEZIONI ORTOGONALI Costruire un ottagono regolare dato il lato l. Per disegnare si possono usare vari metodi che utilizzano la tecnica della proiezione. Le tecniche fondamentali di rappresentazione della geometria descrittiva sono: proiezione centrale o conica; proiezione parallela o cilindrica. Se il centro di proiezione è un punto proprio o reale (Cp) si ha la proiezione centrale o conica dalla quale derivano i sistemi di prospettiva lineari; se invece il centro di proiezione è improprio cioè all’infinito (C∞) si ottiene la proiezione parallela o cilindrica dalla quale derivano le proiezioni ortogonali e assonometriche. La particolare denominazione deriva dal tipo di figura che viene generata da raggi che proiettano una circonferenza su un piano: un cono nel primo caso è un cilindro nel secondo. Il metodo delle proiezioni ortogonali permette di rappresentare un oggetto reale proiettandolo su Proiezione centrale o conica un piano ortogonale a essi; la rappresentazione completa di un oggetto richiede diverse immagini o viste le principali sono: la proiezione orizzontale o pianta; la proiezione verticale o prospetto; proiezione laterale o prospetto laterale. PROIEZIONI ASSONOMETRICHE Proiezione parallela o cilindrica L’assonometria è stata usata fin dall’antichità, per suggerire l’esistenza di una realtà tridimensionale riportata su superfici bidimensionali. Il sistema di rappresentazione assonometrico è un metodo grafico che, a differenza delle proiezioni ortogonali, consente di realizzare una visione tridimensionale dell’oggetto reale che si vuole disegnare, mediante un’unica figura piana. L’assonometria è una proiezione parallela su un piano di proiezione detto anche quadro che coincide con il foglio da disegno. La rappresentazione assonometrica riproduce all’oggetto in maniera approssimata con deformazioni lineari e angolari, la forma è rappresentata tuttavia, benché alterata risulta nel suo complesso molto simile a quella percepita dall’occhio umano. La normativa uni divide le assonometrie in due gruppi: assonometria ortogonale: ottenuta con raggi proiettanti perpendicolari al quadro, che inclinato rispetto agli assi cartesiani di riferimento; assonometria obliqua ottenuta con raggi proiettanti inclinati rispetto al quadro che è assonometria obliqua disposto parallelamente a uno dei piani coordinati per esempio al P.O. I diversi tipi di assonometria si differenziano per la diversa ampiezza degli angoli formati dalle proiezioni degli assi x, y, z, a loro volta le assonometrie ortogonali si dividono nelle seguenti: assonometria ortogonale isometrica: Si ha quando i tre assi formano tra loro angoli uguali di 120° e le tre dimensioni mantengono lo stesso rapporto di deformazione sui tre assi assonometrici; assonometria ortogonale dimetrica: Si ha quando gli assi formano due angoli di 131° e uno di 98° con le misure ridotte alla metà lungo la direzione dell’asse x; assonometria ortogonale trimetrica: si ha quando gli assonometria ortogonale assi formano tra di loro tre angoli diversi e di conseguenza le dimensioni reali dell’ oggetto subiscono riduzioni altrettanto diverse. L’assonometria obliqua o cavaliera si divide in: assonometria obliqua isometrica: si caratterizza per avere gli angoli di 150°, 120°, 90° mentre il porto metrico rimane costante sui tre assi; questo tipo di assonometria prende nome anche di assonometria militare; assonometria obliqua dimetrica o cavaliera: gli assi formano angoli di 135°, 135°, 90°, il rapporto metrico è costante per gli assi z e x ed è ridotto alla metà per l’asse y; assonometria obliqua monometrica: si caratterizza per avere gli assi formanti angoli di 135°, 135°, 90°, con il piano assonometrico disposto parallelamente al P.O., si ottiene così una rappresentazione vista dall’alto, le dimensioni riportate sugli assi x e y non subiscono riduzioni mentre quelle riportate sull’asse z vengono dimezzate o ridotte a 2/3 per simulare l’effetto della vista dall’alto.