caricato da
common.user6305
Gradiente discendente: appunti sull'ottimizzazione

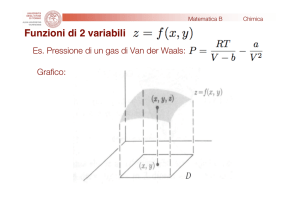
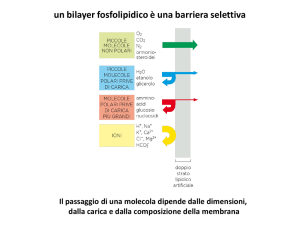
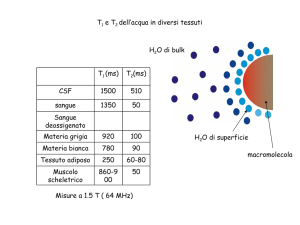
Gradiente discendente Sia θ = [w, b] il vettore di parametri della nostra funzione che vogliamo minimizzare, diciamo inizializzato casualmente e ∆θ = [∆w, ∆b] la variazione nei valori di w, b Ci muoviamo nella direzione di ∆θ, per essere un po' conservativi, ci spostiamo solo di una frazione 𝜂 Per cui il nuovo valore di θ 𝜃𝑛𝑒𝑤 = 𝜃 + 𝜂∆θ Ora ci chiediamo quale è il giusto valore di ∆θ da usare? La risposta viene dallo sviluppo in serie di Taylor della funzione costo. Per semplicità di notazione poniamo u= ∆θ, per cui posto ℒ(θ) la funzione costo abbiamo: 𝜂2 𝑇 2 η3 ℒ(θ + ηu) = ℒ(θ) + η𝑢 ∇θ ℒ(θ) + 𝑢 ∇θ ℒ(θ) + + ⋯ 2! 3! 𝑇 Dato che i valori di 𝜂 2 , η3 , etc, per η che tende a zero, sono trascurabili, la precedente la possiamo riscrivere come: ℒ(θ + ηu) = ℒ(θ) + η𝑢𝑇 ∇θ ℒ(θ) Adesso perché lo spostamento sia favorevole deve risultare che la funzione perdita diminuisca dal passo t a quello t+1, ovvero ℒ(θ + ηu) − ℒ(θ) < 0 Questo implica che deve essere 𝑢𝑇 ∇θ ℒ(θ) < 0 Ora quale è il range di 𝑢𝑇 ∇θ ℒ(θ)? Sia β l'angolo tra u e ∇θ ℒ(θ) poichè sappiamo che, −1 < cos(𝛽) = 𝑢𝑇 ∇θ ℒ(θ) ≤1 ‖𝑢‖ ∗ ‖∇θ ℒ(θ)‖ Moltiplichiamo tutto per ‖𝑢‖ ∗ ‖𝑢𝑇 ∇θ ℒ(θ)‖ −𝑘 < 𝑘 ∗ cos(𝛽) = 𝑢𝑇 ∇θ ℒ(θ) ≤ 𝑘 Poiché, ℒ(θ + ηu) − ℒ(θ) = η𝑢𝑇 ∇θ ℒ(θ) = 𝑘 ∗ cos(𝛽) , sarà più negativo quando cos(𝛽) = −1 ovvero quando 𝛽 = 180 𝑔𝑟𝑎𝑑𝑖. La direzione di u in cui intendiamo muoverci dovrebbe essere a 180°, per cui ci muoviamo in direzione opposta al gradiente. Per cui le equazioni di aggiornamento dei parametri sono: 𝑤𝑡+1 = 𝑤𝑡 − 𝜂∇𝑤𝑡 𝑏𝑡+1 = 𝑏𝑡 − 𝜂∇𝑏𝑡 Dove ∇𝑤𝑡 = 𝜕ℒ(w, b) 𝜕𝑤 ∇𝑏 = 𝜕ℒ(w, b) 𝜕𝑏 Considerazioni Dalla curva in figura, possiamo vedere che: Quando la curva è ripida, il gradiente (∆y1/∆x1) è grande Quando la curva è dolce il gradiente (∆y2∆x2/) è piccolo. Ricordiamo che i nostri aggiornamenti dei pesi sono proporzionali al gradiente w = w − η∇w. Quindi nelle aree in cui la curva è dolce gli aggiornamenti sono piccoli mentre nelle aree in cui la curva è ripida gli aggiornamenti sono grandi. Indipendentemente da dove partiamo una volta che raggiungiamo una superficie che ha una pendenza dolce, il progresso rallenta. Ora supponiamo di prendere fette orizzontali di questa superficie di errore a intervalli regolari lungo l'asse verticale. Come apparirebbe dalla vista dall'alto? Una piccola distanza tra i contorni indica una pendenza ripida lungo quella direzione. Una grande distanza tra i contorni indica una lieve pendenza lungo quella direzione Momentum update Il Momentum update è un altro approccio che ha quasi sempre un miglior tasso di convergenza nelle reti profonde. Questo aggiornamento può essere motivato da una motivazione di carattere fisico del problema di ottimizzazione. Intuizione Se mi viene chiesto ripetutamente di muovermi nella stessa direzione, probabilmente dovrei acquisire un po’di fiducia e iniziare a fare passi più grandi in quella direzione proprio come una palla guadagna slancio mentre rotola giù per un pendio. 𝑢𝑝𝑑𝑎𝑡𝑒𝑡 = 𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒𝑡−1 + 𝜂∇𝑤𝑡 𝑤𝑡+1 = 𝑤𝑡 − 𝑢𝑝𝑑𝑎𝑡𝑒𝑡 Oltre all'attuale aggiornamento, guardiamo anche la cronologia degli aggiornamenti 𝑢𝑝𝑑𝑎𝑡𝑒0 = 0 𝑢𝑝𝑑𝑎𝑡𝑒1 = 𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒0 + 𝜂∇𝑤1 = 𝜂∇𝑤1 𝑢𝑝𝑑𝑎𝑡𝑒2 = 𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒1 + 𝜂∇𝑤2 = 𝛾𝜂∇𝑤1 + 𝜂∇𝑤2 𝑢𝑝𝑑𝑎𝑡𝑒3 = 𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒2 + 𝜂∇𝑤3 = 𝛾(𝛾𝜂∇𝑤1 + 𝜂∇𝑤2 ) + 𝜂∇𝑤3 = 𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒2 + 𝜂∇𝑤3 = 𝛾 2 𝜂∇𝑤1 + 𝛾 𝜂∇𝑤2 + 𝜂∇𝑤3 𝑢𝑝𝑑𝑎𝑡𝑒4 = 𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒3 + 𝜂∇𝑤4 = 𝛾 3 𝜂∇𝑤1 + 𝛾 2 𝜂∇𝑤2 + 𝛾𝜂∇𝑤3 + 𝜂∇𝑤4 𝑢𝑝𝑑𝑎𝑡𝑒𝑡 = 𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒𝑡−1 + 𝜂∇𝑤𝑡 = 𝛾 𝑡−1 𝜂∇𝑤1+𝛾 𝑡−2 𝜂∇𝑤2 … … … 𝜂∇𝑤𝑡 Alcune osservazioni e domande. Anche nelle regioni con pendenze dolci, la discesa del gradiente basata sulla quantità di moto è in grado di fare grandi passi perché la quantità di moto la trasporta. È sempre buono muoversi velocemente? Ci sarebbe una situazione in cui lo slancio ci farebbe andare oltre il nostro obiettivo? Cambiamo i nostri dati di input in modo da ottenere una superficie di errore diversa e poi vediamo cosa succede, in questo caso, l'errore è alto su entrambi i lati della valle dei minimi, lo slancio potrebbe essere dannoso in questi casi. La discesa della pendenza basata sulla quantità di moto oscilla dentro e fuori dalla valle del minimo mentre la quantità di moto la trasporta fuori dalla valle. Fa molte inversioni a U prima di convergere finalmente Nonostante queste inversioni a U converge ancora più velocemente della discesa del gradiente vaniglia. Dopo 100 iterazioni il metodo basato sulla quantità di moto ha raggiunto un errore di 0,00001 mentre la discesa del gradiente vaniglia è ancora bloccato con un errore di 0,36. Qui vediamo l'introduzione di una variabile update che è inizializzata a zero e un iperparametro (𝛾) addizionale. Questa variabile è, in ottimizzazione, nell’analogia fatta con una sfera che rotola da una collina, denominata quantità di moto (il suo valore tipico è circa 0,9), ma il suo significato fisico è più coerente con il coefficiente di attrito. In effetti, questa variabile smorza la velocità e riduce l'energia cinetica del sistema, altrimenti la particella non si arresterebbe mai in fondo a una collina. In fase di cross-validazione questo parametro viene solitamente impostato su valori come [0.5, 0.9, 0.95, 0.99]. In fase di ottimizzazione a volte può giovare un po’di più una schedulazione del Momentum, dove il momento è aumentato nelle fasi successive dell'apprendimento. Un'impostazione tipica è quella di iniziare con un momento di circa 0,5 e portarlo a 0,99 circa su più epoche. Con l'aggiornamento Momentum, il vettore dei parametri aumenterà la velocità in qualsiasi direzione con gradiente costante. Nesterov Momentum Nesterov Momentum è una versione leggermente diversa dell'aggiornamento del momento. Gode di maggiori garanzie teoriche di convergenza per le funzioni convesse e in pratica funziona anche in modo leggermente migliore rispetto al momento standard. L'idea alla base del momento di Nesterov è che quando il vettore del parametro corrente è in una certa posizione x, osservando l'aggiornamento del momento sopra, sappiamo che il termine di aggiornamento da solo (cioè ignorando il secondo termine con il gradiente) sta per spostare il parametro di 𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒𝑡−1 . Pertanto, se stiamo per calcolare il gradiente, possiamo trattare la posizione approssimativa futura w - 𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒𝑡−1 come "lookahead, una sorta di guardare in avanti" - questo è un punto nelle vicinanze di dove stiamo andando a finire. Quindi, ha senso calcolare il gradiente in w+𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒𝑡−1 . invece che sulla posizione vecchia w. Per cui ricapitolando Guardiamo prima di fare il salto Ricordiamo che l’aggiornamento è 𝑢𝑝𝑑𝑎𝑡𝑒𝑡 = 𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒𝑡−1 + 𝜂∇𝑤𝑡 Quindi sappiamo che ci muoveremo almeno di 𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒𝑡−1 e poi di un altro po’ 𝜂∇𝑤𝑡 . Allora perché non calcolare il gradiente() in questo aggiornamento parziale di w invece di calcolarlo usando il valore corrente di 𝑤𝑡 Per cui abbiamo che: 𝑤𝑙𝑜𝑜𝑘_𝑎ℎ𝑒𝑎𝑑 = 𝑤𝑡 − 𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒𝑡−1 𝑢𝑝𝑑𝑎𝑡𝑒𝑡 = 𝛾 ∗ 𝑢𝑝𝑑𝑎𝑡𝑒𝑡−1 + 𝜂𝑤𝑙𝑜𝑜𝑘_𝑎ℎ𝑒𝑎𝑑 𝑤𝑡+1 = 𝑤𝑡 − 𝑢𝑝𝑑𝑎𝑡𝑒𝑡 Il guardare avanti aiuta NAG a correggere la sua rotta più velocemente della discesa del gradiente basata sul momento, quindi le oscillazioni sono minori e le possibilità di sfuggire ai minimi valle sono anche minori Annealing del tasso di apprendimento Nell'addestrare reti profonde, di solito è utile variare il tasso di apprendimento nel tempo. L’intuizione è che con un alto tasso di apprendimento, il sistema contiene troppa energia cinetica e il vettore di parametri rimbalza caoticamente, incapace di stabilirsi nelle parti più profonde e più strette della funzione costo (minimi). Sapere quando far decadere il tasso di apprendimento può essere complicato: farlo decadere troppo lentamente sprecheremo calcoli avendo piccoli miglioramenti per molto tempo. Ma riducendolo troppo aggressivamente, il sistema si fermerà troppo rapidamente, incapace di raggiungere la posizione migliore possibile. Esistono tre tipi comuni di implementazione del riduzione del tasso di apprendimento: Step decay. La riduzione graduale, cioè ridurre il tasso di apprendimento di qualche fattore ogni poche epoche. I valori tipici potrebbero ridurre il tasso di apprendimento di metà ogni 5 epoche o di 0,1 ogni 20 epoche. Questi numeri dipendono fortemente dal tipo di problema e dal modello. Un’euristica che si può vedere nella pratica è osservare l'errore di convalida durante l'allenamento con una frequenza di apprendimento fissa e ridurre il tasso di apprendimento di una costante (ad esempio 0,5) ogni volta che l'errore di validazione cessa di migliorare, ovvero di ridursi. Decadimento esponenziale: ha la forma matematica 𝛼= α𝑜 𝑒 −𝑘𝑡 , dove α0 e k sono iperparametri e t è il numero di iterazione α 0 1 / t decay ha la forma matematica α = 1+𝑘𝑡 dove α0 e k sono iperparametri e t è il numero di iterazione. In pratica, troviamo che il decadimento graduale è leggermente preferibile perché gli iperparametri che esso comporta (la frazione di decadimento e i tempi dei passaggi in unità di epoche) sono più interpretabili rispetto all'iperparametro k. Infine, se puoi permetterti il budget computazionale, sbagli sul lato del decadimento più lento e allenati per un tempo più lungo. Line search In pratica, spesso viene eseguita una ricerca per riga per trovare un valore relativamente migliore di η Aggiornare w utilizzando diversi valori di η, mantenendo quel valore aggiornato di w che fornisce la perdita più bassa. Essenzialmente ad ogni passaggio cerchiamo di utilizzare il miglior valore di scelte disponibili. Qual è il rovescio della medaglia? Stiamo eseguendo molti più calcoli in ogni passaggio. Torneremo su questo quando parleremo di metodi di ottimizzazione del secondo ordine. Vediamo la ricerca di linee in azione. La convergenza è più veloce del gradiente vaniglia discendente Vediamo alcune oscillazioni, ma nota che queste oscillazioni sono diverse da ciò che abbiamo visto in Momentum e NAG. Metodi di apprendimento adattivo per parametro Tutti gli approcci precedenti che abbiamo discusso finora trattano il tasso di apprendimento a livello globale e allo stesso modo per tutti i parametri. La sintonizzazione dei tassi di apprendimento è un processo costoso Adagrad è un metodo di apprendimento adattivo originariamente proposto da Duchi. Il gradiente adattivo lavora sulla singola componente del tasso di apprendimento dividendo il tasso di apprendimento per la radice quadrata di S, che è la somma cumulativa dei gradienti al quadrato attuali e passati (cioè fino al passo t). Si noti che la componente del gradiente rimane invariato come in SGD. Dove S è inizializzato a zero, ε viene aggiunto per evitare la divisione per zero. Si noti che la cache delle variabili ha dimensioni pari alla dimensione del gradiente e tiene traccia della somma per parametro dei gradienti quadrati. Viene quindi utilizzato per normalizzare la fase di aggiornamento dei parametri, in base agli elementi. Si noti che i pesi che ricevono gradienti elevati avranno una riduzione del loro tasso di apprendimento, mentre i pesi che ricevono aggiornamenti piccoli o rari avranno un aumento del loro tasso di apprendimento. L'operazione di radice quadrata risulta essere molto importante e senza di essa l'algoritmo si comporta molto peggio. Il termine eps (solitamente impostato nell'intervallo compreso tra 1e-4 e 1e-8) evita la divisione per zero. Uno svantaggio di Adagrad è che in caso di deep learning, il tasso di apprendimento monotono di solito si rivela troppo aggressivo e interrompe l'apprendimento troppo presto. RMSprop. RMSprop è un metodo di apprendimento adattativo molto efficace, proposto da Geoff Hinton. Nel nostro esempio di prima, se si implementa la discesa del gradiente, possiamo finire con avere enormi oscillazioni nella direzione verticale, mentre si sta cercando di fare progressi in direzione orizzontale. Supponiamo che l'asse verticale è il parametro b e l’asse orizzontale è il parametro w. Potrebbe essere w1 e w2 dove alcuni dei parametri centrali sono stati denominati come b and w per capire meglio. E così, lo scopo è rallentare l'apprendimento nella direzione b, o nella direzione verticale, e accelerare l'apprendimento, o almeno non rallentarlo nella direzione orizzontale. Questo è ciò che RMSprop fa. Ad ogni iterazione t, calcolerà come al solito la derivata dW, db sul mini batch corrente. Ricordiamo che nella direzione orizzontale o in questo esempio, nella direzione w vogliamo imparare ad andare piuttosto veloce. Mentre nella direzione verticale o in questo esempio nella direzione b, vogliamo rallentare tutte le oscillazioni. L'aggiornamento di RMSProp regola il metodo Adagrad in un modo molto semplice nel tentativo di ridurre il suo tasso di apprendimento aggressivo e monotonicamente decrescente. In particolare, utilizza una media mobile di gradienti quadrati, che fornisce: Sdw= β * Sdw+ (1- β) dw2 Sdb= β * Sdb+ (1- β) db2 𝑤=𝑤− 𝛼 𝑏=𝑏− 𝛼 𝑑𝑤 √𝑆𝑑𝑤 + Ɛ 𝑑𝑏 √𝑆𝑑𝑏 + Ɛ Dove β è il tasso di decadimento. In generale possiamo scrivere che α = 0.001 β = 0.9 (raccomandato dagli autori) ε = 10⁻⁶ Qui, il tasso di decadimento β è un iperparametro, valori tipici sono [0.9, 0.99, 0.999]. Si noti che w + = update è identico a Adagrad, ma la variabile cache è "leaky". Quindi, RMSProp modula il tasso di apprendimento di ciascun peso in base alle grandezze dei suoi gradienti, che ha un effetto di equalizzazione benefico, ma a differenza di Adagrad gli aggiornamenti non diventano monotonicamente più piccoli. Quindi con questi termini Sdw e Sdb quello che speriamo è che Sdw sia relativamente piccolo, quindi qui stiamo dividendo per numero relativamente piccolo. Mentre Sdb sarà relativamente grande, così stiamo dividendo per un numero relativamente grande per rallentare gli aggiornamenti sulla dimensione verticale e in effetti se si guardano le derivate, possiamo vedere che le derivate sono molto più grandi nella direzione verticale rispetto alla direzione orizzontale. Quindi la pendenza è molto grande nella direzione b, quindi avremo un db molto grande e un dw relativamente piccolo, quindi db al quadrato sarà relativamente grande, dW al quadrato sarà più piccolo, e quindi Sdw sarà più piccolo. Quindi possiamo usare anche tasso di apprendimento più grande e ottenere un apprendimento più veloce senza divergere nella direzione verticale. Adam. Adam (adaptative momentum) è un aggiornamento recentemente proposto è un RMSProp con Momentum. L'aggiornamento (semplificato) ha il seguente aspetto: 𝑤𝑡+1 = 𝑤𝑡 − 𝛼 √𝑆̂𝑡 + 𝜀 𝑉̂𝑡 Dove Sono le correzioni del bias e Con S e V inizializzati a zero. Nell’equazione di aggiornamento, w viene aggiornato non in base al gradiente attuale, ma in base al gradiente cumulato, è la stessa cosa fatta col metodo del gradiente discendente con momentum. Da dove derivano le correzioni usate? Nota che stiamo prendendo una media corrente delle pendenze come Vt. Il motivo per cui lo stiamo facendo è che non vogliamo fare troppo affidamento sul gradiente corrente e invece fare affidamento sul comportamento complessivo dei gradienti in molti passaggi temporali. Un modo per vedere questo è che siamo interessati al valore atteso dei gradienti e non a un singolo punto stimato calcolato al tempo t. Tuttavia, invece di calcolare E[∇wt] stiamo calcolando Vt come media mobile esponenziale. Idealmente vorremmo che E [Vt] fosse uguale a E[∇wt]. Valori proposti dagli autori: α = 0.001 β₁ = 0.9 β₂ = 0.999 ε = 10⁻⁸ Adam è attualmente raccomandato come algoritmo predefinito da utilizzare e spesso funziona leggermente meglio di RMSProp. Tuttavia, spesso vale la pena provare SGD + Nesterov Momentum come alternativa. L'aggiornamento completo di Adam include anche un meccanismo di correzione del bias, che compensa il fatto che nei primi passi di tempo i vettori m, v sono entrambi inizializzati e quindi polarizzati a zero, prima che si "scaldino" completamente AdaMax AdaMax (Kingma & Ba, 2015) è un adattamento dell’algoritmo Adam degli stessi autori utilizzando le norme di infinito (quindi 'max'). Vè la media mobile esponenziale dei gradienti, e S è la media mobile esponenziale della precedente p-norma dei gradienti, approssimata alla funzione massima come visto di seguito. Dove con V e S iniizializzati a 0. Valori proposti dagli autori: α = 0.002 β₁ = 0.9 β₂ = 0.999 Vi sono anche altri algoritmi proposti Nadam, AMSGrad Intuizione Qui mi piacerebbe condividere con voi qualche intuizione perché gli ottimizzatori di discesa a gradiente utilizzano la media mobile esponenziale per la componente del gradiente e la media mobile del quadrato della radice per la componente del tasso di apprendimento. Perché prendere la media mobile esponenziale dei gradienti? Abbiamo bisogno di aggiornare il peso, e per farlo abbiamo bisogno di fare uso di un certo valore. L'unico valore che abbiamo è il gradiente corrente, quindi utilizziamolo per aggiornare il peso. Ma prendere solo il valore del gradiente corrente non è sufficiente. Vogliamo che i nostri aggiornamenti siano "guidati meglio". Quindi includiamo anche i gradienti precedenti. Un modo per "combinare" il valore del gradiente corrente e le informazioni dei gradienti passati è che potremmo prendere una media semplice di tutte le sfumature passate e correnti. Ma questo significa che ognuno di questi gradienti è pesato allo stesso modo. Ciò non sarebbe intuitivo perché spazialmente, se ci stiamo avvicinando al minimo, i valori di gradiente più recenti potrebbero fornire più informazioni di quelli precedenti. Quindi la scommessa più sicura è che possiamo prendere la media mobile esponenziale, dove i valori di gradiente recenti hanno un peso maggiore (importanza) rispetto ai precedenti. Perché dividere il tasso di apprendimento in base al quadrato medio dei gradienti? L'obiettivo è di adattare la componente del tasso di apprendimento. Adattarsi a cosa? Tutto quello che dobbiamo bisogno di assicurare è che quando il gradiente è grande, vogliamo che l'aggiornamento sia piccolo (altrimenti, un valore enorme verrà sottratto dal peso attuale!). Per creare questo effetto, dividiamo il tasso di apprendimento α per il gradiente corrente per ottenere un tasso di apprendimento adattato. Tenere presente che la componente del tasso di apprendimento deve essere sempre positiva (poiché la componente del tasso di apprendimento, quando moltiplicata con la componente del gradiente, dovrebbe avere lo stesso segno di quest'ultima). Per garantire che sia sempre positivo, possiamo prendere il suo valore assoluto o il suo quadrato. Prendiamo il quadrato del gradiente corrente e "cancelliamo" questo quadrato prendendo la sua radice quadrata.