caricato da
common.user6158
Riassunto Didattica della Matematica: Numeri Interi Positivi

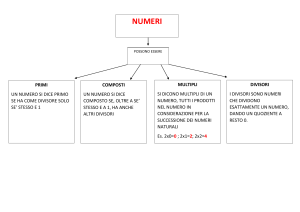
RIASSUNTO ESAME DIDATTICA DELLA MATEMATICA – NICLA PALLADINO- SCIENZE DELLA FORMAZIONE PRIMARIA (UNIPG) Capitolo I: I numeri interi positivi La diversità dei punti di vista, è il risultato di rilevanti ricerche, tutte quante motivate dalla persuasione che trovando una definizione del concetto di numero si sarebbe fatto vedere, tra l’altro, che i teoremi dell’aritmetica sono pure verità logiche e quindi essa poteva essere fondata in modo più sicuro di prima; per conseguenza, ogni altra scienza, riconducibile all’aritmetica, sarebbe stata molto più sincera. Gli Elementi, scritti nel III secolo a.C., rappresentano una collezione organizzata della matematica greca, e perciò riflettono anche tanta parte della matematica caratteristica della scuola pitagorica. Definizione 1 del Libro VII: unità è ciò secondo cui ciascun ente è detto uno. Secondo tale definizione, l’unità sarebbe da intendersi quale “idea” o “concetto” noto a cui la mente umana, nella sua funzione di “concezione” ricorre nel formulare questa definizione. Definizione 2 del Libro VII: numero è una pluralità composta da unità. Tale definizione pare giustificare la proposta del numero da intendersi quale “ripetizione” di unità. Porsi domande sulla natura dei numeri, sulla loro esistenza in toto o su quali numeri esistano è ritenuto un’utile esigenza. Dalla quasi totalità dei matematici è invece assunto che la matematica svolga appieno e correttamente il suo compito dimostrando che i suoi teoremi sono deducibili dai suoi assiomi. Oggi si dice che la matematica “pura” è del tutto ipotetica. Essa si preoccupa prevalentemente di sapere che se certi assiomi sono ammessi come veri, allora è necessario, nel rispetto di una “logica” codificata in astratto, secondo determinate regole, che lo siano anche certi teoremi. Non bisogna preoccuparsi del significato dei termini primitivi che ricorrono negli assiomi o postulati. Questa concezione, che considera i sistemi matematici assiomatizzati come sistemi formalizzati, cioè come “giochi di segni” in cui certe sequenze di segni sono derivabili da altre secondo determinate regole è detta formalismo. Secondo Baker, le formule possono essere interpretate come “verità sul contare”, dove il “procedimento di conteggio” consiste nel pronunciare in sequenza le parole “uno”, “due”, “tre”, ecc…, nel momento in cui si indica una certa sequenza di oggetti. Quando degli oggetti sono individuabili per singole unità allora è possibile contarli. Per farlo si associa un singolo segno al singolo oggetto; una sequenza di segni ripetuti vengono allora associati a più di un oggetto. Una sequenza di segni si dice che costituisce anche una figura numerica (o cifra). Facendo astrazione dalla natura del mucchio di oggetti che si è contato, se alla fine tutti i conteggi risultano figure numeriche della stessa lunghezza allora si dice che esse esprimono lo stesso numero. Quindi il numero è quel qualcosa che è comune a tutte le figure numeriche della stessa lunghezza. L’estensione di una figura numerica (o cifra) corrisponde al valore di un numero. La necessità di percepire immediatamente l’estensione di figure numeriche, ha fatto nascere l’esigenza di sistemi con cui raggrupparne gli elementi: sistema quinario, decimale, ventesimale, sessagesimale. Questa necessità va alla pari col bisogno di dare un nome a ciascun numero, ovvero associare a una data figura numerica una parola che lo contraddistingua in maniera univoca. Questa parola, che è il nome del numero, si dice numerale. Ogni numero potrebbe avere per nome una parola presa a caso. Dato che ciò avrebbe richiesto un notevole sforzo della memoria, si è preferito articolare i nomi dei numeri in corrispondenza al sistema di raggruppamento. Progressivamente, gli uomini pensarono anche a un nome fatto da una sigla, ossia un simbolo. La scelta delle sigle (o simboli) è andata nel corso dei secoli, legandosi in una corrispondenza sempre più stretta con i sistemi di raggruppamento e quindi di numerazione. L’idea che sta a fondamento dei sistemi di numerazione è quella di considerare che un certo gruppo di oggetti, presi tutti insieme, conti come un’unità di ordine superiore, in modo che la numerazione possa ricominciare per proseguire fino all’introduzione di una nuova novità. In queste numerazioni, dette sistematiche, la maniera più semplice di procedere è quella di formare ogni unità con un numero fisso di unità dell’ordine immediatamente inferiore. Questo numero costituisce la base del sistema di numerazione. Una spinta allo sviluppo dei sistemi di numerazione fu data nel momento in cui si cercò di conservare nel tempo il risultato di certe operazioni, e si arrivò alla numerazione scritta. Inizialmente si usarono oggetti infilati al modo di una collana, o nodi fatti su una corda, espedienti che si ridussero successivamente a forme più semplici. L’uso di un sistema di numerazione, comportò che per ogni unità di ordine superiore si venne ad introdurre un nuovo segno. Gli egizi, usavano una numerazione decimale (geroglifici): Per scrivere gli altri numeri si servivano di una legge additiva, ad esempio per scrivere il numero 300, scrivevano tre volte il simbolo del cento. Si pensa che dalla scrittura geroglifica degli antichi egizi, gli scribi abbiano avuto la necessità di raggruppare queste barre mediante segni che le raccogliessero per “fasci”. Per conseguenza venivano a formarsi segni specifici a seconda dei tipi di “fasci” di raccolta; segni che vennero a formare le cifre che rappresentano i numeri da 1 a 9. I greci, grandissimi cultori della geometria, non brillavano, invece, per il modo con cui scrivevano i numeri. Possedevano tre sistemi di numerazione, in base dieci, tutti abbastanza insoddisfacenti. Il primo sistema serviva ai mercanti, che usavano punti o trattini per indicare le unità, i quali venivano poi raggruppati in decine. Il secondo sistema veniva specialmente usato dagli epigrafisti ed era Attico o Erodiano perché esso fu descritto in un frammento attribuito a Erodiano, il quale diceva di aver visto questi segni in un codice che raccoglieva le leggi elaborate da Solone. I segni usati sono sostanzialmente abbreviazioni o raggruppamenti di abbreviazioni. Nel terzo sistema, alfabetico, si utilizzavano come simboli le 24 lettere dell’alfabeto greco più altre tre lettere cadute poi in disuso, in modo da avere in tutto 27 simboli. Di essi, le prime 9 lettere costituivano i simboli delle unità (da 1 a 9) e le successive 9 lettere le decine (da 10 a 90) e le rimanenti le centinaia (da 100 a 900). Per indicare le migliaia (da 1000 a 9000) si usavano le medesime lettere delle unità premettendo però alla sinistra della stessa lettera una sbarra e si procedeva analogamente per le decine di migliaia e così via. Il sistema di numerazione degli egizi, rispetto a quello dei greci, comportava la “memorizzazione” di un numero minore di simboli. Gli egizi, infatti, avevano solo tre simboli per indicare i numeri compresi tra 1 e 1000, numeri che i greci scrivevano adoperando 27 simboli. I romani usavano dapprima, segni convenzionali di origine etrusca, che successivamente vennero identificati con lettere dell’alfabeto. Gli etruschi infatti, utilizzavano una numerazione a base decimale, che si era sviluppata a partire da un primitivo sistema quinario. Il sistema di numerazione dei romani rappresenta una modificazione di quello degli Etruschi . i romani riuscivano a scrivere i numeri, almeno quelli non troppo alti, in modo piuttosto razionale, con meno simboli dei greci e più sinteticamente degli egizi. Quando i simboli si susseguivano da sinistra verso destra, in ordine di valore decrescente, si sommavano. Se una cifra di minor valore precedeva una di maggior valore, allora da quest’ultima si sottraeva quella minore. Per indicare le migliaia essi tracciavano una sbarra orizzontale sopra il simbolo esprimente un numero di ordine inferiore. Le prime tracce storiche del nostro moderno sistema di numerazione risalgono al 500 d.C. e si ritrovano in India, ma la sua origine è sicuramente più remota in quanto, si trovavano elementi posizionali. Il sistema completo con l’uso del metodo posizionale, delle nove cifre e dello zero si trovano nelle opere del matematico indiano del VII secolo Brahmagupta. Una trattazione organica di questo metodo risale al IX secolo e si trova in un trattato di al-Khuwârizmî pubblicato a Baghdad e portato in Europa dai mercanti. Il sistema di numerazione indo-arabico e i metodi di calcolo indiani furono introdotti in Europa da Leonardo Pisano, il Fibonacci, con il Liber Abaci; le forme attuali dei numeri assunte verso i secoli XIV e XV si dicono composte con cifre arabe ed essendo dieci i simboli usati, il sistema di numerazione è decimale. Capitolo 2: Le operazioni sui numeri interi positivi Una delle caratteristiche principali del sistema di numerazione indo-arabico è quella di poter eseguire calcoli scritti. Il vantaggio, determinante, che viene dall’esecuzione per iscritto dei calcoli, è rappresentato dalla controllabilità successiva dei calcoli stessi. Detto per inciso, eseguire calcoli scritti vuol dire mettere colui che calcola in condizione di grande vantaggio rispetto a chi esegua calcoli mentali, oppure fatti con l’ausilio delle mani. L’abilità nel far di conto viene spesso indicata come uno dei fattori che contribuirono ad una rapida espansione e alla supremazia nel commercio dei mercanti arabi e di quelli degli altri popoli che vennero in contatto con loro. Non per niente vi fu, nel corso di alcuni secoli una contrapposizione tra “abacisti” e “algoritmisti”. Per dare, a tal proposito, esempi più antichi e curiosi, si può osservare che operazioni, del tipo di quelle che effettuavano i babilonesi o gli egiziani avevano un’esecuzione diversa da quella moderna. La moltiplicazione e la divisione venivano ricondotti a procedimenti additivi. Essa era seguita come una successione di duplicazioni, seguita da un’addizione. Allo stesso modo la divisione si riduceva a dimezzamenti successivi. In generale, la moltiplicazione veniva eseguita scegliendo uno dei due fattori che, posto nella colonna di destra, veniva duplicato successivamente, mentre nella colonna di sinistra si riportavano le successive potenze di 2; di queste potenze si individuavano quelle la cui somma dava l’altro fattore e il risultato della moltiplicazione si otteneva sommando i termini corrispondenti a tali potenze. L’idea generale era quella di prendere i multipli o le parti di 8 che sommate davano 19. Va osservato che gli egiziani non usavano frazioni con numeratore maggiore di 1, ad eccezione della frazione 2/3 per la quale esisteva uno speciale geroglifico ma eseguivano i calcoli sulla base di frazioni con numeratore 1, le quali rappresentano ciascuna il reciproco di un numero intero positivo. Di conseguenza una qualsiasi frazione veniva espressa come somma di unità frazionarie differenti. L’abaco da considerarsi, forse, la prima macchina per calcolare, si ritrova, in una forma o nell’altra praticamente in tutti i paesi in cui è esistita una tecnica di calcolo non più primitiva. Il poeta latino Orazio nelle Satire, scriveva che i bambini andavano a lezione reggendo con il braccio di sinistra la borsa e la tavoletta cerata per scrivere. L’abaco ha costituito per millenni il solo strumento di rappresentazione posizionale dei numeri, prima che si pervenisse alla scrittura posizionale. Ad esempio i romani utilizzavano l’abaco per rappresentare concretamente i numeri e per eseguire le relative operazioni. Si può partire dallo stesso termine abaco per fare delle ipotesi sulle sue origini. Molti ritengono che la radice del termine derivi dalla parola semitica abaq (polvere). Tale vocabolo sarebbe stato in seguito adottato dai greci che a loro volta avrebbero utilizzato il termine abax per indicare una superficie piana o un tavolo sul quale tracciavano le righe necessarie per i calcoli. La parola sarebbe poi diffusa tra i romani che denominarono la loro tavola abacus. Nella sua forma generale più semplice, l’abaco consiste in una tavoletta, divisa in una serie di guide parallele, ciascuna delle quali rappresenta una diversa classe decimale. La tavola è provvista di un certo numero di palline o simili oggetti, che servono per indicare il numero delle unità di ciascuna classe. Per indicare un numero senza equivoci bisognava dire se qualche casella dell’abaco era vuota e quale. Per questo motivo, si rivelò necessario l’uso di un mezzo che rappresentasse i vuoti, un simbolo cioè che indicasse una casella vuota: lo zero. Quest’idea venne dall’India ed è la caratteristica principale del sistema indo-arabico. Gli indiani introdussero un simbolo per il vuoto e lo chiamarono sunya, che vuol dire “vuoto”. Gli arabi tradussero l’indiano sunya con la loro parola sifr. Tale parola araba acquistò nell’Europa medievale due significati diversi: da un lato, il significato generico di segno per indicare un numero, divenne cioè la nostra cifra; dall’altro, trasformata prima in zephyrum, poi in zevero, infine in zero, indicò la cifra per eccellenza, il simbolo del “nulla”. Con l’introduzione di un decimo simbolo, 0, e di un decimo numero, lo zero, divenne naturale fare a meno degli abachi e scrivere tutti i numeri possibili come una sequenza di segni (cifre), come una parola scritta usando un alfabeto con dieci lettere. Per definizione, un’operazione in un insieme è rappresentata da una “legge di composizione”, che ad ogni coppia di elementi dell’insieme, detti operandi, ne associa un altro detto risultato. Dato che gli elementi dell’insieme “messi in relazione” dalla “legge” sono due allora si parla di relazione binaria. Se, comunque si scelgano gli elementi a e b della coppia, il risultato c appartiene ancora all’insieme, l’operazione è detta interna all’insieme, e lo stesso insieme si dice chiuso rispetto all’operazione. Addizione L’operazione di addizione nell’insieme dei numeri interi positivi, al quale è aggiunto lo zero, è regolata dalla “legge di composizione”. “Addizionare due numeri a e b vuol dire accrescere il numero a di tante unità quante sono indicate da b. il numero che si ottiene è il risultato dell’operazione”. L’operazione di addizione definita sull’insieme N0, risulta interna all’insieme stesso, ossia, comunque siano presi due numeri appartenenti ad N0, la loro somma è ancora un numero di N0. I numeri a e b sono gli addendi, mentre il risultato dell’operazione, c, è la somma. Per l’addizione in N0 valgono le seguenti proprietà fondamentali: Commutativa: cambiando l’ordine degli addendi il risultato non cambia. Associativa: nella somma di tre o più addendi non ha importanza l’ordine con il quale si eseguono le addizioni. Esistenza dell’elemento neutro: denotato con 0; per ogni elemento a dell’insieme si ha sempre: a + 0 = a. Il Fibonacci, nel suo Liber Abaci, espone le 4 regole per eseguire le 4 operazioni fondamentali dell’aritmetica. Sottrazione La sottrazione tra due numeri a e b appartenenti all’insieme N0, è definita come operazione inversa dell’addizione; vale a dire, “il risultato è rappresentato da quel numero c che, sommato a b, eguaglia a”. Il termine a è detto minuendo, il termine b sottraendo, mentre il risultato c dell’operazione è la differenza. La sottrazione non è, nell’insieme dei numeri denotati con N0, un’operazione interna. Infatti , non è certo che, dati due numeri qualsiasi appartenenti ad N0, la loro differenza sia ancora un numero dell’insieme: ciò accade quando il sottraendo risulta essere maggiore del minuendo, se accade ciò questi numeri, detti numeri interi relativi, si indicano con il simbolo Z che è l’iniziale della parola tedesca Zahl (Zahlen, plurale) che vuol dire numero (numeri). Per la sottrazione in N0 valgono le seguenti proprietà: Esistenza dell’elemento neutro: 0, preso un qualsiasi elemento dell’insieme, si ha sempre che: a – 0 = a. Invariantiva: la differenza c tra a e b non cambia se si aggiunge o si toglie (in questo caso, solo quando è ammesso) uno stesso numero d rispettivamente a minuendo e sottraendo. Moltiplicazione La moltiplicazione di due numeri a e b di N0 è definita come la somma di b addendi tutti uguali ad a. I termini a e b sono detti fattori (il primo si chiama moltiplicando, il secondo moltiplicatore), mentre il risultato c dell’operazione è il prodotto. Tale operazione, definita sull’insieme N0, risulta interna all’insieme stesso vale a dire che comunque presi due numeri naturali il loro prodotto è ancora un numero naturale. Per la moltiplicazione valgono le seguenti proprietà: Commutativa: cambiando l’ordine dei fattori il prodotto non cambia. Associativa: nel moltiplicare tre o più fattori non ha importanza l’ordine con il quale si eseguono le moltiplicazioni. Distributiva della moltiplicazione rispetto all’addizione: moltiplicare un numero per una somma equivale a moltiplicarlo per ciascun addendo e ad addizionare i prodotti così ottenuti. La stessa proprietà vale anche nel caso della sottrazione. Esistenza dell’elemento neutro: denotato con 1; per ogni elemento a dell’insieme, si ha sempre che: a 1 = a. Legge di annullamento del prodotto: il prodotto di più fattori è uguale a zero se almeno uno di essi è zero e viceversa: a b 0 c = 0. Nel 1614, Nepero costruì un metodo, basato su “bastoncini” o “regoli”, che serviva per effettuare in modo elementare moltiplicazioni e divisioni. Materialmente, il dispositivo era costituito da una serie di regoli rettangoli, allungati come bacchette ognuno dei quali era contrassegnato da un numero compreso tra 0 e 9 scritto in cima e dai suoi multipli distribuiti in caselle dalla forma quadrata disposte lungo tutta la lunghezza del “bastoncino”. Vi era poi un altro “bastoncino”, chiamato “guida”, numerato da 0 a 9 che, posto accanto agli altri, indicava il numero della riga orizzontale su cui si operava. La scelta delle caselle quadrate rendeva possibile affiancare facilmente un “bastoncino” all’altro. Ciascuna delle nove caselle disegnate sui “bastoncini” era divisa, mediante la sua diagonale, in due triangoli uguali; mediante i bastoncini era possibile eseguire moltiplicazioni con fattori di un numero qualsiasi di cifre. Ad un principio analogo a quello dei “bastoncini di Nepero” si ispira l’algoritmo per il calcolo del prodotto, che lo avevano denominato gli arabi “a caselle” o a “reticolo”. In Italia tale metodo era detto “a gelosia”. Rafael Bombelli, nell’opera L’Algebra, edita per la prima volta nel 1572, che rappresenta la summa delle conoscenze algebriche disponibili fino alla seconda meta del 1500, usava il termine “via” per indicare il segno di moltiplicazione equivalente all’attuale “per”. Ad esempio: se si moltiplicherà 4 via 9 il prodotto sarà 36. Divisione La divisione fra due numeri a e b, di N0, (con b diverso da 0), è definita come operazione inversa della moltiplicazione; vale a dire il risultato è rappresentato da quel numero q, che moltiplicato per b uguagli a. il termine a è detto dividendo, il termine b divisore, il risultato q dell’operazione è il quoziente. La “divisibilità” di a per b, non sempre è assicurata; nel caso in cui non sia verificata, si può eseguire la “divisione con resto” di a per b, ossia, cercare due numeri naturali q ed r tali che accada: a = b q + r dove con r è indicato il resto, che soddisfa la relazione 0 r b. Talvolta si utilizza la parola quoto per indicare il risultato della divisione nel caso in cui il resto è nullo, mentre si utilizza la parola quoziente per indicare il risultato della divisione nel caso in cui il resto non è nullo. L’operazione di divisione tra due numeri interi non è interna all’insieme N0 e nemmeno all’insieme Z, ma porta a considerare un nuovo insieme, fatto di quozienti, denotato con Q. Per provare la validità della relazione: 0 r b, si procede distinguendo due possibili casi: Se a è multiplo di b, allora dalla divisione di a per b si ottiene: a = q b e r = 0, con q numero intero positivo, quindi la relazione è soddisfatta; Se a è compreso tra due multipli successivi di b, cioè: b q < a < b (q + 1) = b q + b, applicando alla precedente la proprietà invariantiva si ottiene: 0 < a – b q = r < b e la relazione risulta soddisfatta. Il procedimento adoperato da Euclide negli Elementi, aveva come scopo il calcolo del massimo comune divisore tra due interi positivi: Se a < b, allora q = 0 ed r = a; Se a b, allora si sottrae b da a tante volte quant’è necessario perché il resto diventi più piccolo di b. il quoziente q si ottiene costando quante volte b è stato sottratto da a. Per la divisione valgono le seguenti proprietà: Invariantiva: moltiplicando o dividendo i due termini di una divisione per uno stesso numero, diverso da zero, il quoziente non cambia e il e il resto risulta moltiplicato per quello stesso numero; Proprietà distributiva della divisione rispetto all’addizione: dividere una somma per un numero c è equivalente a dividere ciascun addendo per c e addizionare i quozienti ottenuti. La stessa proprietà vale anche nel caso della sottrazione. Prendiamo ora in considerazione la cosiddetta “prova del nove” storicamente utilizzata per controllare l’esattezza della moltiplicazione eseguita tra due numeri naturali. Essa è applicabile a tutte e quattro le operazioni fondamentali dell’aritmetica. Se dà esito negativo, vuol dire che nell’eseguire i calcoli sono stati fatti degli errori e dunque occorre ripetere l’operazione corrispondente. La “prova” si effettua con i seguenti passaggi tramite uno schema a croce: Si sottraggono dal moltiplicando tutti i possibili 9; si ottiene quale differenza finale il “resto” n (1^ casella a sinistra in alto). Si sottraggono dal moltiplicatore, tutti i possibili 9, si ottiene quale differenza finale il “resto” n (2^ casella a destra in alto). Si moltiplicano i due “resti” e cioè il 3 e il 2, e dal risultato si sottraggono tutti i 9 possibili, si ottiene il “resto” n (3^ casella a sinistra in basso). Si sottraggono dal prodotto della moltiplicazione, tutti i possibili 9, si ottiene quale differenza finale il “resto” n (4^ casella a destra in basso). La “prova del nove” fornisce in matematica una condizione necessaria ma non sufficiente. Alla base della “prova del nove” vi è l’operazione di congruenza. In generale dati due numeri a e b si dice che essi cono congrui modulo m se sottraendo da a e da b tutti gli m possibili si ottiene la stessa differenza finale (“resto”). Capitolo 5: I numeri primi Un numero intero positivo o “naturale” n, eccettuato il numero 1, che abbia come divisori solo 1 e se stesso, è detto numero primo. Euclide nella definizione 11 del Libro VII degli Elementi afferma: numero primo è quello che è misurato soltanto dall’unità. Per i numeri primi vale il Teorema fondamentale dell’aritmetica: ogni numero intero maggiore di 1 è scomponibile in un unico modo come un prodotto di numeri primi. Un numero intero (diverso da 1) che non sia primo si dice numero composto. Nella proposizione 20 del Libro IX degli Elementi, Euclide dimostra che la successione dei numeri interi primi è illimitata: esistono numeri primi in numero maggiore di quanti numeri primi si voglia proporre. Per dimostrare questa proposizione Euclide suppone che siano dati tre numeri primi qualsiasi a, b, c; egli fa vedere che esiste almeno un quarto numero primo diverso da ciascuno di questi tre. A tale scopo, conducendo la dimostrazione con moderno simbolismo, si moltiplicano tra loro i tre numeri dati e si aggiunge una unità, ottenendo così il numero: d = abc + 1 maggiore di ciascuno dei tre. Se d è primo, esso allora è un altro numero primo “esistente” nella visione euclidea, e perciò va ad aggiungersi ai tre dati a, b, c. Se d non è primo, esso ammette almeno un divisore primo, diverso da 1 (proposizione 31 del Libro VII degli Elementi) che si vuole indicare con h. Il numero h è diverso da a, b, c, perciò esso costituisce il un quarto numero primo. La dimostrazione dell’illimitatezza della successione dei numeri primi è collegata a una pratica molto semplice per costruire una successione di infiniti primi, progressivamente sempre più grandi. Tali numeri si ottengono aumentando, di volta in volta, di un’unità i prodotti dei numeri primi, consecutivi, a partire da 2. Con questo procedimento però non si ottengono tutti i numeri primi compresi fra 2 ed un numero assegnato, per questo si fa riferimento al procedimento noto come Crivello di Erastotene in cui si trattano tutti i numeri primi minori di n. Per mettere in pratica questo procedimento: Si scrivano i numeri naturali in successione (ad esempio i numeri naturali da 2 a 100 in una tabella). Nel primo passo si tolgono tutti i multipli di 2. Nel secondo passo si tolgono tutti i multipli di 3. Nel terzo passo si tolgono tutti i multipli di 5. Nel quarto passo si tolgono tutti i multipli di 7 e così via. Alla fine i numeri che sono rimasti nella lista, dopo aver “setacciato e messi via” tutti i numeri composti, sono primi. Non si è ancora riusciti a studiare un criterio, e quindi un algoritmo, che consenta di determinare a priori la distribuzione dei numeri primi all’interno dell’insieme dei numeri naturali. Infatti, uno dei più antichi problemi riguardanti i numeri primi consiste nel fatto che nessuno mai è riuscito a trovare una formula o un sistema che permettano di determinare se un numero è primo o no. L’etimologia della parola “crittografia” deriva dalle parole greche kriptos = nascosto e graphos = scrittura, quindi crittografia vuol dire scrittura segreta. La crittografia tradizionale richiedeva l’uso di una chiave segreta da concordarsi riservatamente, dal punto di vista pratico. A partire dagli anni Settanta del XX secolo si sono affermati i cosiddetti cifrari a chiave pubblica basati su una filosofia del tutto diversa: la chiave per cifrare non è la stessa di quella per decifrare. Per questo motivo sono detti anche cifrari asimmetrici. Il sistema di crittografia a chiave pubblica più noto è il sistema RSA, dalle iniziali degli autori Rivest, Shamir e Adleman che lo hanno inventato nel 1978, e si basa sull’enorme differenza tra la facilità di trovare numeri primi grandi e la difficoltà di scomporre in fattori il prodotto di due numeri primi grandi. Tale sistema permette con l’uso dei numeri primi, la comunicazione sicura di informazioni in tutto il mondo. Capitolo 6: Scomposizione in fattori primi Scomporre un numero intero positivo in fattori primi significa trasformarlo in un prodotto di numeri primi. Ciò è possibile per qualsiasi numero n, non primo, poiché esistono sempre due numeri a e b tali che: n = a x b. Se i due numeri a e b non sono ancora dei numeri primi, possono ulteriormente scomporsi fino a pervenire alla scrittura del numero n in un prodotto di fattori primi. L’importanza dei numeri primi nella scomposizione di un numero in fattori, sta nel fatto che essi permettono di rivelare l’intima struttura di un numero composto. I numeri primi si possono anche vedere allo stesso modo delle lettere dell’alfabeto allorché si compongono le parole di un linguaggio letterario. Con la proposizione 31 del Libro VII degli Elementi di Euclide, Euclide dimostra il seguente teorema sul quale si fonda la scomposizione di un numero in fattori primi: ogni numero composto ha per divisore un numero primo. Con la proposizione 30 del Libro VII è dato un teorema che permette di dedurre l’univocità della suddetta scomposizione: se due numeri si moltiplicano tra loro, ed un altro numero, che sia primo, divide il prodotto, esso dividerà anche uno dei fattori. Quando si è espresso un numero come prodotto di primi, si possono disporre i suoi fattori in ordine qualsiasi; la scomposizione in fattori primi di un numero è unica, ovvero, è regolamentata dal Teorema fondamentale dell’aritmetica: ogni numero n, maggiore di 1, può essere scomposto in modo unico in un prodotto di primi. Heath nel suo libro A History of Greek Matemathics, fa notare che tale proposizione che risulta equivalente a questo importante teorema si trova nel Libro IX degli Elementi di Euclide; si tratta della proposizione 14 che dice: se un numero, che sia il più piccolo possibile, è diviso da certi numeri primi, esso non sarà diviso da nessun altro numero eccetto quelli che inizialmente ne siano divisori. La scomposizione di un numero non primo in fattori primi si esegue nel seguente modo: Si determina se il numero è divisibile per 2 e in caso affermativo si calcola il quoziente; Si prosegue determinando se il quoziente è divisibile ancora per 2; Si esegue la divisione iterando il procedimento finché si trova un quoziente non più divisibile per 2; Verificato che il numero di partenza o l’ultimo quoziente non è divisibile per 2 si ripercorrono i passi precedenti per il numero 3; E così via finché si giunge ad un quoziente espresso da un numero primo. Un modo per “ fattorizzare con carta e penna” un generico numero è quello di applicare i criteri di divisibilità. Capitolo 7: Divisori di un numero Considerato un numero intero positivo n, si definiscono suoi divisori quei valori interi di (elementi dell’insieme dei divisori) tali che la divisione di n con ciascuno dei di abbia come resto zero. I divisori di tale n sono in numero limitato e fra di essi non mancano mai 1 e n stesso, vale a dire che ogni numero maggiore di 1 ammette come divisori almeno l’unità e il numero stesso. Per ogni numero naturale n 2, sia D(n) il numero dei suoi divisori, compresi l’unità e il numero stesso. Il matematico indiano Ramanujan, ha dato una definizione concernente i numeri godenti di particolari proprietà rispetto ai propri divisori. Egli ha definito altamente composto un numero n tale che per ogni naturale m, con 2 m n, risulta: D(m) < D(n). Per stabilire se un numero intero n è divisibile per un certo di, è sufficiente eseguire la divisione di n per di e vedere se il resto dell'operazione è uguale a zero. Esistono, però, alcune regole pratiche che consentono di stabilire in anticipo, senza alcuna divisione, se un numero è divisibile per un altro. La storia di queste regole affonda le sue radici in epoche molto antiche. Forse gli Arabi fecero conoscere all’occidente alcuni di questi metodi, importandoli dall'India insieme alle cifre moderne con cui si rappresentano i numeri nel sistema decimale. Capitolo 8: Massimo Comune Divisore Il Massimo Comune Divisore (M.C.D.) tra due o più numeri interi positivi è il più grande numero che sia contemporaneamente divisore di tutti i numeri dati. Ci sono diverse procedure che permettono di calcolare questo valore, tra cui, l’algoritmo per ottenere il Massimo Comune Divisore tra due o più numeri, che viene esposto da Euclide nelle prime tre proposizioni del Libro VII degli Elementi. Nella prima proposizione viene trattato il caso particolare dei numeri interi positivi primi tra loro, Tale proposizione permette, infatti, di stabilire se due numeri sono primi tra loro, ovvero se il loro M.C.D. è uguale a 1. Essa afferma: se si prendono due numeri disuguali e si procede (a sottrazioni successive), togliendo di volta in volta il minore dal maggiore, (la differenza dal minore e così via), se il numero che (ogni volta) rimane non divide mai quello che immediatamente lo precede, finché rimanga soltanto l’unità, i numeri dati dall’inizio saranno primi tra loro. In pratica si procede così: Dati due numeri, a e b, si effettua la loro differenza a - b = d; Dei tre numeri a (minuendo), b (sottraendo), d (differenza), si mette da parte il più grande, a; Considerati poi gli altri due, b e d, sì effettua la differenza tra di loro (togliendo, ovviamente, il minore dal maggiore); Si procede così per passi successivi sempreché il numero che esprime la differenza ottenuta nel singolo passo non divida il relativo minuendo; Se si perviene ad avere come differenza l’unità, allora i due numeri sono primi tra loro. Si consideri, ora, la determinazione del M.C.D. tra due numeri, non primi tra di loro, utilizzando ancora l'algoritmo euclideo delle sottrazioni successive. A tal fine la proposizione 2 del Libro VII degli Elementi dice: dati due numeri che non siano primi fra loro, trovare il loro massimo comune divisore. La corrispondente procedura viene presentata, da Euclide, applicando il precedente algoritmo delle sottrazioni successive. Infatti, considerati due numeri a e b, si procede con le sottrazioni ripetute, fin quando, ad un certo passo, non si avrà una differenza che dividerà il relativo sottraendo; tale differenza è il M.C.D. cercato. Dal metodo di Euclide che opera mediante le sottrazioni successive deriva una procedura, per il calcolo del M.C.D. fondata sulla constatazione che la divisione tra due numeri può essere interpretata come sottrazione ripetuta. Essa, denominata, dagli studiosi algoritmo euclideo delle divisioni successive, è formulabile al modo seguente: se si prendono due numeri disuguali e si dividono tra di loro e si procede poi a divisioni successive tra ciascun divisore e il relativo resto, e se il resto che di volta in volta rimane non divide mai il relativo divisore, finché rimanga soltanto l’unità, i numeri dati all'inizio saranno primi tra loro. Di conseguenza: per calcolare il massimo comune divisore di due numeri, non primi tra di loro, si eseguono le divisioni nel modo anzidetto e si prende, per M.C.D., il primo resto, che si viene ad incontrare, che divida il relativo divisore. A questo proposito, il matematico francese Gabriel Lamé dimostrò che: il numero di divisioni necessarie per determinare il massimo comune divisore di due numeri è al più cinque volte il numero delle cifre del numero più piccolo. Al metodo delle sottrazioni successive i libri scolastici preferiscono tuttavia un procedimento per calcolare il M.C.D. tra due numeri, basato sul concetto di fattorizzazione di un numero composto. Il metodo consiste nello scomporre i numeri in prodotto di fattori primi e individuare i fattori comuni con il minimo esponente, il M.C.D, sarà il prodotto di tali fattori; alternativamente, si possono calcolare i divisori di tutti i numeri dati, verificare quali sono i divisori comuni e il più grande di questi è il M.C.D. Per quanto riguarda il M.C.D. si osservi, infine, che vale anche la seguente proprietà: se due numeri sono uno multiplo dell’altro, il loro massimo comune divisore è il minore di essi. Capitolo 9: Minimo Comune Multiplo Il minimo comune multiplo (m.c.m.) di due o più numeri è il più piccolo numero che sia multiplo di tutti i numeri dati. Anche il calcolo del minimo comune multiplo tra due o più numeri viene esposto da Euclide nel Libro VII degli Elementi, rispettivamente nelle proposizioni 34 e 36. Euclide usa, per indicare il m.c.m. tra numeri, l'espressione “il numero più piccolo che essi dividano”. Per calcolare il minimo comune multiplo fra due o più numeri si scompongono preliminarmente i numeri in fattori primi, il m.c.m. si ottiene facendo il prodotto dei fattori primi comuni e non comuni presi una sola volta, col massimo esponente. Quando si tratta di calcolare il m.c.m. di più numeri è conveniente comporre simultaneamente i numeri in fattori primi. Si può osservare che: se due numeri sono primi tra loro, il minimo comune multiplo è il loro prodotto. Per conseguenza, essendo due numeri consecutivi primi tra loro, si ha: il minimo comune multiplo di due numeri consecutivi è il loro prodotto. Vale, infine, la seguente proprietà: se due numeri sono uno multiplo dell'altro, il minimo comune multiplo è il maggiore di essi. Si noti, inoltre, che il m.c.m. tra due numeri si può ottenere attraverso il calcolo del M.C.D. tra gli stessi due numeri; infatti, vale la proprietà: il minimo comune multiplo di due numeri si calcola dividendo uno dei numeri per il loro massimo comun divisore e moltiplicando il quoziente per l'altro numero. Capitolo 12: I numeri di Fibonacci Successione numerica: è un insieme ordinato di numeri, tali che ciascuno occupa un posto stabilito (connotato, in generale, da un indice), in modo da poter individuare il primo, il secondo, il terzo e così via. I numeri di Fibonacci sono costituiti da una successione matematica, i cui elementi e i cui rapporti si riscontrano in una straordinaria varietà di fenomeni naturali e artistici. Alla successione: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... fu dato il nome del suo scopritore duecentesco, Leonardo Pisano (detto il Fibonacci) che in una sezione del suo famoso trattato, Liber Abaci, poneva un problema matematico: se una coppia di conigli rimane isolata, quanti conigli nasceranno nel corso di un anno, ammesso che ogni mese una coppia di conigli ne produca un'altra coppia, e che i conigli incomincino a partorire due mesi dopo la propria nascita? Alla fine del decimo mese si ritrovano 89 coppie di conigli mentre alla fine dell’anno 233 coppie. La regola di forma i formazione dei numeri di Fibonacci, ispirata da questo problema è: il generico numero (a partire dal secondo), denotato con Fibn, si ottiene eseguendo l'addizione dei due numeri che lo precedono nella successione. Espresso in formula: Fibn = Fibn-1 + Fibn-2 dove: Fibn = n = 0 → Fib0 = Fib1 = 1 (posizioni 0 e 1 sempre 1) La successione di Fibonacci gode delle seguenti proprietà: Il quadrato di ogni numero di Fibonacci differisce di un'unità dal prodotto dei due numeri posti di fianco ad esso nella successione. La differenza è, alternativamente, positiva o negativa, via via che si avanza nella successione. Sommando i primi n numeri della successione di Fibonacci ed aggiungendo un'unità, il risultato è sempre uguale al numero di posto (n + 2) della successione stessa. Se invece di sommare tutti i numeri, nessuno escluso, fino all'n-mo della successione di Fibonacci, se ne somma uno si ed uno no, il risultato è sempre uguale al valore dell'(n + 1)-mo numero della medesima successione. Se si prendono due numeri di Fibonacci consecutivi e se ne fa di ciascuno il quadrato, allora la somma fra i quadrati è un altro numero di Fibonacci che nella successione occupa il posto risultante dalla somma delle posizioni dei due termini di partenza. Considerati quattro numeri di Fibonacci consecutivi qualsiasi, a, b, c, d, allora è sempre valida la relazione: c2 – b2 = a d. A parte il caso banale dello zero e dell’uno, l'unico numero di quadrato perfetto è Fib (12) = 144. L'unico cubo è Fib (6) = 8. Il Massimo Comune Divisore di due numeri a e b, facenti parte della successione di Fibonacci, risulta essere ancora un numero di Fibonacci. La frequenza con cui in natura si presenta la successione di Fibonacci è veramente notevole: il numero delle spirali delle brattee delle pigne, quello delle scaglie dell'ananas, o delle rigature interne di una conchiglia sono, molto spesso, numeri di Fibonacci. Capitolo 13: Sezione aurea Euclide, negli Elementi, propone più volte l'argomento “sezione”, ispirato in parte da studi precedenti dovuti ad Eudosso di Cnido. Il primo incontro si ha nel Libro II degli Elementi in cui egli insegna a costruire la “parte aurea” di un segmento attraverso la risoluzione del problema di equivalenza espresso dalla proposizione 11: dividere una retta data in modo tale che il rettangolo compreso da tutta la retta e da una delle parti sia uguale al quadrato della parte rimanente. Il problema, consiste nell'individuare su un segmento dato, AB, un punto H in modo che il rettangolo di lati AB e HB sia equivalente al quadrato di lato AH. Nel Libro VI degli Elementi, dedicato alle applicazioni della teoria delle proporzioni alla geometria piana, la terza definizione afferma: si dice che una retta risulta divisa in estrema e media ragione, quando tutta quanta la retta sta alla parte maggiore di essa come la parte maggiore sta a quella minore. Nella proposizione 30 del medesimo libro (Dividere in estrema e media ragione una retta terminata data), Euclide indica il metodo per individuare il punto che soddisfa la condizione richiesta. La definizione, che si trova negli Elementi di Euclide, fu adottata da tutti gli studiosi come la più autentica espressione del concetto di sezione aurea. Infatti quando di un segmento si determina la sua parte aurea, si dice anche che si è diviso il segmento in media ed estrema ragione. Quindi, geometricamente, dividere un segmento in sezione aurea o in media ed estrema ragione, significa dividerlo in due parti tali che la maggiore sia media proporzionale fra l’intero segmento e la parte rimanente. Ossia, dato un segmento AC di una certa misura, si ottiene una sezione aurea quando il tratto più corto BC sta al tratto più lungo AB come quest’ultimo sta al segmento intero AC. Si supponga che la lunghezza dell’intero segmento sia pari all'unità inoltre, ricordando la proprietà fondamentale delle proporzioni secondo cui il prodotto dei termini estremi è uguale al prodotto dei medi. La sezione aurea è legata alla successione di Fibonacci. Infatti il rapporto fra due numeri di Fibonacci consecutivi tende ad avvicinarsi, con il crescere dei numeri, sempre più al valore del rapporto aureo: 1,618... I greci sostenevano che la natura e l'arte dovevano la loro bellezza a certe leggi matematiche in esse implicite, tra le quali vi era la sezione aurea. I greci la utilizzarono per edificare il Partenone di Atene, la cui facciata orientale è contenuta in un rettangolo d'oro che ne determina l’evidente armonia. Anche il grande scultore greco Fidia se ne servì spesso nella realizzazione delle sue sculture: per questo il rapporto aureo è chiamato φ (phi), dall'iniziale del suo nome. In geometria, la sezione aurea è la chiave per la costruzione del pentagono regolare. I pitagorici, studiando la sezione aurea, scoprirono che il lato del decagono regolare inscritto in una circonferenza di raggio r è la sezione aurea del raggio. Congiungendo un vertice si e uno no del decagono regolare si ha un pentagono regolare. Se si prosegue in questa forma alternata di congiungere i vertici del pentagono regolare, prima ottenuto, si ha la cosiddetta stella a cinque punte o pentagramma, che si può considerare come una sorta di pentagono intrecciato. Il pentagramma fu scelto dai pitagorici quale simbolo dell’armonia segno di riconoscimento della setta. Il lato del pentagono regolare è la sezione aurea di una sua diagonale e il punto d’intersezione tra due diagonali divide ciascuna di esse in due segmenti che stanno nel rapporto aureo. Il rapporto fra una qualsiasi diagonale ed il lato è proprio uguale al numero aureo, così come lo è anche il rapporto fra le parti in blu e quella in rosso della diagonale. La sezione aurea, appare nella simmetria pentagonale di certi fiori e di alcuni animali marini, nelle proporzioni del corpo umano e così via. L’uomo l’ha usata nelle arti e nella tecnica, specialmente nelle attività tipografiche e pubblicitarie. A partire dal Rinascimento la Sectio Aurea acquista il crisma della bellezza estetica. Secondo Luca Pacioli ed Albrecht Dürer (1471-1528), la Sectio Aurea, era elemento proporzionale analogico tra la figura umana e la natura oggettiva. In passato, nelle arti si ricorreva spesso alla la divina proportione, considerata quasi la chiave mistica dell'armonia nelle arti e nelle scienze. Un largo contributo alla conoscenza ed alla divulgazione di questo metodo di suddivisione armonica è stato dato da Luca Pacioli con la pubblicazione nel 1509 del libro De divina Proportione, le cui figure furono disegnate da Leonardo Da Vinci, dedicato allo studio del numero d’oro e delle sue proprietà. Capitolo 16: I numeri geometrici Numeri triangolari Si chiamano numeri triangolari i numeri che, raffigurati al modo pitagorico, assumono la forma di un triangolo equilatero. Essi sono: 1, 3, 6, 10, 15, 21, 28 e così via, Questa disposizione spinse, i matematici della scuola pitagorica ad osservare che la successione dei numeri triangolari si poteva ottenere sommando stringhe di numeri naturali successivi disposte al modo seguente: 1 1+2=3 1+2+3=6 1+2+3+4=10 1+2+3+4+5=15 1+2+3+4+5+6=21 1+2+3+4+5+6+7=28 1+2+3+4+5+6+7+8=36 1+2+3+4+5+6+7+8+9=45 1+2+3+4+5+6+7+8+9+10=55 Per ottenere l’n-esimo numero triangolare Tn si può ricorrere alla formula: 𝐧(𝐧+𝟏) Tn = 2 Che corrisponde proprio a quella usata per il calcolo della somma dei primi n numeri naturali e che si è utilizzata per dare un esempio di applicazione del “Principio d’Induzione”. Si può sottolineare una proprietà legata ai numeri triangolari: ogni numero intero si può scrivere come somma di non più di tre numeri triangolari. I numeri triangolari si possono ottenere anche con procedura ricorsiva utilizzando la formula: Tn+1 = Tn + n+1, dove T0 = 0 Numeri quadrati Si chiamano numeri quadrati i numeri che raffigurati al modo pitagorico, formano un quadrato. Essi sono: 1, 4, 9, 16, 25 e così via. Per passare da un numero quadrato al successivo i pitagorici utilizzavano un metodo grafico consistente nell’addizionare un altro punto per ciascuno dei due lati del quadrato di partenza e nell’aggiungere poi tanti punti quanti erano necessari per formare un nuovo quadrato. Il numero quadrato n-esimo, Qn, si ottiene dalla formula: Qn = n 2 infatti: 1 1 = 1 = 12 2 2 = 4 = 22 3 3 = 9 = 32 Le prime proposizioni dell’opera Liber Quadratorum (1225), cioè il “Libro dei numeri quadrati”, di Leonardo Pisano (il Fibonacci) riguardano ‘il calcolo dei numeri quadrati come somme della successione di numeri dispari: l’n-esimo numero quadrato si ottiene come somma dei primi n numeri dispari; cioè: 1+3+5+7+...+(2n-1)=n2 dove (2n - 1) è la forma di un generico numero dispari. In maniera del tutto equivalente, se al primo numero quadrato aggiungiamo il secondo numero dispari si ottiene il secondo numero quadrato; se al secondo numero quadrato aggiungiamo il terzo numero dispari si ottiene il terzo numero quadrato, e così via. A partire dalla costruzione dei numeri quadrati mediante la successione di numeri dispari, il Fibonacci riuscì a ricavare coppie di numeri quadrati aventi per somme dei numeri quadrati, le misure dei due cateti e dell’ipotenusa di triangolo rettangolo. Osservando la forma figurata dei numeri quadrati, i pitagorici dedussero che ciascun numero quadrato (maggiore di 1) si poteva ottenere anche dalla somma di due numeri triangolari successivi. Tale procedimento, che permette di costruire i numeri quadrati, suggerisce un metodo per estrarre la radice quadrata di un quadrato perfetto. Si abbia, ad esempio, da estrarre la radice quadrata di 81. Da 81 si sottraggono tutti i numeri dispari secondo la successione: 1, 3, 5, … fino a pervenire alla differenza zero. 81 – 1 = 80 80 – 3 = 77 77 – 5 = 72 72 – 7 = 65 65 – 9 = 56 56 – 11 = 45 45 – 13 = 32 32 – 15 = 17 17 – 17 = 0 È possibile applicare lo stesso procedimento anche all'estrazione approssimata della radice quadrata di un numero che non sia un “quadrato perfetto”. In questo caso si registra la presenza di un resto. Si osservi, inoltre, che ogni numero triangolare moltiplicato per 8 e con l'aggiunta di 1 corrisponde ad un numero quadrato. I numeri quadrati si possono ottenere anche con procedura ricorsiva utilizzando la formula: Qn+1 = Qn + (2n + 1), dove si pone Q0 = 0 Numeri pentagonali Sono detti pentagonali i numeri che, raffigurati al modo pitagorico, formano un pentagono regolare. Essi sono: 1, 5, 12, 22 e così via. I numeri pentagonali si ottengono con la formula: 𝐧(𝟑𝐧−𝟏) Pn = 2 Questi numeri godono della proprietà: l’n-esimo numero pentagonale è uguale a n più tre volte l’(n-1)esimo numero triangolare. Si osservi che i numeri pentagonali si possono ottenere anche mediante una procedura ricorsiva utilizzando la formula: Pn+1 = Pn + (3n + 1), dove P0 = 0 Numeri esagonali Esagonali sono detti quei numeri che, raffigurati al modo pitagorico, si dispongono secondo la forma di un esagono regolare. Essi sono: 1, 6, 15, 28 e così via. Una formula per ottenere numeri esagonali è: En = n(2n – 1) Essa viene fuori dall’osservazione che, fissato 1 quale primo numero esagonale, il secondo è: 1+5=6; il terzo è: 6+9=15; il quarto è: 15 +13 =28. Così procedendo, l’n-esimo numero esagonale sarà dato da: 1+5+9+...+(4n-3)=2n2 – n. Si possono ottenere gli stessi numeri utilizzando una formula ricorsiva: En+1 = En + 4n + 1, dove E0 = 0 Capitolo 18: Il numero aureo È noto che il numero Pi greco () espresso in forma decimale, e, arrestandosi alle prime due cifre, è 3,14; esso è, però, un numero la cui espansione decimale “non ha fine” e le cifre dell’espansione, finora note, si presentano a caso, senza alcuna ricorrenza o periodicità. Il numero , come si sa, rappresenta sia il rapporto tra l’area, A, di un cerchio e il quadrato del suo raggio, r, sia il rapporto tra la lunghezza, C, della circonferenza di un cerchio e il suo diametro, d, cioè: A 𝐂 =r r , = d La determinazione di tale numero, sin dall’età egizia, ha interessato i cultori della matematica. Con procedimenti pratici, gli egizi riuscirono a calcolare per tale numero un valore molto vicino a quello che noi oggi conosciamo. Infatti, nel Papiro di Rhind, si trova la più antica approssimazione di che, tradotta a notazione decimale, corrisponde a 3,16. Sia Euclide e sia, successivamente, Archimede sapevano che il rapporto tra l’area di un cerchio e il quadrato del diametro doveva essere un numero costante, indipendentemente dall’estensione del cerchio e dalla lunghezza del diametro. Archimede fornisce un valore numerico di questo rapporto, nel trattatello dal titolo Misura del Cerchio, alla proposizione 2: il cerchio ha rispetto al quadrato del diametro il rapporto che 11 ha rispetto a 14. Lo stesso Archimede dà, in particolare, un’approssimazione di 7 nella medesima opera alla proposizione 3: la circonferenza di ogni cerchio è tripla del diametro e lo supera ancora di meno di un settimo del diametro, e di più di dieci settantunesimi. Per trovare valori approssimati per difetto, Archimede sostituì al cerchio poligoni regolari inscritti in esso, mentre per trovare i valori approssimati per eccesso, ricorse allo studio dei poligoni regolari circoscritti. Considerando dapprima l’esagono regolare circoscritto al cerchio e poi quello inscritto allo stesso, Archimede raddoppiò successivamente il numero dei lati dei due poligoni, fino a giungere a poligoni regolari di 96 lati. Il trattatello Misura del Cerchio è una delle opere di Archimede più conosciute nel Medioevo. Questo piccolo trattato, molto probabilmente comprende soltanto tre proposizioni, la prima delle quali è la dimostrazione, mediante il “metodo di esaustione”, che: ogni cerchio è uguale ad un triangolo rettangolo se ha il raggio uguale ad un cateto e la circonferenza uguale alla base.