Definizione di circuito, delle grandezze circuitali e classificazione

Lezione 1 – Definizione di circuito, delle grandezze circuitali e classificazione dei bipoli
Lezione n.1
Definizione di circuito, delle grandezze circuitali e
classificazione dei bipoli
1.
Definizione di circuito elettrico
2.
Bipolo e relazione caratteristica di un bipolo
3.
Corrente elettrica
4.
Tensione elettrica e potenziale elettrico
5.
Potenza elettrica
6.
Classificazione dei bipoli
6.1 Bipoli controllati in tensione e controllati in corrente
6.2 Bipoli statici e bipoli dinamici
6.3 Bipoli passivi e bipoli attivi
6.4 Bipoli lineari
Tag:
circuito elettrico, bipolo, intensità di corrente (corrente), tensione, potenziale
elettrico, differenza di potenziale elettrico, relazione caratteristica, leggi di
Kirchhoff, terminali, morsetti, circuito elettrico, potenza elettrica assorbita e
generata, energia elettrica, Watt, Joule, bipoli passivi e attivi, bipoli statici e
dinamici, bipoli lineari e non lineari, bipoli controllati in tensione ed in corrente,
bipoli tempo invarianti e tempo varianti, convenzione del generatore e
dell’utilizzatore, curva caratteristica di un bipolo, principio di sovrapposizione degli
effetti
Corso di Elettrotecnica – Prof.ssa Lorenza Corti – A.A. 2012/13
1/10
Lezione 1 – Definizione di circuito, delle grandezze circuitali e classificazione dei bipoli
1. Definizione di circuito elettrico
Il circuito elettrico è un modello di un sistema fisico elettromagnetico.
In generale un sistema elettromagnetico è descritto dalle equazioni di Maxwell e dalle
relazioni costitutive dei mezzi presenti nel sistema. In particolari casi, sotto opportune
condizioni, il sistema si può descrivere in maniera semplificata utilizzando un
insieme di equazioni algebrico-differenziali che si derivano dalle equazioni di
Maxwell utilizzando opportune ipotesi. Tale approccio da luogo ad un modello del
sistema che chiamiamo circuito elettrico. Le equazioni che descrivono il sistema sono
quella della teoria dei circuiti.
Da un punto di vista fisico un circuito si presenta come una connessione di sistemi
detti componenti elettrici (o elettronici). Tali sistemi possono essere realizzati in
diversi modi, forme, dimensioni e composizione. Ogni sistema è collegato agli altri
attraverso almeno due conduttori supposti filiformi che chiamiamo terminali. Ogni
terminale sarà quindi collegato dal una parte al sistema e dall’altra avrà un morsetto
che viene utilizzato per collegarlo agli altri elementi.
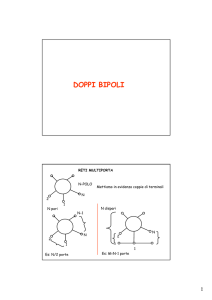
Nella parte introduttiva del corso esamineremo sistemi con solo due terminali, ma poi
vedremo che si possono considerare anche sistemi a più terminali come il
trasformatore o i doppi bipoli.
Le principali grandezze elettriche di interesse in un circuito sono le intensità delle
correnti elettriche nei terminali dei componenti e le tensioni elettriche che si
stabiliscono tra gli stessi. Tali grandezze sono variabili nel tempo.
In sintesi la possibilità di avere un approccio circuitale ad un sistema elettrico
dipende dalla possibilità di definire ai morsetti di ogni suo sistema costituente una
tensione elettrica e di assicurarsi che la somma delle correnti entranti (o uscenti) da
ogni sistema sia nulla.
Il funzionamento di un circuito dipende da due aspetti:
la natura di ogni sistema costituente il circuito e il modo in cui sono connessi tra loro
tutti i sistemi. Il primo aspetto ci serve a scrivere le relazioni caratteristiche dei
sistemi, mentre il secondo aspetto ci serve a scrivere le leggi di Kirchhoff. L’insieme
di tutte queste equazioni rappresenta il modello matematico che descrive il
funzionamento di ogni circuito.
2. Bipolo e relazione caratteristica di un bipolo
Il bipolo è un sistema elettrico dotato di due terminali terminati da due morsetti
attraversati da due correnti uguali (verso e valore), tra cui è possibile definire una
tensione. Il simbolo del bipolo è quello di Fig.1a.
Siccome sia la corrente i (t ) che la tensione v(t ) devono avere necessariamente un
verso, ogni bipolo avrà un verso per la corrente ed uno per la tensione. Quando i versi
applicati sono opposti (Fig. 1b), si dice che si è fatta la convenzione dell’utilizzatore;
viceversa, quando i segni sono concordi (Fig.1c), si dice che si è fatta la convenzione
del generatore.
Corso di Elettrotecnica – Prof.ssa Lorenza Corti – A.A. 2012/13
2/10
Lezione 1 – Definizione di circuito, delle grandezze circuitali e classificazione dei bipoli
Fig.1a – Simbolo del bipolo.
i(t)
i(t)
v(t)
Fig.1b – Convenzione dell’utilizzatore.
v(t)
Fig.1c – Convenzione del generatore.
Ogni bipolo è caratterizzato da un legame funzionale tra corrente e tensione.
Caratterizzare un bipolo significa assegnare la relazione funzionale tra i (t ) e v(t ).
Tale relazione funzionale prende il nome di relazione caratteristica e la indichiamo
nel modo seguente:
v(t )= r (i (t ), t ) oppure i (t ) = g (v (t ), t ) ,
∀t ∈ D .
(1)
dove D rappresenta un intervallo temporale di definizione delle relazioni funzionali
introdotte. Nel futuro sottintenderemo l’appartenenza della variabile temporale a
questo intervallo di definizione.
La variabile temporale compare nella funzione r ()
. o g ()
. in modo esplicito perché in
generale la relazione caratteristica può variare nel tempo. In questo caso parleremo di
bipoli tempo-varianti.
Nel caso contrario, il caso che noi utilizzeremo in tutto il corso, i bipoli si dicono
tempo-invarianti e le (1) diventano:
v(t ) = r (i(t )) oppure i (t ) = g (v(t )).
(2)
Le relazioni caratteristiche (2) (ma anche le (1)), e quindi le funzioni r(.) ed g(.)
hanno un segno che dipende dalla convenzione (generatore o utilizzatore) fatta sul
bipolo a cui si riferiscono. Vedremo infatti che quando introdurremo le caratteristiche
di ogni singolo tipo di bipolo (Lezione. 2) ciò che cambia nella relazione
caratteristica nel passare da una convenzione ad un'altra è un segno – davanti alla
funzione.
Corso di Elettrotecnica – Prof.ssa Lorenza Corti – A.A. 2012/13
3/10
Lezione 1 – Definizione di circuito, delle grandezze circuitali e classificazione dei bipoli
3. Intensità di corrente elettrica
La carica elettrica è una grandezza fondamentale in fisica. Si misura in Coulomb (C).
Le cariche elettriche in movimento costituiscono la intensità di corrente elettrica
i (t ), espressa dalla relazione
i (t ) =
dq(t )
,
dt
(3)
dove q(t ) rappresenta la quantità di carica netta che nel tempo t attraversa una
superficie aperta S come quella di Fig. 2.
La intensità di corrente verrà chiamata nel seguito semplicemente la corrente!
Nella definizione della corrente (3) è necessario indicare quale verso di attraversamento della
superficie S abbiamo considerato. Da questa scelta dipende il verso che attribuiamo alla corrente
che stiamo considerando. La corrente ha un verso. Non basta far riferimento ad una corrente se non
si specifica il suo verso di “attraversamento” del conduttore. Non c’è nessun motivo per preferire un
verso ad un altro: la scelta è del tutto arbitraria, basta specificarla sempre. Fissare un verso alla
corrente corrisponde a stabilire il segno del valore della corrente i (t ) in ogni istante che si
determinerà con quella scelta di verso fatta.
S
Fig.2 – Superficie attraversata da cariche elettriche.
Dalla (3), si definisce l’unità di misura della corrente, chiamata Ampère (A),
corrispondente a Coulomb su secondi.
La corrente è soggetta ad un principio di continuità: attraverso ogni superficie chiusa,
la somma delle correnti entranti (o uscenti) è nulla (nella somma si devono
considerare anche le correnti di spostamento di cui parleremo più avanti). Se, una
volta stabilita la superficie chiusa ed il suo verso di attraversamento (correnti entranti
o uscenti), avrò che alcune correnti potrebbero avere il loro verso discorde con quello
scelto per l’attraversamento della superficie dovrò considerare nella somma quella
corrente con il segno negativo.
Nei sistemi reali la corrente fluisce in conduttori che hanno sezione finita. Nella
teoria dei circuiti, dove non si tiene conto della dimensione fisica del sistema, si
suppone che i conduttori siano filiformi; si trascura cioè la sezione finita del
conduttore e si assume che la corrente di valore finito attraversi conduttori privi di
dimensione. Per indicare il verso della corrente che fluisce nei conduttori del nostro
Corso di Elettrotecnica – Prof.ssa Lorenza Corti – A.A. 2012/13
4/10
Lezione 1 – Definizione di circuito, delle grandezze circuitali e classificazione dei bipoli
circuito, usiamo una freccia come in Fig.3: se risulta che, per il verso scelto della
freccia il valore della corrente é positivo, allora vorrà dire che ho indicazione di
cariche positive che si muovono nel verso scelto. Comunque tale deduzione è
superflua ai fini della teoria dei circuiti, nella quale non siamo interessati a conoscere
il moto reale delle cariche.
i(t)
Fig.3 – Corrente in un conduttore filiforme.
4. Tensione elettrica e potenziale elettrico
La tensione v(t ) è una grandezza elettrica supposta esistente tra due punti dello
spazio. Nel nostro studio, questi due punti sono i due “morsetti” di un bipolo (definiti
nel prossimo paragrafo). Se il campo elettrico è irrotazionale in un dominio dello
spazio (questo accade ad esempio quando non c’è variazione di campo magnetico in
quel regione di spazio) possiamo dire che la tensione rappresenta il lavoro necessario
per spostare una carica unitaria da un punto all’altro di tale dominio. Indichiamo tali
punti con A e B, come in Fig.4.
In altre parole quando il campo elettrico è irrotazionale il lavoro compiuto per
spostare una carica unitaria da un punto A ad un punto B è indipendente dal percorso
scelto tra i due punti. In questo caso possiamo introdurre una funzione scalare φ detta
potenziale elettrico definita in ogni punto del dominio in cui si trovano A e B e
possiamo definire la tensione tra A e B come una differenza di potenziale (d.d.p.)
secondo la relazione
v AB (t ) = φ A (t )− φ B (t ),
(4)
dove φ è il potenziale elettrico nel punto indicato con il pedice corrispondente. La
tensione, e quindi il potenziale elettrico, si misura in Volt (V). Graficamente la
tensione esistente tra due punti nello spazio si indica con una freccia come in Fig. 4.
Poiché la tensione è definita utilizzando il lavoro di uno spostamento di carica da un
punto ad un altro, è necessario introdurre per essa un “verso”. Questo corrisponderà
al verso della freccia. La tensione v AB con il verso come rappresentato in Fig.4, è
quella relativa allo spostamento di una carica unitaria dal punto A al punto B. Il
potenziale in A è maggiore di quello in B se v AB > 0 .
Corso di Elettrotecnica – Prof.ssa Lorenza Corti – A.A. 2012/13
5/10
Lezione 1 – Definizione di circuito, delle grandezze circuitali e classificazione dei bipoli
B
vAB
A
Fig. 4 – Verso della tensione in relazione allo spostamento della carica unitaria.
5. Potenza elettrica
Cominciamo con l’introdurre l’energia elettrica assorbita, che chiamiamo w(t ) , da
un bipolo nell’intervallo di tempo (0;t); tale grandezza è misurata in Joule (J). Se
w(t ) nell’intervallo di tempo (0;t) è effettivamente assorbita dal bipolo risulta di
segno positivo in caso contrario di segno negativo e potremmo dire che il bipolo ha
ceduto energia verso l’esterno nell’intervallo di tempo (0;t).
La potenza elettrica assorbita p (t ) corrisponde alla variazione d’energia elettrica
assorbita nell’unità di tempo da un bipolo ed è data dalla relazione
p (t ) =
dw(t )
dt
(5)
ed è misurata in Watt (W) che equivale a Joule su secondi.
La potenza assorbita descrive in che modo l’energia che il bipolo stà assorbendo varia
nel tempo. Se la potenza assorbita è positiva vorrà dire che assistiamo ad un aumento
dell’energia immagazzinata dal bipolo (energia elettrostatica o magnetica). Se la
potenza assorbita è negativa vorrà dire che l’energia immagazzinata del componente
stà diminuendo perché stà fluendo verso l’esterno del sistema mettendola a
disposizione degli altri componenti o dell’ambiente.
Quando la potenza (assorbita o erogata) è nulla vuol dire che non c’è variazione di
energia e che il bipolo non scambia energia con l’esterno ed eventualmente
immagazzina una energia costante (elettrostatica o magnetica).
Si può dimostrare che in un bipolo si ha:
p (t ) = v(t )i (t ) .
Corso di Elettrotecnica – Prof.ssa Lorenza Corti – A.A. 2012/13
(6)
6/10
Lezione 1 – Definizione di circuito, delle grandezze circuitali e classificazione dei bipoli
e che, qualora sia stata fatta la convenzione dell’utilizzatore sul bipolo, la potenza
definita dalla (6) è una potenza assorbita; viceversa, qualora si usi la convenzione del
generatore, la potenza che calcolo è quella generata o erogata dal bipolo.
6. Classificazione dei bipoli
In questo paragrafo ci occuperemo di fare una classificazione dei bipoli. A tale scopo
introdurremo alcune proprietà che caratterizzano ogni bipolo e che lo fanno
appartenere ad una classe piuttosto che un'altra.
6.1 Bipoli tempo-varianti e tempo-invarianti
Definiamo bipoli tempo-varianti quelli per cui vale la caratteristica:
v(t )= r (i (t ), t ) oppure i (t ) = g (v (t ), t ) .
(7)
Nel caso contrario, il caso che noi utilizzeremo in tutto il corso, i bipoli si dicono
tempo-invarianti e le (7) diventano:
v(t ) = r (i(t )) oppure i (t ) = g (v(t )).
(8)
In altre parole il bipolo si dice tempo invariante quando le sue caratteristiche elettromagnetiche non variano nel tempo. La tempo invarianza è sempre riferita a
l’intervallo di tempo in cui studiamo quel particolare sistema. Un resistore, un
condensatore e un induttore tempo invarianti sono caratterizzati dall’avere, nel range
temporale in cui li utilizziamo, rispettivamente la resistenza, la conduttanza e
l’induttanza costanti rispetto al tempo.
6.2 Bipoli controllati in tensione e bipoli controllati in corrente
Definiamo bipoli controllati in tensione i bipoli per i quali possiamo scrivere la
relazione caratteristica con la tensione variabile indipendente:
i (t ) = g (v(t )).
(9)
Viceversa: definiamo bipoli controllati in corrente i bipoli per i quali possiamo
scrivere:
v(t ) = r (i(t )).
Corso di Elettrotecnica – Prof.ssa Lorenza Corti – A.A. 2012/13
(10)
7/10
Lezione 1 – Definizione di circuito, delle grandezze circuitali e classificazione dei bipoli
Nel primo caso possiamo dire che per ogni valore della tensione esiste un solo valore
della corrente. Viceversa, nel secondo caso.
Non è detto che le funzioni g ()
. ed r (.) siano invertibili. Nel caso in cui questo
accadesse potremmo scrivere:
g (.) = r .1 (.) .
(11)
Esistono bipoli per i quali la (11) è verificata e che quindi sono controllati sia in
tensione che in corrente, ad esempio, come vedremo nella prossima lezione, i resistori
lineari.
6.3 Bipoli statici e bipoli dinamici
Si definisce bipolo statico un bipolo nel quale la tensione (la corrente) in un istante
. (o
dipende dalla corrente (dalla tensione) nello stesso istante. In questo caso la r ()
g ()
. ) della (2) è una funzione in cui non compaiono derivate. Per i bipoli statici è
sempre possibile considerare una curva caratteristica. Questa è la curva nel piano i v relativa alla funzione r ()
. (o g ()
. ). In Fig. 5 abbiamo rappresentato un esempio di
resistore non lineare.
Sono bipoli statici il resistore i generatori ideali, gli interruttori.
v
i
Fig. 5 – Grafico della funzione caratteristica di un resistore (in questo caso non
lineare).
Si definisce bipolo dinamico un bipolo nel quale la tensione (la corrente) in un istante
dipende dalla corrente (dalla tensione) nello stesso istante e negli istanti precedenti (o
almeno da parte di questi) ad esso, cioè dipende dalla storia passata.
In questo caso la r ()
. (o g ()
. ) della (2) è una funzione in cui compaiono derivate.
In questo caso non possiamo utilizzare una curva caratteristica.
Corso di Elettrotecnica – Prof.ssa Lorenza Corti – A.A. 2012/13
8/10
Lezione 1 – Definizione di circuito, delle grandezze circuitali e classificazione dei bipoli
Sono bipoli dinamici il condensatore e l’induttore.
6.4 Bipoli passivi e bipoli attivi
Un bipolo statico è passivo se la potenza assorbita (generata) è positiva (negativa).
Viceversa, è attivo se la potenza assorbita (generata) è negativa (positiva).
Se il bipolo è attivo, vuol dire che al suo interno le cariche si muovono in senso
opposto al campo elettrico che determina quella tensione (cioè non vanno più da un
punto a potenziale maggiore ad uno a potenziale minore), pertanto si dovrà
ammettere l’esistenza di forze di altra natura (chimica, meccanica, ...) che “forzano”
le cariche a muoversi in opposizione al campo elettrico esistente. E’ il caso questo del
bipoli generatori che introdurremo nella prossima lezione.
Il resistore è un bipolo passivo.
Per i bipoli dinamici che introdurremo nella prossima lezione, cioè l’induttore e il
condensatore, non è possibile utilizzare la definizione appena data di bipolo passivo e
attivo. In questo caso, infatti, il segno della potenza assorbita (o erogata) definita
come prodotto v(t )(
i t ) non è definibile a priori. Questo dipenderà dallo “stato” in cui
si trova il bipolo dinamico.
In questo caso, allora, si ricorre ad una diversa definizione. Si definisce passivo un
bipolo per il quale si ha
t
∫ p(t )dt =w(t ) − w(− ∞ ) ≥ 0 .
(9)
−∞
Osserviamo che il secondo membro della (9) rappresenta l’energia assorbita dal
bipolo fino all’istante t. Deve accadere che l’energia immagazzinata dall’origine dei
tempi è non negativa. Questo vuol dire che tali bipoli non possono erogare un’energia
che non gli ha fornito precedentemente un generatore. Il condensatore e l’induttore
sono bipoli dinamici passivi. Essi possono essere caricati da un generatore,
immagazzinare energia ed eventualmente scaricarsi fornendo energia all’esterno.
Questi bipoli dunque possono fungere temporaneamente da generatori ma solo di
un’energia che gli è stata precedentemente fornita da generatori.
6.5 Bipoli lineari
Un bipolo si dice lineare se ad una combinazione lineare di tensioni (correnti)
esistenti nel bipolo corrisponde la stessa combinazione lineare delle correnti
(tensioni) del bipolo. Si ha quindi che per un bipolo controllato in corrente
Corso di Elettrotecnica – Prof.ssa Lorenza Corti – A.A. 2012/13
9/10
Lezione 1 – Definizione di circuito, delle grandezze circuitali e classificazione dei bipoli
v(t ) = r (a1i1 (t ) + a2i2 (t ) ) = a1r (i1 (t ) ) + a2 r (i2 (t ) ) = a1v1 (t ) + a2 v2 (t ) .
(10)
Noi in questo corso utilizzeremo solo bipoli passivi lineari. I bipoli attivi che
considereremo, come vedremo tra breve, non sono bipoli lineari.
Un circuito avente elementi passivi lineari lo definiamo circuito lineare.
In questo caso vale il principio di sovrapposizione degli effetti. Questo afferma che
se in un circuito vi sono più generatori, le tensioni e le correnti del circuito sono la
sovrapposizione delle grandezze corrispondenti ad ogni singolo generatore.
Corso di Elettrotecnica – Prof.ssa Lorenza Corti – A.A. 2012/13
10/10