Valori estremi e rischi assicurativi
Tratto da Sis-Magazine
http://old.sis-statistica.org/magazine
Valori estremi e rischi
assicurativi
- Articoli -
Data di pubblicazione : giovedì 3 novembre 2011
Sis-Magazine
Copyright © Sis-Magazine
Page 1/6
Valori estremi e rischi assicurativi
Tradizionalmente rivolta ad ambiti propri dellingegneria e delle scienze ambientali (climatologia, idrologia, geologia),
la teoria statistica dei valori estremi ha recentemente conquistato un ruolo di primo piano nelle discipline attuariali e
finanziarie. Alcune fondamentali pubblicazioni apparse negli Anni Novanta (ad esempio Beirlant, Teugels e Vynckier,
1996; Embrechts, Klüppelberg e Mikosch, 1997) hanno, infatti, accreditato la convinzione che una metodologia
appropriata per modellare perdite estreme in contesti assicurativi e finanziari sia la stessa che da tempo viene
applicata per valutare leccezionalità degli eventi di pioggia intensa (cfr. La statistica ed il dissesto idrogeologico di
A. Bodini su SIS-Magazine del 19.04.2010) o i livelli massimi delle maree in zone soggette a rischio di inondazioni
(cfr. Valori estremi e analisi dei rischi ambientali di S. A. Padoan su SIS-Magazine del 13.05.2011). Un contesto
privilegiato per illustrare questo parallelismo riguarda la valutazione dei trattati di riassicurazione.
Nonostante la maggioranza delle persone sia titolare di una o più polizze assicurative, nessun soggetto privato entra
normalmente in contatto con il ramo della riassicurazione. Questultimo ha dunque vissuto nellanonimato per circa
150 anni, considerato che la fondazione della prima riassicurazione professionale, Cologne Re, è avvenuta nel 1842
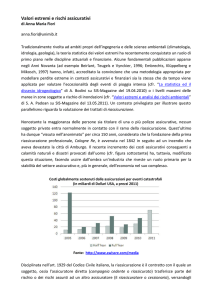
in seguito ad un incendio che aveva devastato la città di Amburgo. Il recente incremento dei costi assicurativi
conseguenti a calamità naturali e disastri provocati dalluomo (cfr. figura sottostante) ha, tuttavia, modificato questa
situazione, facendo uscire dallombra unindustria che riveste un ruolo primario per la stabilità del settore assicurativo
e, più in generale, delleconomia nel suo complesso.
Disciplinata nellart. 1929 del Codice Civile italiano, la riassicurazione è il contratto con il quale un soggetto, ossia
lassicuratore diretto ( compagnia cedente o riassicurato) trasferisce parte del rischio o dei rischi assunti ad un altro
assicuratore (il riassicuratore o cessionario), versandogli contestualmente un premio. A questo contratto rimane
estraneo lassicurato principale, che non ha rapporti diretti con il riassicuratore. Sotto il profilo tecnico-economico, i
vantaggi per la compagnia cedente spaziano da una composizione più equilibrata del portafoglio di rischi
allampliamento della capacità di sottoscrizione, alla riduzione del capitale proprio a copertura dellattività (come
consentito nellattuale regime di Solvency I[Disciplina di vigilanza prudenziale del settore assicurativo europeo, che
prescrive dei capitali minimi a garanzia degli impegni assunti nei confronti degli assicurati.]). Sul piano
economico-sociale, la riassicurazione consente di rendere assicurabili rischi che per la loro natura, per le dimensioni
o per lesposizione a particolari situazioni di casualità (concentrazione di rischi, ad esempio lincendio di un
grattacielo, ed il conseguente cumulo di sinistri) non sarebbero normalmente assumibili. I principali attori del mercato
riassicurativo sono necessariamente società di dimensioni rilevanti, che diversificano i rischi su base mondiale,
Copyright © Sis-Magazine
Page 2/6
Valori estremi e rischi assicurativi
avvalendosi frequentemente della retrocessione ad altre compagnie riassicurative. Munich Re, Swiss Re, Hannover
Re, Berkshire Hathaway e Lloyds sono le prime cinque presenti sul mercato, ordinate in base alla raccolta premi nel
2009.
Nella pratica, i trattati riassicurativi si distinguono in proporzionali e non proporzionali. La riassicurazione
proporzionale, che prevede una suddivisione pro-quota di responsabilità e premi tra assicuratore diretto e
riassicuratore, è comunemente utilizzata per rischi di moderata entità. A fronte di eventi rari ma potenzialmente in
grado di compromettere la solvibilità delle compagnie cedenti (ad es. un terremoto, un incendio distruttivo&), lofferta
delle società di riassicurazione si è progressivamente orientata verso soluzioni alternative, sviluppando apposite
coperture di tipo non proporzionale.
Nella riassicurazione non proporzionale per eccesso di sinistro (excess of loss, o XL), lobbligo di prestazione del
riassicuratore scatta soltanto quando il danno supera un limite monetario D (priorità) contrattualmente prefissato,
cosicché restano in carico allassicuratore diretto tutti i risarcimenti di entità non superiore a D. Nella terminologia
propria del ramo vita, il limite D è chiamato livello di ritenzione della compagnia cedente, mentre nel ramo danni in
cui lentità del danno da risarcire non è nota in anticipo si usa di preferenza il termine deducibile. Se si denota con Y
la variabile casuale rappresentativa del danno oggetto di copertura riassicurativa, limpegno a carico del
riassicuratore in un trattato XL con priorità D si concretizza nel risarcimento dellimporto (aleatorio):
[http://latex.codecogs.com/gif.latex?%28Y-D%29_+%20%3D%20%5Cbegin%7Bcases%7D%200%20%26%20
%5Ctext%7Bse%20%7D%20Y%20%5Cleq%20D%20%5C%5C%20Y-D%20%26%20%5Ctext%7Bse%20%7D%20Y
%20%3E%20D.%20%5Cend%7Bcases%7D]
Il premio equo[http://latex.codecogs.com/gif.latex?%5CPi_Y(D)] per questo impegno risarcitorio corrisponde al suo
valore atteso (aspettativa o media), al quale concorre il contributo di due fattori:
[http://latex.codecogs.com/gif.latex?%5CPi_Y(D)%20=%20%5Ctext%7BValore%20Atteso%7D%5Cleft%5B%20(Y-D
)_+%20%5Cright%20%5D%20=%20%5Cmathbf%7Be_Y(D)%20%5Ctimes%20%5Cbar%7BF%7D_Y(D)%7D%20%
5Cqquad%5Cqquad%20(1)]
Il termine[http://latex.codecogs.com/gif.latex?\mathbf{\bar{F}_Y(D)}] - funzione di sopravvivenza di Y calcolata in D rappresenta la probabilità di osservare un danno eccedente la priorità D contrattualmente prefissata: Prob (Y > D). Il
termine[http://latex.codecogs.com/gif.latex?\mathbf{e_Y(D)}] funzione eccesso medio esprime invece,
condizionatamente al verificarsi dellevento (Y > D), il valore atteso del corrispondente eccesso di danno Y-D. Pur
non richiedendo la conoscenza dellintera distribuzione di probabilità di Y, la (1) presenta unintrinseca difficoltà di
valutazione in conseguenza della rarità di eventi significativi per il calcolo sia di
[http://latex.codecogs.com/gif.latex?\mathbf{\bar{F}_Y(D)}] sia di[http://latex.codecogs.com/gif.latex?\mathbf{e_Y(D)}]
.
Questa considerazione viene di seguito esemplificata su un dataset assicurativo incluso nei moduli software EVIR ed
EVIM, che eseguono analisi statistiche di valori estremi in ambienti, rispettivamente, R e Matlab. Il dataset dan
comprende danni da incendio di entità almeno pari ad 1 milione di Corone danesi (DKK), verificatisi fra il 1980 ed il
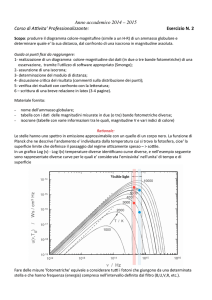
1990 e rivalutati ai prezzi del 1985 per tenere conto dellinflazione del periodo (Fonte: Danish Re). Gli n = 2167 valori
del dataset (figura sottostante) possono intendersi come altrettante realizzazioni campionarie y1,&,yn del danno
globale Y (ad edifici, arredi, oggetti personali& incluse eventuali perdite di profitto) in conseguenza dellincendio. In
figura è visualizzata unipotetica ripartizione del danno fra assicuratore diretto e riassicuratore in presenza di
copertura riassicurativa XL con priorità D = 150 milioni di DKK.
ü
Copyright © Sis-Magazine
Page 3/6
Valori estremi e rischi assicurativi
Poiché il campione a disposizione include due sole eccedenze rispetto a 150 (rispettivamente 263,25 e 152,41,
visualizzate in figura), una stima intuitiva della funzione[http://latex.codecogs.com/gif.latex?\mathbf{e_Y(D)}] si
ottiene prendendo la media aritmetica dei due corrispondenti eccessi di danno: ü
[http://latex.codecogs.com/gif.latex?%5Cfrac%7B(263.25%20-%20150)%20+%20(152.41-150)%7D%7B2%7D%20=
%2057.83]
mentre[http://latex.codecogs.com/gif.latex?\mathbf{\bar{F}_Y(D)}] - ovvero la probabilità dellevento (Y > 150) può
essere approssimata con la sua frequenza relativa campionaria:
[http://latex.codecogs.com/gif.latex?fr(Y%3E150)%20=%20%5Cfrac%7B2%7D%7B2167%7D%20=%200.00092]
Inseriti nella (1), questi risultati consentono unimmediata valutazione empirica del premio equo di riassicurazione
(in milioni di DKK):
[http://latex.codecogs.com/gif.latex?%5Chat%5CPi_%7BEMP%7D(D)%20=%20%5Cunderset%7B57.83%7D%7B%
5Cunderbrace%7B%5Cmathbf%7Be_%7BMP%7D(D))%7D%7D%7D%20%5Ccdot%20%5Cunderset%7B0.00092%
7D%7B%5Cunderbrace%7B%5Cmathbf%7BF_%7BEMP%7D(D))%7D%7D%7D%20=%200.0534]
Chiaramente, laffidabilità di un calcolo basato su due sole osservazioni campionarie non può che suscitare qualche
perplessità. Peggio ancora: che cosa succederebbe se la compagnia cedente volesse fissare D ad un livello
superiore a 263.25 (ovvero il massimo danno storicamente accertato)? Semplicemente, la serie storica a
disposizione non conterrebbe linformazione necessaria per una valutazione puramente empirica del premio di
riassicurazione (1).
Una soluzione alternativa per quantificare il premio di questa copertura riassicurativa proviene dall'analisi statistica
dei valori estremi, la cui variante condizionale propone di descrivere la distribuzione delle ultime osservazioni,
ovvero quelle superiori ad unopportuna soglia u (threshold), tramite un modello parametrico fornito dalla legge di
Pareto generalizzata (GP). Condizionatamente al verificarsi di un sinistro Y eccedente u, la probabilità che l'eccesso
di danno (Y u) superi un determinato valore y può essere approssimata mediante la funzione di sopravvivenza:
[http://latex.codecogs.com/gif.latex?%5Cbar%7BG%7D_%7B%5Cxi,%5Cbeta%7D(y)%20=%20%5Cbegin%7Bcases
%7D%20%5Cleft(%201%20+%20%5Cxi%20%5Cfrac%7By%7D%7B%5Cbeta%7D%20%5Cright%20)%5E%7B-%5
Cfrac1%5Cxi%7D%20&%20%5Cxi%20%5Cneq%200%20%5C%5C%20e%5E%7B-%5Cfrac%7By%7D%7B%5Cbet
a%7D%7D%20&%20%5Cxi%20=0%20%5Cend%7Bcases%7D]
dipendente dai due parametri[http://latex.codecogs.com/gif.latex?\xi] (forma) e[src] 0"> (scala). Stimati questi ultimi
con opportuni metodi statistici, lapprossimazione GP consente una valutazione parametrica del premio equo (1)
Copyright © Sis-Magazine
Page 4/6
Valori estremi e rischi assicurativi
muovendo da un approccio noto come "Peaks-over-Threshold" (POT), per la cui descrizione si rimanda ai testi
segnalati in bibliografia. Le condizioni di validità per questa approssimazione sono analoghe a quelle richieste nella
versione classica della teoria dei valori estremi per lutilizzo di una legge GEV di identico parametro
[http://latex.codecogs.com/gif.latex?\xi] - come distribuzione limite per i massimi campionari (cfr. Padoan,
SIS-Magazine, 2011). Si tratta di condizioni tipicamente soddisfatte dalla maggioranza delle distribuzioni di uso
comune in statistica (dallesponenziale alla gamma, dalla normale alla lognormale, dalla Dagum alla Weibull...).
Data la priorità D = 150, il metodo POT fornisce una stima parametrica del premio equo (1) pari a:
[http://latex.codecogs.com/gif.latex?%5Chat%5CPi_%7BPOT%7D(D)%20=%20%5Cunderset%7B152.37%7D%7B%
5Cunderbrace%7B%5Cmathbf%7Be_%7BPOT%7D(D)%7D%7D%7D%20%5Ccdot%20%5Cunderset%7B0.000405
%7D%7B%5Cunderbrace%7B%5Cmathbf%7B%5Cbar%7BF%7D_%7BPOT%7D(D)%7D%7D%7D%20=%200.061
7]
un risultato sensibilmente superiore alla precedente valutazione empirica (0,0534). Il confronto fra le due
impostazioni, lempirica e la parametrica, è stato replicato al variare del deducibile D, riscontrando le divergenze
riportate in tabella:
Mentre un approccio puramente empirico diventa meno consigliabile al diminuire del numero di eccedenze
campionarie osservate (e del tutto impraticabile per D > 263,25 = max(y1,&,yn)), il metodo POT basato sulla teoria
dei valori estremi consente una valutazione parametrica della (1) anche in corrispondenza di D prossimo -o
addirittura esterno- al range campionario.
Specificamente rivolta alla modellizzazione di eventi rari, lanalisi statistica dei valori estremi può fornire un utile
supporto quantitativo nella determinazione dei premi di riassicurazione e, più in generale, nella valutazione
probabilistica dei costi associati a rischi estremi o catastrofali. Tuttavia, non potendo per definizione operare su
numerosità campionarie elevate, questa metodologia è soggetta ad ampi margini di incertezza. Analisi di scenario,
rivalutazione dei risultati al variare della soglia prescelta per lapprossimazione GP, prove di stress vanno
necessariamente affiancate alla tecnica di base al fine di consentirne unapplicazione consapevole e calibrata ai casi
concreti.
Per saperne di più
Copyright © Sis-Magazine
Page 5/6
Valori estremi e rischi assicurativi
& Sulla riassicurazione:
Swiss Re, The essential guide to reinsurance. http://www.swissre.com/publications/
Romanello, L., Stocco, A. (2011). Assicurazioni vita: rischio, solvibilità e riassicurazione. Seminario presentato al
Dipartimento di Metodi Quantitativi per le Scienze Economiche ed Aziendali, Università di Milano-Bicocca. Testo
della presentazione accessibile da: http://web-nuovo.dimequant.unimib.i...
& Sullanalisi statistica dei valori estremi e le sue applicazioni finanziarie/assicurative:
Beirlant, J., Teugels, J.L., Vynckier, P. (1996). Practical analysis of extreme values. Leuven University Press.
Embrechts, P., Klüppelberg, C., Mikosch, T. (1997). Modelling extremal events for insurance and finance.
Springer, Berlin.
Beltrami, D. (2010). Lanalisi statistica dei valori estremi: aspetti metodologici ed applicazioni finanziarie. Tesi di
laurea magistrale in Economia e Finanza, Università di Milano-Bicocca.
Zerbinati, F. (2011). La riassicurazione e lanalisi statistica dei valori estremi. Tesi di laurea magistrale in
Economia e Finanza, Università di Milano-Bicocca.
Lautore
Anna Maria Fiori, Dipartimento di Metodi Quantitativi per le Scienze Economiche ed Aziendali, Università di
Milano-Bicocca (anna.fiori_AT_unimib.it)
Copyright © Sis-Magazine
Page 6/6