Esercitazioni di Teoria dei Sistemi

Davide Giglio
Esercitazioni di Teoria dei Sistemi
Anno Accademico 2010/2011
Esercitazione del 23 marzo 2011
DIAGRAMMI A BLOCCHI
TRASFORMATE ZETA
Esercitazione del 23 marzo 2011
Diagrammi a blocchi – Trasformate zeta
15.1
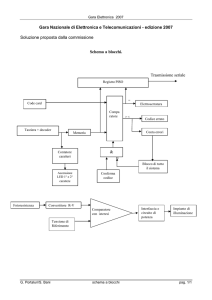
Si consideri il sistema rappresentato dal seguente diagramma a blocchi
d(t)
+
u(t)
−
1
(s + 1)(s + 10)
+
y(t)
+
k
dove d(t) = 2 sin 4t rappresenta un generico disturbo.
Si determini k in modo da avere un’attenuazione del disturbo d(t) pari a 10 volte.
Davide Giglio – Esercitazioni di Teoria dei Sistemi – Anno Accademico 2010/2011
2
Esercitazione del 23 marzo 2011
Diagrammi a blocchi – Trasformate zeta
15.2
Si consideri il sistema rappresentato dal seguente diagramma a blocchi
+
+
1
(s + 1)(s + 3)
u(t)
+
y(t)
+
k
s
h
s
1. Studiare la controllabilità e l’osservabilità, al variare di k != 0 e h != 0, sia attraverso l’algebra
dei blocchi sia mettendo il sistema in equazioni di stato.
√
√
2. Per k = 3 e h = 3, determinare
la parte oscillante di y(t) in corrispondenza di condizioni
√
iniziali nulle e u(t) = sin 3t.
Eliminiamo innanzitutto, attraverso l’algebra dei blocchi, i due nodi sommatori.
+ ! !
!
+
"
!
+ ! !
!
+
"
!
k
s
↓
↓
!
h
s
s+k
s
!
!
s+h
s
!
Il sistema può essere riscritto nel seguente modo
u(t)
!
!
s+k
s
1
(s + 1)(s + 3)
!
s+h
s
!
y(t)
Per studiare la controllabilità e l’osservabilità attraverso l’algebra dei blocchi, devo andare a vedere le possibili
cancellazioni polo/zero e zero/polo. E’ noto infatti che una qualsiasi cancellazione polo/zero implica la non
completa osservabilità del sistema e una qualsiasi cancellazione zero/polo implica la non completa controllabilità
del sistema.
Quindi:
• Il sistema risulta non completamente controllabile e completamente osservabile se
k=1
∪
k=3
∪
h != 1
∪
h != 3
• Il sistema risulta completamente controllabile e non completamente osservabile se
k != 1
∪
k != 3
∪
h=1
∪
h=3
• Il sistema risulta non completamente controllabile e non completamente osservabile se
k=1
∪
k=3
∪
h=1
∪
h=3
• Il sistema risulta completamente controllabile e completamente osservabile se
k != 1
∪
k != 3
∪
h != 1
∪
h != 3
Davide Giglio – Esercitazioni di Teoria dei Sistemi – Anno Accademico 2010/2011
13
Esercitazione del 23 marzo 2011
Diagrammi a blocchi – Trasformate zeta
Metto il sistema in equazioni di stato
u(t)
!
S1
!
S2
!
S3
!
y(t)
Le relazioni ingresso/uscita dei sottosistemi sono
S1 : ẏ1 (t) = u̇1 (t) + ku1 (t)
S2 : ÿ2 (t) + 4ẏ2 (t) + 3y2 (t) = u2 (t)
S3 : ẏ3 (t) = u̇3 (t) + hu3 (t)
Utilizzando, per ciascuno dei tre sottosistemi, la forma compagna controllabile, si ottiene
!
ẋ1 (t) = u1 (t)
S1 :
y1 (t) = kx1 (t) + u1 (t)

%
&
% &
0
1
0

ẋ2 (t) =
x2 (t) +
u (t)
−3
−4
1 2
S2 :
'
(

y2 (t) = 1 0 x2 (t)
!
ẋ3 (t) = u3 (t)
S3 :
y3 (t) = hx3 (t) + u3 (t)
Le relazioni tra gli ingressi e le uscite dei sottosistemi sono
u1 (t) = u(t)
u2 (t) = y1 (t)
u3 (t) = y2 (t)
y(t) = y3 (t)
Si ha quindi
ẋ1 (t) = u(t)
ẋ2,1 (t) = x2,2 (t)
ẋ2,2 (t) = −3x2,1 (t) − 4x2,2 (t) + kx1 (t) + u(t)
ẋ3 (t) = x2,1 (t)
y(t) = hx3 (t) + x2,1 (t)
e il sistema in equazioni di stato è



 
0 0
0 0
1



0 0
0

1 0




x(t) +  
u(t)
ẋ(t) = 
k −3 −4 0
1


0( 0
0


'0 1

y(t) = 0 1 0 h x(t)
'
Determino la controllabilità e l’osservabilità attraverso lo studio del rango delle matrici P ! B | AB | A2 B |


C


(
CA

A3 B e Q ! 
 CA2 .
CA3

0
0
2
A =
k
0
0
0
−3
1
0
1
−4
0

0
0
0
0

0 k
0
0
 
0
0
0 0
 k
0
1 0
=
−3 −4 0 −4k
0
1
0 0

0
0 0
−3 −4 0

12 13 0
0
1 0
Davide Giglio – Esercitazioni di Teoria dei Sistemi – Anno Accademico 2010/2011
14
Esercitazione del 23 marzo 2011

0

0
A3 = 
k
0
0
0
−3
1
0
1
−4
0

0
0
 k
0

0 −4k
0
0
Diagrammi a blocchi – Trasformate zeta
 
0
0 0
0
−4k
−3 −4 0
=
12 13 0  13k
0
1 0
k

0
0
0
12
13 0

−39 −40 0
−3 −4 0
Si ha


1
0
0
0
0
1
k−4
13 − 4k 

P =
1 k − 4 13 − 4k 13k − 40
0
0
1
k−4
'
(
det P = (13 − 4k)(k − 4) − (13k − 40) +
'
(
− (k − 4) (k − 4)2 − (13 − 4k) =
= 13k − 52 − 4k 2 + 16k − 13k + 40+
− (k − 4)[k 2 + 16 − 8k − 13 + 4k] =
= 13k − 52 − 4k 2 + 16k − 13k + 40+
− k 3 + 4k 2 − 3k + 42 − 16k + 12 =
= −k 3 + 4k 2 − 3k =
= −k(k 2 − 4k + 3) =
= −k(k − 3)(k − 1)
Il rango della matrice P è massimo quando k != 0, k != 1 e k != 3. Di conseguenza, essendo per ipotesi k != 0, il
sistema risulta non completamente controllabile per
k=1
∪
k=3
La matrice Q è

0
 0
Q=
 k
kh − 4k

1
0
h
h
1
0

−3
h−4
0
12 − 3h 13 − 4h 0
0'
(
k(12 − 3h) + 3(kh − 4k) +
'
(1
− h k(13 − 4h) − (kh − 4k)(h − 4) =
2
= h [12k − 3kh + 3kh − 12k]+
det Q = h
3
− h[13k − 4kh − kh2 + 4kh + 4kh − 16k] =
= −3kh + 4kh2 − kh3
Suppongo, come da ipotesi, h != 0 e k != 0 e considero
h3 − 4h2 + 3h = h(h2 − 4h + 3) =
= h(h − 1)(h − 3)
Il rango della matrice Q è massimo quando h != 1 e h != 3. Di conseguenza, il sistema risulta non completamente
osservabile per
h=1
∪
h=3
Pongo
h=k=
√
3
Davide Giglio – Esercitazioni di Teoria dei Sistemi – Anno Accademico 2010/2011
15
Esercitazione del 23 marzo 2011
Diagrammi a blocchi – Trasformate zeta
La funzione di trasferimento del sistema può essere agevolmente calcolata dal sistema iniziale utilizzando
l’algebra dei blocchi.
√
√
√
1
s+ 3
(s + 3)2
s+ 3
T (s) =
·
·
= 2
s
(s + 1)(s + 3)
s
s (s + 1)(s + 3)
L’ingresso dato, nella variabile complessa s, è
√
0
√ 1
3
U (s) = L sin 3t = 2
s +3
Essendo nulle le condizioni iniziali, l’uscita del sistema è data da
Y (s) = T (s) · U (s)
La parte oscillante di y(t) si può determinare utilizzando la teoria sulla risposta in frequenza. Il modulo della
parte oscillante è dato da
4 √ 4
4T ( 3j)4
mentre la fase da
' √ (
Φ T ( 3j)
Si ha quindi
√
√
4
4
4
4 √ 4 4
(
3j + 3)2
4
4T ( 3j)4 = 4
√
√
4 −3( 3j + 1)( 3j + 3) 4 =
4
4
4
4
−3 + 3 + 6j
4=
√
√
= 44
−3(−3 + 3 3j + 3j + 3) 4
4
4
4 6j 4
4
√ 4=
=4
−12 3j 4
1
= √
2 3
%
&
' √ (
1
Φ T ( 3j) = Φ − √ + 0j =
2 3
= π + arctan 0 =
=π
La parte oscillante di y(t) è
√
√
1
1
yo (t) = √ sin ( 3t + π) = − √ sin 3t
2 3
2 3
Davide Giglio – Esercitazioni di Teoria dei Sistemi – Anno Accademico 2010/2011
16
Esercitazione del 23 marzo 2011
Diagrammi a blocchi – Trasformate zeta
15.3
Determinare la trasformata zeta del segnale in figura
y(k)
•
2
1
0.5
•
•
0
1
•
2
•
3
4
•
5
•
k
6
Il segnale in figura può essere scritto analiticamente come
y(k) = δ(k − 1) + δ(k − 2) +
1
δ(k − 3) + 2 δ(k − 4)
2
Essendo
2
3
Z δ(k − n) = z −n
(trasformata zeta di un impulso traslato nel tempo), si ha
2
3
1
1
1
2
1
Y (z) = Z y(k) = z −1 + z −2 + z −3 + 2 z −4 = + 2 + 3 + 4 =
2
z z
2z
z
2z 3 + 2z 2 + z + 4
=
2z 4
Davide Giglio – Esercitazioni di Teoria dei Sistemi – Anno Accademico 2010/2011
19
Esercitazione del 23 marzo 2011
Diagrammi a blocchi – Trasformate zeta
15.4
Determinare la trasformata zeta del segnale in figura
u(k)
•
5
•
4
•
3
•
2
•
•
•
1
•
0
1
k
2
3
4
5
6
7
Il segnale in figura può essere scritto analiticamente come
'
(
'
(
u(k) = k · 1(k) − 1(k − 2) + 2 · 1(k − 2) − 1(k − 4) + (k − 2) · 1(k − 4) =
= k · 1(k) − k · 1(k − 2) + 2 · 1(k − 2) − 2 · 1(k − 4) + k · 1(k − 4) − 2 · 1(k − 4) =
= k · 1(k) − (k − 2) · 1(k − 2) + (k − 4) · 1(k − 4)
Considerando la trasformata zeta della rampa a tempo discreto, ovvero
2
3
Z k · 1(k) =
z
(z − 1)2
e sfruttando la proprietà
2
3
2
3
Z f (k − n) = z −n · Z f (k)
(trasformata zeta di una funzione traslata nel tempo), si ottiene
2
3
2
3
Z (k − 2) · 1(k − 2) = z −2 · Z k · 1(k) =
1
z(z − 1)2
2
3
2
3
Z (k − 4) · 1(k − 4) = z −4 · Z k · 1(k) =
1
z 3 (z − 1)2
Pertanto, la trasformata zeta del segnale in figura è
U (z) =
1
1
z4 − z2 + 1
z
+
+
=
(z − 1)2
z(z − 1)2
z 3 (z − 1)2
z 3 (z − 1)2
Davide Giglio – Esercitazioni di Teoria dei Sistemi – Anno Accademico 2010/2011
20