Capitolo
3
Legge di Ohm
Testi e disegni ideati e realizzati
dal docente
Franco Campagna
3.1. Legge di Ohm
Già a livello intuitivo siamo consapevoli che a parità di tensione elettrica applicata
aumentando la resistenza elettrica del materiale l’intensità di corrente diminuisce.
In figura 3.1.1 nella pagina seguente è rappresentato il simbolo attribuito alla
resistenza con indicata anche la tensione applicata e l’intensità di corrente.
Questa intuizione è confortata da risultati sperimentali che vanno sotto il nome
di Legge di Ohm che di seguito definiamo in modo operativo.
Legge di Ohm: Un materiale avente resistenza elettrica R impone una relazione
direttamente proporzionale tra la tensione V applicata e l’intensità di corrente I che ne scaturisce. A parità di resistenza elettrica R, al raddoppio
della tensione V applicata, raddoppia l’intensità di corrente I.
In formule:
V =R·I
(3.1.1)
31
32
3.1. LEGGE DI OHM
I
V
+
R
Franco
CAMPAGNA
2014
Figura 3.1.1.: Una resistenza elettrica R sottoposta ad una tensione elettrica V è
sede di una intensità di corrente elettrica I.
Dove:
I
• V : Tensione elettrica espressa in [V ];
• R: Resistenza elettrica espressa in [⌦];
• I: Intensità di corrente elettrica espressa
V in [A].
+
R1
Facilmente si possono ricavare le altre due formule -inverse della 3.1.1 nella pagina
precedente:
Franco
CAMPAGNA
2014
V =R·I !
!I =
V
R
1
1
·V = R · I· !
R
R
1
1
V = R · I ! ·V = R · ◆
I· !
I
I
◆
V
!R =
I
(3.1.2)
(3.1.3)
Molto utile per ricordare le formule relative alla Legge di Ohm è far riferimento al disegno di figura 3.1.2 a fronte, nel quale per ricavare la tensione V basta
L’ora di Elettrauto
Franco Campagna
R2
33
CAPITOLO 3. LEGGE DI OHM
Legge di Ohm
V
2014
R
I
V=RI
Franco
CAMPAGNA
+
R=V/I
I
R
V
I=V/R
-
Figura 3.1.2.: Legge di Ohm: triangolo mnemonico, formule e simbolo.
nasconderla nel disegno e scrivere a fianco le lettere rimaste, idem per ricavare la
resistenza e l’intensità di corrente.
3.1.1. Esempi
Esempio 42. Quale valore di resistenza bisogna utilizzare per ottenere una corrente di 1, 5A applicando una tensione di 24V ?
Per ottenere il valore di resistenza richiesto basta applicare l’equazione 3.1.3
nella pagina precedente:
R=
V
24V
=
= 16⌦
I
1, 5A
Esempio 43. Un diodo assorbe 12mA se alimentato a 5V , quale valore di resistenza presenta?
Qualunque sia il componente, se si conosce la corrente assorbita e la tensione di
alimentazione, l’equazione 3.1.3 a fronte della Legge di Ohm permette di calcolare
il valore di resistenza che lo caratterizza:
R=
V
5V
5 ⇥ 103
=
=
= 416, 6⌦
I
12 ⇥ 10 3 A
12
Esempio 44. La lampada da 55W del faro anabbagliante di un’auto assorbe una
corrente di 4, 58A. Qual è il suo valore di resistenza?
Franco Campagna
L’ora di Elettrauto
34
3.1. LEGGE DI OHM
Come per gli altri esempi basta applicare la 3.1.3 a pagina 32:
R=
V
12V
=
= 2, 62⌦
I
4, 58A
Esempio 45. Una resistenza di 32⌦ è sottoposta alla tensione di 12V , il valore
di corrente risulta di’
Per risolvere il quesito basta applicare la 3.1.2 a pagina 32:
I=
V
12V
=
= 0, 375A = 375mA
R
32⌦
Esempio 46. Viene sostituita la lampada di un auto che presenta un valore di
resistenza di 2, 6⌦ con una avente un valore di resistenza dimezzato. La corrente
aumenta o diminuisce? Quanto sarà il nuove valore di corrente rispetto quello con
la lampadina originale?
A parità di tensione elettrica applicata, come nel caso di un’automobile, se diminuisce la resistenza aumenta il valore di intensità di corrente elettrica, in particolare
visto che la relazione è del tipo inversamente proporzionale, al dimezzamento della
resistenza, raddoppia la corrente.
Diamo valore numerico a quanto appena osservato.
Il valore di corrente con la lampada da 2, 6⌦ è:
I1 =
V
12V
=
= 4, 62A
R
2, 6⌦
Il valore di resistenza della lampada nuova, essendo la metà di quella che va a
sostituire, risulta di:
1
1
R2 = R = 2, 6 = 1, 3⌦
2
2
E quindi il nuovo valore di intensità di corrente elettrica vale:
I2 =
V
12V
=
= 9, 23A
R2
1, 3⌦
Quindi si ha un raddoppio della corrente elettrica con probabile intervento del
fusibile a proteggere l’impianto.
L’ora di Elettrauto
Franco Campagna
CAPITOLO 3. LEGGE DI OHM
35
3.1.2. Esercizi
Esercizio 47. Una resistenza di 12⌦ è sottoposta alla tensione di 24V , determinare
la corrente.
[2A]
Esercizio 48. Una tensione di 12V è applicata ad una resistenza la quale impone
una corrente di 3A. Determinare il valore della resistenza.
[4⌦]
Esercizio 49. Una resistenza di 12⌦ è soggetta ad una corrente di 2, 5A, determinare la tensione alla quale è alimentata.
[30V ]
Esercizio 50. Una resistenza di 6⌦ è sottoposta alla tensione di 12V , determinare
la corrente.
[2A]
Esercizio 51. Una tensione di 12V è applicata ad una resistenza la quale impone
una corrente di 4A. Determinare il valore della resistenza.
[3⌦]
Esercizio 52. Una resistenza di 100⌦ è soggetta ad una corrente di 0, 5A, determinare la tensione alla quale è alimentata.
[50V ]
Esercizio 53. Una resistenza di 24⌦ è sottoposta alla tensione di 12V , determinare
la corrente.
[0, 5A]
Esercizio 54. Una tensione di 12V è applicata ad una resistenza la quale impone
una corrente di 6A. Determinare il valore della resistenza.
[2⌦]
Esercizio 55. Una resistenza di 6⌦ è soggetta ad una corrente di 2A, determinare
la tensione alla quale è alimentata.
[12V ]
Franco Campagna
L’ora di Elettrauto
36
3.2. SERIE DI RESISTENZE
I
I
V
+
R1
-
V
+
-
Rs=R1+R2
R2
Franco
CAMPAGNA
2015
Figura 3.2.1.: La resistenza equivalente Rs della serie di due resistente è data dalla
somma delle resistenze: Rs = R1 + R2 .
I=I1=I2=...=In
V
+
-
I1
R1
V
+
-
I2
Rs=R1+...+Rn
R2
Franco
CAMPAGNA
2015
In
Rn
Figura 3.2.2.: La resistenza equivalente Rs della serie di n resistente è data dalla
somma delle n resistenze: Rs = R1 + ... + Rn . Le resistenze in serie
sono interessate dalla medesima intensità di corrente elettrica.
3.2. Serie di resistenze
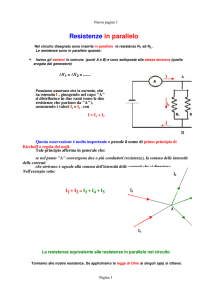
La resistenza equivalente alla serie di due o più resistenze è data dalla somma delle
resistenze, come mostrato nelle figure 3.2.1 e 3.2.2.
Rs = R1 + R2 + . . . + Rn
(3.2.1)
Le resistenze in serie sono interessate dalla medesima intensità di corrente elettrica.
Conoscendo la tensione applicata dal generatore ed il valore delle singole resi-
L’ora di Elettrauto
Franco Campagna
37
CAPITOLO 3. LEGGE DI OHM
-
R1
I1=I
R2
I2=I
V=V1+V2
+
V1
V
V2
I
Franco
CAMPAGNA
2015
Figura 3.2.3.: La somma delle cadute di tensione ai capi delle resistenze in serie è
uguale alla tensione di alimentazione.
stenze è possibile, applicando la Legge di Ohm, calcolare la singola caduta di
tensione (c.d.t.1 ) ai capi di ogni resistenza.
Consideriamo la figura 3.2.3 in cui due resistenze sono alimentate alla tensione
V , per determinare V1 e V2 bisogna affidarsi alla seguente procedura:
• Innanzitutto calcoliamo la resistenza equivalente serie:
Rs = R1 + R2
• Possiamo ora calcolare il valore dell’intensità di corrente elettrica applicando
la Legge di Ohm:
I=
V
Rs
• A questo punto, applicando ripetutamente la Legge di Ohm, possiamo calcolare le due cadute di tensione ai capi delle due resistenze:
V 1 = R1 · I
V 2 = R2 · I
1
La caduta di tensione, acronimo c.d.t., rappresenta quanto della tensione di alimentazione è
impiegata ai capi di un componente. La c.d.t. ai capi di un conduttore ideale è nulla, mentre
è massima ai capi di un isolante ideale.
Franco Campagna
L’ora di Elettrauto
c.d.t.
38
3.2. SERIE DI RESISTENZE
Verifichiamo che la somma delle cadute di tensione ai capi delle resistenze deve
dare ancora la tensione V di alimentazione:
V1 + V2 = R1 · I + R2 · I = I · (R1 + R2 ) = I · Rs = V
3.2.1. Esempi
Esempio 56. Con riferimento alla figura 3.2.3 nella pagina precedente l’alimentazione è quella della batteria di un’auto e le resistenze presentano i seguenti valori:
R1 = 4⌦ e R2 = 8⌦. Si vuole conoscere le cadute di tensione ai capi delle due
resistenze.
Innanzitutto calcoliamo la resistenza equivalente serie:
Rs = R1 + R2 = 4⌦ + 8⌦ = 12⌦
Possiamo ora calcolare il valore dell’intensità di corrente elettrica applicando la
Legge di Ohm:
I=
V
12V
=
= 1A
Rs
12⌦
A questo punto, applicando ripetutamente la Legge di Ohm, possiamo calcolare
le due cadute di tensione ai capi delle due resistenze:
V1 = R1 · I = 4⌦ · 1A = 4V
V2 = R2 · I = 8⌦ · 1A = 8V
Verifichiamo che la somma delle cadute di tensione ai capi delle resistenze deve
dare ancora la tensione V di alimentazione:
V1 + V2 = 4V + 8V = 12V
Esempio 57. Con riferimento alla figura 3.2.4 nella pagina successiva l’alimentazione è quella della batteria di un’auto e le resistenze presentano i seguenti valori:
L’ora di Elettrauto
Franco Campagna
39
CAPITOLO 3. LEGGE DI OHM
R1
I1=I
R2
I2=I
R3
I3=I
V=V1+V2+V3
-
V1
+
V2
V
V3
I
Franco
CAMPAGNA
2015
Figura 3.2.4.: Serie di tre resistenze.
R1 = 4⌦, R2 = 8⌦ e R2 = 12⌦. Si vuole conoscere le cadute di tensione ai capi
delle due resistenze.
Resistenza equivalente serie:
Rs = R1 + R2 + R3 = 4⌦ + 8⌦ + 12⌦ = 24⌦
Intensità di corrente elettrica:
I=
V
12V
=
= 0, 5A
Rs
24⌦
Le cadute di tensione ai capi delle resistenze:
V1 = R1 · I = 4⌦ · 0, 5A = 2V
V2 = R2 · I = 8⌦ · 0, 5A = 4V
V3 = R3 · I = 12⌦ · 0, 5A = 6V
Verifichiamo che la somma delle cadute di tensione ai capi delle resistenze deve
dare ancora la tensione V di alimentazione:
V1 + V2 + V3 = 4V + 8V + 6V = 12V
Franco Campagna
L’ora di Elettrauto
40
3.2. SERIE DI RESISTENZE
3.2.2. Esercizi
Esercizio 58. Due resistenze di 12⌦ e 24⌦ sono collegate in serie e alimentate da
una tensione di 12V . Determinare il valore della resistenza serie, della corrente
che le interessa e delle cadute di tensione ai loro capi.
[36⌦; 0, 33A; 4V ; 8V ]
Esercizio 59. Due resistenze di 6⌦ e 12⌦ sono collegate in serie e alimentate da
una tensione di 24V . Determinare il valore della resistenza serie, della corrente
che le interessa e delle cadute di tensione ai loro capi.
[18⌦; 1, 33A; 8V ; 16V ]
Esercizio 60. Due resistenze di 12⌦ e 12⌦ sono collegate in serie e alimentate da
una tensione di 12V . Determinare il valore della resistenza serie, della corrente
che le interessa e delle cadute di tensione ai loro capi.
[24⌦; 0, 5A; 6V ; 6V ]
Esercizio 61. Due resistenze di 8⌦ e 16⌦ sono collegate in serie e alimentate da
una tensione di 12V . Determinare il valore della resistenza serie, della corrente
che le interessa e delle cadute di tensione ai loro capi.
[24⌦; 0, 5A; 4V ; 8V ]
Esercizio 62. Tre resistenze di 8⌦, 16⌦ e 24⌦ sono collegate in serie e alimentate
da una tensione di 24V . Determinare il valore della resistenza serie, della corrente
che le interessa e delle cadute di tensione ai loro capi.
[48⌦; 0, 5A; 4V ; 8V ; 12V ]
Esercizio 63. Tre resistenze di 4⌦, 16⌦ e 8⌦ sono collegate in serie e alimentate
da una tensione di 12V . Determinare il valore della resistenza serie, della corrente
che le interessa e delle cadute di tensione ai loro capi.
[28⌦; 0, 43A; 1, 71V ; 6, 86V ; 3, 43V ]
Esercizio 64. Quattro resistenze di 8⌦, 16⌦, 24⌦ e 48⌦ sono collegate in serie
e alimentate da una tensione di 12V . Determinare il valore della resistenza serie,
della corrente che le interessa e delle cadute di tensione ai loro capi.
L’ora di Elettrauto
Franco Campagna
41
CAPITOLO 3. LEGGE DI OHM
I
I
V
+
R1
-
V
R2
+
Rp
Franco
CAMPAGNA
2015
Figura 3.3.1.: Parallelo di due resistenze. Rp =
R1 ·R2
R1 +R2
[96⌦; 0, 125A; 1V ; 2V ; 3V ; 6V ]
Esercizio 65. Quattro resistenze di 4⌦, 8⌦, 16⌦ e 32⌦ sono collegate in serie e
alimentate da una tensione di 12V . Determinare il valore della resistenza serie,
della corrente che le interessa e delle cadute di tensione ai loro capi.
[60⌦; 0, 2A; 0, 8V ; 1, 6V ; 3, 2V ; 6, 4V ]
3.3. Parallelo di resistenze
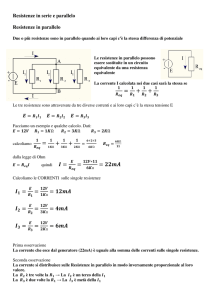
La resistenza equivalente di due resistenze collegate in parallelo come in figura 3.3.1, è data dalla seguente formula:
Rp =
R1 · R2
R1 + R2
(3.3.1)
Se le due resistenze sono uguali la resistenza equivalente parallelo sarà la metà
delle due:
1
2
Rp =
R1 · R2
R·R
R
R
=
=
=
R1 + R2
R+R
2
2R
(3.3.2)
Se le resistenze in parallelo sono più di due come rappresentato in figura 3.3.2
nella pagina successiva, la resistenza equivalente parallelo si calcola con la seguente
formula:
Rp =
Franco Campagna
1
R1
+
1
R2
1
+ ··· +
1
Rn
(3.3.3)
L’ora di Elettrauto
42
3.3. PARALLELO DI RESISTENZE
I
I
V
+
R1
-
R2
V
Rn
+
Rp
Franco
CAMPAGNA
2015
Figura 3.3.2.: Parallelo di più resistenze. Rp =
1
1
+ R1 +···+ R1
R1
n
2
I=I1+I2+...+In
R1
I1
V
I2
R2
Rn
In
+
Franco
Franco
CAMPAGNA
-
Franco
CAMPAGNA
2015
CAMPAGNA
2015
H7 12V 55W
2015
H7 12V 55W
H7 12V 55W
Franco
CAMPAGNA
2015
Figura 3.3.3.: La corrente erogata dal generatore è la medesima che vi rientra
dunque I = I1 + I2 + · · · + In .
Se le n resistenze sono tutte uguali R1 = R2 = · · · = Rn = R, allora la resistenza
equivalente parallelo vale:
Rp =
1
R1
+
1
R2
1
+ ··· +
1
Rn
=
1
R
+
1
R
1
+ ··· +
1
R
=
1
n
R
=
R
n
(3.3.4)
Si può dimostrare e lo verificheremo attraverso gli esercizi, cha la resistenza
equivalente del parallelo di resistenze assume un valore inferiore alla minore delle
resistenze che compongono il parallelo.
Poiché la “corrente” non si disperde nel circuito elettrico, osservando la figura 3.3.3, possiamo dire che la corrente erogata dal generatore deve rientrare in esso
senza perdite:
I = I1 + I2 + · · · + In
(3.3.5)
Con riferimento alla figura 3.3.3 si osservi che tutte le resistenze sono sottoposte
alla stessa tensione.
L’ora di Elettrauto
Franco Campagna
43
CAPITOLO 3. LEGGE DI OHM
I
I1
V
R1
I2
R2
+
Franco
Franco
CAMPAGNA
CAMPAGNA
2015
H7 12V 55W
-
2015
H7 12V 55W
Franco
CAMPAGNA
2015
Figura 3.3.4.: Resistenze collegate in parallelo.
3.3.1. Esempi
Esempio 66. Due resistenze R1 = 6⌦ e R2 = 12⌦ sono collegate in parallelo
come in figura 3.3.4 e alimentate alla tensione di 12V . Determinare la resistenza
equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2
che le interessano.
Per determinare la resistenza equivalente parallelo basta applicare la formula 3.3.1 a pagina 41:
Rp =
R1 · R2
6⌦ · 12⌦
=
= 4⌦
R1 + R2
6⌦ + 12⌦
Ora possiamo calcolare direttamente la corrente I erogata dal generatore attraverso la formula 3.1.2 a pagina 32:
I=
V
12V
=
= 3A
Rp
4⌦
Per calcolare le correnti I1 e I2 nelle due resistenze basta tener presente che
entrambe sono sottoposte alla medesima tensione di alimentazione:
Franco Campagna
I1 =
12V
V
=
= 2A
R1
6⌦
I2 =
V
12V
=
= 1A
R2
12⌦
L’ora di Elettrauto
44
3.3. PARALLELO DI RESISTENZE
E quindi, come calcolato sopra per altra via, la corrente erogata dal generatore
è:
I = I1 + I2 = 2A + 1A = 3A
Esempio 67. Due resistenze R1 = 12⌦ e R2 = 12⌦ sono collegate in parallelo e
alimentate alla tensione di 24V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
La resistenza equivalente parallelo vale:
Rp =
R1 · R2
12⌦ · 12⌦
=
= 6⌦
R1 + R2
12⌦ + 12⌦
confermando numericamente che la resistenza equivalente di due resistenze uguali collegate in parallelo assumerà un valore metà di quello delle due resistenze.
Ecco quindi il motivo per cui collegando due casse acustiche uguali di 8⌦ la
resistenza complessiva sarà di 4⌦ cioè della metà.
La corrente erogata dal generatore vale:
I=
V
24V
=
= 4A
Rp
6⌦
Le correnti I1 e I2 nelle due resistenze risultano essere di:
I1 =
V
24V
=
= 2A
R1
12⌦
I2 =
V
24V
=
= 2A
R2
12⌦
Si conferma che la corrente erogata dal generatore è:
I = I1 + I2 = 2A + 2A = 4A
Esempio 68. Tre resistenze R1 = 4⌦, R2 = 8⌦ e R3 = 16⌦ sono collegate in
parallelo come illustrato in figura 3.3.5 nella pagina successiva e alimentate dalla
batteria di automobile da 12V . Si vuole determinare la resistenza equivalente
parallelo Rp , la corrente I erogata dal generatore e le correnti I1 , I2 e I3 nelle tre
resistenze.
L’ora di Elettrauto
Franco Campagna
45
CAPITOLO 3. LEGGE DI OHM
I
V
I
+
-
I1
I2
I3
R1
R2
R3
I12
V
+
I3
R12
R3
-
Franco
Franco
CAMPAGNA
CAMPAGNA
2015
2015
I
V
+
Rp
Franco
CAMPAGNA
2015
Figura 3.3.5.: Parallelo di 3 resistenze. Se ne può prima calcolare il parallelo di
due e poi il parallelo tra quello trovato e la terza.
Per calcolare la resistenza equivalente parallelo di tre resistenze collegate in
parallelo si può utilizzare direttamente la formula 3.3.3 a pagina 41:
Rp =
1
1
R1
+
1
R2
+
1
R3
=
1
1
4⌦
+
1
8⌦
+
1
16⌦
= 2, 29⌦
Possiamo calcolare la resistenza equivalente parallelo anche applicando la 3.3.1
a pagina 41 ripetutamente:
R1 · R2
4⌦ · 8⌦
=
= 2, 67⌦
R1 + R2
4⌦ + 8⌦
R12 · R3
2, 67⌦ · 16⌦
Rp =
=
= 2, 29⌦
R12 + R3
2, 67⌦ + 16⌦
R12 =
Come si può constatare i risultati con i due metodi coincidono.
Si osservi che la resistenza equivalente parallelo è inferiore della minore delle
resistenze che compongono il parallelo:
Rp < minore {R1 ; R2 ; R3 }
La corrente erogata dal generatore vale:
Franco Campagna
L’ora di Elettrauto
46
3.3. PARALLELO DI RESISTENZE
I2=0A
I
R2
I1
V
+
R1
-
Franco
CAMPAGNA
2015
H7 12V 55W
Franco
CAMPAGNA
2015
Cortociruito
Figura 3.3.6.: Corto circuito con correnti elevatissime che interessano il corto
circuito stesso e l’alimentazione.
I=
V
12V
=
= 5, 24A
Rp
2, 29⌦
Le correnti nelle tre resistenze risultano essere di:
V
12V
=
= 3A
R1
4⌦
V
12V
I2 =
=
= 1, 5A
R2
8⌦
V
12V
I3 =
=
= 0, 75A
R3
16⌦
I1 =
La corrente erogata dal generatore risulta:
I = I1 + I2 + I3 = 3A + 1, 5A + 0, 75A = 5, 25A
Esempio 69. Se una resistenza R2 = 1k⌦, alimentata da batteria per auto da 12V ,
viene cortocircuitata da un conduttore che sappiamo avere resistenza praticamente
nulla (R1 = 0⌦) come mostrato in figura 3.3.6, la resistenza equivalente parallelo
risulterà anch’essa nulla.
Infatti:
L’ora di Elettrauto
Franco Campagna
47
CAPITOLO 3. LEGGE DI OHM
Rp =
R1 · R2
0⌦ · 1k⌦
0
=
= = 0⌦
R1 + R2
0⌦ + 1k⌦
1
E quindi la corrente erogata dal generatore risulta:
I=
V
12V
=
! 1A
Rp
0⌦
Quindi la batteria dovrebbe erogare una corrente infinita. Se non interviene
una protezione quale un fusibile, si può avere la fusione dei conduttori ad anche
l’esplosione della batteria.
Esempio 70. Un’automobile monta due proiettori anabbaglianti uno sul lato sinistro anteriore del veicolo (acronimo SX) e uno sul lato destro (acronimo DX)
con le seguenti caratteristiche:
• Proiettore abbagliante:
– Potenza: 60W
– Resistenza: RSX60 = RDX60 = 2, 4⌦
Si vuole aggiungere altri due proiettori potenziati, come mostrato in figura 3.3.7,
aventi le seguenti caratteristiche:
• Proiettore abbagliante potenziato:
– Potenza: 100W
– Resistenza: RSX100 = RDX100 = 1, 444⌦
Tutti i proiettori sono alimentati dalla batteria dell’auto a 12V .
Si vuole conoscere quanto segue:
1. La corrente erogata dalla batteria con i soli proiettori da 60W
2. La corrente erogata dalla batteria aggiungendo i proiettori potenziati da
100W
3. La corrente erogata dalla batteria con i soli proiettori potenziati da 100W
Franco Campagna
L’ora di Elettrauto
48
3.3. PARALLELO DI RESISTENZE
I
Isx
Isx60
V
RSX60
RSX100
Idx
Isx100
RSX100
RSX60
Isx100
+
Franco
Franco
CAMPAGNA
CAMPAGNA
2015
2015
H7 12V 55W
-
Isx60
Franco
Franco
CAMPAGNA
CAMPAGNA
2015
H7 12V 55W
Isx
H7 12V 55W
2015
H7 12V 55W
Idx
Franco
CAMPAGNA
2015
I
Figura 3.3.7.: Impianto abbagliante di un automobile con aggiunta di proiettori
potenziati.
Caso 1.
Per il primo caso basta calcolare la resistenza equivalente parallelo dei
due proiettori da 60W :
RP 60 =
RSX60
2, 4⌦
=
1, 2⌦
2
2
quindi la corrente I erogata dalla batteria sarà di:
I1 =
Caso 2.
12V
V
=
= 10A
RP 60
1, 2⌦
Nel secondo caso invece si collegano in parallelo anche gli altri due proiettori potenziati. Calcoliamo prima la resistenza equivalente parallelo
dei due proiettori potenziati:
RP 100 =
RSX100
1, 44⌦
=
= 0, 72⌦
2
2
Per determinare la resistenza equivalente parallelo dei quattro proiettori
L’ora di Elettrauto
Franco Campagna
49
CAPITOLO 3. LEGGE DI OHM
basta calcolare il parallelo di RP 60 e RP 100 :
RP 60/100 =
RP 60 · RP 100
1, 2 · 0, 72
=
= 0, 45⌦
RP 60 + RP 100
1, 2 + 0, 72
La corrente erogata dalla batteria con i quattro proiettori accesi risulta
essere di:
V
12V
I2 =
=
= 26, 67A
RP 60/100
0, 45⌦
Quindi con un incremento di corrente di oltre due volte e mazza e
dunque andrà verificata la taglia del fusibile di protezione.
Caso 3.
Nel terzo caso per determinare la corrente erogata dalla batteria basterà
utilizzare la resistenza equivalente parallelo dei proiettori potenziati già
calcolata:
V
12V
I3 =
=
= 16, 67A
RP 100
0, 72⌦
Quindi con un incremento di circa il 70% di corrente rispetto ai proiettori originali.
Questo esempio pone in evidenzia come il modificare l’impianto elettrico preesistente impone degli attenti controlli sulle correnti in gioco e sulla necessità di
verificare l’adeguatezza delle protezioni (fusibili) e della sezione dei conduttori.
3.3.2. Esercizi
Esercizio 71. Due resistenze R1 = 6⌦ e R2 = 6⌦ sono collegate in parallelo e
alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[3⌦; 4A; 2A; 2A]
Esercizio 72. Due resistenze R1 = 1⌦ e R2 = 11⌦ sono collegate in parallelo e
alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[0, 92⌦; 13, 09A; 12A; 1, 09A]
Franco Campagna
L’ora di Elettrauto
50
3.3. PARALLELO DI RESISTENZE
Esercizio 73. Due resistenze R1 = 12⌦ e R2 = 24⌦ sono collegate in parallelo
e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[38⌦; 1, 5A; 1A; 0, 5A]
Esercizio 74. Due resistenze R1 = 6⌦ e R2 = 18⌦ sono collegate in parallelo e
alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[4, 5⌦; 2, 67A; 2A; 0, 67A]
Esercizio 75. Due resistenze R1 = 24⌦ e R2 = 48⌦ sono collegate in parallelo
e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[16⌦; 0, 75A; 0, 5A; 0, 75A]
Esercizio 76. Due resistenze R1 = 24⌦ e R2 = 24⌦ sono collegate in parallelo
e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[12⌦; 1A; 0, 5A; 0, 5A]
Esercizio 77. Due resistenze R1 = 2⌦ e R2 = 4⌦ sono collegate in parallelo e
alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[1, 3⌦; 9A; 6A; 3A]
Esercizio 78. Due resistenze R1 = 4⌦ e R2 = 4⌦ sono collegate in parallelo e
alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[2⌦; 6A; 3A; 3A]
Esercizio 79. Due resistenze R1 = 24⌦ e R2 = 12⌦ sono collegate in parallelo
e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
L’ora di Elettrauto
Franco Campagna
CAPITOLO 3. LEGGE DI OHM
51
[8⌦; 1, 5A; 0, 5A; 1A]
Esercizio 80. Due resistenze R1 = 48⌦ e R2 = 24⌦ sono collegate in parallelo
e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[16⌦; 0, 75A; 0, 25A; 0, 5A]
Esercizio 81. Due resistenze R1 = ⌦ e R2 = ⌦ sono collegate in parallelo e
alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[⌦; A; A; A]
Esercizio 82. Due resistenze R1 = 4⌦ e R2 = 8⌦ sono collegate in parallelo e
alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[2, 67⌦; 4, 5A; 3A; 1, 5A]
Esercizio 83. Due resistenze R1 = 6⌦ e R2 = 12⌦ sono collegate in parallelo e
alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[4⌦; 3A; 2A; 1A]
Esercizio 84. Due resistenze R1 = 2⌦ e R2 = 8⌦ sono collegate in parallelo e
alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[1, 6⌦; 7, 5A; 6A; 1, 5A]
Esercizio 85. Tre resistenze R1 = 2⌦, R2 = 4⌦ e R3 = 8⌦ sono collegate in
parallelo e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le
interessano.
[1, 14⌦; 10, 05A; 6A; 3A; 1, 5A]
Franco Campagna
L’ora di Elettrauto
52
3.3. PARALLELO DI RESISTENZE
Esercizio 86. Due resistenze R1 = 1⌦ e R2 = 100⌦ sono collegate in parallelo
e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo
Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le interessano.
[0, 99⌦; 12, 12A; 12A; 0, 12A]
Esercizio 87. Tre resistenze R1 = 4⌦, R2 = 4⌦ e R3 = 2⌦ sono collegate in
parallelo e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le
interessano.
[1⌦; 12A; 3A; 3A; 6A]
Esercizio 88. Tre resistenze R1 = 24⌦, R2 = 12⌦ e R3 = 24⌦ sono collegate
in parallelo e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le
interessano.
[6⌦; 2A; 0, 5A; 1A; 0, 5A]
Esercizio 89. Tre resistenze R1 = 48⌦, R2 = 24⌦ e R3 = 48⌦ sono collegate
in parallelo e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le
interessano.
[12⌦; 1A; 0, 25A; 0, 5A; 0, 25A]
Esercizio 90. Tre resistenze R1 = 4⌦, R2 = 8⌦ e R3 = 12⌦ sono collegate in
parallelo e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le
interessano.
[2, 18⌦; 5, 5A; 3A; 1, 5A; 1A]
Esercizio 91. Tre resistenze R1 = 12⌦, R2 = 48⌦ e R3 = 12⌦ sono collegate
in parallelo e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le
interessano.
L’ora di Elettrauto
Franco Campagna
CAPITOLO 3. LEGGE DI OHM
53
[3, 69⌦; 3, 25A; 2A; 1A; 0, 25A]
Esercizio 92. Tre resistenze R1 = 2⌦, R2 = 8⌦ e R3 = 16⌦ sono collegate in
parallelo e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le
interessano.
[1, 45⌦; 8, 25A; 6A; 1, 5A; 0, 75A]
Esercizio 93. Tre resistenze R1 = 1⌦, R2 = 10⌦ e R3 = 100⌦ sono collegate
in parallelo e alimentate alla tensione di 12V . Determinare la resistenza equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2 che le
interessano.
[0, 9⌦; 13, 32A; 12A; 1, 2A; 0, 12A]
Esercizio 94. Quattro resistenze R1 = 2⌦, R2 = 4⌦, R3 = 8⌦ e R4 = 16⌦ sono
collegate in parallelo e alimentate alla tensione di 12V . Determinare la resistenza
equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2
che le interessano.
[1, 067⌦; 11, 25A; 6A; 3A; 1, 5A; 0, 75A]
Esercizio 95. Quattro resistenze R1 = 4⌦, R2 = 4⌦, R3 = 2⌦ e R4 = 2⌦ sono
collegate in parallelo e alimentate alla tensione di 12V . Determinare la resistenza
equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2
che le interessano.
[0, 67⌦; 18A; 3A; 3A; 6A; 6A]
Esercizio 96. Quattro resistenze R1 = 24⌦, R2 = 12⌦, R3 = 24⌦ e R4 =
12⌦ sono collegate in parallelo e alimentate alla tensione di 12V . Determinare
la resistenza equivalente parallelo Rp , la corrente I erogata dal generatore e le
correnti I1 e I2 che le interessano.
[4⌦; 3A; 0, 5A; 1A; 0, 5A; 1A]
Franco Campagna
L’ora di Elettrauto
54
3.4. CORTO CIRCUITO
Esercizio 97. Quattro resistenze R1 = 48⌦, R2 = 24⌦, R3 = 48⌦ e R4 =
24⌦ sono collegate in parallelo e alimentate alla tensione di 12V . Determinare
la resistenza equivalente parallelo Rp , la corrente I erogata dal generatore e le
correnti I1 e I2 che le interessano.
[8⌦; 1, 5A; 0, 25A; 0, 5A; 0, 25A; 0, 5A]
Esercizio 98. Quattro resistenze R1 = 4⌦, R2 = 8⌦, R3 = 12⌦ e R4 = 16⌦ sono
collegate in parallelo e alimentate alla tensione di 12V . Determinare la resistenza
equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2
che le interessano.
[1, 92⌦; 6, 25A; 3A; 1, 5A; 1A; 0, 75A]
Esercizio 99. Quattro resistenze R1 = 6⌦, R2 = 12⌦, R3 = 48⌦ e R4 = 96⌦sono
collegate in parallelo e alimentate alla tensione di 12V . Determinare la resistenza
equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2
che le interessano.
[3, 56⌦; 3, 375A; 2A; 1A; 0, 25A; 0, 125A]
Esercizio 100. Quattro resistenze R1 = 2⌦, R2 = 8⌦, R3 = 16⌦ e R4 = 48⌦ sono
collegate in parallelo e alimentate alla tensione di 12V . Determinare la resistenza
equivalente parallelo Rp , la corrente I erogata dal generatore e le correnti I1 e I2
che le interessano.
[1, 41⌦; 8, 5A; 6A; 1, 5A; 0, 75A; 0, 25A]
Esercizio 101. Quattro resistenze R1 = 1⌦, R2 = 10⌦, R3 = 100⌦ e R4 =
1000⌦ sono collegate in parallelo e alimentate alla tensione di 12V . Determinare
la resistenza equivalente parallelo Rp , la corrente I erogata dal generatore e le
correnti I1 e I2 che le interessano.
[0, 9⌦; 13, 332A; 12A; 1, 22A; 0, 12A; 0, 012A]
L’ora di Elettrauto
Franco Campagna
55
CAPITOLO 3. LEGGE DI OHM
I2=0A
I
R2
I1
V
+
R1
-
Franco
CAMPAGNA
2015
H7 12V 55W
Franco
CAMPAGNA
2015
Cortociruito
Figura 3.4.1.: Corto circuito.
3.4. Corto circuito
Si osservi la figura 3.4.1, in cui un conduttore elettrico di resistenza teorica nulla
(Rconduttore = 0⌦) è posto in parallelo ad una lampada (Rlampada 6= 0⌦):
La resistenza parallelo dunque sarà:
RP =
Rlampada · RConduttore
Rlampada · 0⌦
0
=
=
= 0⌦
Rlampada + Rconduttore
Rlampada + 0⌦
Rlampada
(3.4.1)
A questo punto la corrente erogata dalla batteria, teoricamente, dovrebbe assumere il seguente valore:
I=
V
V
=
!1
RP
0⌦
(3.4.2)
In pratica le correnti di corto circuito nelle batterie, se non interrotte da opportune protezioni quali i fusibili, innescano delle violente reazioni chimiche con
produzione di gas che aumentano la pressione dentro l’involucro causandone a volte
il cedimento con un effetto esplosivo.
Diamo ora una definizione operativa del “corto circuito”:
• Corto circuito: si ha cortocircuito tra due punti del circuito elettrico
quando tra essi la resistenza è nulla.
Franco Campagna
L’ora di Elettrauto
56
3.5. DA RICORDARE
3.5. Da ricordare
'
$
• Legge di Ohm
– Vi è proporzionalità diretta tra la tensione e la corrente che interessano
una resistenza
Legge di Ohm
V
2014
R
I
V=RI
Franco
CAMPAGNA
+
R=V/I
I
R
V
I=V/R
-
• Serie di resistenze
– Due o più resistenze sono in serie quando interessate dalla stessa
corrente: Rs = R1 + R2 + · · · + Rn
I=I1=I2=...=In
V
+
-
I1
R1
V
+
-
I2
R2
In
Rn
Rs=R1+...+Rn
Franco
CAMPAGNA
2015
• Parallelo di resistenze
– Due o più resistenze sono collegate in parallelo quando sottoposte alla
·R2
stessa tensione: R12 = RR11+R
, Rp = 1 + 1 1+···+ 1
2
R1
R2
Rn
I
I
V
+
-
R1
R2
Rn
V
+
Rp
Franco
CAMPAGNA
2015
• Corto circuito
– Si ha cortocircuito tra due punti dell’impianto quando tra essi la
resistenza è nulla
&
%
L’ora di Elettrauto
Franco Campagna
CAPITOLO 3. LEGGE DI OHM
57
3.6. Esercizi
Esercizio 102. Indica le tre formule della Legge di Ohm aiutandoti anche con il
diagramma mnemonico:
1. V=
2. I=
3. R=
Esercizio 103. Cosa significa “corto circuito”:
Esercizio 104. Che valore teorico assume la corrente elettrica se metto in corto
circuito i morsetti della batteria dell’auto come in figura:
I2=0A
I
I1
V
+
R1
-
R2
Franco
CAMPAGNA
2015
H7 12V 55W
Franco
CAMPAGNA
2015
Cortociruito
I=
Esercizio 105. Calcola la tensione ai capi di una resistenza da 24⌦ percorsa da
una corrente di 1, 5A.
[36V ]
Esercizio 106. Calcola la corrente che circola in una resistenza da 24⌦ sottoposta
ad una tensione di 48V .
[2A]
Franco Campagna
L’ora di Elettrauto
58
3.6. ESERCIZI
Esercizio 107. Calcola il valore di resistenza di una lampada che sottoposta a
24V assorbe una corrente di 2, 4A.
[10⌦]
Esercizio 108. Completa la figura con i valori mancanti sapendo che R1 = 6⌦,
R2 = 18⌦ e V = 12V :
I=...
V
I12=...
+
I1=...
R1
-
V
+
-
R2
Rs=....
I2=...
Franco
CAMPAGNA
2015
Esercizio 109. Completa la figura con i valori mancanti sapendo che R1 = 4⌦,
R2 = 8⌦, R3 = 12⌦ e V = 24V :
I=...
V
+
-
I12=...
R1
I1=...
V
+
-
R2
I2=...
R3
I3=...
Rs=....
Franco
CAMPAGNA
2015
Esercizio 110. Completa la figura con i valori mancanti sapendo che R1 = 48⌦,
R2 = 48⌦ e V = 24V :
L’ora di Elettrauto
Franco Campagna
59
CAPITOLO 3. LEGGE DI OHM
I=...
I1=...
V
+
-
Ip=...
I2=...
R1
V
R2
+
Rp=...
Franco
CAMPAGNA
2015
Esercizio 111. Completa la figura con i valori mancanti sapendo che R1 = 36⌦,
R2 = 12⌦ e V = 24V :
+
-
R1
I1=...
V1=...
V
R2
I2=...
V2=...
I=...
Franco
CAMPAGNA
2015
Esercizio 112. Completa la figura con i valori mancanti sapendo che R1 = 12⌦,
R2 = 6⌦, R3 = 12⌦ e V = 12V :
I=...
V
+
-
I1=...
I2=...
I3=...
R1
R2
R3
Ip=...
V
+
Rp=...
Franco
CAMPAGNA
2015
Franco Campagna
L’ora di Elettrauto