Triangoli rettangoli
Teoria in sintesi
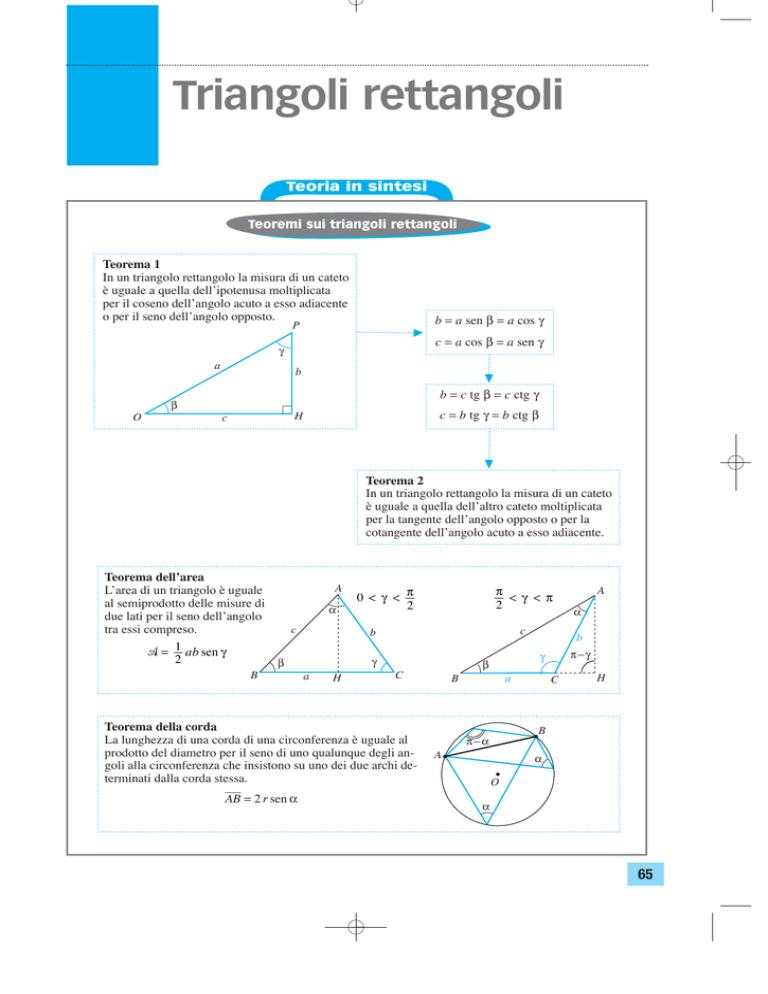
Teoremi sui triangoli rettangoli
Teorema 1
In un triangolo rettangolo la misura di un cateto
è uguale a quella dellipotenusa moltiplicata
per il coseno dellangolo acuto a esso adiacente
o per il seno dellangolo opposto.
b = a sen β = a cos γ
P
c = a cos β = a sen γ
γ
a
b
b = c tg β = c ctg γ
β
O
c = b tg γ = b ctg β
H
c
Teorema 2
In un triangolo rettangolo la misura di un cateto
è uguale a quella dellaltro cateto moltiplicata
per la tangente dellangolo opposto o per la
cotangente dellangolo acuto a esso adiacente.
Teorema dellarea
Larea di un triangolo è uguale
al semiprodotto delle misure di
due lati per il seno dellangolo
tra essi compreso.
� = 1 ab sen γ
2
A
α
c
c
b
γ
β
B
a
H
B
A
α
b
π −γ
γ
β
C
Teorema della corda
La lunghezza di una corda di una circonferenza è uguale al
prodotto del diametro per il seno di uno qualunque degli angoli alla circonferenza che insistono su uno dei due archi determinati dalla corda stessa.
AB = 2 r sen α
π < γ < π
2
0 < γ < π
2
a
C
H
B
π−α
A
α
O
α
65
Triangoli rettangoli
Obiettivo
1
Risoluzione dei triangoli rettangoli
sercizio risolto
Indicando con a la misura dellipotenusa, con b e c le misure dei cateti, con β e γ le ampiezze degli angoli opposti a b e c, risolvere i triangoli di cui sono dati i seguenti elementi:
a = 35
β= π
3
Utilizzando la relazione b = a sen β = 35 sen π , si ha: b = 35 3 .
3
2
Utilizzando la relazione c = a cos β = 35 cos π , si ha: c = 35 . Poiché β + γ = π , si ha: γ = π .
3
2
2
6
sercizi guidati
Indicando con a la misura dellipotenusa, con b e c le misure dei cateti, con β e γ le ampiezze degli
angoli opposti a b e c, risolvere i triangoli di cui sono dati gli elementi indicati.
1. a = 2 2
b=
6
�
b
Utilizzando la relazione b = a sen β, si ha: sen β = =
a
.......................
da cui: β = ............... e cos β = ............... .
π
Utilizzando la relazione c = a cosβ, si ha: c = ............... . Poiché β + γ = , si ha: γ = ............... .
2
2. b = 12
c=5
�
Utilizzando la relazione b = c tg β, si ha: tg β = ............ .
Da cos 2 β + sen 2 β = 1 si ricava: cos β = ............ , sen β = ............ , da cui: cos γ = ............ , sen γ = ............ .
Utilizzando il teorema di Pitagora o la relazione b = a sen β, si ha: a = ............ .
Indicando con a la misura dellipotenusa, con b e c le misure dei cateti, con β e γ le ampiezze degli
angoli opposti a b e c, risolvere i triangoli di cui sono dati i seguenti elementi.
3.7 a = 2 6
�
γ = π
3
8.7 a = 6
b=3 3
4.7 a = 40
b = 20
9.7 b = 15
c=
5.7 a = 5 2
c=5
10. a = 25
b=7
6.7 a = 8
β= π
4
11. a = 15
�
�
tg γ = 3
4
7.7 b = 2
c=2 3
12. c = 4 15
sen γ =
�
�
�
66
�
�
�
�
5
15
4
Triangoli rettangoli
Obiettivo
2
Risoluzione di semplici problemi sui triangoli rettangoli
sercizio risolto
Determinare larea e il perimetro di un triangolo rettangolo, sapendo che lipotenusa è lunga 40 cm
e che sen β = 1 , essendo β uno degli angoli acuti del triangolo.
4
Utilizzando la relazione b = a senβ, si ha: b = 40 1 = 10 cm.
4
Utilizzando il teorema di Pitagora o la relazione c = a cos β = 40 15 , si ha: c = 10 15 cm.
4
Il perimetro è quindi 2 p = 40 + 10 + 10 15 = 50 + 10 15 cm.
Larea è � = 10 ⋅ 10 15 = 50 15 cm 2 .
2
sercizi guidati
13. Determinare larea di un rombo di lato 12 cm, sapendo che un angolo misura 2 π.
3
�
Il rombo è costituito da 4 triangoli rettangoli uguali di ipotenusa lunga ............... e con un angolo acuto
β = ............... .
..........................
cm. Utilizzando la relazione c = a cos β,
si ha: c = .......................... cm.
Larea del rombo è data da: � = 2 b ⋅ 2 c =
2
.................
= ................. cm2.
14. In una circonferenza di diametro AB = 18 cm, tracciare la corda CD perpendicolare al diame = π . Determinare la lunghezza della corda CD e il lato del
tro AB e tale che langolo CAB
3
quadrato equivalente al quadrilatero ACBD.
�
Facendo riferimento alla figura a lato, si ha che il triangolo ABC
C
è ................................. in ................. .
Quindi: CA = AB ⋅ cos CAB = ................. .
A
Il triangolo AHB è ................................. in H.
H
O
B
Quindi: CH = CA ⋅ sen CAB = ................. e CD = ................. .
Il quadrilatero ACBD ha area � = AB ⋅ CD =
2
Il lato del quadrato è dato da: l =
81 3 =
.................
..................
cm2.
D
cm.
67
© RCS Libri S.p.A. - Divisione Education, Milano
Utilizzando la relazione b = a sen β, si ha: b =
Triangoli rettangoli
15. Determinare larea e il perimetro di un triangolo rettangolo, sapendo che lipotenusa è lunga
�
60 cm e che sen β = 3 , essendo β uno degli angoli acuti del triangolo.
5
16. Determinare larea e il perimetro di un triangolo rettangolo, sapendo che laltezza relativa al
lipotenusa è lunga 12 cm e che forma con uno dei cateti un angolo di coseno pari a 4 .
5
2
17. In un triangolo isoscele langolo al vertice è π e il lato obliquo misura 6 cm. Determinare
3
�
larea e il perimetro del triangolo.
�
18. La proiezione dombra di un palo piantato verticalmente sul terreno è 232 cm. Calcolare laltezza del palo sapendo che i raggi cadono a 56° con il terreno (utilizzare la calcolatrice).
�
19. Determinare i cateti di un triangolo rettangolo, sapendo che larea vale 45 cm2 e che la tangente di uno dei suoi angoli acuti è 1 .
4
20. In un triangolo isoscele, il coseno degli angoli alla base vale 4 e la base misura 16 cm.
5
�
Determinare le misure delle tre altezze del triangolo e la sua area.
�
21. Determinare la misura delle diagonali e il perimetro di un rombo ABCD, sapendo che langolo
= π e che il punto O di incontro delle diagonali dista dal lato BC 20 cm.
ACB
6
�
22. In una semicirconferenza di diametro AB = 10 cm e centro O, è data una corda AD tale che
= 3 . Tracciata la tangente in D alla semicirconferenza, sia C il punto di incontro tra
sen BAD
5
la tangente e il prolungamento di AB. Calcolare il perimetro del triangolo ACD.
�
D
A
O
B
C
23. In una circonferenza di diametro AC = 4 cm è inscritto il quadrilatero ABCD. Langolo
ACB = γ è tale che sen γ = 4 e il lato AD = 2 2 cm. Determinare il perimetro e larea del
5
quadrilatero.
�
24. A un punto materiale sono applicate le forze di intensità F1 = 4 3 N e F2 = 8 6 N tra loro
perpendicolari. Determinare la risultante in modulo, direzione e verso.
�
68
Triangoli rettangoli
Obiettivo
3
Calcolare l’area di un triangolo
sercizio risolto
Determinare larea di un parallelogramma, sapendo che le misure di due suoi lati consecutivi sono
5 .
13 e 22 cm e che langolo acuto tra essi compreso ha la tangente uguale a
12
Per calcolare larea si utilizza la relazione � = 1 a b sen γ , poi si moltiplica il valore ottenuto per 2.
2
Sapendo che tg γ = 5 e che cos 2 γ + sen 2 γ = 1, si ottiene cos γ = 12 e sen γ = 5 .
12
13
13
5
Quindi larea del parallelogramma è � = a b sen γ = 13 ⋅ 22 ⋅
= 110 cm 2 .
13
sercizio guidato
25. Determinare larea del dodecagono regolare in funzione del
�
raggio della circonferenza circoscritta.
Si considera il dodecagono costituito da ............... triangoli isosceli uguali, di lato r e angolo al vertice ............... .
r
O
Larea del dodecagono è pari a 12 volte larea di ogni triangolo, quindi si ha: � = ............................... cm2.
26. Determinare larea di un triangolo, sapendo che le misure di due suoi lati consecutivi sono 9 e
�
40 cm e che langolo acuto tra essi compreso ha il coseno uguale a 3 .
5
27. Determinare larea di un parallelogramma, sapendo che le misure di due suoi lati consecutivi
�
sono 13 e 28 cm e che langolo tra essi compreso ha il coseno uguale a − 4 .
7
28. Determinare in funzione del raggio della circonferenza circoscritta, larea dellottagono regolare.
�
29. Determinare larea del triangolo ABC, sapendo che AB = 5 3 cm, AC = 8 cm, cos C = 3 ,
3
2
�
tg B = 3 .
4
30. La diagonale AC = 4 cm del quadrilatero ABCD lo divide nel triangolo ABC, rettangolo in C e
= CAB
= π , calcolare larea e il
nel triangolo isoscele ACD, di base AC. Sapendo che DAC
6
perimetro del quadrilatero.
�
69
Triangoli rettangoli
Obiettivo
4
Applicare il teorema della corda
sercizio risolto
In una circonferenza di centro O e raggio r sono date due corde consecutive AB = 2 r e BC = 6 r.
3
5
Calcolare larea del triangolo ABC.
Per calcolare larea, si utilizza la relazione � = 1 a b sen γ.
2
Si ha: sen γ = sen (α1 + α 2 ), dove α1 e α2 sono gli angoli acuti alla
circonferenza che insistono sulle due corde assegnate. Utilizzando la
formula inversa del teorema della corda, si ha:
C
B
A
r
O
sen α1 = AB = 1 ⇒ cos α1 = 2 2
2r
3
3
sen α 2 = BC = 3 ⇒ cos α 2 = 4
5
2r
5
2( 2 + 3 2 )
sen γ = sen (α1 + α 2 ) = 1 ⋅ 4 + 2 2 ⋅ 3 =
3 5
3 5
15
1 2 6 2( 2 + 3 2 ) = 4 ( 2 + 3 2 ) r2.
Larea è quindi: � = ⋅ r ⋅ r ⋅
2 3 5
15
75
31. Determinare la lunghezza di una corda AB di una circonferenza di raggio r = 5 cm, sapendo
�
= 7 , essendo C un punto della circonferenza.
che sen ACB
25
32. In una circonferenza di centro O e raggio r è data la corda AB = 6 r. Determinare langolo
5
�
alla circonferenza che insiste sulla corda AB.
33. In una circonferenza di centro O e raggio r è data la corda AB = 5 r. Determinare le fun2
�
zioni goniometriche dellangolo convesso AOB.
34. Determinare il lato del dodecagono regolare inscritto in una circonferenza di raggio 6 cm.
�
35. In una circonferenza di centro O e raggio r è data la corda AB, sulla quale si costruisce un
�
triangolo equilatero ABC, non contenente il centro della circonferenza, la cui area vale 3 r 2 .
3
Determinare langolo alla circonferenza che insiste sulla corda AB.
36. Determinare il perimetro dellottagono regolare in funzione del raggio della circonferenza cir�
coscritta.
37. In una circonferenza di centro O e raggio r sono date due corde consecutive AB = 5 r e
2
�
BC = 2 r. Calcolare larea del triangolo ABC.
70
Triangoli rettangoli
Obiettivo
5
Applicare i teoremi studiati a problemi di geometria piana
PROBLEMI SVOLTI PER PUNTI (DA COMPLETARE ALGEBRICAMENTE)
38. In una semicirconferenza di centro O e diametro AB = 2r, tracciare la tangente condotta da A e
�
considerare su essa un segmento AD = 2 3 r. Congiunto D con B, sia M lintersezione tra il
3
segmento DB e la semicirconferenza. Calcolare il perimetro e larea del triangolo ABM.
Risoluzione per punti
Applicare il teorema dei triangoli rettangoli per determinare
langolo ABD.
Osservare che il triangolo ABM è rettangolo.
Applicare il teorema della corda o dei triangoli rettangoli e calcolare AM e BM.
Calcolare larea e il perimetro.
D
M
A
O
B
39. In un trapezio ABCD si ha: AD = DC = 2a, cos ADC = − 7 e cos DCB = − 3 . Determinare la25
5
�
rea e il perimetro del trapezio.
Risoluzione per punti
Ricordare che in un trapezio gli angoli adiacenti ai lati obliqui sono a due a due supplementari.
Indicare con CH e DK le altezze del trapezio; applicare il teorema dei triangoli rettangoli ad ADK e
calcolare CH = DK e AK.
Applicare il teorema dei triangoli rettangoli a HBC e calcolare CB e HB.
Determinare AB = AK + CD + HB.
Calcolare area e perimetro.
40. In una semicirconferenza di centro O e diametro AB = 2r è inscritto un trapezio isoscele ABCD.
�
I lati obliqui sono tali che AD = BC = 2 r. Determinare larea e il perimetro del triangolo BCD.
3
Risoluzione per punti
Applicare il teorema della corda per determinare le funzioni goniometriche di ABD.
Osservare che il triangolo ADB è rettangolo e dedurre le funzioni goniometriche di DAB.
Calcolare la lunghezza della corda DB.
Indicare con CH e DK le altezze del trapezio; calcolare DC = 2r − 2AK dopo aver risolto il triangolo
rettangolo ADK.
Determinare il perimetro del triangolo BCD.
1
.
, essendo BDC
= π − DAB
Determinare larea: � = DC ⋅ CH oppure � = DB ⋅ DC ⋅ sen BDC
2
2
2
41. In una circonferenza di centro O e raggio r sono date tre corde consecutive AB = r, BC = 3 r,
CD = 4 r. Dimostrare che i punti A e C sono diametralmente opposti, calcolare larea del qua5
drilatero ABCD e determinare la lunghezza della corda AD.
�
71
Triangoli rettangoli
Risoluzione per punti
Applicare il teorema della corda per determinare le funzioni goniometriche degli angoli in figura indicati con β1, β2, γ1.
Osservare che β2 è complementare di β1 e quindi AC è un diametro. Di
conseguenza, γ2 = ABD è complementare di γ1.
Calcolare larea del triangolo ABC, rettangolo in B.
Osservare che γ2 = ABD = ACD perché angoli alla circonferenza che
insistono sulla stessa corda AD.
Calcolare larea del triangolo ACD con il teorema dellarea.
Determinare AD con il teorema della corda.
B
γ 2 γ1
A
γ2
O
β1 β2
D
Teoria in sintesi
Geometria nello spazio
Teorema delle tre perpendicolari
Sia r una retta perpendicolare al piano α
e sia P il suo piede; se da P si conduce
la perpendicolare n a una qualunque
retta s del piano α, questultima risulta
perpendicolare al piano individuato
da r e da n.
r
R
P
s
U
α
Posizione relativa
tra due rette nello spazio
n
V
Q
�
Complanari incidenti
parallele
Non complanari o sghembe
Posizione relativa
tra retta e piano
Secanti un punto in comune
Paralleli nessun punto in comune
la retta giace sul piano
Posizione relativa
tra due piani
Secanti una retta in comune
Paralleli coincidenti
nessun punto in comune
�
�
I solidi
Principio di Cavalieri
Due solidi sono equivalenti se:
appoggiati allo stesso piano hanno la stessa altezza;
le loro sezioni ottenute con piani paralleli a quello di appoggio sono equivalenti.
72
C
Triangoli rettangoli
Definizione
Figura solida
Prisma
α′
A′
E′
D′
B′
C′
altezza
→
v
D
E
A
α
C
B
Parallelepipedo
H
G
E
F
d
c
D
A
B b
a
Cubo
H
F
d
D
C
a
A
Piramide
B
b
V
ap
h
C
K
α
B
r
r O
D
H
A
Cilindro
r
r
α
V
α
h
a
Sfera
O
α
ap
r
O
r
Si chiama parallelepipedo un prisma avente per basi due parallelogrammi. Un paralle- Sl = 2 p ⋅ h
lepipedo retto che ha per basi due rettan- St = Sl + 2 Sb
goli si chiama parallelepipedo rettangolo. � = Sb ⋅ h
d =
a2 + b2 + c2
Considerato su un piano α un poligono
ABCD... e preso un punto V ∉α, si definisce
2
2
piramide di vertice V e base ABCD... la parte a = h + r
dellangoloide VABCD... che, rispetto al pia- Sl = p ⋅ a
no α, giace dalla stessa parte del vertice V.
St = St + Sb
Una piramide si dice retta se ha per base
S ⋅h
un poligono circoscrivibile a un cerchio il � = b
3
cui centro coincide con il piede dellaltezza.
Data una retta a, detta asse di rotazione, il
luogo delle rette parallele ad a e da essa S = 2 π r ⋅ h
equidistanti si chiama superficie cilindrica l
S = 2 π r ⋅ h + 2 π r2
circolare; ciascuna delle rette parallele t
2
prende il nome di generatrice e la distanza � = π r ⋅ h
di tali rette dallasse è il raggio.
a
Cono
Si chiama prisma la regione di spazio delimitata dai due poligoni ABCD ... e A′B′C′D′...,
detti basi, e dai parallelogrammi ABB ′A′, Sl = 2 p ⋅ h
BCC′B′, ... detti facce laterali.
St = Sl + 2 Sb
Un prisma si dice retto se il vettore v è per- � = S ⋅ h
b
pendicolare al piano α, regolare se le basi
sono poligoni regolari.
Si chiama cubo un parallelepipedo rettanSl = 4 a2
golo che ha gli spigoli uguali.
St = 6 a2
� = a3
d = a 3
G
E
c
C
Formule
A
Fissata una semiretta a di origine V, si chia- a = h 2 + r 2
ma superficie conica circolare di asse a e
semiapertura α (angolo acuto) il luogo delle Sl = π r ⋅ h
semirette uscenti da V che formano con a St = π r ⋅ h + π r 2
un angolo α.
πr 2 ⋅ h
�=
3
Si definisce superficie sferica di centro O e
raggio r il luogo dei punti dello spazio che St = 4 π r 2
hanno distanza da O uguale a r.
� = 4 πr 3
3
73
Triangoli rettangoli
Obiettivo
6
Applicare i teoremi studiati a problemi di geometria solida
PROBLEMI SVOLTI PER PUNTI (DA COMPLETARE ALGEBRICAMENTE)
42. È data una piramide retta a base quadrata ABCD di lato 8 cm e spigolo laterale 12 cm. Determinare:
�
a. le funzioni goniometriche degli angoli VBO e VBA, essendo V il vertice e O il centro di base;
b. quale angolo è maggiore;
c. il volume e larea della superficie totale della piramide.
V
Risoluzione per punti
Il triangolo VBO è rettangolo in O. Applicare il teorema dei trian = BO .
goli per calcolare cosVBO
VB
Sia H il punto medio di AB. Si osservi che il triangolo VHB è ret = HB .
tangolo in H; calcolare cosVBA
VB
Confrontare i valori ottenuti.
Determinare laltezza della piramide. Calcolare il volume. Determinare laltezza VH della faccia laterale. Calcolare larea della superficie totale.
C
D
O
B
A
43. È data una piramide retta a base triangolare equilatera ABC di lato AB = 6 cm e spigolo AV = 4 cm.
�
Determinare:
a. le funzioni goniometriche dellangolo VAO, essendo O il centro di base;
b. il valore dellangolo VAO;
c. il volume della piramide.
Risoluzione per punti
Osservare che in un triangolo equilatero si ha AO = 2 h, essen3
do h laltezza del triangolo equilatero. Osservare che il triangolo
VAO è rettangolo in O, calcolare VO. Applicare il teorema dei
triangoli per sen VAO = VO .
AV
Dedurre il valore dellangolo VAO.
Calcolare il volume.
V
C
O
A
B
44. È dato un parallelepipedo di dimensioni AB = 10 cm, BF = 3 cm, FG = 4 cm.
Sia AG la diagonale del parallelepipedo.
a. Risolvere il triangolo ABG.
b. Determinare laltezza relativa alla base AG.
c. Calcolare il volume di un cubo di lato pari a BK.
�
Risoluzione per punti
Il triangolo ABG è rettangolo in B. Calcolare il valore di BG e di
AG. Applicare il teorema dei triangoli per sen AGB.
Applicare il teorema dei triangoli al triangolo BGK per determinare BK.
Calcolare il volume del cubo.
74
G
H
K
F
E
D
C
A
B
Triangoli rettangoli
45. In una semisfera è inscritta una piramide avente per base un triangolo equilatero ABC inscritto nel
�
cerchio massimo.
= − 7 , essendo O il cenSi ha che AV = 16 cm, essendo V il vertice della piramide, e cosVOA
25
tro di base.
Determinare il volume della piramide.
Risoluzione per punti
Osservare la figura sezione ottenuta con un piano ortogonale
alla base e passante per il vertice. Determinare, a partire da
= − 7 , le funzioni goniometriche dellangolo alla
cosVOA
25
circonferenza VEA che insiste sulla corda AV. Applicare il
teorema della corda per determinare il raggio della sfera.
Determinare il lato del triangolo equilatero applicando il teorema della corda e quindi larea del triangolo di base.
Osservare che il triangolo VAE è rettangolo. Applicare il teorema dei triangoli al triangolo rettangolo VAH, essendo H il
piede dellaltezza della piramide.
Calcolare il volume della piramide.
V
A
C
O
B
46. Determinare il volume del solido ottenuto dalla rotazione completa del triangolo scaleno ABC; attorno al lato BC, sapendo che larea del triangolo è
= 7 .
S = 7 cm2, AB = 5 cm e che sen ABC
25
C
�
Risoluzione per punti
Applicare il teorema dellarea per determinare CB.
Applicare il teorema dei triangoli al triangolo rettangolo ABH, essendo H il
piede dellaltezza condotta da A a BC. Determinare la misura del raggio r = AH.
Il solido ottenuto è un solido composto da due coni di base coincidente. Calcolare il volume del solido di rotazione.
E
H
A
H
B
75
Triangoli rettangoli
Obiettivo
7
Applicare i teoremi studiati a problemi con grafici, ricerca
di massimo e minimo, discussione
PROBLEMI SVOLTI PER PUNTI (DA COMPLETARE ALGEBRICAMENTE)
47. Sia P un punto dellarco del quadrante AOB di centro O e raggio r, M il punto medio del raggio
�
OA e N il punto sul raggio OB per cui si ha ON = 3 r. Studiare in funzione di x = POM larea
2
del quadrilatero OMPN. Determinare per quale valore di x tale area è massima.
Risoluzione per punti
Posto x = POM, imporre le limitazioni su x. Studiare i casi limite.
Applicare il teorema dellarea ai triangoli OMP e ONP.
� (OMPN )
.
Per facilitarsi, tracciare il grafico della funzione f ( x ) =
r2
Determinare il massimo di f(x).
48. Sulla semicirconferenza di centro O e diametro AB = 2 r, determinare un punto P tale che, detta H
la sua proiezione sul diametro AB, si abbia:
a. 2AH + PH = 3 r;
b. 2AH + PH = k r.
�
Risoluzione per punti
Posto x = PAB, imporre le limitazioni su x. Studiare geometricamente i casi limite.
Applicare il teorema dei triangoli rettangoli ad ABP e APH e determinare AH, PH.
Risolvere lequazione 2AH + PH = 3 r.
Discutere lequazione parametrica 2AH + PH = k r.
49. Sulla semicirconferenza di centro O e diametro AB = 2 r, si conduce la corda AC. Indicate con H
la proiezione di C sul diametro AB e con K la proiezione di C sulla tangente alla circonferenza condotta da B, studiare in funzione di x = CAB il perimetro del rettangolo HBKC. Determinare per
quale valore di x tale perimetro è massimo.
�
Risoluzione per punti
Posto x = CAB, imporre le limitazioni su x. Studiare i casi limite.
Applicare il teorema della corda per determinare CB e dei triangoli rettangoli a CHB per determinare CH, HB.
Calcolare il perimetro 2p = 2(CH + HB).
2p
Per facilitarsi, studiare la funzione f ( x ) =
e tracciarne il grar
fico.
Determinare il massimo di f(x).
76
C
A
O
H
K
B
Triangoli rettangoli
attività di sportello
tempo previsto: 1 ora e 30 minuti
Obiettivi
Obiettivo 1:
risoluzione dei triangoli
rettangoli
Punti
1. Denotando con a la misura dellipotenusa, con b e c le misure dei cateti, con β e γ le ampiezze degli angoli opposti a b e c, risolvere il
triangolo rettangolo per cui si ha:
a = 40
sen γ =
3
4
/
Obiettivo 2:
risoluzione di semplici problemi
sui triangoli rettangoli
2. Determinare larea e il perimetro di un triangolo rettangolo sapendo
che laltezza relativa allipotenusa è lunga 10 cm e che un cateto forma con lipotenusa un angolo di coseno pari a 5 .
4
/
Obiettivo 3:
calcolare larea di un triangolo
3. Determinare larea di un triangolo, sapendo che le misure di due suoi
lati consecutivi sono 3 e 10 cm e che langolo tra essi compreso ha
tangente uguale a 12 .
5
/
Obiettivo 4:
applicare il teorema
della corda
4. Determinare il raggio della circonferenza circoscritta al triangolo ABC,
= 24 .
sapendo che AB = 21 cm e cos ACB
25
/
Obiettivo 5:
applicare i teoremi studiati
a problemi di geometria piana
5. Determinare larea e il perimetro del triangolo isoscele acutangolo
8
5 cm e raggio della circonferenza circoABC che ha base AB =
9
/
scritta ad esso r = 1 cm.
77
Triangoli rettangoli
Verifica conclusiva
tempo previsto: 2 ore
Argomenti
Quesiti
Risoluzione
poligono
1a Dato il triangolo equilatero ABC, di lato l, condurre per A,
Discussione
Risoluzione
poligono
Applicazione
alla geometria
dello spazio
esternamente al triangolo, una retta r tale che, indicate
con H e K le proiezioni di B e C su r e posto CAK = x,
3 l.
si abbia BH + CK =
2
1b Generalizzare la relazione precedente e studiare BH + CK = kl.
Punti
/
/
2 Considerare sul prolungamento del lato AD, dalla parte di D,
1
del quadrato ABCD di lato l, un punto P tale che cos PBA = .
3
Sia T il punto di intersezione del segmento PB con il lato CD.
Calcolare larea e il perimetro del quadrilatero ABTD.
/
3a Il rettangolo ABCD è tale che la retta che congiunge i punti
medi dei lati più lunghi, AB = CD = a, lo divide in due rettangoli
simili a quello dato.
Determinare la lunghezza dei lati minori del rettangolo.
/
3b Sulla retta condotta perpendicolarmente al piano del rettangolo
nel punto medio del lato AD, prendere un punto V in modo che
il piano dei punti V, B, C formi con il piano del rettangolo dato
un angolo di coseno 2 . Calcolare il volume della piramide
13
di vertice V e base ABCD.
78
/
Triangoli qualunque
Teoria in sintesi
Teoremi sui triangoli
Teorema dei seni
In un triangolo le misure dei lati sono
proporzionali ai seni degli angoli opposti.
C
γ
a
b
β
α
A
a = b = c
sen α
sen β
sen γ
c
B
In un triangolo il rapporto tra le misure di
due lati è uguale al rapporto tra i seni degli
angoli a essi opposti:
a = sen α
b
sen β
Teorema delle proiezioni
In un triangolo qualunque la misura di un lato
è uguale alla somma dei prodotti delle misure
degli altri due lati per il coseno dellangolo
che ciascuno di questi forma con il primo.
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Teorema del coseno o di Carnot
In un triangolo il quadrato della misura di un
lato è uguale alla somma dei quadrati delle
misure degli altri due, diminuita del doppio
prodotto delle misure di questi due lati per il
coseno dellangolo da essi compreso.
a 2 = b 2 + c 2 − 2 b c cos α
b 2 = a 2 + c 2 − 2 a c cos β
c 2 = a 2 + b 2 − 2 a b cos γ
79
Triangoli qualunque
Obiettivo
1
Applicare il teorema dei seni
sercizio risolto
Determinare gli elementi incogniti del triangolo ABC, essendo α, β, γ le ampiezze rispettive degli angoli di vertici
A, B, C, sapendo che:
C
γ
AB = 7
3
cos α =
5
π
β =
3
α
A
β
B
Si ricava sen α = 4 .
5
Si ricava γ = π − (α + β).
Si determina
3 −3 + 4 3
cos γ = cos ( π − (α + β) ) = − cos(α + β) = − cos α cos β + sen α seenβ = − 3 ⋅ 1 + 4 ⋅
=
.
5 2 5 2
10
Si determina
3 4+3 3
sen γ = sen ( π − (α + β) ) = sen (α + β) = sen α cos β + cos α sen β = 4 ⋅ 1 + 3 ⋅
=
.
5 2 5 2
10
3 315 − 140 3
AB sen β =
7
⋅
=
.
Si applica il teorema dei seni per determinare AC =
sen γ
11
4+3 3 2
10
− 224 + 168 3
AB sen α =
7
⋅4 =
.
Si applica il teorema dei seni per determinare BC =
sen γ
11
4+3 3 5
10
1. Determinare gli elementi incogniti del triangolo ABC, essendo α, β, γ le ampiezze rispettive
�
degli angoli di vertici A, B, C, sapendo che: AB = 2, cos α = 4 , β = π .
5
3
2. Determinare le funzioni goniometriche dellangolo α del triangolo acutangolo ABC, essendo α,
β, γ le ampiezze rispettive degli angoli di vertici A, B, C, sapendo che: AB = 4, AC = 3, β = π .
6
�
3. Determinare gli elementi incogniti del triangolo ABC, essendo α, β, γ le ampiezze rispettive
degli angoli di vertici A, B, C, sapendo che: AC = 3 2 , α = π , β = 2 π.
4
3
�
4. Determinare gli elementi incogniti del triangolo ABC, essendo α, β, γ le ampiezze rispettive
�
degli angoli di vertici A, B, C, sapendo che: BC = 1 + 3 , β = π , γ = π .
3
3
4
5. Determinare gli elementi incogniti del triangolo ottusangolo ABC, essendo α, β, γ le ampiez�
ze rispettive degli angoli di vertici A, B, C, sapendo che: BC = 2, AC = 2 3 , α = π .
6
80
Triangoli qualunque
Obiettivo
2
Applicare il teorema del coseno
sercizio risolto
Determinare la lunghezza del lato BC e il seno degli angoli β e γ e del triangolo ABC, essendo
α, β, γ le ampiezze rispettive degli angoli di vertici A, B, C, sapendo che:
AB = 3
C
AC = 2
α = π
3
γ
β
α
A
B
Si applica il teorema del coseno per determinare:
BC = AB + AC − 2 AB ⋅ AC ⋅ cos α = 9 + 4 − 2 ⋅ 2 ⋅ 3 ⋅ 1 = 7 ⇒ BC = 7 .
2
2
2
Si applica il teorema dei seni per determinare senβ =
3
2 = 21 .
7
2 7
Si applica il teorema dei seni per determinare sen γ =
3 3 3 21
=
.
14
2 7
Alcuni consigli utili
Negli esercizi proposti di seguito potrà capitare di dover calcolare funzioni goniometriche di angoli meno
noti, ad esempio: π , 7 π.
12 12
In tal caso si ricorre alle formule di bisezione, ottenendo:
sen π =
12
1 − cos π
6 =
2
1−
2
3
2 =
2− 3 =
4
6 −
4
2
Analogamente per gli altri casi.
6. Determinare BC e sen β del triangolo ABC, essendo α, β, γ le ampiezze rispettive degli angoli
�
di vertici A, B, C, sapendo che: AB = 10, AC = 2 2 , α = π .
4
7. Determinare BC e β del triangolo acutangolo ABC, essendo α, β, γ le ampiezze rispettive degli
angoli di vertici A, B, C, sapendo che: AB = 3, AC = 3 , α = π .
2
3
�
81
© RCS Libri S.p.A. - Divisione Education, Milano
2
Triangoli qualunque
8. Tenendo conto delle tabelle relative agli angoli, determinare AB, α e β del triangolo ABC, es�
sendo α, β, γ le ampiezze rispettive degli angoli di vertici A, B, C, sapendo che:
BC =
6 +
2 , AC =
6 −
2, γ = π .
3
9. Determinare AC, α e γ del triangolo ABC, essendo α, β, γ le ampiezze rispettive degli angoli
di vertici A, B, C, sapendo che:
AB = 12, BC = 6 2 , β = 7 π.
12
�
10. Determinare cos β del triangolo ABC, essendo α, β, γ le ampiezze rispettive degli angoli di
vertici A, B, C, sapendo che:
�
AB = 2, AC = 7, BC = 6.
Obiettivo
3
Risolvere problemi di geometria piana
tramite i teoremi sui triangoli qualunque
PROBLEMI SVOLTI PER PUNTI (DA COMPLETARE ALGEBRICAMENTE)
= π . Determinare perimetro e area del
11. Sia ABC un triangolo tale che AB = 2, AC = 1 e che BAC
6
�
quadrato costruito sul lato BC.
Risoluzione per punti
Determinare BC tramite il teorema del coseno applicato al triangolo ABC.
Calcolare il perimetro e larea del quadrato di lato BC.
= π . Sia r la retta
12. Sia ABC un triangolo isoscele di base BC, e tale che AB = AC = 1 e che BAC
6
perpendicolare ad AB condotta da A, e D il punto in cui tale retta interseca la semiretta condot = π . Determinare il
ta da C esternamente al triangolo ABC e formante con AC un angolo ACD
4
perimetro del quadrilatero ABCD.
�
Risoluzione per punti
Determinare gli angoli CÂD e A DC.
Determinare AD tramite il teorema dei seni applicato al triangolo ACD.
Determinare CD tramite il teorema dei seni applicato al triangolo ACD.
Determinare BC tramite il teorema sui triangoli rettangoli (triangolo BAH dove AH è laltezza su BC),
oppure tramite il teorema del coseno applicato al triangolo ABC.
Calcolare il perimetro del quadrilatero ABCD come somma di AB, BC, CD, AD.
82
Triangoli qualunque
13. In una partita di baseball lesterno destro (A) lancia la palla in prima base (B) e la prima base lan�
7 π,
cia la palla al ricevitore (C). Sapendo che AB = 41 m, BC = 27 m e che ABC = 105° =
12
determinare quanto avrebbe percorso in meno la palla se lesterno destro (A) lavesse lanciata
direttamente al ricevitore (C). Usare la calcolatrice scientifica approssimando il risultato a meno
di 1 .
10
Esterno centro
Esterno destro
Esterno sinistro
A
Campo esterno
Interbase
Terza base
41 m
Seconda base
Diamante
Lanciatore
B
18,44 m
Prima base
Battitore
Ricevitore
C
27 m
Risoluzione per punti
Determinare AC tramite il teorema del coseno applicato al triangolo ABC.
Calcolare la differenza tra la somma AB + BC e AC.
= π . Determinare il perimetro del
14. Sia ABC un triangolo rettangolo in C tale che AB = 4 e ABC
6
triangolo ABD, dove D è il punto di intersezione del segmento BC con la semiretta condotta da A
= π.
e formante con AB un angolo BAD
4
�
Risoluzione per punti
Determinare BD tramite il teorema dei seni applicato al triangolo BDA.
Determinare AD tramite il teorema dei seni applicato al triangolo BDA.
Calcolare il perimetro del triangolo ABD come somma di AB, BD, AD.
83
Triangoli qualunque
Teoria in sintesi
Ulteriori teoremi sui triangoli
Formule di Briggs
In un triangolo le funzioni
goniometriche degli angoli
si possono ottenere dalle
misure dei lati a, b, c
e dal semiperimetro p:
sen α =
2
( p − b) ( p − c)
bc
cos α =
2
p ( p − a)
bc
sen
β
=
2
( p − a) ( p − c)
ac
cos
β
=
2
p ( p − b)
ac
sen
γ
=
2
( p − a) ( p − b)
ab
cos
γ
=
2
p ( p − c)
ab
C
Formula di Erone
In un triangolo larea è data da:
�=
p ( p − a) ( p − b) ( p − c)
Raggio della circonferenza inscritta nel triangolo
γ
β
r = � = ( p − a ) tg α = ( p − b ) tg = ( p − c ) tg
p
2
2
2
a
β
α
A
84
γ
b
c
B
Raggio della circonferenza
circoscritta al triangolo
R = abc
4�
Triangoli qualunque
Obiettivo
4
Risolvere problemi di geometria solida
tramite i teoremi sui triangoli qualunque
PROBLEMI SVOLTI PER PUNTI (DA COMPLETARE ALGEBRICAMENTE)
15. Un prisma retto ha per base un triangolo acutangolo ABC, tale che AB = a 6 , BC = 2 a e
�
= π . Determinare larea della superficie laterale e il volume, sapendo che laltezza del priBAC
4
sma è 2 a 3 .
Risoluzione per punti
tramite il teorema dei seni applicato al triangolo ABC.
Determinare sen ACB
Determinare AC tramite il teorema dei seni applicato al triangolo ABC.
Calcolare il perimetro del triangolo ABC.
Calcolare larea della superficie laterale del prisma.
Calcolare larea di base applicando la formula dellarea.
Calcolare il volume del prisma.
16. Una piramide retta, di vertice V, ha per base il triangolo ABC, rettangolo in A, la cui area è 24 a 2,
�
dove a è una lunghezza assegnata. Si sa inoltre che AB = 3 e che il piano della faccia VAB della
BC 5
piramide forma col piano della base ABC un angolo γ tale che sen γ = 12 .
13
a. Calcolare laltezza della piramide.
b. Verificato che essa è VO = 24 a, calcolare la distanza del vertice C dal piano della faccia VAB.
5
(Esame di Stato sessione suppletiva 2001)
Risoluzione per punti
Determinare AB, AC, BC tramite il teorema dei triangoli rettangoli e il teorema dellarea applicati al
triangolo ABC.
Ricordare che in una piramide retta il piede dellaltezza cade nel centro della circonferenza inscritta
nel triangolo di base. Determinare il raggio di tale circonferenza r = A .
p
Determinare laltezza della piramide VO tramite il teorema dei triangoli rettangoli applicato al triangolo VOT, essendo T il punto di tangenza della circonferenza inscritta con il lato AB.
Calcolare la distanza del vertice C dal piano della faccia VAB, ad esempio utilizzando la formula
3V .
inversa del volume: CK =
A( ABV )
85
Triangoli qualunque
Obiettivo
5
Applicare i teoremi studiati a problemi
con studio di funzione
PROBLEMI SVOLTI PER PUNTI (DA COMPLETARE ALGEBRICAMENTE)
17. In un quadrato ABCD avente un lato AB di lunghezza AB = 2, considerare sulla diagonale BD
2
2
�
un punto P in modo da determinare, posto x = BÂP, la funzione f ( x ) = BP + AP .
a. Studiare i casi limite.
b. Calcolare in particolare il valore assunto dalla funzione per x = π .
6
Risoluzione per punti
= sen π − x + π = sen x + π .
Determinare sen APB
4
4
Determinare BP tramite il teorema dei seni.
Determinare AC tramite il teorema dei seni.
Studiare i casi limite P ≡ B, P ≡ D e determinare i corrispondenti valori di f (x).
2
2
Determinare f ( x ) = BP + AP .
Determinare f π .
6
= π,
18. Dopo aver determinato gli elementi incogniti del triangolo ABC, in cui AB = 5, ACB
6
= − 3 , calcolare larea. Condotta la semiretta che da C incontri il segmento AB nel punctg BAC
4
1
1
determinare la funzione f ( x ) =
to H, posto x = ACH,
AH +
CH . Calco20 3 − 15
16 3 − 12
lare il valore assunto dalla funzione nei casi limite. Giustificare la monotonia della funzione f (x)
entro lintervallo di variabilità dellincognita.
�
Risoluzione per punti
e cos BAC
, nota ctg BAC
= −3.
Determinare sen BAC
4
+ π = sen BAC
+ π.
= sen π − BAC
Determinare sen ABC
6
6
Determinare BC tramite il teorema dei seni.
Determinare AC tramite il teorema dei seni.
Calcolare larea del triangolo.
Studiare i casi limite H ≡ A, H ≡ B e determinare i corrispondenti valori di f (x).
Determinare AH tramite il teorema dei seni.
Determinare CH tramite il teorema dei seni.
1
1
Determinare f ( x ) =
AH +
CH .
20 3 − 15
16 3 − 12
Giustificare la monotonia della funzione f(x) nellintervallo di variabilità dellincognita tramite considerazioni geometriche.
86
Triangoli qualunque
attività di sportello
tempo previsto: 1 ora e 30 minuti
Obiettivi
Punti
1. Determinare gli elementi incogniti del triangolo ABC, essendo α, β, γ
le ampiezze rispettive degli angoli di vertici A, B, C, sapendo che:
Obiettivo 1:
applicare il teorema dei seni
Obiettivo 2:
applicare il teorema del coseno
BC = 4
π
β =
6
7
π
γ =
12
γ
A
α
β
B
/
2. Determinare gli elementi incogniti del triangolo ABC, essendo α, β, γ
le ampiezze rispettive degli angoli di vertici A, B, C, sapendo che:
BC = 2 2
AC = 2 3
π
β =
3
Obiettivo 3:
risolvere problemi di geometria
piana tramite i teoremi
sui triangoli qualunque
C
/
3. Sia ABC un triangolo equilatero di lato 3 cm, D il punto su AC tale
che CD = 1 cm ed E il punto medio di AB. Determinare il perimetro e
larea del triangolo BDE. Determinare inoltre il raggio della circonferenza circoscritta al triangolo BDE.
/
87
Triangoli qualunque
Verifica conclusiva
tempo previsto: 2 ore
Argomenti
Quesiti
Risoluzione
di triangoli
1a Il triangolo ABC ha la base AB = 8 cm.
Applicazione
alla geometria
solida
Applicazione
allo studio
di funzioni
Punti
Inoltre, cos α = 11 e cos β = 7 .
16
8
Stabilire se il triangolo è ottusangolo.
/
1b Calcolare larea e il perimetro del triangolo.
/
1c Determinare la lunghezza delle mediane del triangolo.
/
2 Il triangolo ABC ha il lato AC = 10 cm.
Inoltre, cos α = 1 e tg β = 3 .
2
4
Calcolare larea della superficie totale del solido generato dalla
rotazione completa di ABC intorno ad AB.
/
3a Il triangolo isoscele acutangolo ABC ha la base AB = 6 e
sen γ = 24 . Risolvere il triangolo.
25
/
3b Sia P un punto del lato AC, M il punto medio di AB e sia PC = x.
2
Determinare la funzione f ( x ) =
Studiare i casi limite.
2
2
PB + PM + MB
.
4
/
3c Determinare il valore di x per cui la funzione assume
valore minimo.
88
/










