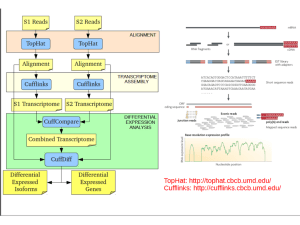
U"lizzo • Assemblaggio ex novo di genomi – Ancora molto difficile per grandi genomi • Iden"ficazione di nuovi trascri;omi – Difficile se completamente nuovi • Confronto tra trascri;omi – Molto u"lizzato sia per classificazione che per iden"ficazione di cause di patologie • Iden"ficazioni di varian" in genomi – Molto u"lizzato per individuare polimorfismi e mutazioni patologiche Altre applicazioni • ChipSeq per iden"ficare regioni del genoma a cui specifiche proteine si legano • miRSeq per iden"ficare microRNA • ... Confronto tra trascri;omi (RNASeq) Campione 1 Sequenziamento Allineamento al genoma ed iden"ficazione di giunzioni esoni introni Assemblaggio dei trascriI Trascri;oma Campione 2 Sequenziamento Allineamento al genoma ed iden"ficazione di giunzioni esoni introni Assemblaggio dei trascriI Trascri;oma Trascri;oma “unione” Iden"ficazione delle differenze sia qualita"ve che quan"ta"ve Le “reads” vanno assegnate alle giunzioni introne Allineamento al genoma ed iden"ficazione di giunzioni esoni introni esone Allineamento di RNASeq Nuovi trascriI reads TrascriI no" Abbondanza rela"va delle isoforme? genoma Quan"ficazione Abbondanza rela"va delle isoforme FPKM: Frammen" per kilobase per esone per milione di frammen" Fold change: log2 del rapporto tra le FPKM di due geni/esoni Confronto tra campioni Campione 1 Campione 2 TrascriI up-­‐regola" 377 1442 TrascriI down-­‐regola" 802 1036 Cosa ci dicono i trascriI differenzialmente espressi sul processo biologico? Occorre analizzarne la funzione • h;p://www.ncbi.nlm.nih.gov/pmc/ar"cles/
PMC2949280/ • h;p://www.mi.fu-­‐berlin.de/wiki/pub/ABI/
GenomicsLecture13Materials/rnaseq2.pdf Banche da" u"li • Gene Ontology – Assegna ad ogni gene la sua • Funzione molecolare • Processo biologico • Componente cellulare • KEGG (pathways) • Interpro (famiglie) Calcolare la significa"vità • Distribuzione ipergeometrica – Una distribuzione che descrive la probabilità di trovare k even" in n estrazioni da una popolazione finita di N casi che con"ene esa;amente K even" • Si usa per valutare se una certa so;o popolazione e’ so;o o sopra rappresentata in un campione Esempio Estra0e Non estra0e Totale Palline rosse 4 1 5 Palline verdi 6 39 45 Totale 10 40 50 Arricchimento funzionale dei geni up-­‐ down – regola": Arricchimento funzionale dei geni up-­‐ down – regola": ChipSeq Cross-­‐link chimico e frazionamento Y Y DNA legato a proteine per esempio regolatrici Sequenziamento Purificazione Selezione con an"corpo Iden"ficazione picchi ACGTGACAGGTACACCCTA ... ... ... Mappare sul genoma Iden"ficare “mo"vi” comuni • h;p://www.slideshare.net/ajene/20091110-­‐
technical-­‐seminar-­‐chipseq-­‐data-­‐analysis?
related=1 • h;p://www.mi.fu-­‐berlin.de/wiki/pub/ABI/
GenomicsLecture14Materials/chipseq.pdf • Una volta sequenziato un genoma, occorre iden"ficare i geni e cercare di assegnare loro una funzione. Il modello biologico: procario" Iden"ficazione di mo"vi specifici (per es. promotori e TATA box) Lunghezza dell’open reading frame (1 codone di inizio ATG e 3 codoni di STOP) Uso codoni Periodicità e proprietà sta"s"che Al ribosoma: Lunghezza dell’ORF • Cerca puta"vi codoni di inizio (ATG) • Leggi le triple;e fino ad incontrare un segnale di STOP • Ce ne aspeIamo casualmente uno ogni circa 20 codoni. • Possiamo quindi calcolare la probabilità che una sequenza senza terminatori esista per caso (possiamo tener conto della composizione del genoma) Il modello biologico: eucario" Struttura di un gene eucariota
promotore 5’ Esone Introne Esone AUG gt Fa;ori di trascrizione AUG gt ag ag Introne gt gt ag ag 3’ Esone DNA ag Trascri;o primario TER Sito di taglio Segnale per il polyA CAP AUG 5’UTR AAA-­‐AAA mRNA TER 3’UTR proteina Le regioni nei riquadri contengono segnali in termini delle loro sequenze Per approfondire • h;p://faculty.ksu.edu.sa/77379/Documents/
BCH451(2)32-­‐33.pdf Ricerca di geni • Ricerca di segnali di sequenza (mo"vi) • Modelli sta"s"ci del gene (per esempio HMM) • Similarità con geni no" nello stesso o in altri organismi Ricerca di geni • Ricerca di segnali di sequenza (mo"vi) • Modelli sta"s"ci del gene (per esempio HMM) • Similarità’ con geni no" nello stesso o in altri organismi Matrici posizione specifiche Supponiamo di conoscere le sequenze di varie istanze di una regione possiamo allinearle e iden"ficare le loro cara;eris"che di sequenza CTTGGTGACGTG!
TAGGATGAGTCG!
A TACGTAGAGTCG!
TAGGATTTATCG!
T TAGCGCGAGTCG! Conteggi C TAATCGCTACAG!
G ...!
1 2 3 4 5 6 7 8 9 10 11 12 0 6 0 0 2 1 0 4 2 0 1 0 6 1 1 1 1 3 1 2 0 4 1 0 1 0 1 1 1 1 1 0 1 1 4 0 0 0 3 4 2 1 4 0 3 2 0 7 Frequenze 1 2 3 4 5 A 0 .86 0 0 .29 .14 0 T .85 .14 .14 .14 .14 .43 .14 .29 0 C .14 0 .14 .14 .14 .14 .14 0 .14 .14 .57 0 G 0 .43 .57 .29 .14 .57 0 .43 .29 0 0 6 7 8 9 10 11 12 .57 .29 0 .14 0 .57 .14 0 1 Matrici posizione specifiche 1 2 3 4 5 A 0 .86 0 0 .29 .14 0 T .85 .14 .14 .14 .14 .43 .14 .29 0 C .14 0 .14 .14 .14 .14 .14 0 .14 .14 .57 0 G 0 .43 .57 .29 .14 .57 0 .43 .29 0 0 6 7 8 9 10 11 12 .57 .29 0 .14 0 .57 .14 0 1 Se il numero di casi è sufficientemente alto. le frequenze possono approssimare le probabilità. però dobbiamo tener conto in qualche modo del campionamento incompleto Non possiamo assumere che non troveremo mai una sequenza che appar"ene alla classe che s"amo analizzando con una C in dodicesima posizione Si u"lizza il metodo degli pseudocount. Uno pseduocount è un valore (non necessariamente intero) che si aggiunge al numero di casi osserva" per modificare la probabilità a;esa in un modello. Per esempio possiamo aggiungere 1 oppure 1/N dove N è il numero di casi. Matrici posizione specifiche 1 2 3 4 5 6 7 8 9 10 11 12 A 0 6 0 0 2 1 0 4 2 0 1 0 T 6 1 1 1 1 3 1 2 0 4 1 0 C 1 0 1 1 1 1 1 0 1 1 4 0 G 0 0 3 4 2 1 4 0 3 2 0 7 1 2 3 4 5 6 7 8 9 10 11 12 A 1 7 1 1 3 2 1 5 3 1 2 1 T 7 2 2 2 2 4 2 3 1 5 2 1 C 2 1 2 2 3 2 2 1 2 2 5 1 G 1 1 4 5 3 4 3 1 8 1 2 3 4 5 6 7 8 9 10 11 Conteggi con pseudocounts Frequenze 2 5 1 12 A .09 .64 .09 .09 .27 .18 .09 .45 .27 .09 .18 .18 T .64 .18 .18 .18 .18 .36 .18 .27 .09 .45 .18 .18 C .18 .09 .18 .18 .18 .18 .18 .09 .18 .18 .45 .18 G .09 .09 .36 .45 .27 .18 .45 .09 .36 .27 0.9 .73 Frequenze≅ Probabilità Per rendere i valori addi"vi usiamo i logaritmi 1 2 3 4 5 6 7 8 9 10 11 12 A .09 .64 .09 .09 .27 .18 .09 .45 .27 .09 .18 .18 T .64 .18 .18 .18 .18 .36 .18 .27 .09 .45 .18 .18 C .18 .09 .18 .18 .18 .18 .18 .09 .18 .18 .45 .18 G .09 .09 .36 .45 .27 .18 .45 .09 .36 .27 0.9 .73 1 2 3 4 5 6 7 8 9 10 11 12 A -­‐2.5 -­‐0.7 -­‐3.5 -­‐3.5 -­‐1.9 -­‐2.5 -­‐3.5 -­‐1.1 -­‐1.9 -­‐3.5 -­‐2.5 -­‐2.5 T -­‐0.7 -­‐2.5 -­‐2.5 -­‐2.5 -­‐2.5 -­‐1.5 -­‐2.5 -­‐1.9 -­‐3.5 -­‐1.1 -­‐2.5 -­‐2.5 C -­‐2.5 -­‐3.5 -­‐2.5 -­‐2.5 -­‐2.5 -­‐2.5 -­‐2.5 -­‐3.5 -­‐2.5 -­‐2.5 -­‐1.1 -­‐2.5 G -­‐2.5 -­‐2.5 -­‐1.5 -­‐1.1 -­‐1.9 -­‐2.5 -­‐1.1 -­‐3.5 -­‐1.5 -­‐1.9 -­‐3.5 -­‐0.5 Finestra scorrevole lunga k 1 N k p[j=(k+1/2)] p(j+1) p(j+2) p(j+3) p(j+4) p posizione Soglia derivata da una distribuzione casuale. per esempio costruendo varie sequenze casuali con la stessa composizione di quella reale. Distribuzione casuale • Nel caso più semplice f(A) = f(C) = f(G) = f(T) = 0,25 • Possiamo anche tener conto della frequenza osservata delle basi o delle triple;e nel genoma di interesse (o nel gene se ci interessa analizzare le sue regioni) Per approfondire • h;p://bioinforma"ca.upf.edu/T13/
MakeProfile.html • h;p://www.biomedcentral.com/
1471-­‐2105/15/100 Entropia di Shannon Per la base a in posizione i con frequenza rela"va fa.i: H i = −∑ fa,i × log 2 fa,i
Contenuto di informazione R(i) della posizione i: Ri = 2 − (H i + en )
Dove en è una correzione per correggere per il campionamento limitato: 1 s −1
en =
ln 2
×
2n
Entropia di Shannon Immaginiamo un circuito digitale semplice che ha un input a 2 bit (X,Y) e un output a 2 bit (X and Y, X or Y). X(0,1) Y(0,1) X and Y Y or Y • Input: (0,0); (1,1); (1,0); (1,1) con p = ¼ – H(X,Y)=4(-­‐1/4log21/4)=2 bit • Output: (0,0);(0,1);(1,1) con p = ¼; ½; ¼; – H(X and Y, X or Y) = 2(-­‐¼log2¼)-­‐½log2½= 1 + ½ = 1.5 bit Il circuito riduce l’”informazione” di mezzo bit, infaI ho meno informazione su X e Y in output di quanta ne avessi in input. Entropia di Shannon 1 Matrice di frequenze 3 4 5 6 7 8 9 10 11 12 A .09 .64 .09 .09 .27 .18 .09 .45 .27 .09 .18 .18 T .64 .18 .18 .18 .18 .36 .18 .27 .09 .45 .18 .18 C .18 .09 .18 .18 .18 .18 .18 .09 .18 .18 .45 .18 G .09 .09 .36 .45 .27 .18 .45 .09 .36 .27 0.9 .73 1 H i = −∑ fa,i × log 2 fa,i
2 3 4 5 6 7 8 9 10 11 12 1.67 1.49 1.61 1.50 1.98 1.92 1.50 1.69 1.65 1.68 2.92 1.00 1 Bits = fa,i × H i
2 2 3 4 5 6 7 8 9 10 11 12 A 0.15 0.95 0.18 0.15 0.54 0.38 0.15 0.84 0.49 0.15 0.58 0.09 T 1.06 0.27 0.36 0.30 0.36 0.77 0.30 0.51 0.16 0.77 0.58 0.09 C 0.30 0.14 0.36 0.30 0.54 0.38 0.30 0.17 0.33 0.31 1.46 0.09 G 0.15 0.14 0.72 0.75 0.54 0.38 0.75 0.17 0.66 0.46 0.29 0.73 • h;p://quantum.phys.cmu.edu/QCQI/
qitd132.pdf • h;p://www.ueltschi.org/teaching/
chapShannon.pdf Sequence logo 1 2 3 4 5 6 7 8 9 10 11 12 A 0.15 0.95 0.18 0.15 0.54 0.38 0.15 0.84 0.49 0.15 0.58 0.09 T 1.06 0.27 0.36 0.30 0.36 0.77 0.30 0.51 0.16 0.77 0.58 0.09 C 0.30 0.14 0.36 0.30 0.54 0.38 0.30 0.17 0.33 0.31 1.46 0.09 G 0.15 0.14 0.72 0.75 0.54 0.38 0.75 0.17 0.66 0.46 0.29 0.73 Come iden"fichiamo le so;o-­‐
sequenze (o mo"vi)? CTTGGTGACGTG!
TAGGATGAGTCG!
TACGTAGAGTCG!
TAGGATTTATCG!
TAGCGCGAGTCG!
TAATCGCTACAG!
...!
• Sperimentalmente (per esempio ChipSeq) • Confrontando regioni specifiche di geni che si comportano allo stesso modo – Gibbs sampling – MEME – ... Sequenze di geni controllate dallo stesso promotore CATCTACATGGACGGTAGACGACGTTGATGGACGTACAGTT...!
GTAGACAACGTTGGCTGCAGATGATGACGTAAATGCACACA...!
CTACACCGTGACACCAGGTACACGCTGAGGCGCAGGACATT...!
Hanno so;osequenze comuni che quindi sono puta"vamente il sito di legame? Sequenze di geni controllate dallo stesso promotore CATCTACATGGACGGTAGACGACGTTGATGGACGTACAGTT...!
GTAGACAACGTTGGCTGCAGATGATGACGTAAATGCACACA...!
CTACACCGTGACACCAGGTACACGCTGAGGCGCAGGACATT...!
Hanno so;osequenze comuni che quindi sono puta"vamente il sito di legame? Se conoscessimo l’allineamento: CATCTACATGGACGGTAGACGACGTTGATGGACGTACAGTT...!
GTAGACAACGTTGGCTGCAGATGATGC...!
CTACACCGTGACACCAGGTACACGCTGAGGCGCAGGACATT...!
1 2 3 4 5 6 A 0.15 0.95 0.18 0.15 0.54 0.38 T 1.06 0.27 0.36 0.30 0.36 0.77 C 0.30 0.14 0.36 0.30 0.54 0.38 G 0.15 0.14 0.72 0.75 0.54 0.38 Se conoscessimo il mo"vo: 1 2 3 4 5 6 A 0.15 0.95 0.18 0.15 0.54 0.38 T 1.06 0.27 0.36 0.30 0.36 0.77 C 0.30 0.14 0.36 0.30 0.54 0.38 G 0.15 0.14 0.72 0.75 0.54 0.38 p posizione ...ACGGTAGACGACGTTGATGGACGT...!
Un possibile metodo: MEME CATCTACATGGACGGTAGACGACGTTGATGGACGTACAGTT...!
GTAGACAACGTTGGCTGCAGATGATGACGTAAATGCACACA...!
CTACACCGTGACACCAGGTACACGCTGAGGCGCAGGACATT...!
Date p sequenze s1...sp, trova le so;o-­‐sequenze più simili, una per ogni sequenza. In altre parole: argmin dist(si , s j )
s1,...,s p i< j
Dove dist(si,sj) è la distanza di Hamming (numero di posizioni in cui i simboli sono diversi tra le due sequenze) ∑
MEME MEME è uno strumento per ricercare motivi (pattern) in un
gruppo di sequenze di acidi nucleici o proteine
MEME rappresenta un motivo come matrici di lettere dipendenti
dalla posizione che descrivono la probabilità di ogni lettera in
ogni posizione (senza gap).
L’input è un insieme di sequenze, l’output una lista di motivi
Usa metodi di modellizzazione statistica per scegliere la
migliore di lunghezza, numero di casi e descrizione.
MEME • Assumiamo che ogni sequenza contenga un solo mo"vo • Il mo"vo è di lunghezza fissa • Se il mo"vo è di lunghezza 3, per esempio, potremmo avere la pi,j: MEME • La matrice per il background può essere per esempio: • La sequenza è vista come una mistura del background e del mo"vo che sono modellate con distribuzioni diverse MEME Definiamo Ztr la probabilità’ che il mo"vo inizi in posizione r della sequenza t Z tr = 1 ∀t
Allora r
Per l’assunzione di un mo"vo per sequenza Esempio per 3 sequenze di lunghezza 5 e un mo"vo di lunghezza 3: Se i si" di inizio sono uniformemente distribui": Dove Lt e’ la lunghezza della sequenza t e W la dimensione del mo"vo ∑
MEME • Data la lunghezza W di un mo"vo e un insieme di sequenze S – Se;a i valori iniziali di p casualmente • S"ma Z da p • S"ma p da Z • Con"nua fino a convergenza MEME Zt1 è la probabilità che il mo"vo inizi da 1: 0.5 * 0.1 * 0.3 *0.25 *0.25 *0.25 *0.25 Zt2= 0.25*0.4*0.1*0.3*0.25*0.25*0.25 ... Normalizza in modo che MEME A T G C A T G C G C A C A G T Per approfondire • h;p://jura.wi.mit.edu/bio/educa"on/
hot_topics/mo"f/mo"f.pdf • h;p://www.sdsc.edu/~tbailey/papers/
meme.ml.pdf Ricerca di geni • Ricerca di segnali di sequenza (mo"vi) • Modelli sta"s"ci del gene o delle regioni che contengono i geni (per esempio HMM) • Similarità’ con geni no" nello stesso o in altri organismi Esempio: isole CpG • Notazione: – C-­‐G – e’ la coppia di basi C-­‐G sulle due eliche complementari del DNA – CpG – e’ il dinucleo"de CG • Processo di me"lazione nel genoma umano – C muta spesso in T, ma questo succede raramente quando la C e’ parte di CpG – Quindi nelle regioni intorno ai promotori di mol" geni I dinucleo"di CpG sono molto piu’ frequen" – Queste regioni sono chiamate isole CpG (di solito lunghe da qualche cen"naio a qualche migliaia di basi) • Problemi: – Data una sequenza, proviene da un’isola CpG? – Come individuo le isole CpG in una sequenza? Una possibilita’: Modelli di Markov Una catena di Markov e’ una triple;a (Q; {p(xi = s)}; A) dove Q e’ un insieme di sta", ogni stato corrisponde a un simbolo in un alfabeto Σ
p(xi) è la probabilità di xi A è la probabilità di transizione: ast= p(xi=t|xi-­‐1=s) Il modello produce in output un insieme di sta" ad ogni istante (osservabili). La probabilità di ogni simbolo xi dipende solo dal valore del simbolo precedente xi-­‐1: p(xi|xi-­‐1…x1) = p(xi|xi-­‐1) La probabilità di una sequenza x di simboli osserva" è: p(x) = p(xL,xL-­‐1,…,x1) = p(xL|xL-­‐1)p(xL-­‐1|xL-­‐2)…p(x2|x1)p(x1) Modello di Markov per discriminare CpG A aAT T aAC aGT C aGC G Le frecce indicano la probabilita’ a che una base preceda o segua l’altra o;enute dalle frequenze osservate in un training set. • Training Set: – Sequenze di DNA che si sa sono isole CpG e sequenze che non lo sono • Dai da" si derivano due modelli di Markov: – ‘+’ model: per le isole CpG – ‘-­‐’ model: per tu;o il resto Modello di Markov per discriminare isole CpG +
• Con"amo il numero di volte c st in cui il simbolo t segue il simbolo s nelle isole CpG +
• Con"amo il numero di volte c
st in cui il simbolo t segue il simbolo s nel resto delle sequenze cst−
• Le frequenze sono quindi: +
cst+
−
a =
ast =
∑
t'
+
cst'
st
∑c
−
t' st'
Possiamo assegnare un punteggio S ad una sequenza x: S(x) = log
P(x|model + )
=
P(x|model − )
∑
a +x i −1 x i
L
log −
i =1
a x i −1 x i
A
C
G
T
A
.180
.274
.426
.120
C
.171
.368
.274
.188
G
.161
.339
.375
.125
T
.079
.355
.384
.182
Data una sequenza, viene da un’isola CpG? P(x|model + )
S(x) = log
=
P(x|model − )
∑
+
a x i −1 x i
L
log −
i =1
a x i −1 x i
Valori di S(x) posi"vi indicano che è più probabile che provenga da un’isola CpG che dal resto delle sequenze e viceversa Come individuo le isole CpG? posizione Frequenza in regioni note Score Posso usare delle finestre scorrevoli. Per esempio, scelta una finestra lunga 101 basi, calcolo il punteggio e lo assegno alla base centrale 10 5 0 Non-­‐CpG CpG islands -­‐0.4 -­‐0.3 -­‐0.2 -­‐0.1 0 0.1 0.2 0.3 0.4 Score Posso u"lizzare gli HMM (Hidden Markov Model) Si tra;a in pra"ca di costruire un modello singolo che tenga conto delle proprietà di entrambe le regioni (isole e no) Posso u"lizzare gli HMM (Hidden Markov Model) Una catena nascosta di Markov e’ una quintuple;a (Q; V; {p(xi = s)}; A; E) dove Q e’ un insieme di sta", ogni stato corrisponde a un simbolo in un alfabeto Σ
V e’ un insieme di simboli osserva" per ogni stato A è la probabilità di transizione: ast= p(xi=t|xi-­‐1=s) E e’ la matrice che con"ene le probabilita’ di emissione: esk ≡ P (vk al tempo t | qt = s) cioè la probabilità che si osservi il simbolo vk al tempo t dato che il valore di q al tempo t è s. Posso u"lizzare gli HMM (Hidden Markov Model) • Posso osservare solo i simboli emessi dal sistema ma
non so quale percorso è stato seguito (per esempio se la
base proviene da un’isola CpG o no)
Due modelli di Markov aAT A T A aGT aAC C ast+
G aGC =
cst+
∑
t'
+
cst'
aAT T aGT aAC C G aGC −
st
a =
−
st
c
∑c
−
t' st'
Due modelli di Markov aAT A+ T+ A-­‐ aGT aAC C+ ast+
G+ aGC =
cst+
∑
t'
+
cst'
aAT T-­‐ aGT aAC C-­‐ G-­‐ aGC −
st
a =
−
st
c
∑c
−
t' st'
Modello nascosto di Markov A+ T+ C+ G+ A-­‐ T-­‐ C-­‐ G-­‐ Ulteriore (cioè le connessioni all’interno dei due set non sono mostrate ma ci sono) set di probabilita’ di transizione da + a -­‐. Ogni stato eme;e un simbolo (che dipende dalle probabilità che abbiamo assegnato alle varie transizioni). Data una sequenza (per esempio CGCG) vorrei sapere qual è la probabilità che sia stata emessa dal modello e da quale stato proviene ciascun simbolo con maggiore probabilità. Per esempio potrebbe essere C+G+C-­‐G-­‐ oppure C+G+C+G-­‐ Il percorso piu’ probabile: • Definizione: – π – sequenza di sta" πj , o percorso • Il percorso piu’ probabile, cioe’ quello a mggiore probabilita’ – π* = argmaxπ P(x. π) su tuI I possibili percorsi π – Puo’ essere trovato u"lizzando una algritmo ricorsivo (per esempio quello di Viterbi) – Qualunque so;o percorso che finisce in un dato punto lungo il vero percorso oImale deve essere esso stesso un percorso oImale fino a quel punto. Quindi il percorso oImale puo’ essere trovato estendendo i so;o percorsi. pl (i + 1) = el , x i+1 max ( pk (i )akl )
k
pk(i) e’ la probabilita’ del percorso piu’ probabile che finisce nello stato k con l’osservazione i Algoritmo: Viterbi • Inizializzazione (i=0): • Ricorsione(i=1…L): p0 (0) = 1, pk (0) = 0 for k > 0
pl (i + 1) = el , xi +1 max ( pk (i )akl )
k
ptri (l ) = arg max k ( pk (i − 1)akl )
• Fine: P ( x,π * ) = max k ( pk ( L)ak 0 )
π *L = arg max k ( pk ( L)ak 0 )
• Traceback (i=L…1): π i*−1 = ptri (π i* )
Esempio: CpG Sequence: CGCG i p
pl (i + 1) = el , xi +1 max ( pk (i )akl )
k
ptri (l ) = arg max k ( pk (i − 1)akl )
pk (i) k pG+ (G) = 1× .13 × .274
+
A+ C+ G+
T+
A+
.180
.274
.426
.120
C+
.171
.368
.274
.188
G+
.161
.339
.375
.125
T+
.079
.355
.384
.182
l pl (i+1) akl i+1 C
G
C
G
β
1
0
0
0
0
A+
0
0
0
0
0
C+
0
.13
0
.012
0
G+
0
0
.034
.036 0
.0032
T+
0
0
0
0
0
A-
0
0
0
0
0
C-
0
.13
0
.0026
0
G-
0
0
.01
0
.00021
T-
0
0
0
0
0
Esempio: CpG Sequenza: CGCG i p
pl (i + 1) = el , xi +1 max ( pk (i )akl )
k
ptri (l ) = arg max k ( pk (i − 1)akl )
pk (i) k pG+ (G) = 1× .13 × .274
+
A+ C+ G+
T+
A+
.180
.274
.426
.120
C+
.171
.368
.274
.188
G+
.161
.339
.375
.125
T+
.079
.355
.384
.182
l pl (i+1) akl i+1 C
G
C
G
β
1
0
0
0
0
A+
0
0
0
0
0
C+
0
.13
0
.012
0
G+
0
0
.034
.036 0
.0032
T+
0
0
0
0
0
A-
0
0
0
0
0
C-
0
.13
0
.0026
0
G-
0
0
.01
0
.00021
T-
0
0
0
0
0
Programmi per la ricerca dei geni basa" su HMM •
•
•
•
•
•
GENSCAN (Burge 1997) FGENESH (Solovyev 1997) HMMgene (Krogh 1997) GENIE (Kulp 1996) GENMARK (Borodovsky & McIninch 1993) VEIL (Henderson. Salzberg. & Fasman 1997) Per approfondire • Dispensa: 6 HMM (presa da Richard Durbin, Sean R. Eddy, Anders Krogh, Graeme Mitchison Biological Sequence Analysis, Cambridge University Press) GenScan States
•
•
•
N -­‐ intergenic region P -­‐ promoter F -­‐ 5’ untranslated region •
Esngl – single exon (intronless) (transla"on start -­‐> stop codon) •
Einit – ini"al exon (transla"on start -­‐> donor splice site) •
Ek – phase k internal exon (acceptor splice site -­‐> donor splice site) •
Eterm – terminal exon (acceptor splice site -­‐> stop codon) •
Ik – phase k intron: 0 – between codons; 1 – a…er the first base of a codon; 2 – a…er the second base of a codon