PROVA SCRITTA DI MECCANICA RAZIONALE (11 giugno 2005

PROVA SCRITTA DI MECCANICA RAZIONALE (11 giugno 2005)
(C.d.L. Ing. Edile - Architettura. Prof. A. Muracchini)
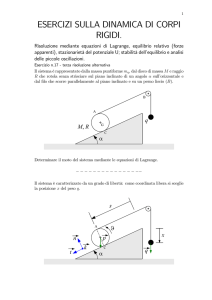
Il sistema rappresentato in figura, mobile in un piano verticale Oxz, è costituito di un disco circolare
pesante omogeneo D (massa m, raggio R) che rotola senza strisciare sulla guida verticale Oz e di un
punto materiale pesante P (massa m) vincolato a muoversi sul semiasse positivo Ox. Il punto P
e il centro G del disco sono collegati da una molla ideale di costante elastica k(> 0) e di lunghezza
a riposo supposta trascurabile. Il punto P è anche soggetto alla forza elastica F = −kAP (k > 0)
essendo A un punto fisso dell’asse Ox tale che | AO |= 2R. Tutti i vincoli sono supposti ideali.
Assunti come parametri lagrangiani xP e zG rappresentati in figura, si chiede:
1) Determinare le configurazioni di equilibrio interne e le eventuali configurazioni di equilibrio di
confine, discutendo la stabilità di quelle interne;
2) Usando le equazioni cardinali della statica, ritrovare le configurazioni di equilibrio (interne) e
determinare le reazioni vincolari che si esercitano nei punti P e C;
3) Ricavare ed integrare le equazioni differenziali del moto sia usando le equazioni cardinali della
dinamica che il metodo lagrangiano;
4) Ricavare eventuali integrali primi del moto.
Supponiamo, ora, che sul punto P agisca anche una forza di attrito coulombiano (coefficiente di attrito
statico fs ). In tali condizioni, si chiede di determinare:
5) Le configurazioni di equilibrio interne del sistema.
D
G
mg
x
x
x
x
x
x
x xP
Ox
x
x
P
x
x
x
x
x
x
zg
x
x
x
x
x
Cx
x
x
x
x
x
x
x
x
x
x
x
x
x
xz
AO =2R
A
x
PROVA SCRITTA DI MECCANICA RAZIONALE (4 luglio 2005)
(C.d.L. Ing. Edile/Architettura - Prof. A. Muracchini)
Il sistema rappresentato in figura, mobile in un piano verticale Oxy, è costituito di un’asta AB pesante
omogenea (massa m, lunghezza 2l) il cui estremo A è vincolato a scorrere, senza attrito, sul semiasse
positivo Oy. Oltre alla forza peso, agiscono sul sistema:
• la forza elastica F = −kOA (k > 0);
• la forza F = F i (F > 0, costante; i versore dell’asse Ox) applicata nel punto B dell’asta.
Assunti come parametri lagrangiani l’angolo θ e l’ordinata q del punto A (vedi figura) si chiede:
1) Determinare le configurazioni di equilibrio interne e le eventuali configurazioni di equilibrio di
confine, discutendo la stabilità di quelle interne;
2) Usando le equazioni cardinali della statica, ritrovare le configurazioni di equilibrio (interne) e
determinare la reazione vincolare che si esercita nel punto A;
3) Ricavare le equazioni differenziali di Lagrange del moto;
4) Ricavare le equazioni cardinali della dinamica e determinare la reazione vincolare che si esercita in
A in condizioni dinamiche.
B
O
F=Fi
i
x
θ
q
A
y
x
PROVA SCRITTA DI MECCANICA RAZIONALE (9 settembre 2005)
(C.d.L. Ing. Edile/Architettura - Prof. A. Muracchini)
Il sistema in figura, mobile nel piano verticale Oxy, è costituito di:
α ) un disco rigido pesante D, omogeneo (massa m, raggio R) vincolato, mediante una cerniera piana,
a ruotare intorno ad un asse fisso orizzontale ad esso ortogonale e passante per un suo punto O posto
a distanza R/2 dal baricentro G;
β ) un punto materiale P (massa m) vincolato a muoversi lungo il diametro AB ortogonale ad OG,
senza uscirne.
Oltre alle forze peso, agisce sul punto P una forza elastica F = kP O(k > 0) (vedi figura).
Supposti i vincoli ideali, scelti i parametri lagrangiani ξ e θ rappresentati in figura e introdotto il
parametro adimensionale λ = kR/mg (∈ <+ ) si chiede:
1) Determinare e discutere, in funzione del parametro λ, le configurazioni di equilibrio interne e le
eventuali configurazioni di equilibrio di confine;
2) Usando le equazioni cardinali della statica, riconoscere che la configurazione C0 individuata da θ = 0
e ξ = 0 è di equilibrio. Determinare, poi, per quali valori della costante elastica k essa risulti stabile;
3) Scrivere le equazioni di Lagrange del moto;
4) Studiare le piccole oscillazioni del sistema intorno alla configurazione C0 (0, 0) .
n
P
u
B
OG = R/2
O
x
ξ
θ
A
y
G
PROVA SCRITTA DI MECCANICA RAZIONALE (20 dicembre 2005)
(C.d.L. Ing. Edile-Architettura ∼ Prof. A. Muracchini)
Il sistema rappresentato in figura, posto in un piano verticale Oxy, è costituito da:
a) un disco circolare omogeneo (massa m, raggio r), vincolato a rotolare senza strisciare sull’asse Ox;
b) un punto materiale pesante P (massa m), posto all’estremità di un’asta rigida di massa trascurabile
e di lunghezza r incernierata nel punto Q = (0, r).
Oltre alla forze peso agiscono sul sistema le forze elastiche dovute all’azione di due molle ideali di
eguale costante elastica k(> 0) agenti fra P e il baricentro G del disco e fra G e la sua proiezione Go
sull’asse Oy (vedi figura).
Assunte come variabili lagrangiane l’ascissa q del centro G del disco e l’angolo θ rappresentato in figura
si chiede:
1) Determinare le configurazioni di equilibrio del sistema discutendone l’esistenza e la stabilità in
funzione del parametro adimensionale λ = mg/kr (> 0);
2) Scrivere le equazioni di Lagrange del moto del sistema;
3) Scrivere le equazioni linearizzate del moto intorno alla configurazione di equilibrio stabile che si ha
per λ = 1.
Supposto, ora, che al sistema venga imposto l’ulteriore vincolo q(t) = r (∀t) si chiede:
4) Cosa si può dire, per λ = 2, sul moto del sistema ad un grado di libertà cosı̀ ottenuto?
q
Go
G
r
O
C
r
Q
r
θ
y
P
x
PROVA SCRITTA DI MECCANICA RAZIONALE (28 gennaio 2006)
(C.d.L. Ing. Edile-Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, mobile in un piano verticale Oxy, è costituito di due aste rigide AB e BC
omogenee, entrambe di massa M e lunghezza l, incernierate tra loro in B e con i loro estremi
A e C vincolati a scorrere, senza attrito, sull’asse orizzontale Ox. Oltre alle forze peso sono
applicate al sistema le seguenti forze:
a) una forza elastica FA = kAO (k > 0) applicata al punto A dell’asta AB;
b) una forza elastica FC = kCQ [con k > 0 , Q ≡ (2l, 0)] applicata all’estremo C dell’asta BC.
Introdotti i parametri lagrangiani θ e xB rappresentati in figura, si chiede:
1) Determinare il valore della costante elastica k per il quale la posizione Po (θ = π/6, xB = l)
risulta di equilibrio per il sistema e verificare che tale posizione è stabile;
2) Scrivere le equazioni di Lagrange del moto e determinare la classe di moti del sistema tali
che θ(t) = costante = π/6;
3) Studiare le piccole oscillazioni del sistema intorno alla posizione di equilibrio stabile Po .
A
O
C
Q
x
θ
XB
y
B
PROVA SCRITTA DI MECCANICA RAZIONALE (10 giugno 2006)
(C.d.L. Ing. Edile-Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, posto in un piano verticale Oxy, è costituito di un disco omogeneo D (massa
m, raggio r) vincolato a rotolare senza strisciare lungo l’asse Ox e di un’asta AB omogenea
(massa m, lunghezza 4r) incernierata nell’estremo B al baricentro G1 del disco. Il disco D
resta, durante il suo moto, nel quadrante positivo mentre il baricentro G dell’asta deve restare
sulla semiretta x = 2r, y ≥ 0.
Oltre alle forze peso, agisce sul sistema la forza elastica dovuta all’azione di una molla di
costante elastica k (k > 0) che collega il punto G1 al punto di coordinate (2r, 0) (vedi figura).
Supposti i vincoli ideali, assunto come parametro lagrangiano l’angolo θ rappresentato in figura,
introdotto il parametro adimensionale λ = mg/kr ∈ <+ , si chiede:
1) Determinare, in funzione di λ, le configurazioni di equilibrio interne e di confine studiando
la stabilità di quelle interne;
2) Calcolare le reazioni vincolari interne ed esterne in una configurazione di equilibrio interna
(con l’asta non verticale);
3) Scrivere l’equazione differenziale del moto di Lagrange;
4) Per λ = 1, studiare le piccole oscillazioni del sistema intorno alla posizione di equilibrio
stabile.
y
A
x= 2 r
G
θ
B
G1
O
Q
C
x
PROVA SCRITTA DI MECCANICA RAZIONALE (28 giugno 2006)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, mobile in un piano verticale, è costituito di un’asta AB rigida omogenea (massa
m, lunghezza 4l) incernierata in O e di un punto P (massa m/2) scorrevole, senza attrito, su di essa.
Oltre alle forze peso sono applicate al sistema le seguenti forze:
a) la forza elastica, applicata al punto P,
FP =
mg
PG
2l
(G baricentro dell’asta)
b) la forza elastica, applicata all’estremo B dell’asta,
FAB =
mg
BD
2l
(| OD |= l)
Scelti i parametri lagrangiani ξ e θ rappresentati in figura, si chiede:
1) Determinare le configurazioni di equilibrio del sistema e studiarne la stabilità;
2) Ritrovare le configurazioni di equilibrio usando le equazioni cardinali della statica e calcolare la
reazione vincolare che si esercita su P all’equilibrio;
3) Scrivere le equazioni di Lagrange del moto;
4) Imposto l’ulteriore vincolo θ = θ̃ = costante e supposto che sul punto P agisca anche una forza
di resistenza viscosa Fv = −hvP û (h > 0) , studiare il moto di P lungo l’asta e calcolare la reazione
vincolare agente su di esso in condizioni dinamiche.
n
y
u
B
P
ξ
D
G
O
θ
A
x
PROVA SCRITTA DI MECCANICA RAZIONALE (10 luglio 2006)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Il sistema in figura è costituito di un’asta AB rigida omogenea (massa m, lunghezza l) vincolata a
mantenere fisso l’estremo A nell’origine di una terna cartesiana Oxyz (vedi figura). Oltre alla forza
peso è applicata, all’estremo B dell’asta, la forza elastica:
F = kBC
(k > 0)
con C = (0, l, 0).
Scelti i parametri lagrangiani θ (0 < θ < π) e ϕ rappresentati in figura, si chiede:
1) Determinare le configurazioni di equilibrio del sistema e studiarne la stabilità;
2) Calcolare la reazione vincolare che si esercita in O all’equilibrio;
3) Ricavare le equazioni differenziali di Lagrange del moto.
z
ξ
π
η
B
θ
c
3
e
2
e
O=A
e1
C
3
ζ
y
ϕ
x
B*
O ξηζ: sistema di assi solidale con l' asta AB.
(assi O ξ ed O η nel piano π ; l'asse O ζ perpendicolare ad essi)
PROVA SCRITTA DI MECCANICA RAZIONALE (13 settembre 2006)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, mobile nel piano verticale Oxz, è costituito di:
a) una lamina quadrata, omogenea (massa M , lato 2l), vincolata a muoversi mantenendo uno dei suoi
lati sull’asse orizzontale Ox e
b) un’ asta AB omogenea (massa m, lunghezza l), incernierata in A al baricentro C della lamina.
Oltre alle forze peso agisce, sull’estremo B dell’asta, la forza elastica:
F = kBD , (k > 0)
con D ≡ (0, −3l).
Supposti i vincoli ideali e introdotti i parametri lagrangiani x (ascissa del punto C) e θ rappresentati
in figura, si chiede:
1) Verificare che la posizione P̄ ≡ (0, π) è di equilibrio e studiarne, in funzione della costante elastica
k, la stabilità;
2) Ricavare le equazioni differenziali di Lagrange del moto;
3) Supposto che all’ istante t0 sia x(t0 ) = 0, θ(t0 ) = π/2 e l’atto di moto del sistema sia nullo, calcolare
la reazione vincolare che la lamina esercita sull’asta in tale istante ;
4) Si assuma, ora, M = 94 m e k = 2mg
3l . Dopo avere preliminarmente verificato che per tali valori la
posizione P̄ risulta stabile, scrivere le equazioni linearizzate del moto del sistema nell’ intorno di essa.
D
A=C
θ
B
O
x
z
x
PROVA SCRITTA DI MECCANICA RAZIONALE (13 dicembre 2006)
(C.d.L. Ing. Edile - Architettura ∼ Prof. A. Muracchini)
Il sistema rappresentato in figura, mobile in un piano verticale Oxy, è costituito di un’asta OA
omogenea (massa m, lunghezza 2l) incernierata in O e vincolata a restare appoggiata su uno
spigolo T di una lamina rettangolare omogenea (massa m, lati di lunghezza l e 2l) scorrevole,
senza attrito, lungo l’asse Ox (M ed N punti di appoggio della lamina). Oltre alle forze peso,
è applicata alla lamina la forza elastica F = −kQG2 [k > 0 e Q ≡ (l, 0)]. Tutti i vincoli sono
supposti ideali.
Assunto come parametro lagrangiano l’angolo θ rappresentato in figura e posto λ = kl/mg(> 0)
si chiede:
1) Determinare, discutendole in funzione del parametro λ, le configurazioni di equilibrio interne
e di confine del sistema esaminando la stabilità di quelle interne;
2) Calcolare, all’equilibrio (configurazioni interne), le reazioni vincolari che si esercitano sull’asta
OA;
3) Rappresentare la funzione lagrangiana L del sistema.
y
A
T
G1
G2
mg
l
mg
θ
O
Q
l
M
2l
N
x
PROVA SCRITTA DI MECCANICA RAZIONALE (19 gennaio 2007)
(C.d.L. Ing. Edile-Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, mobile nel piano verticale Oxy, è costituito di una circonferenza C pesante,
omogenea (massa M , raggio R) vincolata in modo che il punto A del suo bordo sia mobile sull’asse
verticale Oy. Sul punto B della circonferenza, diametralmente opposto ad A, agisce una forza elastica
F = kBO(k > 0).
Supposti i vincoli ideali, scelti i parametri lagrangiani yA e θ rappresentati in figura e introdotto il
parametro adimensionale λ = kR/M g ∈ <+ si chiede:
1) Determinare le configurazioni di equilibrio del sistema e studiarne la stabilità in funzione del parametro λ. Stabilire se esistono valori della costante elastica k tali che il sistema sia in equilibrio nella
posizione yA = −R, θ = π;
2) Calcolare la reazione vincolare che si esercita in A all’equilibrio;
3) Scrivere le equazioni di Lagrange del moto;
4) Dopo avere preliminarmente verificato che, per λ = 1/2, esiste ed è stabile la posizione di equilibrio
yA = 0, θ = π, studiare le piccole oscillazioni del sistema intorno a tale configurazione.
O
x
y
A
A
C
θ
.
B
y
PROVA SCRITTA DI MECCANICA RAZIONALE (15 giugno 2007)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Il sistema rappresentato in figura, mobile in un piano orizzontale Oxy, è costituito di un arco omogeneo
di semicirconferenza (massa m, raggio R) incernierato in O.
Al sistema sono applicate le seguenti forze:
a) una forza elastica Fel. = kAAo (k > 0), applicata al punto A, dovuta alla azione di una molla ideale
che si mantiene sempre parallela all’asse Oy (vedi figura);
b) una forza di resistenza viscosa, F(v) = −hvA (h > 0), che si esercita sul punto A;
c) una coppia di momento M = Mk (M > 0 costante, k =vers Oz).
Supposti i vincoli ideali, utilizzando il parametro lagrangiano θ rappresentato in figura si chiede:
1) Scrivere le equazioni cardinali della dinamica e calcolare la reazione vincolare che si esercita nella
cerniera O sia in condizioni dinamiche che in condizioni statiche;
2) Determinare in funzione del parametro λ = M/2kR2 le configurazioni di equilibrio del sistema;
3) Ottenere l’equazione differenziale di Lagrange del moto;
4) Nel caso k = 0 (forza elastica nulla), supposto che all’istante t = 0 la velocità angolare del sistema
sia ω(0) = ω0 , calcolare il tempo τ dopo il quale tale velocità si riduce al valore ω0 /2.
y
z
A
k
y
A
j
θ
O
x
O i
A0
θ
A0
x
PROVA SCRITTA DI MECCANICA RAZIONALE (10 luglio 2007)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, mobile nel piano verticale Oxy, è costituito di un’ asta rigida di massa trascurabile,
il cui centro C è vincolato a muoversi, senza attrito, lungo l’asse Ox. Agli estremi dell’asta sono saldati
due punti materiali: A (massa m) e B (massa 2m)
Oltre alle forze peso agiscono sul sistema:
a) la forza elastica Fe = kAH [k > 0, H ≡ (0, 2l) → vedi figura];
b) la forza costante F = F i [F > 0] applicata nel centro C dell’asta;
c) una coppia di momento M = Mk [M costante; k versore dell’asse Oz].
Introdotti i parametri lagrangiani x (ascissa del punto C) e θ rappresentati in figura, si chiede:
1) Calcolare il valore del momento M da applicare al sistema affinchè esso sia in equilibrio per θe = π/2
ed il valore xe in tale configurazione di equilibrio. Studiare, poi, la stabilità della posizione di equilibrio
P=(θe , xe );
2) Calcolare la reazione vincolare che si esercita in C sia in condizioni dinamiche che nella posizione
di equilibrio P trovata nella precedente domanda;
3) Ricavare le equazioni differenziali di Lagrange del moto;
4) Supposto, ora, che sul sistema non agiscano la forza elastica e la forza F si chiede di determinare
eventuali integrali primi del moto e di interpretarli fisicamente.
y
H
2l
A (m)
l
θ
x
O
x
i
C
l
B (2m)
F
PROVA SCRITTA DI MECCANICA RAZIONALE (10 settembre 2007)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, mobile in un piano verticale Oxy, è costituito di un’asta omogenea AB (massa m,
lunghezza 2l) vincolata a scorrere, senza attrito, entro il cursore posto in O (vedi figura).
Oltre al peso, sono applicate al sistema le seguenti forze:
a) la forza elastica F = kAQ(k > 0) che richiama l’estremo A dell’asta verso il punto Q dell’asse Oy
(yQ = l);
b) una coppia di momento M = M k costante.
Introdotti i parametri lagrangiani θ e ξ rappresentati in figura si chiede:
1) scrivere le equazioni di equilibrio dell’asta AB utilizzando: a] il potenziale e b] le equazioni cardinali
della statica;
2) verificare che, assunto k = 2mg/l, la posizione θo = π/3, ξo = 7l/4 può essere di equilibrio
determinando il valore da attribuire alla coppia M perchè tale equilibrio sussista;
3) studiare, nel caso di equilibrio della domanda precedente, la stabilità della configurazione θo , ξo ;
4) rappresentare la funzione lagrangiana L del sistema;
5) scrivere le equazioni linearizzate del moto nell’ intorno della eventuale posizione di equilibrio stabile
θo , ξo .
y
Q
A
O
x
θ
ξ
n
B
u
PROVA SCRITTA DI MECCANICA RAZIONALE (7 dicembre 2007)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, mobile nel piano verticale Oxy, è costituito di due aste rigide AB e CD, omogenee,
entrambe di massa M e lunghezza 2l. L’asta AB ha gli estremi A e B vincolati a scorrere, senza attrito,
sugli assi Ox ed Oy, rispettivamente. L’ asta CD è vincolata a muoversi mantenendo il suo estremo C
incernierato al punto medio H dell’asta AB. All’ estremo D dell’asta CD è applicata la forza elastica
Fe = kDO [k > 0, vedi figura].
Supposti i vincoli ideali e introdotti i parametri lagrangiani θ e ϕ rappresentati in figura, si chiede:
1) Dimostrare che, per k < M g/3l, la posizione corrispondente a θ = 0 e ϕ = 0 risulta di equilibrio
stabile;
2) Ricavare le equazioni differenziali di Lagrange del moto;
3) Scrivere le equazioni linearizzate del moto intorno alla posizione di equilibrio stabile studiata nella
domanda 1).
4) Si assuma ora k = M g/2l. Supposto che all’ istante iniziale (t0 ) del moto il sistema si trovi nella
configurazione θ = 0 e ϕ = π/2 e possieda atto di moto nullo, si chiede di calcolare in tale istante :
4a) l’accelerazione del baricentro dell’ asta CD;
4b) la reazione vincolare che l’ asta AB esercita sull’asta CD in C.
A
O
x
θ
H
C
ϕ
B
y
D
PROVA SCRITTA DI MECCANICA RAZIONALE (11 gennaio 2008)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, mobile nel piano verticale Oxy, è costituito di una lamina rettangolare rigida,
omogenea, di massa M , il cui lato AB è vincolato a scorrere su una retta orizzontale λ. Nella lamina
è praticato un foro circolare (γ) di raggio r e centro C sul bordo del quale è vincolato a muoversi,
senza potersene distaccare, un punto materiale P di massa m (vedi figura). Su di esso agisce la forza
elastica Fe = −kAP [ k = mg/2r , A ≡ (0, −2r) ].
Supposti i vincoli ideali, scelto il sistema di riferimento Oxy indicato in figura e introdotti i parametri
lagrangiani x (ascissa del centro C del disco) e θ, si chiede:
1) Determinare le configurazioni di equilibrio del sistema e studiarne la stabilità;
2) Calcolare il valore della reazione vincolare che si esercita sul punto P nelle posizioni di equilibrio
stabile;
3) Scrivere le equazioni differenziali di Lagrange del moto;
4) Determinare le frequenze delle piccole oscillazioni del sistema, nell’intorno di una configurazione di
equilibrio stabile.
A
2r
O
C
θ
γ
x
P
r
xC
A
B
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
y
λ
PROVA SCRITTA DI MECCANICA RAZIONALE (19 aprile 2008)
(C.d.L. Ing. Edile/Architettura - Prof. A. Muracchini)
Il sistema in figura, posto in un piano verticale Oxy, è costituito da:
a) una lamina rettangolare ABCD (lati 2l, 4l), omogenea, di massa M , vincolata a muoversi mantenendo il suo lato BC a contatto con l’asse Ox;
b) un’asta ST, omogenea (massa m, lunghezza l) i cui estremi sono vincolati a scorrere (senza attrito)
sugli assi del rettangolo.
Oltre alle forze peso, agisce sul sistema la forza elastica F = kAQ (k > 0) dovuta all’azione di una
molla che collega il vertice A della lamina al punto Q ≡ (0, 3l).
Supposti i vincoli ideali e assunti come parametri lagrangiani l’ascissa x del punto A e l’angolo di
rotazione θ dell’asta (vedi figura) si chiede:
1) Determinare le configurazioni di equilibrio del sistema e studiarne la stabilità;
2) Ricavare le equazioni differenziali di Lagrange del moto;
3) Posto M = m e k = 3M g/2l, scrivere le equazioni linearizzate del moto nell’intorno della posizione
di equilibrio stabile e determinare le frequenze delle piccole oscillazioni.
α
y
θ
Q
D
A
T
θ
S
O
B
x
C
x
PROVA SCRITTA DI MECCANICA RAZIONALE (20 giugno 2008)
(C.d.L. Ing. Edile - Architettura ∼ Prof. A. Muracchini)
Il sistema rappresentato in figura è costituito da una lamina quadrata omogenea (massa M , lato 2l)
vincolata mediante una cerniera ad asse orizzontale e da un punto materiale P (massa M ) vincolato
a muoversi, senza uscirne, lungo la guida MN della lamina passante per il baricentro e ortogonale
all’asse della cerniera. Sul punto P , oltre al peso, agisce la forza elastica F = −kAP (k = 4M g/3l)
essendo A un punto fisso posto a distanza l al di sopra dell’asse della cerniera. Tutti i vincoli sono
supposti ideali.
Scelto un sistema di riferimento Oxyz il cui asse Oy coincide con l’asse della cerniera e con l’asse Oz
passante per A e orientato verso il basso, si assumano i parametri lagrangiani ξ e θ rappresentati in
figura. Si chiede:
1) Determinare le configurazioni di equilibrio interne e le eventuali configurazioni di equilibrio di
confine, discutendo la stabilità di quelle interne;
2) Determinare la reazione vincolare che si esercita nel punto P sia all’equilibrio che durante il moto;
3) Ricavare le equazioni differenziali di Lagrange;
4) Stabilire sotto quali condizioni siano possibili moti del sistema con la lamina in quiete (Suggerimento:
porre θ = θ0 = costante, nelle equazioni del moto...).
A
O
x
M
ξ
P
G
y
N
ξ
θ
z
1
PROVA SCRITTA DI MECCANICA RAZIONALE (8 luglio 2008)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, posto in un piano verticale Oxy, è costituito da una lamina rettangolare ABCD
(lati a, b ; a < b), omogenea, di massa M , vincolata a muoversi mantenendo il suo baricentro G
sull’asse Ox.
Oltre alla forza peso, agisce sul sistema la forza elastica F = kGO (k > 0) dovuta all’azione di una
molla che collega il baricentro G della lamina all’origine O del sistema Oxy.
Supposti i vincoli ideali e assunti come parametri lagrangiani l’ascissa x del baricentro G e l’angolo di
rotazione θ della lamina (vedi figura) si chiede:
1) Scrivere l’equazione dell’ellissoide centrale d’inerzia e calcolare il momento d’inerzia della lamina
rispetto all’asse YG rappresentato in figura;
2) Studiare il moto del sistema usando le equazioni cardinali della dinamica.
−
Supponiamo, ora, che il piano Oxy in cui giace la lamina ruoti con velocità angolare costante →
ω intorno
all’asse verticale Oy. In tali condizioni si chiede:
3) Determinare le posizioni di equilibrio del sistema e studiarne la stabilità nei casi M ω 2 ≷ k;
4) Ricavare le equazioni differenziali di Lagrange del moto;
5) Quando M ω 2 = k, cosa si può dire: a) sull’equilibrio e b) sul moto della lamina?
y
YG
ω
D
C
G
O
θ
x
x
A
b
a
B
PROVA SCRITTA DI MECCANICA RAZIONALE (12 settembre 2008)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, posto in un piano verticale Oxy, è costituito da una semicirconferenza omogenea γ
(raggio 3r, massa m) vincolata a traslare lungo l’asse Ox e da un disco D omogeneo (raggio r, massa
m) che rotola senza strisciare, internamente, sulla semicirconferenza suddetta senza uscirne.
Oltre alle forze peso, agisce sul sistema la forza elastica F = kAO (k = mg/r) dovuta all’azione di
una molla che collega il punto A di γ all’origine O del sistema Oxy.
Supposti i vincoli ideali e assunti come parametri lagrangiani l’ascissa xA del punto A e l’angolo θ tra
la direzione O0 T (O0 centro della semicirconferenza, T punto di contatto tra D e γ) e la verticale O0 A
(vedi figura) si chiede:
0) Rappresentare: a) la velocità angolare del disco e b) usando i risultati della cinematica dei moti
relativi, la velocità assoluta del baricentro G del disco;
1) Determinare, con le equazioni cardinali della statica, le configurazioni di equilibrio del sistema e
calcolare le reazioni vincolari esterne ed interne. Studiare, poi, la stabilità delle configurazioni trovate;
2) Ricavare le equazioni di Lagrange del moto;
3) Scrivere le equazioni linearizzate del moto intorno alla configurazione di equilibrio stabile e calcolare
le frequenze caratteristiche.
q
Supponiamo, ora, che venga imposto l’ulteriore vincolo θ(t) = 2g
r t. In tale situazione si chiede:
4) Ricavare l’equazione differenziale del moto del sistema e scriverne l’integrale generale.
O
y
γ
θ
eθ
D
3r
G
r
T
O
xA
A
X
PROVA SCRITTA DI MECCANICA RAZIONALE (10 dicembre 2008)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Nel piano orizzontale Oxy, un disco D, pesante, omogeneo (massa M , raggio R) è vincolato a ruotare
intorno ad un asse fisso Oz ortogonale al piano e passante per O (vedi figura). Un punto P (massa m)
è mobile, senza attrito, entro il diametro OA del disco e su di esso agisce la forza elastica F = −kCP
(k > 0, C centro del disco).
Supposti i vincoli ideali e assunti come parametri lagrangiani θ e x rappresentati in figura si chiede:
1) Ricavare le equazioni differenziali di Lagrange del moto ed individuare eventuali integrali primi;
2) Esaminare se esistono moti del sistema con θ̇ = costante.
Supponiamo, ora, che il disco ruoti con velocità angolare Ω=costante. In tali condizioni si chiede:
3) Determinare, discutendone l’esistenza in funzione di Ω, le posizioni di equilibrio relativo, interne e
di confine, del punto P . Studiare, poi, la stabilità di quelle interne;
4) Ricavare l’equazione differenziale del moto di P lungo il diametro OA ed integrarla.
z
y
D
P
C
A
+
x
O
θ
x
PROVA SCRITTA DI MECCANICA RAZIONALE (16 gennaio 2009)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, posto nel piano orizzontale Oxy, è costituito di due punti materiali: P (massa
m) e Q (massa M ).
Il punto P può muoversi su tutto l’ asse Ox mentre il punto Q è vincolato a scorrere sulla semicirconferenza γ (raggio r, centro O) senza uscirne. Sul sistema agiscono forze elastiche dovute all’ azione
di una molla ideale (di costante elastica k > 0) che collega i due punti come in figura.
Supposti i vincoli ideali e introdotti i parametri lagrangiani x e θ rappresentati in figura, si chiede:
1) Determinare le configurazioni di equilibrio interne e di confine e studiare, poi, la stabilità di quelle
interne. Studiare le configurazioni di equilibrio nel caso che il piano Oxy del sistema sia verticale (per
questa parte della domanda si introduca il parametro adimensionale λ = M g/kr ∈ <+ );
2) Ricavare ed integrare il sistema delle equazioni linearizzate del moto intorno alla posizione di
equilibrio stabile;
3) Scrivere le equazioni di Lagrange: a) nelle condizioni descritte nel testo del problema e b) supponendo che sul punto Q agisca anche una forza di resistenza viscosa F = −hvQ (h > 0).
Supponiamo, ora, che venga imposto l’ulteriore vincolo θ̇(t) = Ω = costante. In tale situazione si
chiede:
4) Ricavare ed integrare l’equazione differenziale del moto del punto P.
y
Q
r
P
θ
O
γ
x
x
PROVA SCRITTA DI MECCANICA RAZIONALE (8 aprile 2009)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, mobile nel piano verticale Oxy, è costituito di una circonferenza γ, omogenea
(massa M , raggio R) di centro C vincolata, mediante una cerniera piana, nel punto A e di un punto
pesante P (massa m) vincolato, senza attrito, a muoversi lungo γ.
Supposti i vincoli ideali, e introdotti i parametri lagrangiani θ e ϕ rappresentati in figura, si chiede:
1) Determinare le configurazioni di equilibrio del sistema e studiarne la stabilità;
2) Usando le equazioni cardinali della statica, ritrovare le configurazioni di equilibrio del sistema e
determinare le reazioni vincolari che si esercitano nella cerniera A e nel punto P ;
3) Scrivere l’energia cinetica del sistema;
4) Ricavare le equazioni linearizzate del moto intorno alla posizione di equilibrio stabile.
Α= O
x
θ
P
R
C
ϕ
γ
y
PROVA SCRITTA DI MECCANICA RAZIONALE (11 giugno 2009)
(C.d.L. Ing. Edile/Architettura ∼ Prof. A. Muracchini)
Il sistema in figura, posto in un piano verticale Oxy, è costituito da:
a) una lamina omogenea, pesante, di forma circolare (massa 3M , raggio 2r, centro O) con un foro
0
(raggio r, centro O posto a distanza r da O) e vincolata in O con una cerniera piana;
b) un punto P (massa M ) vincolato a scorrere, senza uscirne, lungo il diametro della lamina ortogonale
0
a quello passante per O .
Oltre alle forze peso, agisce sul sistema la forza elastica F = kP C (k > 0) dovuta all’azione di una
molla che collega il punto P al punto C posto sulla verticale per O, al di sopra di quest’ultimo e a
distanza d = M g/k da esso.
Supposti i vincoli ideali e assunti come parametri lagrangiani ρ e θ (vedi figura) si chiede:
1) Determinare il baricentro della lamina e la matrice centrale principale d’inerzia;
2) Determinare le configurazioni di equilibrio ordinarie e di confine del sistema discutendo la stabilità
di quelle ordinarie;
3) Calcolare le reazioni vincolari che si esercitano nella cerniera O e nel punto P all’equilibrio e in
condizioni dinamiche;
4) Ricavare le equazioni di Lagrange del moto;
5) Studiare le piccole oscillazioni del sistema intorno alla configurazione di equilibrio stabile.
C
r
2r
O
x
ρ
P
θ
y
PROVA SCRITTA DI MECCANICA RAZIONALE (9 luglio 2009)
(C.d.L. Ing. Edile/Architettura (A-K) ∼ Prof. A. Muracchini)
In un piano verticale Oxy sono mobili due punti materiali pesanti P1 , P2 , di masse rispettive m1 e
m2 , collegati da un’asta rigida di lunghezza 3l e massa trascurabile. Il punto A dell’asta, distante l
da P1 , è scorrevole senza attrito sull’asse Oy verticale (vedi figura) ed è attratto verso O da una forza
elastica F = −kOA (k > 0 assegnato).
Supposti i vincoli ideali ed assunte come variabili lagrangiane y = yA e θ (vedi figura), si chiede:
1) Determinare le configurazioni di equilibrio del sistema, discutendone la stabilità. Ritrovare, poi,
tali configurazioni usando le equazioni cardinali della statica.
Supponiamo, ora, che il piano in cui giace il sistema sia posto in rotazione, intorno all’asse fisso Oy,
con velocità angolare costante ω. In tale situazione si chiede:
2) Rappresentare, usando il teorema di composizione delle velocità, le velocità assolute di P1 e P2 .
Nel caso in cui sia m1 = 2m2 :
3) Ricavare le configurazioni di equilibrio relativo del sistema e studiarne la stabilità;
4) Scrivere le equazioni di Lagrange del moto relativo.
x
y
y
ω
ω
j
i
O
x
O
ωt
yA
P1
m1g
A
A
P1
2
θ
P2
m2g
P2