Dispositivi e Sistemi Meccanici
Politecnico di Torino
CeTeM
3
Esercizi
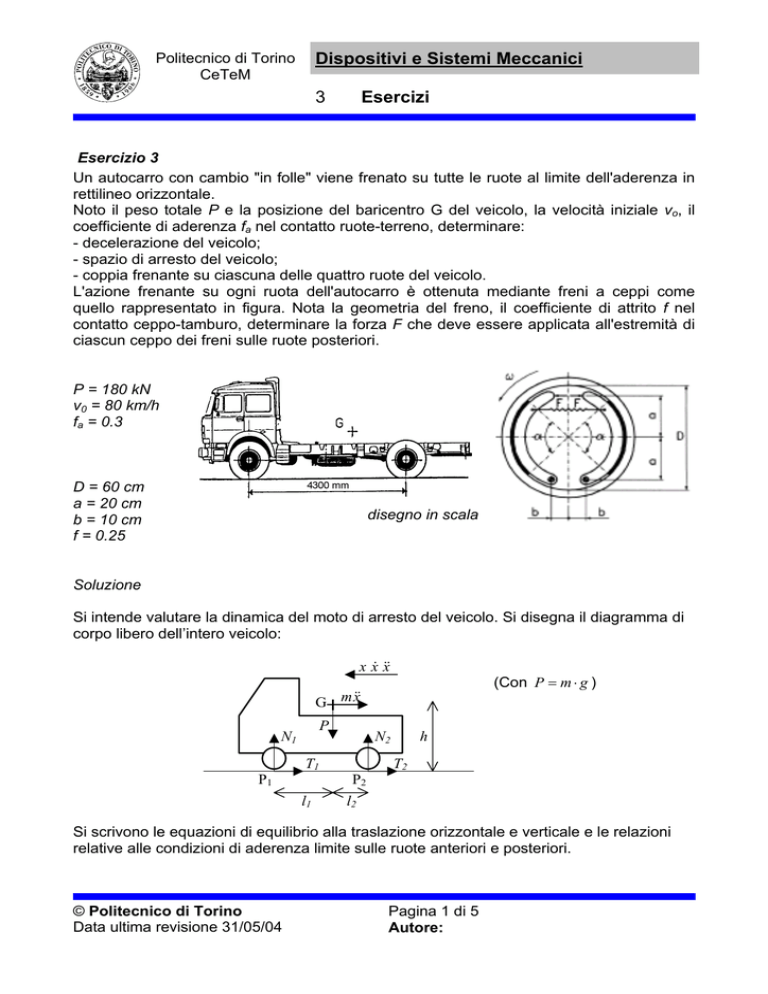
Esercizio 3
Un autocarro con cambio "in folle" viene frenato su tutte le ruote al limite dell'aderenza in
rettilineo orizzontale.
Noto il peso totale P e la posizione del baricentro G del veicolo, la velocità iniziale vo, il
coefficiente di aderenza fa nel contatto ruote-terreno, determinare:
- decelerazione del veicolo;
- spazio di arresto del veicolo;
- coppia frenante su ciascuna delle quattro ruote del veicolo.
L'azione frenante su ogni ruota dell'autocarro è ottenuta mediante freni a ceppi come
quello rappresentato in figura. Nota la geometria del freno, il coefficiente di attrito f nel
contatto ceppo-tamburo, determinare la forza F che deve essere applicata all'estremità di
ciascun ceppo dei freni sulle ruote posteriori.
P = 180 kN
v0 = 80 km/h
fa = 0.3
D = 60 cm
a = 20 cm
b = 10 cm
f = 0.25
disegno in scala
Soluzione
Si intende valutare la dinamica del moto di arresto del veicolo. Si disegna il diagramma di
corpo libero dell’intero veicolo:
x x& &x&
(Con P = m ⋅ g )
G m &x&
P
N1
P1
T1
l1
N2
P2
h
T2
l2
Si scrivono le equazioni di equilibrio alla traslazione orizzontale e verticale e le relazioni
relative alle condizioni di aderenza limite sulle ruote anteriori e posteriori.
© Politecnico di Torino
Data ultima revisione 31/05/04
Pagina 1 di 5
Autore:
Politecnico di Torino
CeTeM
Dispositivi e Sistemi Meccanici
3
Esercizi
→ T1 + T2 + m x& = 0
↑ N 1 + N 2 − P = 0
ad.lim. T1 = f a ⋅ N 1
T2 = f a ⋅ N 2
Risolvendo si avrà:
f a (N 1 + N 2 ) + m x& = 0
⇒
N1 + N 2 = 0
f a ⋅ P + m &x& = 0 ⇒
&x& = − f a ⋅
P
m
= − f a ⋅ g = −2,943 2
m
s
Nota la decelerazione del veicolo, si determina lo spazio di arresto, integrando due volte
l’espressione dell’accelerazione:
t
v
dv
⇒ ∫ a dt = ∫ dv ⇒ at = v − v0 ⇒ at + v0 = v
v0
0
dt
t
x
1 2
dx
ma v =
allora ∫ (at + v0 ) dt = ∫
dx ⇒
a t + v0t = x
0
2
dt
0 ax
=0
a = &x& =
iniziale
Essendo
tarresto = t*
Spazio arresto = x*
1
2
a t * + v 0 t* = x *
⇒
2
a t* = − v0
x* = −
v02
= 83,9 m
2a
Per valutare la coppia frenante su ciascuna ruota del veicolo, sono necessari alcuni dati
geometrici, rilevabili dal disegno in scala:
l1 = 2900 mm = 2,9 m
l2 = 1,4 m
h = 1,4 m
r = 500 mm = 0,5 m
Si scrive l’equazione di equilibrio alla rotazione intorno a P1:
P1
N 2 (l1 + l 2 ) − P l1 − m &x& h = 0
sostituendo la (1) e individuando con l = l1 + l2
N2 =
1
(P l1 − f a P h ) = P (l1 − f a h ) = 103,8 kN
l
l
© Politecnico di Torino
Data ultima revisione 31/05/04
Pagina 2 di 5
Autore:
Politecnico di Torino
CeTeM
Dispositivi e Sistemi Meccanici
3
Esercizi
dall’equilibrio alla traslazione verticale:
N 1 = P − N 2 = 76,2 kN
dalle equazioni di aderenza limite:
T1 = 22,9 kN
T2 = 31,1 kN
per calcolare la coppia frenante si disegnano i diagrammi di corpo libero delle ruote, e si
imporà l’equilibrio alla rotazione scegliendo come polo dei momenti il centro delle ruote,
tenendo conto che le forze saranno dimezzate rispetto ai valori precedenti perché sono
presenti due ruote per ogni assale.
Ruota anteriore.
Cf1
r1
N1/2
Cf1 =
T1
r = 5,7 kN m
2
Cf2 =
T2
r = 7,8 kN m
2
T1/2
Ruota posteriore.
Cf2
R2
N2/2
T2/2
Si considera la geometria di un freno a tamburo sulla ruota posteriore. Per tracciare il
diagramma di corpo libero si fa l’IPOTESI SEMPLIFICATIVA che le forze scambiate fra
ceppo e tamburo (RS e RD) siano applicate nel PUNTO MEDIO della superficie di contatto
ceppo-tamburo. Si osserva inoltre che la forza F applicata al ceppo destro e sinistro sarà
uguale perché sviluppata da dispositivo uguali, per esempio cilindretti attuatori, che
sviluppano una stessa forza essendo attuati da una stessa pressione di un circuito
idraulico comune.
© Politecnico di Torino
Data ultima revisione 31/05/04
Pagina 3 di 5
Autore:
Politecnico di Torino
CeTeM
Dispositivi e Sistemi Meccanici
3
Esercizi
ω
F F
RS
NS
TS
ND
bRD TD
bRS N /2
2
RD
T2/2
b b
DCL del tamburo.
ω
TS
V0
N0
O
NS
ND
O
TD
N2/2
T2
D
r = (TS + TD ) = C f 2
2
2
TS = f NS
TD =f ND
(1)
(2)
(3)
T2/2
DCL del ceppo sinistro.
F
TS
NS
OS
D
F ⋅ 2a + TS − b − N S a = 0
2
D
⇒ F ⋅ 2a = −TS − b + N S a
2
(4)
OD
D
TD − b + N D a − F ⋅ 2a = 0
2
D
⇒ F ⋅ 2a = TD − b + N D a
2
(5)
VS
NS
OS
DCL del ceppo destro.
F
ND
TD
VD
ND
OD
© Politecnico di Torino
Data ultima revisione 31/05/04
Pagina 4 di 5
Autore:
Politecnico di Torino
CeTeM
Dispositivi e Sistemi Meccanici
3
Esercizi
Risolvendo il sistema:
(4) e (5)
D
D
− TS − b + N S a = TD − b + N D a
2
2
Sostituisco le (2) e (3)
a D
+ − b
f
2
a D
a D
− TS − + b = TD + − b ⇒ TS = TD
2
a D
f 2
f
− + b
f 2
sostituendo in (1)
T2
r = Cf 2
2
= TD
a D
+ −b
b
f
2
+ 1 ⋅
a D
− +b 2
f 2
a D
a D
− +b
− +b
2C f
C
f 2
2
f f
⇒ TD =
=
a
D
a
D
a
D
− +b+ + −b D
f 2
f
2
f
f Cf a D
− + b = 9750 N
Da f 2
TS = 16250 N
ND = 39000 N
NS = 65000 N
F = 24375 N
TD =
N.B. ricavando ancora
RS = TS2 + N S2 = 67 kN
RD = TD2 + N D2 = 40,2 kN
Si osserva che RS > RD perché il braccio di RS rispetto ad OS é minore del braccio di RD
rispetto ad OV (vedi figura).
© Politecnico di Torino
Data ultima revisione 31/05/04
Pagina 5 di 5
Autore:












