APPLICAZIONI DELLA DERIVATA IN FISICA

INTERPRETAZIONE CINEMATICA DELLA DERIVATA
Consideriamo un punto mobile sopra una qualsiasi linea. Fissiamo su tale linea
un punto O, come origine degli archi, e un verso di percorrenza come verso positivo;
in tal modo possiamo far corrispondere a ciascun punto P della curva la lunghezza s
dell'arco OP, presa positiva o negativa a seconda che OP sia concorde o discorde
con il verso fissato come positivo sulla curva. Si usa dire che s è l’ascissa
curvilinea del punto P e, se P si muove sulla curva al variare del tempo t, allora
s sarà funzione di t e si scriverà s = s(t). L'ascissa curvilinea s prende anche il
nome di spazio percorso a partire dall'istante iniziale, quando cioè il punto P si
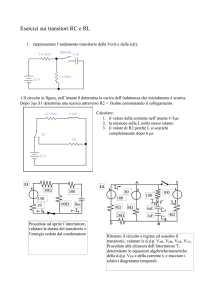
trovava in O. Consideriamo la figura seguente:
t
O
P
t+∆t
Q
P è la posizione del punto mobile all'istante t e s = s(t) è lo spazio
percorso a tale istante; se dopo un intervallo di tempo Δt, cioè all'istante t +
Δt, il punto mobile si troverà in Q, lo spazio percorso a quell'istante sarà s(t +
Δt).
Osserviamo dunque che all'incremento Δt della variabile tempo corrisponde,
per lo spazio, l'incremento
Δs = s(t + Δt) - s(t)
che rappresenta lo spazio percorso nel tempo Δt.
Consideriamo ora il rapporto Δs/Δt tra lo spazio percorso e l'intervallo di
tempo impiegato a percorrerlo
∆s s (t + ∆t ) − s (t )
=
∆t
∆t
che, come sappiamo dalla fisica, rappresenta la velocità media del punto mobile nel
tempo Δt. Ma tale rapporto è anche il rapporto incrementale della funzione spazio
relativo all'istante generico t e all'incremento Δt.
Facciamo tendere a zero l'incremento Δt del tempo: sappiamo che, così facendo,
la velocità media tende, in generale, a un limite v che rappresenta la velocità
istantanea o velocità all'istante t. E sarà v funzione di t, v = v(t), perché v
varierà al variare dell'istante generico t considerato.
D'altra parte, se Δt tende a zero, il rapporto incrementale, se ammette
limite, tende alla derivata della funzione s rispetto alla variabile t:
lim
∆t → 0
∆s
= s ' (t )
∆t
Si può così concludere che la velocità istantanea è la derivata dello spazio
percorso rispetto al tempo:
tempo:
v = s'
o meglio
v (t ) = s ' (t )
ds
.
dt
»»»»»»» «««««««
In fisica si preferisce scrivere: v =
Come abbiamo già osservato, la velocità istantanea è una funzione del tempo t
e quindi nell'intervallo Δt di tempo subirà la variazione
∆v = v(t + ∆t ) − v(t ) .
∆v
rappresenta l'accelerazione media del punto
∆t
mobile nel tempo Δt. Facciamo tendere Δt a zero: se il rapporto incrementale
Il rapporto incrementale
∆v v(t + ∆t ) − v(t )
=
∆t
∆t
tende a un limite finito a, se cioè la funzione v(t) è derivabile, tale limite,
che è la derivata v ' (t ) , rappresenta l'accelerazione istantanea e si avrà quindi
∆v
v(t + ∆t ) − v(t )
dv
= lim
= v' (t ) =
∆t → 0 ∆t
∆t → 0
∆t
dt
a = lim
→
a=
dv
dt
Ma, essendo sua volta v(t ) = s ' (t ) , sarà v' (t ) = s ' ' (t ) e quindi a(t ) = s ' ' (t ) =
d 2s
dt 2
Concluderemo così che l'accelerazione istantanea è la derivata della velocità
rispetto al tempo e quindi è la derivata seconda dello spazio percorso rispetto al
tempo.
tempo.
Esempio:
Sia s = 2t 3 − 3t + 1 la legge oraria del moto di un punto mobile, con s misurato
in metri e t in secondi. Dopo aver determinato velocità e accelerazione in un
generico istante t, calcolare i metri percorsi dal mobile nel tempo che intercorre
tra l'istante in cui la velocità è di 51 m/s e quello in cui l'accelerazione è di
84m/s2.
Si ha
v = s ' (t ) = 6 t 2 − 3
e
a = v' (t ) = 12t .
Si avrà
v = 51
a = 84
→
6t 2 − 3 = 51
→
12t = 84
→
→
t =3
t =7
e quindi, essendo s (7) = 686 − 21 + 1 = 666 e s (3) = 54 − 9 + 1 = 46
lo spazio percorso in quei quattro secondi sarà
(666-46)m = 620m.
ALTRE APPLICAZIONI FISICHE
1. INTENSITÁ DI CORRENTE
Sia q = q(t) la quantità di carica elettrica che nell'intervallo di tempo [0; t ]
attraversa la sezione di un conduttore; diamo a t un incremento Δt e sia q(t + Δt)
la quantità di carica che attraversa la stessa sezione nell'intervallo (0; t + ∆t ) .
Sappiamo che il rapporto
∆q q(t + ∆t ) − q(t )
=
(1)
∆t
∆t
tra la quantità di elettricità che passa nella sezione del conduttore
nell'intervallo di tempo Δt e Δt stesso indica l'intensità media della corrente
elettrica in quel conduttore relativamente all'intervallo di tempo (t ; t + ∆t ) .
Inoltre sappiamo che, se
q (t + ∆t ) − q (t )
(2)
lim
∆t → 0
∆t
esiste ed è finito, esso dà il valore dell'intensità della corrente all'istante t:
q(t + ∆t ) − q(t )
∆t → 0
∆t
Ma tale rapporto altro non è che il rapporto incrementale della funzione q(t) e il
limite (2) è quindi, se esiste, la derivata della funzione q(t). Si conclude così
che è
dq
i (t ) = q ' (t ) =
dt
i (t ) = lim
2. TENSIONE E CORRENTE AI CAPI DI UN CONDENSATORE
Si consideri un condensatore di capacità C supponiamo che C, dipendendo solo
dalle caratteristiche fisiche del condensatore, sia costante al variare del tempo;
sappiamo che
Q = C·V
(3)
è la relazione tra la quantità di carica Q(t), in funzione del tempo, presente
sulle armature del condensatore e la tensione V(t) ai capi del condensatore stesso.
Consideriamo il rapporto incrementale della funzione Q(t) relativamente
all'intervallo di tempo Δt:
∆Q Q(t + ∆t ) − Q(t )
=
∆t
∆t
(4)
esso esprime un'indicazione della variazione della quantità di carica sulle
armature del condensatore, relativa all'intervallo di tempo Δt, cioè esprime
l'intensità media della corrente di carica o di scarica del condensatore
relativamente allo stesso intervallo di tempo. Facendo tendere Δt a zero, il
limite della (4) rappresenterà l'intensità istantanea della corrente di carica o di
scarica:
∆Q
Q(t + ∆t ) − Q(t )
lim
= lim
= i (t ) .
(5)
∆t → 0 ∆t
∆t → 0
∆t
Consideriamo ora la grandezza C·V che figura del secondo membro della (3) e
valutiamo il rapporto tra l'incremento che essa subisce delle intervallo di tempo
Δt e l'incremento Δt stesso, tenendo presente che C è costante nel tempo:
∆(C ⋅ V ) C ⋅ V (t + ∆t ) − C ⋅ V (t )
=
∆t
∆t
da cui
∆(C ⋅ V ) C ⋅ [V (t + ∆t ) − V (t )]
∆V
=
=C⋅
∆t
∆t
∆t
Passiamo ora al limite per Δt che tende a zero, ottenendo
∆(C ⋅ V )
∆V
dV
= C ⋅ lim
=C⋅
∆t → 0
∆t → 0 ∆t
∆t
dt
lim
(6)
Per la (3), possiamo dedurre che i secondi membri della (5) e della (6) devono
essere uguali e otteniamo così
i (t ) = C ⋅
dV
dt
cioè
i (t ) = C ⋅ V ' (t )
che è la relazione esistente tra l'intensità i della corrente di carica o di
scarica di un condensatore di capacità C e la tensione V di ai capi della stessa.
3. FORZA E ELETTROMOTRICE INDOTTA
Ricordiamo dalla fisica che, dato un circuito elettrico chiuso di superficie S,
se a esso è concatenato un flusso Φ del campo di induzione magnetica B, variabile
con il tempo t secondo una relazione Φ=Φ(t), nel circuito si produce una f.e.m.
(forza elettromotrice) media, Em, definita da
Em = −
Φ(t + ∆t ) − Φ(t )
∆t
e una f.e.m. (forza elettromotrice) istantanea
e=−
dΦ(t )
dt
→ e = −Φ ' (t )
È evidente che quest'ultima formula, che dà il valore di e, si ottiene dalla
precedente, che dà il valore di Em, passando al limite per Δt tendente a zero
Esempio
Consideriamo una spia di superficie S immersa in un campo uniforme di
induzione magnetica B , libera di ruotare attorno a un asse perpendicolare alle
linee di forza e sia α l'angolo formato dal versore n , normale alla spira, con il
vettore campo B . Se la velocità angolare ω di rotazione della spira è costante,
al tempo t si ha α = ωt ed il flusso del campo B concatenato con la spira,
all'istante t, è espresso da
Φ (t ) = BS cos ωt
Il valore della forza elettromotrice indotta nella spira all'istante t è dato da
dΦ (t )
e=−
= BS sin ωt
dt
ed è quindi una f.e.m. ad andamento sinusoidale.
4. FORZA ELETTROMOTRICE AUTOINDOTTA
In generale è possibile associare ad ogni circuito elettrico una grandezza L,
detta coefficiente di autoinduzione o induttanza, che lega i valori istantanei del
flusso Φ(t), concatenato con il circuito, con quello della corrente i(t), che
attraversa il circuito, secondo la relazione
Φ(t)= L·i(t)
(7)
Se nell'intervallo di tempo (t ; t + ∆t ) la corrente subisce la variazione
∆i = i(t + ∆t ) − i (t ) , si produce una corrispondente variazione del flusso che, per la
(7) e supponendo L costante del tempo, è:
∆Φ = Φ(t + ∆t ) − Φ(t ) = L ⋅ i(t + ∆t ) − L ⋅ i(t ) = L ⋅ [i (t + ∆t ) − i(t )] = L ⋅ ∆i .
Nel circuito si genera quindi una forza elettromagnetica autoindotta che
all'istante t è data da
∆Φ
L∆i
∆i
di
e = − lim
= − lim
= − L lim
= −L
∆t → 0 ∆t
∆t → 0 ∆t
∆t → 0 ∆t
dt