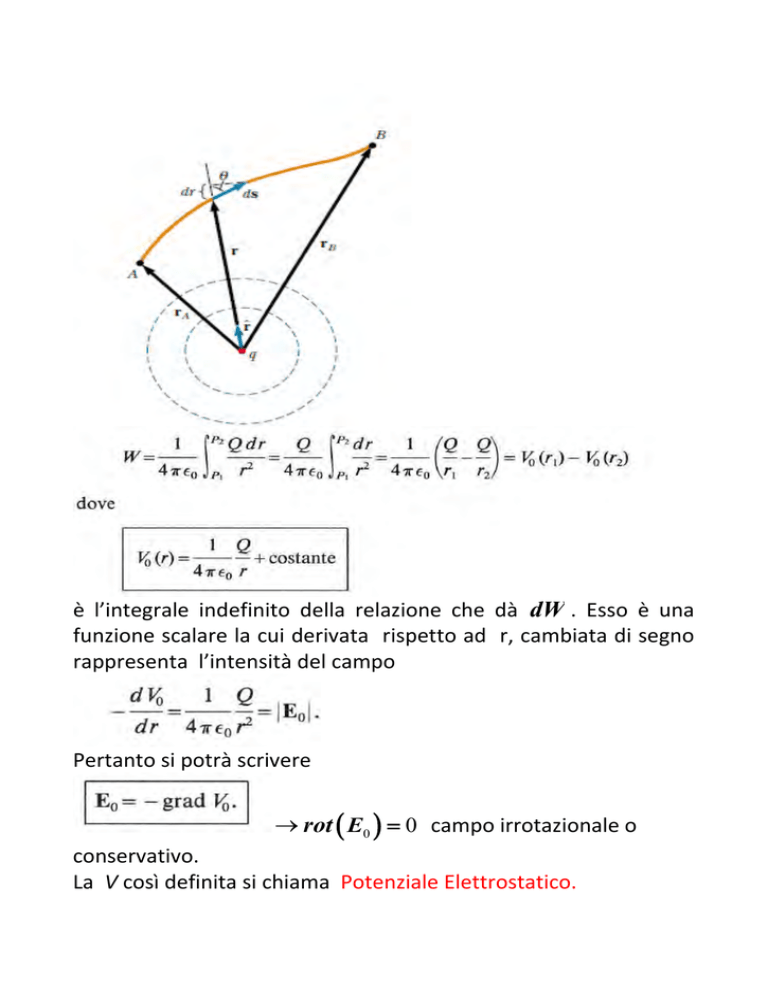
è l’integrale indefinito della relazione che dà dW . Esso è una
funzione scalare la cui derivata rispetto ad r, cambiata di segno
rappresenta l’intensità del campo
Pertanto si potrà scrivere
rot E0 0 campo irrotazionale o
conservativo.
La V così definita si chiama Potenziale Elettrostatico.
La sua derivata rispetto ad una direzione qualsiasi fornisce
la
componente in quella direzione del campo elettrico E0
cambiata di segno.
Il segno - deriva dal fatto che il campo elettrico è stato definito
come un vettore che va dalla carica +Q (che genera il campo)
verso l’esterno: vale a dire vettore rivolto dai punti in cui il
potenziale è maggiore verso i punti in cui il potenziale è minore,
mentre il vettore grad (V0 ) ha verso opposto.
Assumendo che sia nulla la costante nella
1 Q
V0 ( r )
costante
4 0 r
Avremo
1 Q
V0 ( r )
4 0 r
In tal modo per r il potenziale si annulla e potremo
affermare che il lavoro fatto dal campo E0 quando la carica
unitaria si sposta da un punto P in cui il potenziale ha il valore
V0 ( r ) , fino all’infinito ( dove il potenziale è nullo) è uguale a:
Se invece di una carica unitaria si sposta una carica q dal punto P 1
al punto P2, il lavoro fatto dalla forza
F=E0q sarà
Che per r2 si riduce a
Che ci fornisce l’energia potenziale della carica q quando essa è
posta nel punto in cui il potenziale ha il valore V0 ( r1 ) .
Dalla particolare scelta della costante d’integrazione segue che
se la carica che genera il campo è positiva, il potenziale V0 ( r ) è
pure positivo. Inoltre data una carica positiva che genera il
campo, l’energia potenziale di una qualsiasi altra carica risulta
positiva o negativa a seconda del suo segno.
L’unità di misura del potenziale ossia anche della differenza di
potenziale si chiama volt ed è legata alle suddette unità dalla
relazione
W
V0 ( r1 ) V0 ( r2 )
q
1 joule
newton.metro
1volt
1coulomb
coulomb
Energia Potenziale di una carica
Il lavoro della forza di Coulomb è
indipendente dal cammino.
dl
•Si
può associare energia potenziale
U (r ) alla carica q0 in ogni punto r.
→
dW = q0 E ⋅ d l
→
dU = −dW = −q0 E ⋅ d l
∆U= U ( r ) − U (i )
0
→
r
→
r
== −
−∫∫i qq00EEd⋅ dl l
∞
i
i è il punto di rif.
dl
→
i è spesso
all' (∞)
dW = q0 E ⋅ d l
→
dU = −dW = −q0 E ⋅ d l
a
∆U= U (b) − U ( a )
→
bb
== −−∫ FFd⋅ dl l
∫
aa
b
mg
Gravità
−mg ∆l
qE
Coulomb
− qE ∆l
(con g, E uniformi)
Il lavoro fatto da
<gravità/Coulomb> è la
diminuzione dell'energia pot.
Energia Potenziale Elettrostatica
Per un sistema (rispetto a ∞) è il lavoro necessario per portare
le cariche fino all'infinito o il lavoro esterno necessario per
arrivare dall'∞ alle posizioni attuali
q1
kq1q2 kq1q3 kq2 q3
U=
W= +
+
r13
r12
r
r
r
q2
r23
q3
12
13
23
kq3 kq1
kq1 kq2
1 kq2 kq3
=
+
+
+
q1
+ q2
+ q3
2 r12
r13
r
r
r
r
12
23
23
13
1
=
( q1V1 + q2V2 + q3V3 )
2
n
1
Genericamente per n cariche: U = ∑ qV
i i
2 i =1
Il fattore 1/2 c'è per compensare il doppio
conteggio di energia potenziale per ogni coppia di cariche.
Da ∞
U (r ) =
= −
∫∫
→
qq00EE ⋅ dl
dl
∞→
∞ →PP
q0 q
= − ∫ k 2 r dl
l
∞→ P
q0 q
= − ∫ k 2 dl
∞
l
r
r
q0 q
q0 q
= =
k
k
r
l ∞
= energia pot. della configurazione di
q e q0.
q1q2
k
d
q1q3
k
d
q2 q4
k
d
q3q4
k
d
k
q2 q3
2d
k
q1q4
2d












