Circuitazione di un campo vettoriale
1-4
La circuitazione di un campo vettoriale lungo una linea chiusa orientata
è definita dal prodotto scalare:
!
!
!
CΓ ( v ) = ∑ v i ⋅ Δγ i = ∑ v i Δγ i cosα i
dove Γ è un percorso chiuso e γi è uno dei generici tratti rettilinei
mediante i quali si può pensare composto il percorso per poter
calcolare il prodotto scalare.
Circuitazione di un campo vettoriale
Per cogliere il significato fisico della circuitazione, applichiamone la definizione matematica ad
un tubo di flusso in condizioni di stazionarietà (flusso laminare) di un fluido.
Consideriamo un percorso ABCD rettangolare, ma teniamo presente che il risultato si può
generalizzare per ogni tipo di percorso chiuso.
D
C
Γ
v
A
B
Gli angoli che il vettore velocità v forma con i quattro tratti con cui suddividiamo il percorso
sono: 0° con AB, 90° con BC, 180° con CD, 270° con DA. Ricordando i valori del coseno per
questi angoli si ottiene, per la somma di tutti i prodotti scalari, un valore nullo:
CΓ (v) = ∑ v i ⋅ Δγ i = vABcos0 + vBCcos90° + vCDcos180° + vDAcos270° = vAB − vCD = 0
Ovvero:
CΓ( v ) = 0
2-4
3-4
Circuitazione di un campo vettoriale
E se applicassimo la formula della circuitazione ad un fluido che presenta un moto vorticoso?
Γ
v del fluido
Elemento di
Γ
Non diamo importanza al fatto che
nella realtà la velocità dei venti di un ciclone non sia costante in tutti i punti
del percorso circolare, il nostro è solo
un esempio. L’elemento importante è il
valore della circuitazione che si ottiene
in condizioni vorticose o, in generale,
non stazionarie.
Gli angoli che il vettore velocità v forma con gli elementi rettilinei in cui il percorso viene suddiviso sono sempre di 0°, pertanto gli addendi della somma di tutti i prodotti scalari avranno
sempre lo stesso segno algebrico, quindi la circuitazione non sarà nulla:
CΓ(v) ≠ 0
4-4
Circuitazione di un campo vettoriale
Circuitazione di un campo vettoriale
Applichiamo questa definizione matematica ad un tubo di flusso in condizioni di stazionarietà
(flusso laminare) di un fluido.
Consideriamo un percorso ABCD rettangolare, ma il risultato si può generalizzare per ogni
tipo di percorso chiuso.
D
Circuitazione di un campo vettoriale
E se applichiamo la formula della circuitazione ad un fluido che presenta un moto vorticoso?
C
Γ
v
A
B
v del fluido
Elemento di Γ
Γ
Non diamo importanza al fatto che
nella realtà la velocità dei venti di un ciclone non sia costante in tutti i punti
del percorso circolare, il nostro è solo
un esempio. L’elemento importante è
che in condizioni vorticose o, in generale, non stazionarie la circuitazione
non è nulla.
Gli angoli che il vettore velocità v forma con i quattro tratti con cui suddividiamo il percorso
sono: 0° con AB, 90° con BC, 180° con CD, 270° con DA, ricordando i valori del coseno per
questi angoli si ottiene un valore nullo:
r
r r
CC
(v)==∑
⋅ Δγi =i =vABcos0
vABcos0++vBCcos90°
vBCcos90°++vCDcos180°
vCDcos180°++vDAcos270°
vDAcos270° = vAB − vCD = 0
Γ (v)
∑vvi ⋅i Δγ
Γ
Ovvero:
CΓ(v) = 0
Gli angoli che il vettore velocità v forma gli elementi rettilinei con cui il percorso viene
suddiviso sono sempre di 0°, pertanto gli addendi della somma di tutti i prodotti scalari
avranno sempre lo stesso segno algebrico, pertanto la circuitazione non sarà nulla.
CΓ(v) ≠ 0
Il calcolo della circuitazione di un campo vettoriale ci
permette di determinare se siamo in presenza di un
flusso laminare o turbolento.
1-1
Lavoro e circuitazione di un campo elettrostatico
Avete visto che il lavoro di E vale:
WΓ E = ∑ qE i ⋅ ΔS i = ∑ qE i ΔS i cosα i
( )
ΔSj
Γ
ΔSi
E
Applicando ad E la definizione di circuitazione troveremmo:
CΓ E = ∑ E i ⋅ ΔS i = ∑ E i ΔS i cosα i
( )
W e C si corrispondono a meno della carica di prova q: a meno di una
costante. Quindi tutte le considerazione svolte su W valgono anche per la
circuitazione. Ma se W ci dice qualcosa sulle proprietà energetiche di E in
relazione ad una carica esploratrice q, C ci dice qualcosa intrinseco ad E
stesso, in particolare che il campo elettrostatico è irrotazionale e conservativo.
CΓ( E )=0 per ogni percorso chiuso Γ implica la possibilità di definire una
funzione scalare, detta potenziale V, di cui avete già parlato e che dà del
campo una rappresentazione energetica.
CΓ( E )=0 per ogni Γ chiusa costituisce la terza equazione di
Maxwell per il campo elettrostatico.
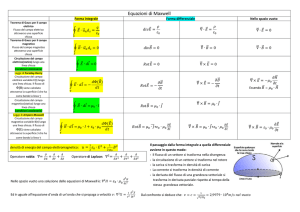
Equazioni di Maxwell per il campo elettrostatico
1)
Σq
Φ Ω (E) =
ε
Il flusso del campo elettrico, attraverso una superficie chiusa Ω, è pari alla somma algebrica
delle cariche in essa contenute fratto la costante
dielettrica del mezzo in cui si trovano le cariche.
Equivale all’esistenza del monopolo elettrico. Significa che esiste la singola carica elettrica
(positiva o negativa). Significa che le linee di forza del campo elettrico possono anche essere
delle semirette (con origine e senza fine) o linee aperte.
3)
CΓ (E) = 0
Lungo un qualunque percorso chiuso Γ la circuitazione del campo elettrostatico è nulla.
Esprime matematicamente le proprietà del campo elettrostatico di essere:
1) conservativo (il lavoro compiuto dal campo elettrostatico non dipende dal percorso, ma dal punto iniziale e finale del percorso o, analogamente, che lungo un qualunque percorso chiuso il lavoro è nullo.)
2) irrotazionale.
Significa che per conoscere il campo elettrico dal punto di vista energetico può essere
definita una funzione dipendente soltanto dalla posizione (il potenziale) e il lavoro
compiuto su una carica può essere conosciuto tramite una funzione della sola posizione detta energia potenziale.
1-1