Circuitazione del campo elettrostatico

Enunciato
Per i fenomeni stazionari la circuitazione del campo elettrico è nulla, cioè il campo elettrico è
conservativo.
In sintesi:

C E 0

Dimostrazione
Primo passo
Per dimostrare la conservatività del campo elettrico, dimostriamo prima quella della forza di
Coulomb, cioè consideriamo una carica puntiforme di prova q soggetta all’azione di una carica
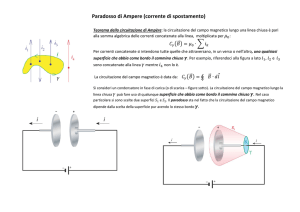
sorgente puntiforme Q. Verifichiamo che il lavoro fatto dalla
forza di Coulomb quando la carica q si sposta da un punto A ad
B

un punto B non dipende dal percorso. Per la dimostrazione
F
procediamo in due modi, il primo un po’ “artigianale”, il A

secondo rigoroso, con l’utilizzo del calcolo integrale.“
Dimostrazione “artigianale”:
N 
 N  
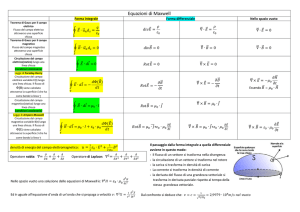
L AB   Fi  ri   Fi ri cos  i osservando il disegno
H
i 1
i 1

 i Pi+1
ri cos  i  Pi P i 1 cos  i  Pi H  ri  ri 1  ri ,
cioè
la
Pi
variazione della distanza tra le due cariche. La forza di Coulomb
passando da Pi a Pi+1 varia, poiché varia la distanza tra le due
cariche, è possibile però considerarne un valore medio
utilizzando per la distanza la media geometrica ( r  ri 1  ri )

Qq
1

quindi F 
Sostituendo nella sommatoria si
40 ri ri 1
ottiene una somma telescopica:
N Qq
N Qq 1
1
1
Qq 1 1 1 1 1 1
1
L AB  

(ri 1  ri )  
( 
)
(       ...  )
ri 1
40 rA r1 r1 r2 r2 r3
rB
i 1 40 ri ri 1
i 1 40 ri
Ciò che rimane è L AB 
Qq  1
1
   , cioè un’espressione che non dipende dal percorso, come
40  rA rB 
volevamo dimostrare.
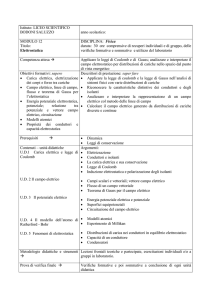
H
Dimostrazione rigorosa:
L AB
 
 
  F  dr   F dr cos  osservando il disegno
AB
P1

P2
AB

dr cos   P1 P2 cos   P1 H  dr , cioè la variazione della
distanza tra le due cariche. Sostituendo nell’integrale anche
l’espressione della forza di Coulomb si ottiene un integrale
Circuitazione del campo elettrostatico
1
definito, al quale possiamo mettere gli estremi rA ed rB.
r
Qq rB 1
Qq  1  B
Qq  1
1 
  
dr






2
40 rA r 2
40  r  rA 40  rA rB 
rA 40 r
cioè un’espressione che non dipende dal percorso, come volevamo dimostrare.
rB
L AB  
Qq
dr 
Secondo passo
Poiché, come abbiamo dimostrato, la forza di Coulomb è conservativa, il lavoro da essa compiuto
su un qualunque percorso chiuso è nullo, cioè la circuitazione della forza di Coulomb è sempre

nulla C F  0
 
Terzo passo

 F
Ricordando il legame tra forza e campo E 
e la linearità della circuitazione si ottiene che per il
q

 C(F ) 0
campo generato da una sorgente puntiforme Q: C E 
 0
q
q

Quarto passo
Per considerare il caso generale, cioè il campo generato da N sorgenti, ricordiamo il principio di
sovrapposizione degli effetti, cioè il campo elettrico è la somma vettoriale dei campi che ciascuna
 


sorgente genererebbe se fosse da sola: E  E1  E2  ....  E N , essendo la circuitazione un
operatore lineare (cioè la circuitazione di una somma è uguale alla somma delle circuitazioni), si
potrà scrivere:




C( E)  C( E1 )  C( E2 )  ....  C( E N )  0 . Cioè la tesi
Circuitazione del campo elettrostatico
2