ESERCIZI E DOMANDE SULLA PARTE DI STATISTICA INFERENZIALE.
DOMANDE
1. Descrivi brevemente di cosa si occupa la statistica inferenziale, quali sono le fasi di uno studio
statistico, in quali di esse si utilizzano metodi statistici e in quali metodi probabilistici.
2. Spiega il significato dei seguenti termini: parametro, stimatore, stima.
3. Descrivi gli stimatori che si utilizzano per ottenere una stima per intervallo della media o della
proporzione di una popolazione.
4. Cosa significa che uno stimatore è corretto? Fai un esempio di stimatore corretto e un esempio di
stimatore non corretto.
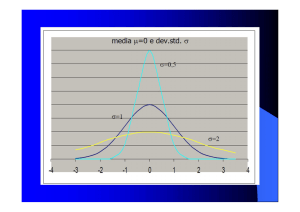
5. Enuncia il teorema limite centrale, e spiega qual è la sua importanza nella stima dei parametri di una
popolazione a partire da un campione.
6. Definisci la variabile casuale “varianza campionaria” . Cosa significa che è uno stimatore non
corretto? Come si fa ad ottenere la varianza campionaria corretta?
7. Scrivi le relazioni che intercorrono tra la varianza della popolazione, la varianza della media
campionaria e la media della varianza campionaria. La media della varianza campionaria è maggiore
o minore della varianza della popolazione?
7. Definisci la variabile casuale “frequenza campionaria”. Qual è il parametro della popolazione che si
stima con la frequenza campionaria? E’ uno stimatore corretto di tale parametro?
8. Cos’è lo spazio campionario? Da quanti elementi è formato lo spazio campionario di dimensione n,
in caso di estrazione bernoulliana, su una popolazione di N individui?
9. Una popolazione è composta da 1000 unità. Sapendo che la distribuzione della varianza campionaria
S2 ha valore medio 17 e che è stato effettuato un campionamento bernoulliano con n = 35,
determina la varianza della popolazione.
10.
11. Cos’è un intervallo di confidenza per una media o una proporzione? Se il livello di confidenza
aumenta (e quindi l’intervallo di confidenza diventa più ampio) la stima della media diventa più
precisa?
Da cosa dipende l’intervallo di confidenza?
Cosa significa stimare una media con grado di fiducia del 70%?
STIME PUNTUALI E ERRORE STANDARD
1. Si vuole stimare il consumo medio giornaliero di zucchero, il consumo totale della popolazione e la
percentuale di persone che usa dolcificanti, in una popolazione di 4000 individui. Si estrae un campione
bernoulliano di 150 persone, e si rileva che la media del campione è di 30 g, con una deviazione
standard di 12 g. Si rileva inoltre che il numero delle persone che usa dolcificanti è 48. Determinare la
stima puntuale dei parametri della popolazione, con i relativi errori standard.
2.
3
4. Una macchina confeziona ogni giorno 800 sacchetti di caramelle, e un campione casuale di 50 sacchetti
ha rivelato un peso medio per sacchetto di 405 g con una deviazione standard di 12 g.
Determinare:
a) il peso medio di un sacchetto della produzione, con l’errore standard, supponendo il campionamento
bernoulliano.
b) il peso totale delle caramelle prodotte, con il relativo errore standard
c) quale deve essere la numerosità del campione nel caso si voglia ridurre l’errore del 30%.
STIME PER INTERVALLO
1.
2.
3.
4.
5.
6.
7.
8. Una macchina produce barattoli di caffè del peso dichiarato di 250g. Il peso reale è una variabile
aleatoria normale di media 250g e deviazione standard 5g. le confezioni il cui peso reale si scosta per più
del 4% da quello dichiarato vanno scartate. Qual è la percentuale di confezioni da scartare?
9. Il processo di produzione di un’azienda, quando funziona normalmente, dà luogo a una percentuale di
pezzi difettosi del 5%. Al fine di eseguire un controllo qualità viene estratto un campione bernoulliano
di 150 pezzi. 11 di essi risultano difettosi. La produzione può essere ritenuta in controllo, a un livello di
confidenza del 99%?
Ad un controllo successivo, viene estratto un campione di 200 pezzi, 18 dei quali risultano difettosi. La
produzione può essere ritenuta in controllo, ad un livello di confidenza del 95%?
10. Un’azienda produce sfere metalliche il cui diametro medio è di 2 cm, con una deviazione standard di
0,15 cm. Al fine di eseguire un controllo di qualità viene estratto un campione casuale bernoulliano di 50
sferette. Entro quali limiti deve essere contenuto il diametro medio delle sferette del campione, perché
la produzione si possa ritenere in controllo, a livello di confidenza del 95%?
11.