L` amperometro dello strumento universale

L’ amperometro dello strumento universale
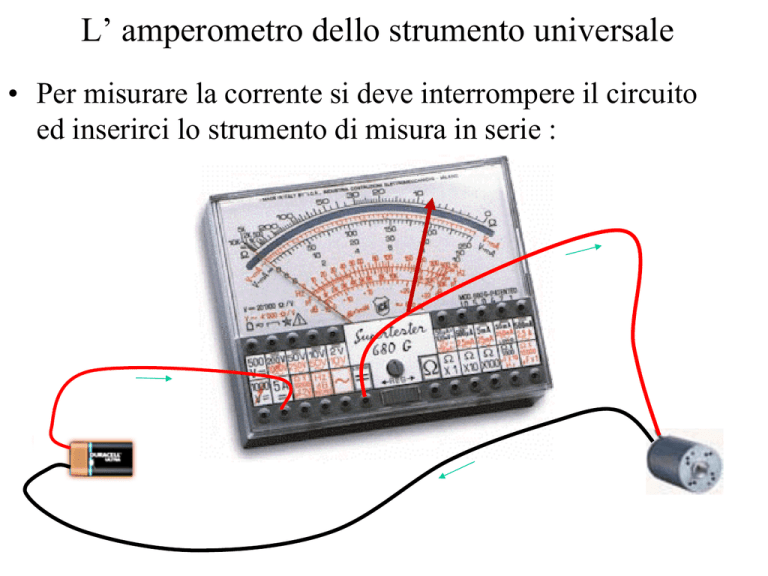
• Per misurare la corrente si deve interrompere il circuito
ed inserirci lo strumento di misura in serie :
L’ amperometro dello strumento universale
Strumento Universale
F.S.=40A , RA=1600
+
0.064 0.576 5.76
57.6
576
5760
720
=
5A
500mA
Batteria
+
+
V
-
50mA
i
5mA
500A
Motore

R
-
50A
L’ amperometro dello strumento universale
• Per ottenere che lo strumento vada a fondo scala quando misura
una corrente di 5A, si deve fare in modo che la corrente si partisca
in IA=40 A nell’amperometro, e il resto nello shunt.
• Considerando il partitore di corrente formato da una parte dallo
shunt RS relativo alla scala 5A, e dall’altra parte dall’amperometro
con in serie tutte le altre resistenze di shunt, che totalizzano Rserie ,
si vede che I ( R  R )  I R 
A
A
serie
S
S
RS
40A
IA
 
 8.00 106
( RA  Rserie ) I S 5 A  40A
• In effetti, se RA=1600, Rserie=(5760+576+57.6+5.76+0.576) e
RS=0.064, si ottiene proprio
R
S
( RA  Rserie )
 8.00 106
L’ amperometro dello strumento universale
Strumento Universale
F.S.=40A , RA=1600
+
iA
0.064 0.576 5.76
iS
=
5A
500mA
50mA
5mA
500A
Motore
+

5760
720
Batteria
+
V
-
576
iA
i
i
57.6
i
i
R
-
i
50A
L’ amperometro dello strumento universale
Strumento Universale
F.S.=40A , RA=1600
+
iA
0.064 0.576 5.76
iS
57.6
iA
=
5A
500mA
50mA
Batteria
5mA
500A
Motore
+

5760
720
i
i
+
V
-
576
i
i
R
-
i
50A
Concetto Importante
• L’ amperometro si
inserisce sempre IN
SERIE al circuito di cui
si vuole misurare la
corrente.
• L’ amperometro non si
inserisce MAI IN
PARALLELO al
circuito di cui si deve
misurare la corrente.
Batteria
+
V
-

+ A
R
-
Batteria
Motore
+
+
V
-
Motore

A
-
R
Concetto Importante
• L’ amperometro si
inserisce sempre IN
SERIE al circuito di cui
si vuole misurare la
corrente.
• L’ amperometro non si
inserisce MAI IN
PARALLELO al
circuito di cui si deve
misurare la corrente.
• (bassa R!)
Batteria
+
V
-

+ A
R
-
Batteria
Motore
+
+
V
-
Motore

A
-
R
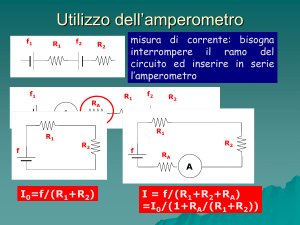
Perturbazione introdotta dall’ amperometro.
• L’ inserimento dell’ amperometro aumenta la resistenza totale del
circuito in cui è inserito, quindi la corrente misurata è leggermente
inferiore a quella imperturbata. Possiamo calcolare quanto.
• Tra i due punti del circuito in cui operiamo l’ interruzione, il circuito
in misura può essere rappresentato dal suo equivalente secondo
Thevenin: Circuito
Circuito
IA=Vo/(RA+Ro)
equivalente I=Vo/Ro
equivalente
+
+
Ro
Ro
+
+
RA
Vo
Vo
Vo
Amperometro
Vo
Ro
I
IA 


R
R
Ro  R A
1 A
1 A
Ro
Ro
Perturbazione introdotta dall’ amperometro.
• L’ entità della correzione da apportare alla misura IA per ottenere I
dipende dal rapporto RA/Ro. RA è scritto nelle specifiche dell’
amperometro, Ro si può valutare o misurare.
• Vale la pena di apportare la correzione se l’ errore
I  IA
RA

IA
Ro
• è maggiore dell’ errore percentuale commesso nella lettura di IA,
sommato all’ errore di calibrazione.
• Il valore di RA dipende ovviamente dal particolare shunt utilizzato,
e quindi dal fondo scala scelto.
• Questo fatto può essere utilizzato a nostro vantaggio per eliminare
Ro dalla valutazione di I, eseguendo la misura con due fondo-scala
diversi (con diverse RA, ambedue note) ed ottenendo quindi un
sistema con due equazioni e due incognite.
Il Voltmetro analogico
• Il voltmetro è uno strumento che misura la differenza
di potenziale mediante la misura dell’ intensità di
corrente che scorre in un resistore di resistenza nota.
• Il voltmetro è quindi uno strumento a bobina mobile
(come l’ amperometro), ma stavolta con una
ELEVATA resistenza interna RV , in modo che
perturbi poco la misura:
- A +
Amperometro
- A +
RV
Voltmetro
Il voltmetro dello strumento universale
F.S.=40A , RA=1600
+
0.064 0.576 5.76
57.6
576
5760
720
5A
500mA
50mA
32220
160k 800k
= 100mV 2V
10V
50V
500A 50A
5mA
6520
5M
6M
200V
10M
500V
1000V
Il voltmetro dello strumento universale
• Esempio: misurare la tensione ai capi della batteria che
alimenta un motorino elettrico (durante il
funzionamento):
• Schema equivalente:
Batteria
+
+
V
-
Motore
i

VR
-
R
Il voltmetro dello strumento universale
• Per misurare la tensione si deve inserire lo strumento di
misura in parallelo :
Il voltmetro dello strumento universale
• Per misurare la tensione si deve inserire lo strumento di
misura in parallelo :
Perturbazione introdotta dal Voltmetro
• L’ inserimento del Voltmetro riduce leggermente
la tensione ai capi del motore, perchè una piccola
parte della corrente originale passa nel voltmetro.
Batteria
+
+
V
-
Motore
i

VR
-
RV
R
Perturbazione introdotta dal Voltmetro
• Come al solito: si schematizza il circuito in misura con il suo
equivalente secondo Thevenin.
Circuito
equivalente
Circuito
equivalente
+
+
Vo
-
Ro
+
V=Vo
-
Voltmetro
+
Vo
-
Ro
RV
-
Vo
IV 
Ro  RV
 Ro
RV
1
 Vo
 Vo  VV 1 
VV  IV RV  Vo
Ro
Ro  RV
 RV
1
RV



Perturbazione introdotta dal Voltmetro
•
•
•
 Ro
Vo  VV 1 
 RV



L’ entità della correzione dipende dal rapporto Ro/ RV . La correzione è
trascurabile se (Vv-Vo)/Vv è minore degli errori di lettura e di calibrazione.
Il valore di RV si valuta a partire dalla corrente di fondo scala dell’ amperometro
che c’è all’ interno del voltmetro.
Per lo strumento universale a nostra disposizione, la corrente di fondo scala è di
50A. Per la legge di Ohm:
RV
1

I FS VFS
•
Quindi abbiamo una resistenza interna del Voltmetro di 20000/VFS. Ad
esempio
– per il fondo scala di 50V, la resistenza RV vale 20000/VFS x 50 VFS=1M.
– per il fondo scala di 100mV, la resistenza RV vale 20000/VFS x 0.1 VFS=2k.
Voltmetri e Amperometri Digitali Elettronici
• Si può migliorare lo strumento di misura di correnti e tensioni in
due modi:
– Diminuendo le perturbazioni che esso introduce nel circuito
– Costruendo circuiti che convertono il risultato della misura in
forma digitale, in modo da
• Usare una visualizzazione numerica, eliminando l’ errore di
lettura sulla scala graduata
• poterlo acquisire su un computer per una successiva
elaborazione.
Voltmetri e Amperometri Digitali Elettronici
•
•
•
Le perturbazioni introdotte dallo strumento analogico sono dovute alla resistenza
relativamente bassa della bobina mobile (è un avvolgimento di filo) ed alla
corrente relativamente alta necessaria a produrre la coppia necessaria per muovere
l’ equipaggio mobile.
Si possono utilizzare dei circuiti amplificatori, inserendoli tra il circuito sotto
misura e l’ amperometro, in modo da produrre una corrente nell’ amperometro
amplificata di un fattore G>1 rispetto alla corrente estratta dal circuito in esame.
All’ interno di questi amplificatori si utilizzano Transistor a Effetto di Campo
(FET, field effect transistor), che permettono di generare correnti rilevanti
estraendo una corrente trascurabile (fA=10-15A) dal circuito in esame.
+
-
Amplificatore
differenziale
V
Voltmetri e Amperometri Digitali Elettronici
•
•
•
Le perturbazioni introdotte dallo strumento analogico sono dovute alla resistenza
relativamente bassa della bobina mobile (è un avvolgimento di filo) ed alla
corrente relativamente alta necessaria a produrre la coppia necessaria per muovere
l’ equipaggio mobile.
Si possono utilizzare dei circuiti amplificatori, inserendoli tra il circuito sotto
misura e l’ amperometro, in modo da produrre una corrente nell’ amperometro
amplificata di un fattore G>1 rispetto alla corrente estratta dal circuito in esame.
All’ interno di questi amplificatori si utilizzano Transistor a Effetto di Campo
(FET, field effect transistor), che permettono di generare correnti rilevanti
estraendo una corrente trascurabile (fA=10-15A) dal circuito in esame.
+
+
Vo
-
+
Ro
1015
-
Circuito in esame
(Equivalente secondo Thevenin)
Voltmetro elettronico
V
Voltmetri e Amperometri Digitali Elettronici
• La tensione in uscita dal voltmetro può essere convertita in un
numero digitale utilizzando un apposito Convertitore Analogico
Digitale (ADC = analog to digital converter).
• Si tratta di un circuito che converte una tensione in ingresso in un
insieme di N livelli di tensione in uscita, ciascuno dei quali
rappresenta un bit della rappresentazione binaria {Bn,n=0,N-1} del
valore della tensione (Bn=0 o 1 a seconda che il livello di tensione
sull’ n-ma linea sia 0 o 5V).
V  n 0 Bn 2 n
N 1
BN-1
BN-2
+
V
1015
-
ADC
B1
B0
Voltmetri e Amperometri Digitali Elettronici
• La tensione in uscita dal voltmetro può essere convertita in un
numero digitale utilizzando un apposito Convertitore Analogico
Digitale (ADC = analog to digital converter).
• Si tratta di un circuito che converte una tensione in ingresso in un
insieme di N livelli di tensione in uscita, ciascuno dei quali
rappresenta un bit della rappresentazione binaria {Bn,n=0,N-1} del
valore della tensione (Bn=0 o 1 a seconda che il livello di tensione
sull’ n-ma linea sia 0 o 5V).
V  n 0 Bn 2 n
N 1
BN-1
Apparato di
Visualizzazione
(display
o
computer)
+
V
1015
ADC
B0
Convertitore Digitale Analogico - 1
bit1
22Ro
21Ro
bit(N-1)
bit0
23Ro
bit(N-2)
2N-2Ro
bit(N-3)
2N-1Ro
bit(N-4)
• Consideriamo una rete fatta di N resistenze con valori che vanno da
Ro a 2N-1Ro.
• Usando i deviatori, ciascuna delle resistenze può essere connessa a
V oppure no, a seconda che il relativo bit sia 1 o 0.
Ro
+
V
LSB
MSB
Convertitore Digitale Analogico - 1
• Quando si accende il bit n, nell’ amperometro scorre una corrente
i=V/ 2N-n-1Ro
bit0
bit1
+
V
-
i
LSB
2N-n-1Ro 22Ro
bit n
21Ro
Ro
bit(N-1)
2N-2Ro
bit(N-2)
2N-1Ro
i
MSB
• Se si accendono i bit n1, n2, n3, nell’ amperometro scorre una corrente
i=V(1/ 2N-n1-1Ro+ 1/ 2N-n2-1Ro+ 1/2N-n3-1Ro)
• Ma la corrente di ciascun bit è un multiplo della corrente del bit più
piccolo io=V/ 2N-1Ro
• Quindi l’ LSB produce una corrente io, il successivo 2io, il successivo
4io e così via fino a 2N-1io per il MSB.
• Si può approssimare una i qualsiasi con la combinazione binaria dei
N 1
n
bit opportuni (quantizzando la i con passo io). i  i
B 2
2N-n1-1Ro
bit0
+
V
-
LSB=Least Significant Bit
2N-n2-1Ro
bit n2

n 0
n
2N-n3-1Ro
bit n3
bit(N-1)
2N-1Ro
bit n1
o
Ro
MSB=Most…
Convertitore Digitale- Analogico
• Un convertitore DigitaleAnalogico (DAC, digital to
analog converter) a N bit è
un circuito con N ingressi
ed una uscita
• In ingresso ci sono le N
tensioni che rappresentano
il numero binario d’
ingresso Bn: Vi=0 o V a
seconda che Bi=0 o 1
• In uscita c’è la corrente
proporzionale al numero d’
N 1
ingresso:
n
i  io n 0 Bn 2
MSB
DAC
LSB
i
Convertitore Digitale- Analogico
MSB
0011010010111
0011001010011
0011010010010
0011010010101
0011011101010
0011010001010
0011001010111
0011011101011
Bi(tk)
t1 t2 t3 t4 … tn tn+1 tn+2
Ingresso: sequenza
di numeri binari
LSB
(campionamento)
i
DAC
i
t1 t2 t3 t4 … tn tn+1
Uscita: corrente
variabile nel tempo
(campionamento)
Convertitore Digitale- Analogico
• L’ applicazione tipica è il riproduttore di musica digitale (CD):
MSB
i
0011010010111
0011001010011
0011010010010
0011010010101
0011011101010
0011010001010
0011001010111
0011011101011
Bi(tk)
DAC
t1 t2 t3 t4 … tn tn+1 tn+2
i
t1 t2 t3 t4 … tn tn+1
LSB
Convertitore Digitale Analogico - 1
• Il difetto di questo circuito è che Ro deve essere molto maggiore
della resistenza interna dell’ amperometro (v. Ipotesi fatta su Io e In),
che già da sola può essere 1k).
• Allora per 16 bit (216=65536 livelli di corrente) la resistenza più
grande deve essere >>215ke contemporaneamente precisa entro
1k. Non si fa !
+
V
LSB=Least Significant Bit
2n2Ro
bit n2
2n3Ro
bit n3
bit(N-1)
bit0
o
2n1Ro
bit n1
2N-1R
Ro
MSB=Most…
Convertitore Digitale Analogico - 2
• Consideriamo invece una rete fatta di resistenze R e 2R come sotto.
• Usando i deviatori, ciascuna delle resistenze 2R può essere
connessa a 0 oppure a V a seconda che il relativo bit sia 0 o 1.
V
+
2R
2R
bit0
bit1
R
2R
R
2R
R
2R
2R
bit(N-1)
2R
R
bit(N-2)
R
2R
A
• Quando si connette a +V uno qualsiasi dei bit, la corrente attraverso
di esso si divide in parti uguali nei due rami del circuito.
• Infatti:
+
V
-
2R
R
R
2R
2R 2R
2R
R
2R
R
R
2R
R
2R
2R
2R
A
• Quando si connette a +V uno qualsiasi dei bit, la corrente attraverso
di esso si divide in parti uguali nei due rami del circuito.
• Infatti:
+
V
-
2R
R
R
2R
2R
2R 2R
2R
R
2R
R
R
2R
R
2R
2R
2R
A
• Quando si connette a +V uno qualsiasi dei bit, la corrente attraverso
di esso si divide in parti uguali nei due rami del circuito.
• Infatti:
+
V
-
2R
R
R
2R
R
2R
2R
R
2R
2R 2R
2R
R
2R
R
2R
2R
2R
A
• Quando si connette a +V uno qualsiasi dei bit, la corrente attraverso
di esso si divide in parti uguali nei due rami del circuito.
• Infatti:
+
V
-
2R
R
R
2R
R
R
2R
R
2R
2R 2R
2R
2R
R
2R
2R
2R
A
• Quando si connette a +V uno qualsiasi dei bit, la corrente attraverso
di esso si divide in parti uguali nei due rami del circuito.
• Infatti:
+
V
-
i
i/2
2R
• Inoltre i=V/3R
2R
i/2
2R
• Inoltre la corrente in ciascuna resistenza R è metà di quella nella
resistenza R precedente. Quindi se si accende il bit n, nell’
amperometro scorre una corrente i/2N-n. Quindi le correnti sono tutte
multiple della corrente minima (bit0) che vale i/2N
+
V
i
2R
i/2
i/22
i/2N-n-1 i/2N-n
R
R
R
2R
2R
2R
R
2R
2R 2R
2R 2R
bit0
bit1
bit(n-1)
LSB=Least Significant Bit
bit(n) bit(n+1) bit(N-2)
bit(N-1)
MSB=Most…
Perchè abbiamo studiato il DAC se ci serve un
ADC ?
• L’ ADC si costruisce dal DAC.
• Un contatore alterna all’ ingresso del DAC tutti i numeri binari
possibili (da 0 a 2N-1) . Dal DAC esce quindi una rampa di
corrente crescente al crescere del numero.
• Un comparatore confronta la corrente in uscita dal DAC con la
corrente da misurare: quando sono uguali il contatore viene
fermato: il numero binario a cui è arrivato è la rappresentazione
binaria della corrente in ingresso.
• Questo numero può essere trasferito al visualizzatore o al
computer per immagazzinarlo.
• Nella scheda audio di un normale computer ci sono 2 ADC (è
stereo) che fanno questo lavoro di campionatura dei segnali
musicali 44100 volte al secondo, con risoluzione di 16 bit.
ADC dal DAC
MSB
io
Contatore:
parte da 0
e arriva
a 2N-1
DAC
LSB
Ferma il contatore
quando diventa alto
i
Comparatore:
diventa alto
quando i diventa
maggiore di io
ADC dal DAC
+
MSB 2N-1
clock
Fa partire il
contatore
-
Contatore:
parte da 0
e arriva
a 2N-1
Amplificatore
Differenziale
io Ad alta Ri
DAC
LSB 20
Ferma il contatore
quando diventa alto
i
Comparatore:
diventa alto
quando i diventa
maggiore di io
Il multimetro digitale
• Contiene al suo interno
tutta l’ elettronica di cui
sopra.
• Comunque non è uno
strumento perfetto !
• Leggere il manuale per
capire sensibilità e
precisione.
Dal Manuale del multimetro
digitale Fluke 77 (v. pag. web)
manuale multimetro digitale Fluke 77 …
Manuale Fluke 77
Misure di resistenza: Metodo Voltamperometrico
• Il modo più banale di misurare una resistenza è
quello di misurare la differenza di potenziale V
ai suoi capi e la corrente I che ci scorre. Poi si
usa la legge di Ohm: Rx =V/I.
• Avendo a disposizione due strumenti di misura,
si può eseguire la misura in due modi:
RV
Rx
Modo A
RV
RA
RA
Rx
Modo B
Misure di resistenza: Metodo Voltamperometrico
• Nel modo A la ddp misurata è proprio quella ai
capi di Rx, ma la corrente misurata è la somma di
quella in Rx e di quella nel voltmetro.
• Nel modo B la corrente misurata è proprio quella
attraverso Rx , ma la ddp è la somma di quella ai
capi di Rx e della caduta sull’ amperometro.
RV
IV
Ix
VV
IA
Rx
Modo A
RV
Vx
RA
Rx
Modo B
RA
VA
Misure di resistenza: Metodo Voltamperometrico
I A  IV  I x
IA  Ix
RV IV  Rx I x
VV  I x ( Rx  RA )
1
 Ix  IA
Rx
1
RV
1
 Vx  VV
RA
1
Rx
VV
 Rx 
IA
RV
 Rx 
1  
 RV 
IV
Ix
VX VV 1
 Rx 

I X I A 1  RA
Rx
VV
IA
Rx
Modo A
; V x  I x Rx
RV
Vx
RA
Rx
Modo B
RA
VA
Misure di resistenza: Metodo Voltamperometrico
VV
Rx 
IA
VV 1
Rx 
I A 1  RA
Rx
 Rx 
1  
 RV 
• Quindi in ambedue i casi il rapporto di tensione e corrente
misurate è una prima approssimazione del valore della resistenza.
• Nel modo A la misura è tanto più precisa quanto RV>Rx.
• Nel modo B la misura è tanto più precisa quanto più RA<Rx
RV
IV
Ix
VV
IA
Rx
Modo A
RV
Vx
RA
Rx
Modo B
RA
VA
Misure di resistenza: Metodo Voltamperometrico
• Se si ha a disposizione un solo multimetro, si eseguono
sequenzialmente la misura di corrente e quella di
tensione.
RV
RA
Rx
Misura 1
Misura 2
Rx
• La resistenza sarà inserita in un circuito che ci fa
scorrere corrente:
+
+
V
-

Rx
-
RA
+
V
-

Rx
-
RV
Misure di resistenza: Metodo Voltamperometrico
+
+
V
-

Rx
-
RA
+
V
-

Rx
RV
-
• Nella prima configurazione la corrente che scorre nell’
amperometro è uguale a quella che scorre nella resistenza; nel
secondo caso la ddp misurata dal voltmetro è uguale a quella ai
capi della resistenza (ma la corrente nella Rx è diversa da
prima..)
Misure di resistenza: Metodo Voltamperometrico
+
+
V
-

Rx
RA
-
+
V
-

Rx
RV
-
• Possiamo schematizzare il circuito esterno al multimetro secondo
Thevenin: Vo =V, Ro =+Rx
;
R’o=//Rx , V’o =VRx/(+Rx)
+
+
Vo
-
Ro
+
RA
-
circuito equivalente
+
V’o
-
R’o
RV
-
circuito equivalente
Misure di resistenza: Metodo Voltamperometrico
• Possiamo schematizzare il circuito esterno al multimetro secondo
;
R’o=//Rx , V’o =VRx/(+Rx)
Thevenin: Vo =V, Ro =+Rx
+
+
Vo
-
Ro
+
+
V’o
-
IA=IR RA
-
circuito equivalente
R’o
RV
-
circuito equivalente VV=VR
• La tensione e la corrente misurate nei due casi sono quindi:
IX
V0
V



  RX  RA
R0  R A
VX
 VR X
RV
V
 
'
RV  R 0
   RX
'
0
V

  RA
R X  1 
RX


RV
 
  R V   // R X




  .......

Misure di resistenza: Metodo Voltamperometrico
IX 
VX
V0
V


  RX  RA
R0  R A
 VR X
 
   RX

RV
 
  R V   // R X
V

  RA
R X  1 
RX





  .......

   RA 
1

RX 

   RA  RX 
RV
VX

  RX


 RX 1
IX
RX    RX  RV   // RX 
   
1 


1 1
 RX  RV 1  / RX 
Quindi all’ ordine 0:
R
(0)
X
VX

IX
Misure di resistenza: Metodo Voltamperometrico
   RA 
1

RX 

   RA  RX 
RV
VX

  RX


 RX 1
IX
RX    RX  RV   // RX 
   
1 


1 1
 RX  RV 1  / RX 
Quindi all’ ordine 0:
E all’ ordine 1:
RX(1)
R
(0)
X
VX

IX


1
 


1  ( 0 ) 1 
(0) 
RX  RV 1   / RX 
(0) 
 RX
   RA 
1 

(0) 
RX 

Misure di Resistenza: ponte di Wheatstone
A
Ro
+
V
-
R4
R3
R
B
R1
D
R2
• Trovare che condizione
devono soddisfare le
resistenze R1,R2,R3,R4
perchè in R non scorra
corrente (ponte in
equilibrio)
• Si risolve direttamente:
VB  VD
I
R
VB  VD  VB  VC  VD  VC 
I1 R1  I 2 R2 ma, essendo I  0
C
VC  VA
VC  VA
I1 
e I2 
R1  R4
R2  R3
 R1 R3  R2 R4
Misure di Resistenza: ponte di Wheatstone
A
Ro
+
V
-
R4
A
R
B
R1
R3
D
R2
C
C
• Una soluzione più furba consiste
nel ridisegnare il ponte così:
come due partitori in parallelo.
• Allora perchè in B ci sia la
stessa tensione che in D basta
che i due partitori abbiano la
stessa partizione, cioè che
R1
R2

R1  R4 R2  R3
ovvero
R1 R3  R2 R4
Misure di resistenza, altro utilizzo in lab. del
ponte di Wheatstone
Compact Pirani Gauge Sensor, Range 10-4 Torr, KF16 NW16, PN PTR26950A
Misure di Resistenza: Ohmmetro
Ohmetro
A
RA
+ V
-
V
I
RA  Rx
Rx
V
 Rx   RA
I
• è uno strumento tarato con cui si
eseguono misure di resistenza in
modo semplice e rapido, anche
se con sensibilità e precisione
modeste.
• è costituito da una batteria con in
serie un milliamperometro. Si
misura la corrente che circola
quando il circuito è chiuso sulla
resistenza incognita.
• La scala è graduata in modo che
ci si legga direttamente la
resistenza Rx
• è una scala fortemente non
lineare.
Misure di Resistenza: Ohmmetro
• Questo circuito non consente di variare la sensibilità dello strumento
nè di compensare variazioni di tensione della batteria.
– R=resistenza che permette di variare la portata; f=f.e.m. batteria
– R1=resistenza interna amperometro
– R2=resistenza addizionale di shunt, variabile (>>RA) per compensare la scarica
della batteria
Ohmetro di base
Ohmetro reale
R1
A
A
RA
+ V
-
A
Rx
R2
+
Rx
f
-
R
Misure di Resistenza: Ohmmetro
• La corrente I che passa nell’ amperometro vale
R2
f
R2
f


IA  I
R2  R1 R  R  R2 R1 R2  R1 ( R  Rx )(1  R1 / R2 )  R1
x
R2  R1
• Quindi l’ andamento di IA(Rx)
è iperbolico inverso: la
R1
A
corrente aumenta al diminuire
della resistenza incognita.
A
• Si fissano f,R,R1,R2 in modo
R2
che I(Rx =0)=IFS.
+
Rx
f
f
I A(Rx  0)  IFS 
R(1 R1 / R2 )  R1
R
Rx  
Rx  0
Regolazione
Meccanica
Rx  
R2
Rx  0
Misure di Resistenza: Ohmmetro
• La natura non lineare dello strumento rende molto imprecisa la
misura per Rx grande. Da:
f
IA 
( R  Rx )(1  R1 / R2 )  R1
usando I FS
f

R(1  R1 / R2 )  R1
si può ricavare Rx in funzione di IA e poi differenziare rispetto a
IA: si ottiene:
Rx
Rx
IA
IA

IA
1
I FS
 
se I
A
 0 e se
I
A
 I
• Si conclude che l’ errore relativo diverge ai due estremi della
scala. Si deve quindi scegliere sempre un fondo scala che porti l’
indice entro +il 30% della metà della scala.
FS
Come si minimizzano le
incertezze in misure di resistenza
• Minimizzando variazioni di temperatura
delle R stesse (R(T)=R0(1T))
basse correnti che scorrono nel resistore
(eff. Joule)
• Effetti resistenza dei contatti (specialmente
per piccole R) in serie...
• Effetto resistenze parassite (umidità,
pulizia contatti, caso R elevate) in
parallelo...
Come si minimizzano le
incertezze in misure di resistenza
• Contributo non trascurabile (in alcune
condizioni) dei cavi!
Lettura a 4 fili!
Lettura a 2 fili
+
Rfilo
V
I
RX
-
VV  VRX  2 IR filo
Rfilo
è la tensione che si misura con il voltmetro....e se Rfilo
è grande rispetto a RX ne dobbiamo tener conto....
Qui I e’ nota perche’ e’ quella fornita dal generatore di corrente
Lettura a 4 fili
+
V
Rfilo
I
RX
Rfilo
VV  VRX  2 IR filo
Tensione misurata dal Voltmetro, ma in questo caso....I=0!!!
I e’ sempre quella di prima, fornita dal generatore di corrente, e RV
è alta ... (I nella maglia del Voltmetro è zero!)